基于有限元法的吊钩结构研究

韦铁平， 曾寿金， 练国富

(福建工程学院 机械与汽车工程系, 福建 福州 350118)

基于有限元法的吊钩结构研究

韦铁平， 曾寿金， 练国富

(福建工程学院 机械与汽车工程系, 福建 福州 350118)

钢索起吊重物的摆动角度是影响吊钩结构强度的重要因素。通过有限元软件ANSYS模拟计算，揭示吊钩结构的危险截面及钢索摆动角度对吊钩结构强度的影响规律。计算结果表明：吊钩结构的危险截面分别在A-A、B-B和C-C截面处；随着摆动角度的增大，水平附加分力引起的A-A和C-C截面处的应力值变化极小，而B-B截面呈递增趋势，影响显著。分析结果为吊钩结构的强度设计提供理论依据。

起重机； 吊钩； 摆角； 有限元法

吊钩是起重机械中重要构件，是直接承受物重载荷的部分。起重机吊钩如果发生断裂或损坏，将会造成重大的安全事故。为保证起重机械安全稳定运行，起重机吊钩的结构及工况参数的选择非常重要。Toshihisa等[1]对船用吊钩进行静力学分析及疲劳试验，发现圆弧过渡角的改变对吊钩强度的影响不大，但柄部直径的大小对吊钩强度影响明显。T. Muromakia等[2]认为吊钩设计具有类似典型的锥形为最佳形状。Y. Torres等[3]发现吊钩的断裂是由应变时效脆化造成的。K. Easterling[4]指出可通过预测应力的集中区域，优化起重机吊钩的形状，延长其工作寿命并降低故障率。此外，通过数值模拟分析，可揭示吊钩结构应力、应变分布规律，并确定吊钩的危险截面[5-9]。上述研究主要针对吊钩结构参数对其强度的影响分析，而运行工况中吊物钢索与吊钩之间的摆角变化同样对吊钩安全工况造成影响。

本研究以量程为32 t的起重吊钩作为研究对象[10]，对吊钩变化摆角的工况模型进行数值模拟计算，从而确定吊钩结构的危险截面并探讨摆角对吊钩强度的影响规律，为吊钩结构的强度设计提供理论依据。

1 吊钩的有限元模型

1.1 吊钩模型简化

选择的吊钩为M级强度、材料为Q345qD，结构如图1。Q345qD是低合金高强度结构钢，具备较高的强度、韧性，能够承受机车车辆的载荷以及冲击，有较好的抗疲劳性、低温韧性和耐大气的腐蚀性。

(a)整体示意图 (b)A-A截面 (c)C-C截面 图1 吊钩结构尺寸示意图(单位：mm)Fig.1 The dimension of hook structure(unit:mm)

吊钩结构的强度为研究重点，直杆螺纹作为约束端，螺纹可简化。采用大型前处理软件ANSA对复杂模型建立有限元网格模型，吊钩结构的有限元模型如图2。单元类型选择Solid185，节点数为20 693个，单元数为10 479个。

图2 吊钩结构有限元模型Fig.2 The finite element model of hook structure

1.2 边界条件及加载

1.2.1 边界条件

吊钩和吊钩梁通过螺纹连接。为研究吊物过程钢索摆角对吊钩结构的影响，在此处吊钩的螺纹面上施加全自由度约束不会造成太大误差[9]。

1.2.2 加载

1.3 强度理论

第三强度理论认为，使材料发生塑性屈服的主要因素是最大切应力τmax，无论材料处于何种应力状态，只要构件中的最大切应力达到某一极限切应力值τu时，就会引起材料的塑性屈服。考虑安全因数，此理论的强度条件为：

(1)

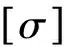
该理论的缺陷是没有考虑中间主应力σ2的影响。

第四强度理论认为，使材料发生塑性屈服主要取决于畸变能密度。即无论材料处于何种应力状态，只要其畸变能密度到达某一极限值时，就会引起材料的塑性屈服。此理论的强度条件为：

(2)

其中，σ2为主平面对应的主应力；σ1≥σ2≥σ3。

拉伸试验证明，对于钢材、铝、铜等塑性材料而言，第四强度理论比第三强度理论更符合试验结果。本文将采用第四强度理论作为吊钩结构破坏评判准则。

2 模拟结果与分析讨论

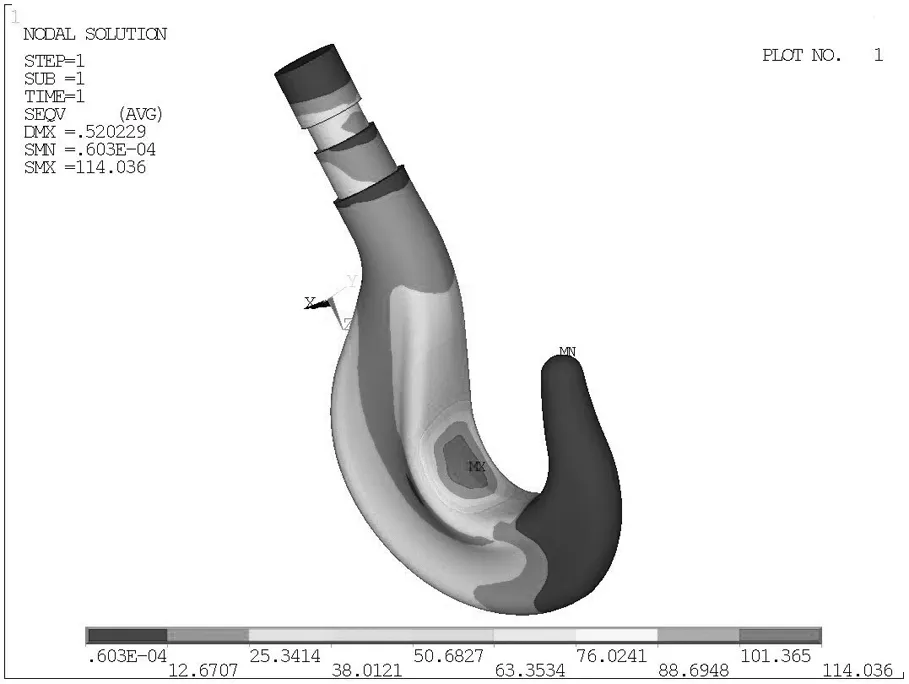
(a)=-30°

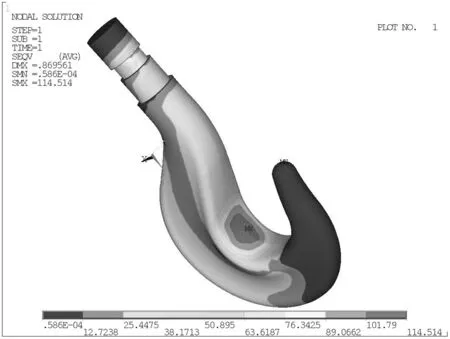
(b)=0°

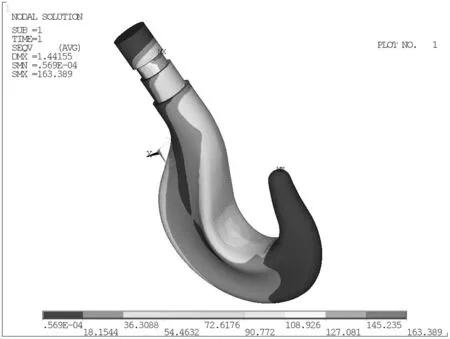
(c)=30°图3 不同摆角位置下吊钩结构的应力云图Fig.3 The stress cloud diagram of hook structure under different swinging angles

分析结果选择第四强度理论计算Von Misses 应力显示云图分布。图3(a)、(b)和(c)分别为钢索摆角为-30°、0°和30°吊钩结构的应力云图。图中显示，吊钩结构的集中应力发生在A-A截面、B-B直杆螺纹和C-C截面处，吊钩危险截面随着摆角的改变会发生变化。由图3(c)可知，吊钩在-30°～30°之间的载荷作用下，最大Von Misses应力数值不超过164 MPa，吊钩材料满足强度要求。

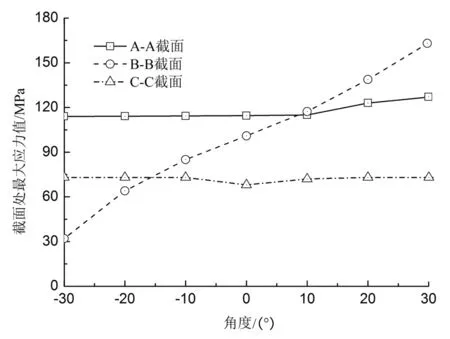
图4 摆角对各截面处集中应力值的影响规律Fig.4 The effect of the concentrative stress on the sections of hook structure

(a)A-A截面附加载荷 (b)吊钩直杆轴线E的变形图5 外载对吊钩结构的影响分析Fig.5 The influence of lifting weight on the sections of hook structure

1)图4显示，C-C截面处仅受竖直方向吊物G作用，钢索摆角引起的水平分力F对C-C截面不会造成影响。因此，该截面处最大应力值不会受到钢索摆角影响。

3 结论

1)不同工况下，吊钩结构可能的危险截面为A-A、B-B和C-C。吊物钢索摆动，水平方向会产生附加分力。摆角越大，水平附加分力越大，而竖直分力恒为吊物重量。

2)水平分力会在B-B和A-A截面产生附加弯矩，A-A和B-B截面处的应力为竖直分力产生的应力值与附加弯矩产生的应力值的叠加。摆角为负值时，A-A截面应力值基本不受影响；摆角为正值时，A-A截面应力值缓慢增加。而对于B-B截面，随着摆角的增大，其拉应力值单调递增且变化极大。

3)从数值模拟分析结果看，各种工作状态下的吊钩结构强度仍然充裕。因此，在满足强度要求的基础上，吊钩结构可做进一步优化。

[1] Nishioka T, Lee H, Won Y, et al. Strength evaluation of marine crane hooks by static-load and fatigue experiments[J]. Ocean Engineering， 2010,45(Special):1027-1032.

[2] Muromaki T, Hanahara K, Nishimura T, et al. Multi-objective shape design of crane-hook taking account of practical requirement[C]//Proceedings of the 2nd International Symposium on Computational Mechanics and the 12th International Conference on the Enhancement and Promotion of Computational Methods in Engineering and Science.Hong Kong-Macau China. Nov.30- Dec.3,2009. Washington D C:AIP Publishing,2010,1233(1):632-637.

[3] Torres Y, Gallardo J M, Dominguez J. Brittle fracture of a crane hook[J]. Engineering Failure Analysis,2010,17(1):38-47.

[4] Shaban M, Mohamed M I, Abuelezz A E, et al. Determination of stress distribution in crane hook by caustic[J]. Stress,2013,2(5):369-370.

[5] 高海峰,白广忱,费成巍.起重机吊钩等效应力非线性可靠性灵敏度分析[J].机械设计与制造,2014(6):167-170.

[6] 闫兴民,张亮有.基于SolidWorks起重机吊钩的有限元分析[J].机械工程与自动化, 2016(1):44-45.

[7] Easterling K. Introduction to the Physical Metallurgy of Welding[M]. Berlin:Elsevier,2013.

[8] 卢泽晖,胡吉全.基于ANSYS的起重机吊钩有限元分析[J].装备制造技术,2011(2):44-46.

[9] 李水水,李向东,范元勋,等.基于ANSYS的起重机吊钩优化设计[J].机械设计与制造,2012(4):37-38.

(责任编辑： 陈雯)

Study of hook structure based on finite element method

Wei Tieping, Zeng Shoujin, Lian Guofu

(College of Mechanical and Automotive Engineering, Fujian University of Technology, Fuzhou 350118, China)

The swinging angle of a steel cable is a key factor affecting the strength of hook structure. The brittle sections of the hook structure and the law of the swinging angle affecting the strength of the hook structure were revealed with ANSYS software. The results indicate that the sections of A-A, B-B and C-C are the brittle sections. The tensile stress of the sections of A-A and C-C changes very little, but rises markedly in the section of B-B with the increase of the swing angle. The results can serve as a theoretical basis for the strength design of crane hook structure.

crane; hook; swinging angle; finite element method

10.3969/j.issn.1672-4348.2017.03.007

2016-12-01;

2016-03-20

福建省属高校科研专项(JK2014032)；福建省青年自然科学基金项目(2017J05071)；福建省自然科学基金项目(2015J01181)

韦铁平(1984-)，男(壮族)，广西贵港人，讲师，博士，研究方向：强度设计、力值计量。

TB121；O346

A

1672-4348(2017)03-0234-04