引导探究分析，提高学习能力

林良勇

摘 要：在课程改革背景下，从课本的一道例题出发，对探究性教学理念在实践中的应用的教学尝试.引导学生进行探究，通过类比圆上任意一点与任意一条直径两个端点的斜率之积为定值（点不在直径上）的这个性质，进一步探究分析得到椭圆、双曲线也有该性质，通过分析比较发现抛物线并没有这一性质.最后举例分析探究中所得的性质在实践中的应用.

关键词：探究性教学；圆锥曲线；斜率之积；类比归纳

引言

在教学活动中，倡导积极主动、勇于探索的学习方式，是高中新课程重要理念之一，而教师的探究性教学是该理念在课堂上的有效表现形式.探究教学应充分调动学生学习的积极性，突出学生的主体参与，让学生经历、体验、参与探究知识的发生发展过程，从而激活思维，挖掘学生的潜力，有效提高学生的数学素养.

本文以课本的一道例题为例，引导学生通过类比分析、探究，总结规律，激发学生的思维，并就探究性教学这个课题作了一点尝试，供参考.

1 案例呈现

1.1 创设问题情景

师：请大家看看这道例题：

例1：数学选修2-1（湖南教育出版社）课本76页

已知两定点A（-4，0），B（4，0），动点P使直线PA，PB的斜率的乘积为-，求证：动点P的轨迹方程为+=1（y≠0） [1 ].

1.2 组织学生活动

设P（x，y），由题设可得：·=-，整理得：+=1（y≠0），其轨迹是椭圆（不包含顶点A，B）.

做完例题，引导学生去观察、比较，深入挖掘，可能就会发现此例题隐含着圆锥曲线的一个重要性质，从而让学生体会学习数学的乐趣.

2 引导学生探究发现

师：观察±4、-与轨迹方程中的a、b之间的关系，你能给出结论与已知条件（定点坐标、斜率之积）之间的关系吗？

生：可以，椭圆方程+=1中，a2=16=42，b2=，-=-= -.

师：能否根据上面的发现，将该具体问题一般化，形成结论？

生：能，可以一般化为：

在平面上与两定点A（-a，0），B（a，0）的斜率之积为定值-（a>b）的点的轨迹为椭圆，且方程为+=1（y≠0）.

师：很棒！你能否给出证明？

生：可以，设P（x，y），由题设可得：·=-，整理得：+=1（y≠0），其轨迹是椭圆（不包含顶点A、B）.

师：该结论的必要性也成立吗？请给出证明.

生：成立！设P（x，y），由于点P在椭圆+=1上，则有y2=，所以kPA·kPB =·=-.

可概括为：

性质1：椭圆上的任意一点P与长轴的两顶点A（-a，0），B（a，0）的斜率之积为定值- .

3 引导学生类比归纳

师（启发）：由于圆可以看成特殊的椭圆，那么在圆中是否也有类似的性质？

生（举手）：圆上的点对圆的任意一直径的两个端点（该点不在直径上）的张角都为90°，此时斜率之积为-1.

学生归纳为：

性质2：圆x2+y2=r2上的任意一点P与圆的任意一条直径AB（P不在AB上）的两个端点连线，若线PA，PB的斜率存在，则它们的斜率之积为定值-1.

師（启发）：圆可以看成特殊的椭圆，圆上的点对圆的任意一条直径（点不在直径上）的张角都是90°，即斜率之积为-1.类比圆的这个特殊性，椭圆中是否也有这个性质？

经过思考、分析、类比.

生：将性质1中的A，B改为短轴顶点时也是成立的！

生（补充）：其实A，B只要是关于椭圆中心即原点对称就可以的。

师（惊喜）：能否给出证明？

生：用点差法证明，设P（x，y），A（x0，y0），B（-x0，-y0），则kPA·kPB =·=，又因为点P，A在椭圆上，则有+=1，+=1，两式相减整理得：=-，所以直线PA与PB的斜率之积为定值-.

师生共同归纳总结，性质1可改进为：

性质3：点P为椭圆+=1上的任意一点，AB为过椭圆中心的任意一条弦，若PA，PB的斜率存在，那么斜率之积为定值，且为-.

师：非常好，得到椭圆的一个重要性质，那么类比椭圆的这个性质，能否将它进一步推广到双曲线？

生齐声：可以.

学生分小组活动，经过类比、探究、分析，归纳总结为性质4.

性质4：点P为双曲线-=1上的任意一点，AB为过双曲线中心的任意一条弦，若PA，PB的斜率存在，那么斜率之积为定值，且为.

该性质的证明过程与椭圆性质的证明方法类似（略）.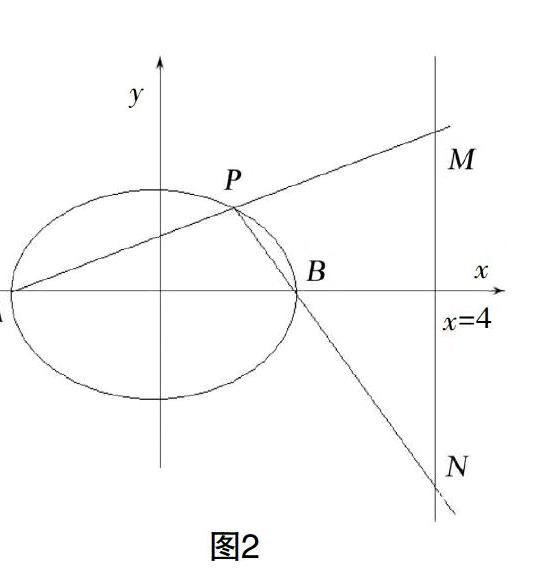

有些小组的学生自发提问：能否进一步将该性质推广到抛物线上？

学生陷入思考，共同探究分析确定：抛物线上没有该性质.原因是：圆、椭圆及双曲线都是中心对称图形，而抛物线不是，故没有.

4 灵活应用，突破难点

在解选择题、填空题时，运用此结论可以快速求解，达到小题快做、简单做的目的，同时在解决解答题时，该结论作为中间结论，用来突破难点、障碍点，也是非常有效的！

例2： 如图1，若双曲线x2-y2=a2（a>0）的左、右顶点分别为A，B，点P是第一象限内双曲线上的点，若直线PA，PB的倾斜角分别为α，β，且β=mα（m>1），那么α 的值是（ ）

A. B. C. D.

解法一：根据常规方法求解，可设P（x0，y0），则有tanα =，tanβ=，又因为x02-y02=a2，则有tanα·tanβ==1，又因为α，β∈（0，），所以α+β=，则有α=， 选D.

解法二：根据探究的结论马上有：kPA·kPB ===1，即tanα·tanβ=1，又因为α，β∈（0，），所以α+β=，则有α=，选D.

评析：常规解法以点P（x0，y0）为参变量，可求出tanα·tanβ=1，但若能利用双曲线中的这个重要性质kPA·kPB =，则答案轻松可得.

例3：如图2，已知点P为椭圆+=1上异于长轴端点 A，B的任意一点，直线PA，PB分别交直线x=4于M，N两点，以MN两点为直径做圆C.

（1）求圆C直径的最小值；

（2）圆C是否恒过两个定点？若是，求其坐标，否则说明理由.

分析一：常规解法中需设点P（s，t），求直线PA方程=直线PB方程=，再分别联立直线x=4，可得点M（4，t），N（4，t），又因为P（s，t）在椭圆上，则有t2=3-，所以MN2==，设λ=，则（12+λ）s2-96s+192-4λ=0，因为该方程有解即 Δ≥0，则λ2-36λ≥0，所以λ≥36或λ≤0（舍去），所以MN的最小值为6.

（2）略.

分析二：设M（4，m），N（4，n），不妨设m>0，n<0，

∵kPA·kPB =-=-，∴kMA·kNB =·=-，则mn=-9，∴MN=m-n=m+（-n）≥2=6，当且仅当m=3，n=-3时，等号成立.

（2）略.

评析：该题考察学生灵活应用数学知识和方法的能力，综合性较强，属于难题.如果能注意到上述探究的结论，即kPA·kPB =-=-，再灵活应用化归转化数学思想将PA，PB的斜率转化为MA，NB的斜率，就可以绕开中间参变量P的坐标，解题就显得轻松快捷，这就是这个结论在解这类难题时突破难点、障碍点的一大亮点！

应用椭圆的这个重要结论可以快速解决下面这道题的第3问，读者不妨试试.

例4：（2012年江苏高考）如图3，在平面直角坐标系 xOy中，M，N分别是椭圆+=1的顶点，过坐标原点的直线交椭圆于P，A两点，其中P在第一象限，过P作x轴的垂线，垂足为C，连接并延长AC，交椭圆于点B，设直线PA的斜率为k.

（1）、（2）略；

（3）對任意k>0，求证：PA⊥PB.

5 反思

在探究性教学中，教师应该起着“穿针引线”的作用，适时的启发、引导，积极调动学生的学习热情，突出学生的主体参与，让学生经历、 体验、探究知识的发生发展过程，让学生感受到新知识从头脑里自然的流淌出来，从而更好的培养学生学会提出问题、思考问题和解决问题的能力.学生在经历一节课的探究活动后，收获很大，应该鼓励学生课后去主动寻找类似例题，来巩固、体会、加深相关的解题思路与策略，以达到举一反三，触类旁通的效果.一节课的时间有限，后续应该对这类例题进行变式拓展，变式拓展是提升解题能力的有效途径，又可以让学生领悟新旧知识的内在联系，提高应用知识解决问题的能力.

参考文献：

[1]张景中.普通高中课程标准实验教科书 数学 选修2-1（理科）[M].长沙：湖南教育出版社，2016.