并联元件系统的延长保修定价决策优化*

● 关 磊 郝 清 张莲民

(1 北京理工大学管理与经济学院 北京 100081；2 国网冀北电力有限公司 秦皇岛 066199；3 南京大学工程管理学院 南京 210093)

并联元件系统的延长保修定价决策优化*

● 关 磊1郝 清2张莲民3

(1 北京理工大学管理与经济学院 北京 100081；2 国网冀北电力有限公司 秦皇岛 066199；3 南京大学工程管理学院 南京 210093)

在越发激烈的市场竞争中，延长保修服务已经成为企业获取竞争优势的重要渠道。本文针对存在某种并联元件的产品展开研究，考虑由一个生产商和一个零售商组成的供应链，在三种不同的模式下分析最优零售价格、延保服务价格、并联元件数量等决策。研究表明，在存在并联元件的系统里，消费者对产品质量敏感系数增加，必然会导致延保服务价格提高，并且生产商将会增加系统并联的元件数量；延保服务成本与元件质量水平的相关性越强，延保服务的价格越低，需要在系统中并联的元件数量越多。同时，对于分散决策的供应链系统，生产商更倾向于将延保服务全权授予零售商，以获得最大利润。

延保服务 并联系统 元件数量 定价决策

1.引言

伴随着社会进步与技术发展，市场上的产品越来越丰富，消费者的选择越来越多。产品的售后保修服务已经成为企业获得差异化、提升竞争力的重要途径。而近年来，产品售后保修服务已经逐渐趋于完善，基本的售后保修服务已经作为产品的一部分和产品融合在一起，所以越来越多的消费者在购买产品之后希望获得更加长久、完善的维修服务。延长保修服务(后文简称“延保服务”或“延保”)就此诞生。为了留住老顾客、吸引新顾客，企业开始将越来越多的精力放在延保服务上，并且由此形成了使消费者和企业双向受益的现实，也使得提供“以客户为中心”的个性化延保服务逐渐成为延保服务发展的一种趋势。

目前，市场上提供的延保服务主要有以下三种方式：第一种是产品的生产商直接为消费者提供延保服务，如海尔、海信等家电制造企业；第二种是生产商将延保服务全权授予零售商进行延保，这种模式在国内通常是由京东、苏宁等电商提供的延保服务；而第三种则是与产品生产商和零售商合作的第三方延保服务，典型的有新可安、美延保等。

无论哪种形式的延保服务，通常只针对一个单一而完整的产品进行分析，从而给出延保服务的定价。但是，我们所接触到的绝大多数产品都是由多个零部件组成的，零部件的质量会直接对产品的质量和维修的成本造成影响。其中，存在一类特殊的产品，这类产品中含有多个并联元件，并联元件的数量对产品的质量水平有直接影响，如手机、电脑芯片中的某些元件。本文将针对这种特殊的产品在不同的延保模式下讨论供应链中的生产商和零售商的最优决策问题，并通过数值算例的方式对结果进行深入的分析。

近年来，很多学者对延保相关的问题进行了研究。首先，一些学者讨论了不同类型的延保模式的影响。Desai等人(2004)采用Stackelberg博弈，研究了生产商协调解决其产品延保服务的制定、销售渠道问题，其研究结果表明选择双渠道的延保服务销售模式是生产商最愿意接受的、对产品生产商也是最有利的。Li等人(2012)则在Desai的基础上进行了更深入的研究，主要是进一步研究生产商或零售商销售由第三方延保服务机构提供延保服务的时候，生产商和零售商所做出的最佳决策。李铮(2013)则根据零售商两种不同的产品零售价定价策略，结合保修策略、定价策略，将零售价定价策略和保修策略进行组合。对于每种策略，作者建立了最优化模型进行分析，并求解得出生产商和零售商的最优价格策略和零售商的保修服务策略。李杰和柳键(2013)从供应链管理的角度，应用博弈论构建产品延保服务制定、销售的R模式、M模式、P3-R模式、P3-M模式4种模式最优化模型，同时引入了消费者对延保服务的需求敏感系数因素，进行研究分析，以比较不同模式下供应链成员利润及供应链系统的绩效，为供应链系统中各种角色选择相应延保服务制定、销售模式，做出最有利于自己的决策。此外，部分学者还讨论了产品质量水平与延保服务决策的相关关系。从产品角度出发，Murthy和Blischke(2005)综述了产品质量、产品保修与产品生产过程之间的相关问题。卢震和张剑(2013)则以延保服务价格和产品质量水平为决策变量，在两级供应链系统中，考虑消费者对产品质量的敏感系数、产品故障率与产品质量的相关程度两个参数变量，建立了利润最优化模型，并求解得到最优的产品延保价格和产品质量水平。聂佳佳和邓东方(2014)将产品质量水平作为内生变量，在生产商直接销售产品并提供延保服务和第三方提供延保服务两种情形下，建立了利润最优化模型并求出最优解。作者最终证明，只要提供延保服务，无论是哪种模式，其提供的产品质量水平都比没有延保服务时质量水平要高，而至于选择哪种模式提供延保服务，完全取决于何种模式下生产商的利润最大。

而对于并联元件的研究，则更多的是从质量与可靠性的角度切入，讨论对产品整体的影响。例如，钟波和孙永波(2011)用Copula函数对部件相依的并联系统进行分析，给出了Copula函数下并联系统可靠度、平均寿命和失效率的表达式，同时讨论了系统元件相关条件下的系统平均寿命和系统元件相互独立条件下系统平均寿命的关系，并且分析了并联元件数量对系统平均寿命的影响。郑铭海(2013)在并联系统开关不完全可靠的情况下，对并联系统进行状态分析，研究由n个相同部件组成的并联系统，假设修理时间服从指数分布，并进行建模分析。高文科等人(2015)则研究了在并联系统中两类故障同时存在时对维修计划和维修成本的影响，其研究表明，系统部件间的相关系数越大、更换部件的实施区间越大，系统维护成本也就越高，设备平均运行时间越短。

本文的研究借鉴了延保服务的经典文献(如Li et al., 2012)中关于不同延保服务模式的基本设定。在此基础上，本文考虑了一类存在并联元件的产品的延保服务决策问题，这是已有的研究工作都未曾涉及的，也是本文最大的创新所在。

本文后续各节的安排如下：第2节给出了模型的基本设定；第3节对三种不同模式下生产商和零售商的最优决策进行了分析；第4节结合第3节的结果进行了相应的数值计算；最后一节总结了文章的结论并讨论了未来的研究方向。

2.模型描述与符号说明

2.1 模型描述

本文针对一类最简单的并联元件系统进行研究。我们假设该并联系统有一种特定的元件，该元件的数量是可以变化的，并且元件数量的增减不会影响产品的性能，只会影响产品的质量水平或可靠性。

本文将并联系统中的元件数量作为主要的研究对象，针对图1所示的三种延保服务制定模式进行研究，分别站在生产商、零售商的角度建立最优化模型，进行求解，并进行灵敏度分析。

图1 延保服务制定的三种模式

这里，C模式指的是由生产商直接提供产品和延保服务给消费者。而R模式则由生产商将产品批发给零售商，产品及延保服务由零售商销售和提供。M模式的延保服务由生产商销售和提供，产品由零售商进行销售。

2.2 符号说明

后文中涉及的主要数学符号的含义如下：

a：产品市场容量；

b：消费者对产品价格的敏感系数；

q：产品系统部件质量水平；

w：产品批发价格；

p：产品单位价格；

c：产品单位生产成本；

pe：产品单位延保价格；

n：并联元件数量；

c0：单个元件的成本；

ce：延保服务的单位成本；

ke：质量成本参数；

d：消费者对产品质量的敏感系数；

η：维修成本与元件质量的相关程度；

γ：消费者对产品延保服务价格的敏感系数。

2.3 基本假设

对于三种不同的模式，我们假设市场需求的形式如下：

D=a-bp+dnq

(1)

其中当系统元件质量水平越高时，产品的质量水平也就越高，具有高质量的产品将会吸引更多的消费者，最终需求量将会增加。

而产品延保服务的单位成本为：

ce=ken(1-ηq)

(2)

其中当元件质量水平对维修成本的相关性η越大时，质量越好，故障率越低，维修成本降低。产品故障次数越低，产品延保服务的单位成本越低。

同时，产品的延保服务需求函数为：

De=a-bp+dnq-γpe

(3)

其中pe是延保价格。可以发现，延保需求小于产品的市场需求。

此外，本文还有如下假设：

• 维修系统元件的费用不大于购买系统元件的费用，即：nc0≥ce。

• 在R模式和M模式下，生产商和零售商形成了一个Stackelberg博弈，其中生产商是领导者，零售商是追随者。

3.模型分析与求解

3.1 C模式

在C模式下，生产商直接将产品出售给消费者，并负责为其提供延保服务。此时，生产商的决策内容包括：产品零售价格、延保价格以及并联元件的数量。

生产商通过销售产品获得的利润为：

∏1=(p-c-nc0)D=(p-c-nc0)(a-bp+dnq)

(4)

通过销售延保服务获得的利润为：

∏2=(pe-ce)De=[pe-ke(1-ηq)](a-bp+dnq-γpe)

(5)

所以，生产商的利润函数是：

(6)

(7)

(8)

证明：对生产商利润函数求一阶偏导得到：

(9)

(10)

(11)

此时，令式(9)、式(10)和式(11)分别等于0，即可得到式(7)、式(8)的结果。

证毕。

推论1：

(a)产品生产成本c越大，延保服务价格越低。

(b)产品市场容量a越大，延保服务价格越高。

产品生产成本越大，产品价格越高，产品价格升高将会导致市场上消费者对产品的需求变小，相应地，对延保服务的需求也将降低。为了一定程度上提高对延保服务的需求，生产商将通过适当降低服务价格pe来提升延保服务的需求，以获得最大的利润。

市场容量越大，消费者群体越大，购买产品及产品延保服务的数量相应地也会越大，由需求弹性理论可知，对延保服务的需求量变大，延保服务价格也将在一定范围内提高，以增加生产商的利润。

3.2 R模式

在R模式下，生产商通过零售商将产品出售给消费者，同时零售商负责提供延保服务。此时，生产商先决定并联元件的数量n和产品的批发价格w，然后，零售商再决定相应的零售价格p和延保服务价格pe。

此时，生产商的利润函数为：

∏M=(w-c-nc0)(a-bp+dnq)

零售商向消费者提供产品的利润函数为：

∏3=(p-w)(a-bp+dnq)

而零售商向消费者提供延保服务的利润为：

∏4=(pe-ce)(a-bp+dnq-γpe)

因此，零售商的利润函数是∏R=∏3+∏4。

定理2 当4γ>b时，生产商和零售商的最优解如下：

(12)

(13)

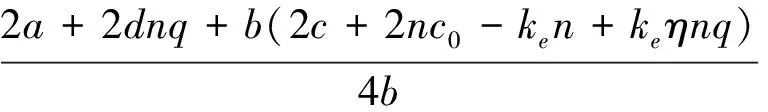
(14)

(15)

证明：首先，以延保服务价格pe、产品价格p为决策变量对零售商利润函数进行优化：

对零售商利润函数求解关于延保服务价格pe、产品价格p的一阶偏导数：

(16)

(17)

当4γ>b时，可以得到∏R关于pe和p的Hessian矩阵负定，即该利润函数关于pe和p联合凹。令一阶导数为0，即可得到式(12)和式(13)。

将得到的p*代入∏M=(w-c-nc0)(a-bp+dnq)中，以w、n为决策变量对生产商利润函数进行分析。通过求导，可以发现生产商的利润函数关于w和n不是联合凹的，所以我们先分析w，再讨论n的最优解。

此时，将由对零售商利润函数的研究得到的最优的p*代入生产商利润函数，得到生产商利润函数∏M1，以w为决策变量进行分析，可以得到：

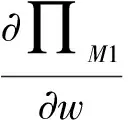
(18)

(19)

显然，生产商利润函数∏M1存在极大值。令式(18)为0，即可得到式(14)。

将得到的p*、w*代入生产商利润函数，得到新的利润函数表达形式∏M2，以系统元件数量n为决策变量进行分析，得到二阶导数如下：

证毕。

在R模式下，由于生产商和零售商分两步决策，存在4个决策变量，模型变得更加复杂。特别是对于并联元件数量的分析，只能利用其离散性特征来求解。

这里，生产商作为Stackelberg博弈的领导者，决定并联元件的数量时要在可行区间的两端进行选择，其主要的原因是：生产商此时没有零售价格和延保价格的制定权，只能通过确定并联元件数量和批发价格去影响市场。并联元件数量最少时(即n=1)，市场潜在需求较低，同时生产成本也较低，生产商通过设计合适的批发价格可以获得更高的单位利润，进而获得更高的总利润。而并联元件数量较多时，市场需求更大，尽管生产成本增加，但生产商可以通过“薄利多销”的形式获得较大的总利润。

3.3 M模式

在M模式下，生产商通过零售商将产品出售给消费者，同时，生产商为消费者提供延保服务。此时，生产商先决定批发价格、延保价格以及并联元件的数量，然后零售商再决定相应的零售价格。

此时，生产商的利润函数为：

∏M=(w-c-nc0)(a-bp+dnq)+(pe-ce)(a-bp+dnq-γpe)

而零售商的利润函数为：

∏R=(p-w)(a-bp+dnq)

(20)

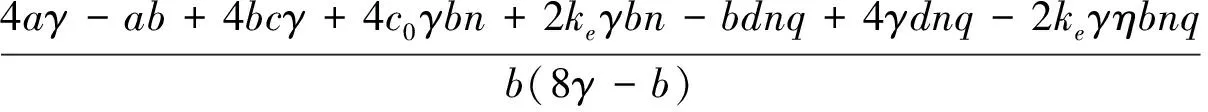
(21)

(22)

(23)

证明：首先，对零售商的利润进行求导，有：

令一阶导数为0，即可得到式(20)。

将此结果代入生产商利润函数中，可以发现此函数关于w、pe、n的Hessian矩阵不是负定矩阵。因此，将变量分开进行优化，首先以产品批发价格w、延保服务价格pe为决策变量，分析生产商利润。

此时，容易证明当4γ>b时，生产商利润函数关于w和pe的Hessian矩阵是负定的。令对应的一阶导数为0，即可解得式(21)和式(22)。

证毕。

在M模式下，仍然存在4个决策变量。此时，零售商的决策内容仅有一个零售价格，而生产商要决定并联元件数量、批发价格和延保价格三个参数。在一定的条件下，生产商的利润是并联元件数量的凹函数，因此可以求得最优的并联元件数量。

与此同时，对于供应链系统中的生产商和零售商来说，仅仅得到最优解是远远不够的。它们更加关心的是，在不同的模式下能够获得的利润是多少。进而，生产商和零售商要在这两种模式下选择更加符合自身利益的模式。

一般说来，C模式作为一种集中决策的形式，生产商能够实现的利润通常比分散决策更高。而对于R模式和M模式，在目前的模型下，我们很难直接获得生产商和零售商最优利润的表达式，也就很难对其利润进行直接比较。因此，在下一节中，我们将通过数值实验的方式对R模式和M模式下的结果进行比较分析，进而给出一些更具管理价值的结论。

4.数值算例

在本节中，我们通过数值计算的方式，对R模式和M模式下的部分结论以及生产商和零售商的利润进行分析。

具体地，根据Warranty Week(2005)以及李杰(2013)的数据及研究成果，结合本文的模型分析过程所涉及的一些不等式成立条件，数值计算中相关参数的取值如下：产品市场容量a=2000，消费者对产品的延保服务价格敏感系数γ=15，单位产品的延保服务成本ke=5，产品单位生产成本c=80，单个系统元件的成本c0=10，消费者对产品价格敏感系数b=10，产品市场价格p=100，系统元件的质量水平q=5。

4.1 R模式

在数值算例中，我们重点对生产商和零售商的几个决策以及它们所获得的利润进行分析，主要关注消费者对产品质量的敏感系数d、维修成本与系统元件质量的相关程度η的影响。

注意到，在R模式下，决定最优的并联元件数量时，要考虑两个边界条件。因此，我们首先考虑n=1时的情况。

(1)对产品零售价格p*的影响

由图3可以看出，产品的零售价格p*随着消费者对产品质量的敏感系数d的增大而提高，即市场上的消费者越关注产品质量，产品的价格越高。这与现实中消费者直观认为产品的价格反映产品质量是一致的，某种产品的价格越高，消费者认为其质量越好，对于同类产品，消费者越在意产品质量，就越倾向购买价格高的产品。

图2 产品价格p*关于d、η的三维图形

此外，也可以发现，维修成本与系统元件质量的相关程度η对产品零售价格p*没有影响。这是因为当并联元件数量确定后，零售价格与维修成本不直接相关，所以不会发生变化。

图3 延保服务价格关于d、η的三维图形

(3)对零售商最优利润的影响

从图4中，我们可以发现，零售商利润随着消费者对产品质量的敏感系数d的增大而增大，随着维修成本与系统元件质量的相关程度η的增大而增大。

图4 零售商利润函数∏R关于d、η的三维图形

(4)对生产商最优利润的影响

根据图5，生产商利润随着消费者对产品质量的敏感系数d的增大而增大，随着维修成本与系统元件质量的相关程度η的增大而增大。

图5 生产商利润函数∏M关于d、η的三维图形

小结：随着消费者对产品质量的敏感系数d的增大，产品价格p、延保价格pe提高，生产商利润和零售商的利润都随之增加。对于维修成本与系统元件质量的相关程度η，产品价格p不受其影响，延保服务价格pe随之增大而降低，生产商利润与零售商利润也随之增大而增加。

图6 生产商利润∏M关于d、η的三维图形

4.2 M模式

类似地，这里我们仍然分析消费者对产品质量的敏感系数d、维修成本与系统元件质量的相关程度η的影响。

(1)对系统中并联元件数量n*的影响。

由图7可以看出，系统中并联的元件数量n*，随着消费者对产品质量的敏感系数d的增大而先增大后减小。当d较小时，消费者对于产品质量越敏感，产品质量提升导致的产品需求量提升的幅度越大，最终会增加企业的利润，提升产品质量可以通过增加并联系统中元件数量来实现。而当d比较大的时候，需求的增加可以不再依靠并联元件数量的增加，此时减少并联元件的数量可以降低成本，增加企业的利润。

图7 系统元件数量n*关于d、η的三维图形

同时，并联元件的数量随着维修成本与系统元件质量的相关程度η的增大而增加。这是由于η变大时，改进元件质量水平将会降低产品的维修成本，企业可以通过增加系统元件数量提高产品的质量水平，增加产品和延保服务的需求量，以提高企业效益。

图8 延保服务价格关于d、η的三维图形

延保服务价格随着维修成本与系统元件质量的相关程度η的增大而提升。系统元件质量与维修成本相关程度越高，说明系统元件的质量水平对延保期间的维修活动影响越大，由于系统元件是外购的，其质量水平是外生的，质量水平过低将会导致维修成本过高，维修成本高将会导致延保服务价格提高。这与R模式下n=1时，延保服务价格与η成反比并不矛盾，因为此时并联系统中只有一个元件，其质量水平对延保服务成本的影响不会那么大。

(3)对产品零售价格p*的影响。

由图9可以发现，产品的零售价格p*随着消费者对产品质量的敏感系数d的增大而先增加后少。这主要是因为p*与并联元件数量n*线性相关，而n*随着消费者对产品质量的敏感系数d的增大也呈现先增加后少的趋势。

图9 产品价格p*关于d、η的三维图形

产品价格随着维修成本与系统元件质量的相关程度η的增大而提升，当系统元件质量水平一定时，η增大将导致延保成本相对较低，相应的延保服务价格将降低，购买延保服务的消费者数量增多，延保服务需求变大，在一定程度上也将导致消费者对产品的需求量变大，产品的需求量变大，将会导致产品价格上升。

(4)对零售商最优利润∏R的影响。

图10告诉我们零售商的利润随着消费者对产品质量的敏感系数d的增大而变大。零售商的利润随着维修成本与系统元件质量的相关程度η的变大而降低，η增大，系统元件数量增加，产品成本增加，零售商利润减少。

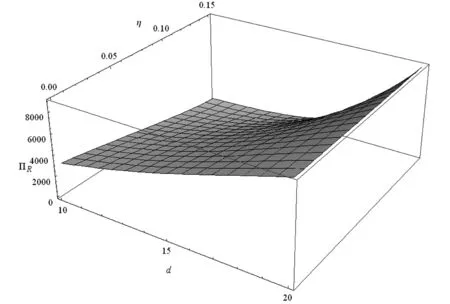
图10 零售商利润∏R关于d、η的三维图形

(5)对生产商最优利润∏M的影响。

由图11可以发现，生产商的利润∏M随着消费者对产品质量的敏感系数d的增大而增大。消费者对产品质量敏感系数越大，产品价格与延保服务价格越高，价格提高，生产商的利润也就提高了；生产商的利润∏M随着维修成本与系统元件质量的相关程度η增大而变小，但是其变化幅度不大。

图11 生产商利润∏M关于d、η的三维图形

4.3 R模式与M模式的比较

对R模式与M模式下的产品零售价格与延保服务价格进行比较，可以发现，在d、η分别取得相同的值时，M模式下的零售价格和延保服务价格均高于R模式。当延保服务由生产商提供时，零售商无法获得延保服务所带来的利润，因此会在一定范围提高产品价格以增加其利润；零售商提高产品价格将导致产品的需求量降低，为平衡或减弱产品需求量降低的影响，生产商将提高产品的延保服务价格来提高其利润。

当然，生产商、零售商最关注的还是其本身获得的利润。通过数值算例的结果可以看出，在两种模式下，当d、η分别取得相同的值时，M模式的生产商利润和零售商的利润都小于R模式下的生产商和零售商利润。因此，在分散决策供应链中，生产商更倾向于将产品的延保服务全权授予零售商来做，零售商在市场上更接近消费者，对消费者需求变化能快速做出响应，这对提高生产商利润、零售商利润都有正向的影响。

5.结论与展望

本文对于一类具有并联元件产品的延保服务问题进行了研究。考虑仅有一个生产商和一个零售商组成的供应链系统，本文在C模式、R模式和M模式三种不同情形下分析了生产商和零售商的最优决策，并通过数值算例对参数的性质进行了讨论。

通过研究，我们发现，在存在并联元件的系统里，消费者对产品质量敏感系数增加，必然会导致延保服务价格提高，并且生产商将会增加系统并联的元件；延保服务成本与元件质量水平的相关性越强，延保服务的价格越低，需要在系统中并联的元件数量越多。同时，对于分散决策的供应链系统，生产商更倾向于将延保服务全权授予给零售商来做，以获得最大利润。

本文作为一项考虑并联系统元件的延保服务决策理论研究，为继续深入探讨系统元件对延保服务的影响提供了参考。

但是本文还存在很多不足之处，对于在三种模型下求出的最优解，只是针对消费者对产品质量的敏感系数、维修成本与元件质量水平两个参数进行相关性分析，未考虑其他参数对于延保服务价格和系统元件数量的影响。同时，只存在元件并联的系统在现实生活中较少，对于延保服务策略的研究还需要针对多种更为复杂的系统来开展。未来可以在此基础上对存在串、并联的系统进行研究，还可以对存在两种或者多种不同元件组成的并联系统进行分析。此外，还可以考虑加入产品元件质量水平决策因素来建模，为延保服务理论的扩充和丰富提供更多参考。

[1]高文科, 张志胜, 刘飏, 陈霞. 故障相关的两部件并联系统可靠性建模及动态更换策略[J]. 计算机集成制造系统, 2015 (2).

[2]李杰. 供应链管理视角下产品延保服务模式选择与运营策略研究[D]. 江西财经大学, 2013.

[3]李杰, 柳键. 基于需求敏感指数的供应链延保服务模式分析[J]. 控制与决策, 2013, 28 (7).

[4]李铮. 不同零售定价策略下供应链的最优保修策略[D]. 南京大学, 2013.

[5]卢震, 张剑. 考虑质量成本的延保定价策略[J]. 东北大学学报, 2013, 34 (5).

[6]聂佳佳, 邓东方. 产品质量影响延保成本下的延保服务外包策略[J]. 工业工程与管理, 2014, 19 (3).

[7]郑铭海. 不同条件下并联系统的可靠性研究[D]. 兰州理工大学, 2013.

[8]钟波, 孙永波. 基于Copula的部件相依并联系统可靠性分析[J]. 数理统计与管理, 2011(2).

[9]Desai, P. S., Padmanabhan, P.. Durable good, extended warranty and channel coordination [J].ReviewofMarketingScience, 2004, 2 (1).

[10]Li K., Chhajed D., Mallik S.. Design of extended warranties in supply chains under additive demand [J].ProductionandOperationsManagement, 2012, 21 (4).

[11]Murthy D. N. P., Blischke W. R..Warrantyandmanagementandproductmanufacture[M]. Berlin, Germany: Springer, 2005.

[12]Warranty Week. Extended Warranty Income [EB/OL]. The newsletter for warranty management professional, http: //www.warrantyweek.com/archive/ww20051025.html. 2017-01-24.

专业主编：许明辉

Optimal Extended Warranty Pricing Strategy of Systems with Parallel Components

Guan Lei1Hao Qing2Zhang Lianmin3

(1.Management and Economics School of Beijing Institute of Technology, Beijing, 100081；2.Beidaihe Sanatorium, State Grid JIBEI Electric Power Company,Qinhuangdao,066199; 3.Management and Engineering School of Nanjing University, Nanjing，210093)

In the market with more fierce competition today, the extended warranty is one of the ways that help enterprises to gain competitive advantages. In this article, we consider a special product with parallel components. We study the optimal decisions on the retail price, the extended warranty price and the number of parallel components under three different modes with the setting of one producer and one retailer. The results show that in the systems with parallel components, the extended warranty price will increase and the number of parallel components will be larger when the sensitivity of the quality of these components increases. Meanwhile, if the relationship between the quality of the components and the warranty cost is larger, the extended warranty price will decrease, but the number of the components will be larger. At last, in a decentralized scenario, the producer will prefer that the retailer provides the extended warranty, since this will bring a larger profit for both the producer and the retailer.

Extended warranty; Parallel components; Number of components; Pricing decision

国家自然科学基金青年项目“考虑多销售方博弈的团购定价模式研究”(71401013)、“考虑时段费用的生产外包集成排序和协调机制设计研究”(71501093)，江苏省自然科学青年基金项目(BK20150566)。

张莲民，E-mail：zhanglm@nju.edu.cn

F224

A