基于模拟退火-粒子群算法优化支持向量机参数的连铸漏钢预报
方一鸣 郑贺军 刘 乐 胡春洋.燕山大学工业计算机控制工程河北省重点实验室,秦皇岛,0660042.国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004中船航海科技有限责任公司,北京,00044
基于模拟退火-粒子群算法优化支持向量机参数的连铸漏钢预报
方一鸣1,2郑贺军1刘 乐1胡春洋3
1.燕山大学工业计算机控制工程河北省重点实验室,秦皇岛,0660042.国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,0660043中船航海科技有限责任公司,北京,100044
针对连铸漏钢预报神经网络模型在小样本训练数据情况下难以获得较高预报准确率的问题,提出了一种基于模拟退火-粒子群(SA-PSO)算法优化支持向量机(SVM)参数的连铸漏钢预报算法。将粒子群优化算法引入支持向量机的训练过程中,利用其调整参数少、寻优速度快的优点,有效地提高了漏钢预报模型的寻优速度;利用模拟退火算法对粒子群算法迭代更新后粒子的新位置加以评价,来决定新位置是否被接受,避免了粒子群算法在迭代寻优过程中陷入局部极值的问题。结合某钢厂连铸现场历史数据对提出的连铸漏钢预报算法进行了测试,测试结果表明,所提算法的连铸漏钢预报准确率可达98.8%。
连铸漏钢预报;支持向量机;粒子群算法;模拟退火算法
0 引言
在钢铁生产过程中,连铸漏钢是最严重的事故之一,危及企业正常生产、人身安全及设备的寿命[1]。为了能够及时地避免漏钢事故的发生,减少企业的经济损失,很多大型钢铁企业在连铸生产中采用漏钢预报系统作出预警和处理。另一方面,在漏钢事故中黏结性漏钢事故占80%以上,因此,黏结性漏钢是连铸漏钢预报系统的主要研究对象[2]。
目前,国内外学者在漏钢预报模型方面的研究以神经网络预报模型为主[3-4]。文献[3]提出的采用变步长并加入动量项、防振荡项等方法加快神经网络收敛速度的BP神经网络漏钢预报模型,提高了神经网络训练过程中的收敛速度;文献[4]提出的基于LM(Levenberg-Marquardt)算法的BP神经网络的连铸漏钢预报算法,使神经网络在训练过程中能够跳出局部极小。文献[3]和文献[4]所提方法在一定程度上能够提高漏钢预报的准确率,但它们的网络规模大、计算比较复杂,没有解决神经网络在模型训练初期需要大量数据和泛化能力差的问题。
由于漏钢事故发生的频率小,获取到大量的训练数据是比较困难的。与神经网络相比较,支持向量机(support vector machine,SVM)在解决小样本、非线性模式识别问题中具有独特优势,可将漏钢预报问题转化成一个二次型寻优问题[5]。文献[6]提出了基于主动学习GA-SVM分类器的连铸漏钢预报方法,在训练样本有限的情况下,能够获得比较好的预测效果,避免了神经网络泛化能力差的问题。但遗传算法的交叉、变异操作复杂,需要多次迭代才能获得比较好的分类模型,寻优速度较慢。
基于上述分析,本文提出了一种基于模拟退火-粒子群算法优化SVM参数的连铸漏钢预报算法。首先,在文献[6]的基础上,建立基于SVM的连铸漏钢预报模型。然后,利用模拟退火(simulated annealing,SA)算法对粒子群优化(particle swarm optimization,PSO)算法进行改进,进而得到模拟退火-粒子群(SA-PSO)算法;该算法通过模拟退火算法对更新后粒子的适应度进行评价,进而来决定新位置是否被接受,从而避免粒子群算法的盲目调节[7-8]。与文献[6]中的遗传算法相比,SA-PSO算法在SVM的训练过程中,可避免复杂的交叉、变异操作,能够提高迭代寻优的速度[9-10]。最后,利用某钢厂连铸结晶器生产线上现场采集的数据,应用SA-PSO算法对SVM的参数进行优化并测试。
1 SVM连铸漏钢预报模型
1.1 黏结性漏钢预报原理
黏结性漏钢是造成连铸漏钢的主要原因,一般情况下,黏结性漏钢发生在弯月面处,由结晶器液面的波动或者其他某种原因导致钢水与结晶器铜板直接接触造成[11]。正常浇注情况下,坯壳沿结晶器壁向下生长,上排热电偶的温度高于下排热电偶的温度,且热电偶的温度只会在较小的范围内波动。当铸坯和结晶器壁发生黏结时,上排热电偶的温度会急剧升高,在拉坯力的作用下,黏结裂口会随着结晶器的振动向下移动。同时,在冷却作用下,上排热电偶的温度因坯壳的重新凝固弥合而下降,下排热电偶的温度开始升高,如图1所示。当上排热电偶和下排热电偶相继出现符合黏结性漏钢温度曲线时,发出预警。

图1 黏结性漏钢热电偶温度变化曲线示意图Fig. 1 Schematic diagram of thermocouple temperature change curve for bonding steel leakage
通过上文的分析可以发现:当发生黏结性漏钢时,热电偶的温度变化曲线都是先上升后下降的,所以利用热电偶测温法对连铸生产过程中可能发生的黏结性漏钢事故进行预报,主要的依据是对热电偶所检测的疑似黏结性漏钢的温度变化模式做出正确的判断,即动态波形的模式识别问题。
1.2 SVM的连铸漏钢预报模型的建立
SVM是建立在统计学习理论和结构风险最小化基础上的一种模式识别方法[12]。SVM的机理就是寻找一个满足分类要求的最优分类超平面,在保证分类精度的同时,使SVM能够实现对线性可分数据的最优分类。
假设训练样本输入为x=xi,i=1,2,…,m,对应的期望输出为y=yi∈{1,-1},yi为向量xi的类别标识。
设分类超平面H方程为
wx+b=0
(1)
式中,w为分类超平面H的法向量;b为偏置值。
为了使分类面能够对所有样本正确分类并且具备分类间隔,要求它满足如下约束:
yi(wxi+b)-1≥0
(2)
由于数据中的噪声是不可避免的,所以通过引入非负的松弛变量ξi(ξi≥0)来放松约束条件,如下式所示:
yi(wxi+b)≥1-ξi
(3)
为了解决约束最优化问题,构造Lagrange函数:

(4)
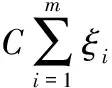
分别对w、b、ξ求偏微分,并令其等于0,可得
(5)
(6)

(7)
将式(5)~式(7)代入式(4)中得

(8)
进一步,可将式(8)的极值问题转化为
(9)
(10)
根据KKT(Karush Kuhn Tucker)条件[13],最优解应当满足:
ai[yi(wxi+b)-1+ξi]=0
(11)

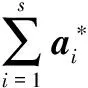
(12)
其中,x为待分类样本;b*为分类阈值,可以由任意一对支持向量取中值求得,即

(13)
对于连铸漏钢预报系统,大部分的输入样本在输入空间是线性不可分的,支持向量机为了解决非线性问题以及克服维数灾难问题,常使用核函数K(xi,xj)代替最优分类函数中的内积运算。因此,为了提高支持向量机算法的分类能力,本文选取RBF(radial basis function)核函数,RBF核函数对各种类型的数据具有良好的分类效果,其函数表达式为

(14)
式中,g为核函数系数。
因此,式(9)的极值问题可以转化为
(15)
同时,最优分类函数为
(16)
根据黏结性漏钢温度变化曲线,将热电偶的温度采样值归一化处理后作为SVM的输入。通过最优分类函数将输入的漏钢样本和正常样本进行识别,输出不同的结果,达到分类的目的。分析某钢厂连铸现场提供的漏钢数据,热电偶相邻的15个温度值可体现一次板坯的漏钢温度变化曲线,因此,选取相邻的15个温度值作为SVM的输入向量xi,xi∈R15×1;下一组相邻的15个温度值作为输入向量xi+1。为了消除不同数量级的数据对SVM的影响,需要对有效数据进行归一化处理,处理方式如下:
(17)
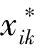
2 基于SA-PSO算法对SVM参数的优化
粒子群算法采用实数求解,需要调整的参数少、易于实现,能在较少的迭代次数内找到最优解[14]。
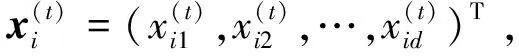
(18)
(19)
式中,r1、r2为均匀分布在(0,1)区间的随机数;c1、c2为学习因子,其取值范围为区间(1,2)。
一般将式(18)和式(19)称为标准粒子群算法。标准粒子群算法在寻优过程中存在易陷入局部极值的缺点。在粒子群迭代更新过程中引入模拟退火算法,利用其在寻优过程中的突跳能力对粒子群算法进行改进,可提高算法的全局寻优能力。
模拟退火算法是一种随机性组合优化算法,在初始温度足够高、温度下降足够慢的条件下,能够以概率1收敛到全局最优值,广泛应用于组合优化问题中。模拟退火算法以某种概率接受较差点,可以有效地避免在寻优过程陷入局部极值。
初始温度是模拟退火算法全局寻优性能的重要参数,本文采用基于适应度和接受概率的方法,初始温度T1由下式决定:
(20)
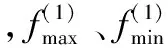
将训练样本等分为10组,其中9组样本代入式(15)所示的SVM分类器模型,求出每个训练样本对应的ai,其中非零的ai对应的训练样本为支持向量,并将所得支持向量代入式(16)所示的分类函数对第10组样本数据进行预测和验证,将预测结果与所标标签进行对比,取对比结果的准确率作为适应度值。然后,选取另外9组中任意一组作为预测和验证数据,其余9组作为训练数据重复上述过程,计算出每次的适应度值,取10次适应度值的平均值作为该10组平均适应度值。
在式(15)中,目标函数和约束条件中训练样本为已知数据,只有核参数g和惩罚因子C需要选择,并且二者对SVM模型的分类性能有显著的影响,因此需要对C和g进行寻优。本文采用SA-PSO算法对核参数g和惩罚因子C进行优化,算法的具体步骤如下:
(1)读取训练样本数据,给定惯性权重w、学习因子c1和c2,随机产生一组{C,g}作为粒子的初始位置;
(2)初始化粒子的适应度、接受概率pr,将粒子的适应度值作为个体最优极值pbest,在个体极值中选择最优值作为群体极值gbest,计算初始退火温度T1,设定最大迭代次数为100代;
(3)计算粒子的适应度fi(k)和平均适应度favgi(k)。若粒子的适应度值优于原有个体极值pbest,则将当前适应度值设置为pbest,选择最优的个体极值作为群体极值gbest;
(4)判断算法是否达到设定的最大迭代次数?若是,则输出结果;否则,进行k从1到K的循环部分,其中K为设定的最大迭代次数;
(5)根据式(18)、式(19)更新各粒子的飞行位置和速度;
(6)计算新粒子的适应度fi(k+1)、平均适应度favgi(k+1)和适应度的变化量Δf=fi(k+1)-fi(k)。若Δf<0或exp(-Δf/Tk)>rand,则接受新位置;否则,保留旧位置;
(7)退火操作:Tk+1=θTk,其中θ∈(0,1),本文取θ=0.7,转步骤(3)。
3 基于SA-PSO优化SVM参数的连铸漏
钢预报模型的训练与测试
通过对某钢厂现场采集的历史数据进行分析,挑选出60组样本作为SVM连铸漏钢预报模型的训练样本,其中包含30组正常样本和30组黏结性漏钢样本。进一步,为了测试SVM连铸漏钢预报模型的泛化能力,测试样本和训练样本应避免重复和交叉,从现场采集的历史数据中筛选出195组测试样本(其中包括85组黏结性漏钢样本、100组正常样本和10组伪黏结漏钢样本),用来对SVM连铸漏钢预报模型进行测试。
选取参数c1=1.5、c2=1.7。基于SA-PSO算法的SVM模型经过训练后,惩罚因子C为0.01,核函数参数的值为51.9916。
网络模型的测试性能指标为:预报准确率ηp和报出率ηr,它们的表达式为
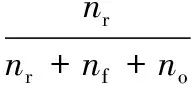
(21)

(22)
式中,nr为正确报警次数;nf为错误报警次数;no为漏报次数。
利用训练好的标准PSO-SVM模型和SA-PSO-SVM模型分别对195组测试样本进行分类,分类效果如图2和图3所示。标准PSO-SVM模型有5次误报,SA-PSO-SVM模型仅有1次误报。
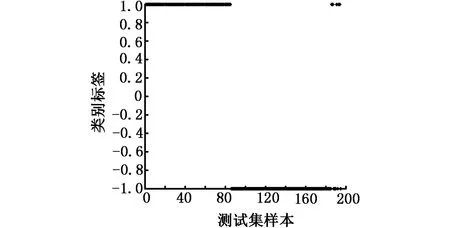
图2 标准PSO-SVM模型分类效果图Fig.2 Classification diagram of standard PSO-SVM model
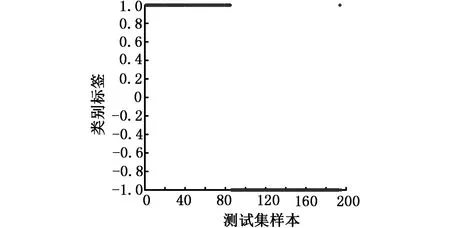
图3 SA-PSO-SVM模型分类效果图Fig.3 Classification diagram of SA-PSO-SVM model
将本文方法与文献[6]的GA-SVM方法进行对比,漏钢样本的漏报次数、误报次数和搜索到全局最优值的迭代次数及根据式(21)和式(22)计算出三种模型的预报准确率和报出率如表1所示。

表1 模型的预报性能
从表1中可以看出:GA-SVM模型、标准PSO-SVM模型和SA-PSO-SVM模型对黏结性漏钢样本全部报出,可以达到100%的漏钢报出率。在相同训练样本和测试样本条件下,三种模型对漏钢样本和正常样本分类正确,但对离分类面比较近的伪黏结性漏钢样本进行分类时,标准PSO-SVM模型误报次数为5次,GA-SVM模型误报次数为2次,SA-PSO-SVM模型将误报次数降低为1次,SA-PSO-SVM模型对伪黏结性漏钢样本具有更好的识别能力。此外,钢铁企业采用连铸漏钢预报系统的目的是避免漏钢事故的发生,因此,连铸漏钢预报模型的预报速度是一项重要指标。SA-PSO-SVM算法在迭代过程寻找全局最优值方面,比GA-SVM算法耗时短,缩短了寻优所需要的时间,提高了漏钢预报模型对漏钢事故的预报速度,能够及时地避免漏钢事故的发生。
4 结论
本文提出的基于模拟退火-粒子群算法优化SVM参数的连铸漏钢预报方法,采用在解决小样本、非线性模式识别中具有优势的支持向量机作为连铸漏钢预报的模型,解决了神经网络训练初期需要大量漏钢数据进行训练的缺点及泛化能力差的问题。粒子群算法对SVM的参数进行优化时,调整的参数少,寻优速度快,提高了模型的预报速度。将模拟退火算法引入到粒子群算法寻优过程中,借助模拟退火算法对更新后的粒子的新位置进行评价,来决定新位置是否被接受,避免了粒子群算法在寻优过程中陷入局部极值。根据仿真结果可知,基于SA-PSO算法优化SVM参数的连铸漏钢预报系统的预报准确率达到98.8%,对伪黏结性漏钢样本具有较高的识别能力,降低了连铸漏钢预报模型的误报率。
[1] 王唯一, 荣亦诚, 龚幼民, 等. 连铸漏钢诊断预报技术的研究[J]. 机电一体化, 2000,6(4):60-65. WANG Weiyi, RONG Yicheng, GONG Youmin, et al. Techniques for Breakout Diagnostic Prediction in Continuous Casting Process[J]. Mechatronics,2000,6(4):60-65.
[2] 刘永贞, 王旭东, 贾启忠, 等. 结晶器内黏结漏钢及其传播行为的研究[J]. 炼钢, 2009,25(3):45-48. LIU Yongzhen, WANG Xudong, JIA Qizhong, et al. Investigation in the Behavior of Sticking Breakout and Its Propagation in Slab Continuous Casting Mould[J]. Steelmaking,2009,25(3):45-48.
[3] 厉英, 王正, 敖志广, 等. BP神经网络漏钢预测系统优化[J]. 控制与决策,2010,25(3):453-456. LI Ying, WANG Zheng, AO Zhiguang, et al. Optimization for Breakout Prediction System of BP Neural Network[J]. Control and Decision,2010,25(3):453-456.
[4] 张本国, 李强, 王葛, 等. 基于改进BP神经网络的连铸漏钢预报[J]. 中国机械工程,2012,23(2):204-207. ZHANG Benguo, LI Qiang, WANG Ge, et al. Breakout Prediction Based on Improved BP Neural Network in Continuous Casting Process[J]. China Mechanical Engineering,2012,23(2):204-207.
[5] DSA V. Advanced Support Vector Machines and Kernel Methods[J]. Neurocomputing,2003, 55(1/2):5-20.
[6] 方一鸣, 胡春洋, 刘乐, 等. 基于主动学习GA-SVM分类器的连铸漏钢预报[J]. 中国机械工程,2016,27(12):1609-1614. FANG Yiming, HU Chunyang, LIU Le, et al. Breakout Prediction Classifier for Continuous Casting based on Active Learning GA-SVM[J]. China Mechanical Engineering,2016,27(12):1609-1614.
[7] 高鹰, 谢胜利. 基于模拟退火的粒子群优化算法[J]. 计算机工程与应用,2004,40(1):47-50. GAO Ying, XIE Shengli. Particle Swarm Optimization Algorithms Based on Simulated Annealing[J]. Computer Engineering and Applications,2004,40(1):47-50.
[8] 刘爱军, 杨育, 李斐,等. 混沌模拟退火粒子群优化算法研究及应用[J]. 浙江大学学报: 工学版,2013,47(10):1722-1730. LIU Aijun, YANG Yu, LI Fei, et al. Chaotic Simulated Annealing Particle Swarm Optimization Algorithm Research and its Application[J]. Journal of Zhejiang University(Engineering Science),2013,47(10):1722-1730.
[9] EBERHART R, KENNEDY J. A New Optimizer Using Particle Swarm Theory[C]// Proceedings of the 6th International Symposium on Micro Machine and Human Science. NewYork:IEEE,1995:39-43.
[10] 邵信光, 杨慧中, 陈刚. 基于粒子群优化算法的支持向量机参数选择及其应用[J]. 控制理论与应用,2006,23(5):740-743. SHAO Xinguang, YANG Huizhong, CHEN Gang. Parameters Selection and Application of Support Vector Machines Based on Particle Swarm Optimization Algorithm[J]. Control Theory and Applications,2006,23(5):740-743.
[11] 李同彬, 姚若华, 陈波. 几种常用漏钢预报系统模型的比较[J]. 冶金自动化,2009,33(4):1-4. LI Tongbin, YAO Ruohua, CHEN Bo. Comparison of Useful Breakout Prediction System Models[J]. Metallurgical Industry Automation,2009,33(4):1-4.
[12] SMOLA A J, SCHÖLKOPF B. A Tutorial on Support Vector Regression[J]. Statistics & Computing, 2004,14(3):199-222.
[13] 曹建, 孙世宇, 段修生, 等. 基于KKT条件的SVM增量学习算法[J].火力与指挥控制, 2014, 39(7): 139-143. CAO Jian, SUN Shiyu, DUAN Xiusheng, et al. SVM Incremental Learning Algorithm Based on KKT Conditions[J]. Fire Control & Command Control,2014,39(7):139-143.
[14] KENNEDY J, EBERHART R. Particle Swarm Optimization[C]// IEEE International Conference on Neural Networks, 1995. New York: IEEE, 1995:1942-1948.
(编辑 王艳丽)
Breakout Prediction for Continuous Casting Based on SA-PSO to Optimize Parameters of SVM
FANG Yiming1,2ZHENG Hejun1LIU Le1HU Chunyang3
1.Key Labof Industrial Computer Control Engineering of Hebei Province,Yanshan University, Qinhuangdao,Hebei,066004 2.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling,Qinhuangdao,Hebei,066004 3.CSSC Marine Technology Co.,Ltd.,Beijing,100044
In order to overcome the problems that the neural network model was difficult to obtain a high accurate breakout prediction for continuous casting under the conditions of small sample training data, a breakout prediction for continuous casting was proposed based on SA-PSO algorithm to optimize the parameters of SVM. Firstly, the PSO algorithm was introduced into the training processes of SVM, increasing the optimization speeds of breakout prediction model by using the advantages of less parameters and fast optimization speeds. Secondly, SA algorithm was used to evaluate the new positions of updated particles, and to determine whether the new positions were accepted, which could avoid the PSO algorithm steped into the local extremum in optimization processes. Finally, the breakout prediction for continuous casting was tested by the history data of continuous casting. The results show that the proposed algorithm may make the breakout prediction accuracy reach 98.8%.
breakout prediction for continuous casting; support vector machine (SVM); particle swarm optimization(PSO) algorithm; simulated annealing(SA) algorithm.
2016-07-27
国家自然科学基金委员会与宝钢集团有限公司联合资助项目(U1260203);国家自然科学基金资助项目(61403332);河北省高等学校科学技术研究青年基金资助项目(QN2016122);河北省高等学校创新团队领军人才培育计划资助项目(LJRC013)
TF345
10.3969/j.issn.1004-132X.2017.12.012
方一鸣,男,1965年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为冶金自动化系统,系统集成和计算机控制,复杂系统建模仿真和控制,自适应、鲁棒控制理论与应用。获国家科技进步二等奖2项。发表论文170余篇。E-mail:fyming@ysu.edu.com。郑贺军,男,1989年生。燕山大学电气工程学院硕士研究生。刘 乐,男,1985年生。燕山大学电气工程学院讲师。胡春洋,男,1988年生。中船航海科技有限责任公司系统集成设计工程师。

