复杂载荷作用下压气机叶片疲劳寿命数值分析
张俊红 刘 萌 付 曦 寇海军 林建生天津大学内燃机燃烧学国家重点实验室,天津,300072
复杂载荷作用下压气机叶片疲劳寿命数值分析
张俊红 刘 萌 付 曦 寇海军 林建生
天津大学内燃机燃烧学国家重点实验室,天津,300072
为提高叶片服役寿命,在计算叶片应力分布并预测其在复杂载荷作用下的疲劳寿命后,基于逆向工程建立了三种不同精度的叶片模型;考虑离心和气动载荷作用,求解压气机叶片复合载荷作用下的应力分布规律;通过叶片模拟件疲劳试验,确定TC4钛合金疲劳极限,拟合寿命模型参数;利用非线性连续损伤力学模型预测叶片在典型工况下的疲劳寿命。结果表明:不同模型的应力及寿命计算值存在一定差异,开展叶片数值分析时,需考虑计算模型还原叶片几何特征的精度对计算结果的影响。
航空发动机;压气机叶片;逆向建模;复杂载荷;疲劳寿命
0 引言
压气机叶片压缩空气为燃烧室提供高压气源,长期运行在高速、高压、高温的环境中,随着发动机转速和压比的不断提高,叶片的服役环境愈发恶劣,因此准确预测叶片疲劳寿命、提高叶片运行可靠性是保证发动机正常运转的关键[1]。
目前,叶片疲劳寿命预测主要通过疲劳试验和数值研究开展。疲劳试验能准确反映结构的疲劳特性,但成本相对较高;采用数值方法模拟结构的损伤行为,既易于操作又可重复实现,在降低寿命预测研究成本的同时,也可为疲劳试验提供理论依据[2]。开展叶片疲劳数值研究,需建立叶片实体模型,考虑到航空发动机叶片曲面造型复杂[3],在无法获取结构设计参数的前提下,利用正向设计方法建立叶片模型存在困难。为克服这一难点,研究人员将逆向工程[4]应用于叶片三维造型,准确快速地重构叶片几何形状。随着逆向建模技术日趋成熟,叶片逆向模型的曲面特征更为精确,可有效描述结构的疲劳行为,为叶片疲劳寿命的数值研究提供较为可靠的数值模型。
作为提高空气压力的转动部件,引发压气机叶片疲劳失效的载荷种类较多,包括叶片旋转产生的离心载荷、空气流动产生的气动载荷和由此激发的叶片振动载荷,以及温度分布不均引起的热负荷等。一般认为,压气机位于燃烧室前端,可忽略温度影响,因此离心、气动载荷是造成压气机叶片疲劳失效的主要载荷因素[5-7]。采用计算流体力学方法获取叶片表面气动参数,可准确计算叶片在复杂载荷作用下的应力分布[8-10],确定疲劳失效危险点,结合损伤力学合理选择疲劳模型,即可预测叶片实际工况下的疲劳寿命。
关于疲劳寿命模型,通常采用N-S曲线法[6,11],该模型参数易拟合,满足工程计算,但不能体现应力比、平均应力等载荷参数的影响,因此,人们将连续度概念引入疲劳研究[12]。CHABOCHE等[13]根据连续损伤力学推导的非线性连续损伤模型具有较高的计算精度。疲劳模型中包含的材料参数通常需要结合疲劳试验数据进行拟合,以保证获得准确的模型参数,同时可以根据疲劳试验验证预测模型计算结果的准确性,提高模型计算精度。
本文基于逆向工程建立叶片实体模型。由于叶片型面复杂的扭曲特性,描述叶片几何形状的点云数据繁多,在不影响逆向叶片扭转特性的前提下,适当简化曲面拟合控制条件,是保证逆向造型拟真度、降低建模复杂性的关键[5],因此,本研究提出三种逆向建模方案,简化拟合曲面的型面截线,结合计算流体力学获取叶片在离心、气动等复杂载荷作用下的应力分布,确定叶片危险位置的最大应力,利用Chaboche模型预测逆向叶片的疲劳寿命。
1 物理模型
1.1 计算流体力学基本方程
计算流体力学通过求解流体控制方程来预测流体运动规律,流体控制方程包括连续性方程、N-S方程和能量守恒方程。连续性方程表示为
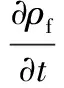
(1)
式中,t为时间;ρf为流体密度;v为流体速度矢量。
N-S方程表示为

(2)
式中,ff为体积力矢量;p为流体压力;μ为动力黏度。
对于包含热交换的流动系统,其能量守恒方程为

(3)
式中,T为流体温度;λ为流体热导率;cp为质量定压热容;ST代表黏性耗散项。
考虑流场与结构场的相互作用,在耦合交界面处需满足以下方程:
(4)
式中,n为方向矢量;τ为应力;df为流体位移;ds为固体位移。
1.2 疲劳寿命预测方法
连续损伤力学基于连续介质的热力学理论研究结构的损伤演化行为,考虑损伤累积过程中材料力学性能退化对疲劳失效行为的影响,将结构的疲劳寿命看作是损伤变量连续累积直至破坏发生的一个完整过程。
CHABOCHE等[13]基于连续损伤理论,提出了一个描述损伤变量D与载荷参数σ非线性关系的损伤累积方程,其微分表达式为
dD=f(D,σ)dN
(5)
式中,N为寿命循环数。
该方程认为加载参数与损伤变量具有不可分离性,当外载为应力时,Chaboche模型表达式如下:
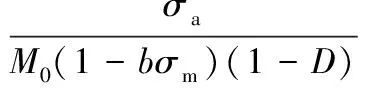
(6)
其中,β、M0、b为材料参数;σm为平均应力;σa为应力幅;α是与载荷、损伤都相关的参数,α表达式为

(7)
σ1(σm)=σm+σl0(1-bσm)
(8)
其中,符号〈〉定义为:当x≤0时,〈x〉=0;当x>0,〈x〉=x。σmax为循环载荷最大应力;σl0为对称加载下的材料疲劳极限;σu为材料抗拉强度;H、α为方程相关参数,可根据疲劳试验结果求得。
当结构未出现损伤时,D=0;疲劳破坏发生时,D=1。将式(6)从D=0到D=1积分,可以得到结构疲劳寿命表达式:

(9)
2 叶片计算模型
2.1 逆向建模方案设计
叶片为某型航空发动机高压压气机五级动叶(图1a),叶身高154.8 mm,初始扭转角33.4°。初始扭转角使叶身曲面特征复杂,逆向建模时曲面拟合精度在很大程度上影响叶片的弯曲及扭转特性,使应力及寿命的计算结果存在差异。为探求逆向建模方法对数值计算的影响,本文提出三种逆向叶片建模方案:沿叶展方向分别构造4条、6条、10条型面截线,以进排气边轮廓线及叶身型面截线作为限制条件,重构叶身曲面(下文分别称为B4模型、B6模型、B10模型)。采用光学高速测量系统对叶片表面及轮廓进行三维扫描,将点云数据导入三维造型软件,经过提取、精简及平滑处理后,拟合叶身曲面,得到压气机叶片三维实体模型,如图1所示。
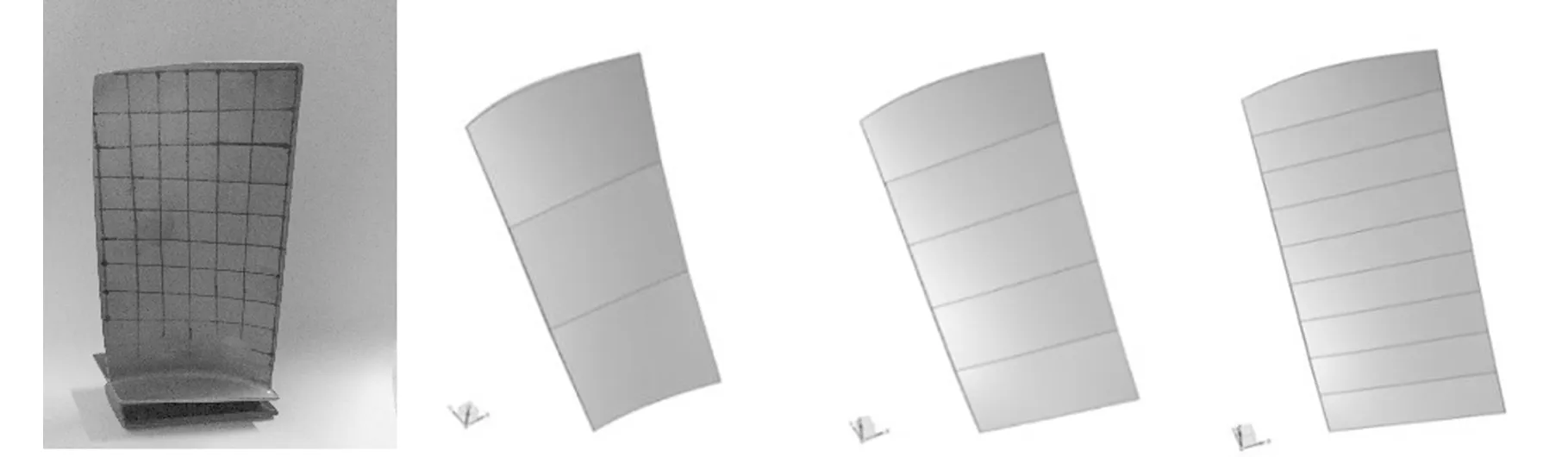
(a)叶片实物 (b)B4模型 (c)B6模型(d)B10模型图1 叶片逆向模型Fig.1 Reverse blade model
2.2 叶片有限元模型
采用十节点四面体单元对叶片三维模型进行网格划分,建立三种逆向叶片的有限元模型,网格单元数分别为302 048、321 470、317 218。叶片三种有限元模型的网格单元数处于同一量级,消除了有限元网格划分对计算结果精度的影响。考虑实际工作过程中,叶片与轮盘采用燕尾榫方式进行装配,对叶片榫头与榫槽接触的表面施加法向约束、榫头前后施加轴向约束。压气机叶片材料为TC4钛合金,弹性模量E=107 GPa,密度ρ=4440 kg/m3,泊松比υ=0.34,抗拉强度σu=1005 MPa[14]。
2.3 叶片有限元模型验证
叶片逆向建模时,重构曲面需进行一定简化,造成逆向叶片与实物存在误差,通过对比实际叶片固有频率的试验值与模拟仿真的计算值,进行逆向叶片拟真度的校核。
图2所示为叶片模态试验现场。叶片固定于试验台上,LMS振动测试系统连接加速度传感器和压电式力传感器,通过单点激励、单点响应的方法测试叶片的固有频率和模态振型。压力传感器实时记录激励力,激光测振仪作为加速度传感器,通过非接触式测量获取叶片激励作用下的动态响应,将采集的信号传入测试系统进行数据处理与分析。叶片模态试验与有限元模拟结果如表1所示,三种逆向模型前6阶固有频率的有限元计算结果与试验结果的相对误差均在10%以内,保证了逆向叶片的建模精度,满足后续分析需要。

图2 叶片模态试验Fig.2 Modal test of blade
对比表1前6阶模态的计算值与试验值,发现B4模型模态频率的计算误差相对较大,B10模型在低阶的模态频率计算值较准确,3、4、6阶的相对误差均大于其他两个模型。对比模态频率计算值的误差变化规律,发现B6、B10模型均具有较小的误差波动,且B6模型的计算结果与B10的计算结果较为接近。B6模型在保证模态计算结果较准确的同时有效降低了建模的复杂性,而B10模型具有更准确的模态计算结果,但建模过程相对最为复杂。
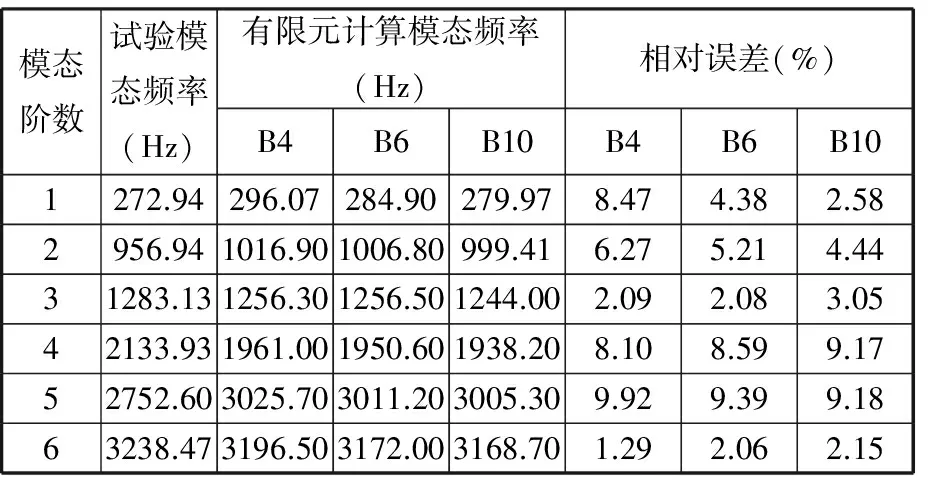
表1 叶片试验模态与计算模态频率对比
3 典型工况及载荷分析
3.1 典型工况
本文基于发动机试车数据,将该发动机的完整工作循环简化为起飞、中间、最大连续、巡航和慢车5个典型工作状态,如表2所示。统计航空发动机1000飞行小时的功率区间数据[15],得到功率状态分配谱(表3)。在确定发动机5个典型工作状态的基础上,将发动机的工作过程简化为0-起飞-0、慢车-中间-慢车、0-最大连续-0、巡航-最大连续-巡航、慢车-最大连续-慢车5个工作循环,每种循环的转速示意图见图3,相应的发动机1000飞行小时转速循环压缩谱如表4所示。

表2 发动机典型工作状态

表3 发动机功率状态分配谱(1000 h)[15]
3.2 载荷分析及流场模型
发动机运转过程中,叶片主要受自身旋转产生的离心载荷、气体流动产生的气动载荷以及由此引起的振动载荷影响。叶片在离心和气动载荷复合作用下发生振动,会产生复杂的应力状态,这往往是造成叶片振动疲劳失效的主因。鉴于此,本研究同时考虑离心载荷和气动载荷的作用,进行叶片应力分布计算及疲劳寿命预测。

(a)0-起飞-0(b)慢车-中间-慢车
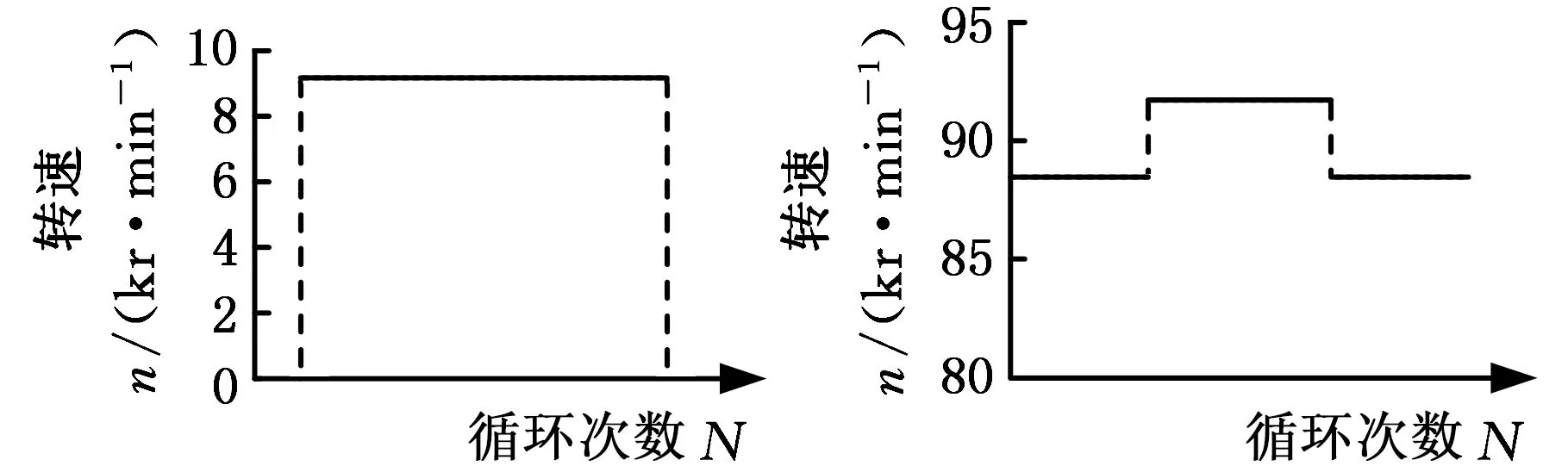
(c)0-最大连续-0(d)巡航-最大连续-巡航

(e)慢车-最大连续-慢车图3 典型工作循环转速示意图Fig.3 Speed diagram of typical working conditions

表4 发动机1000飞行小时转速循环压缩谱[15]
为了解叶片流动特性,计算不同转速下叶片表面承受的气动载荷,分别以三个叶片逆向模型为基础建立流场模型。根据该航空发动机维修手册,设置叶尖间隙为1.7 mm,并添加进出口流道,以减小进出口边界压力波反射对流场计算域的影响。以6条型面截线的叶片模型为例,其流场模型和流场网格模型如图4所示,三种叶片模型的流场网格单元、节点数量列于表5中。

图4 叶片流场图和流场网格图Fig.4 Flow field model of blade

表5 叶片流场网格单元、节点数
利用ANSYS Fluent软件对典型工况下的压气机叶片表面压力及应力分布进行数值模拟。计算流场处于湍流状态,选择k-ε湍流模型和标准壁面函数,利用隐式算法和二阶迎风格式进行求解。
4 疲劳模型参数拟合
4.1 叶片模拟件疲劳试验
疲劳试验为疲劳模型提供材料参数,是寿命预测数值研究的基础。本研究使用叶片模拟件进行疲劳试验,在保证相似性的基础上,降低试验成本。根据航空工业部标准HB5277-84[16]设计钛合金疲劳试验模拟试件,长120 mm,两侧宽20 mm,颈缩处宽10 mm,加工后试件如图5所示。

图5 疲劳试件实物图Fig.5 Test specimen
试验在室温和大气环境条件下进行。试件固定于试验台形成悬臂梁结构(图6),试验中通过试件尖端的加速度传感器测量叶尖振幅,调节加载频率及振动台加速度g值来改变试件尖端振幅。试验前标定试件尖端振幅与最大应变之间的关系(图7),将应变换算为应力。

图6 疲劳试验系统Fig.6 Fatigue test system
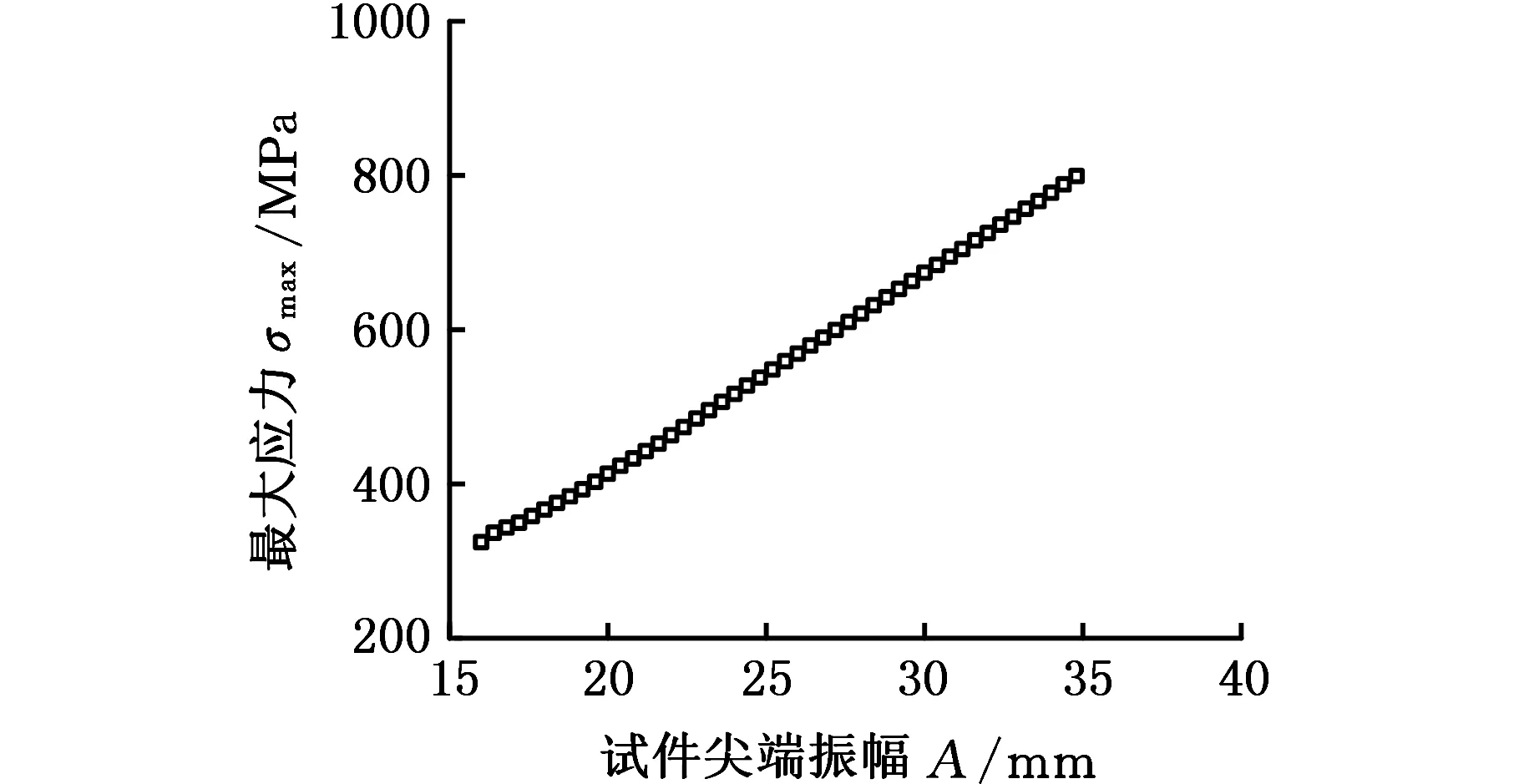
图7 试件表面最大应力和叶尖振幅标定结果Fig.7 Calibration result of maximum stress and amplitude
4.2 参数拟合
疲劳试验结果如图8所示,以达到107个循环为标准,确定TC4钛合金疲劳极限约为440 MPa。利用式(9)对试验数据进行拟合得到Chaboche模型曲线,确定材料参数H=0.139,M0=4.32×108,β=0.63,b=0.000 112,Chaboche模型表达式如下:

(10)
该模型考虑了平均应力和应力幅对疲劳寿命的影响,对于本研究中压气机叶片在不同转速工况下的复杂受力情况,利用Chaboche模型预测疲劳寿命可以表现损伤演化过程的非线性。
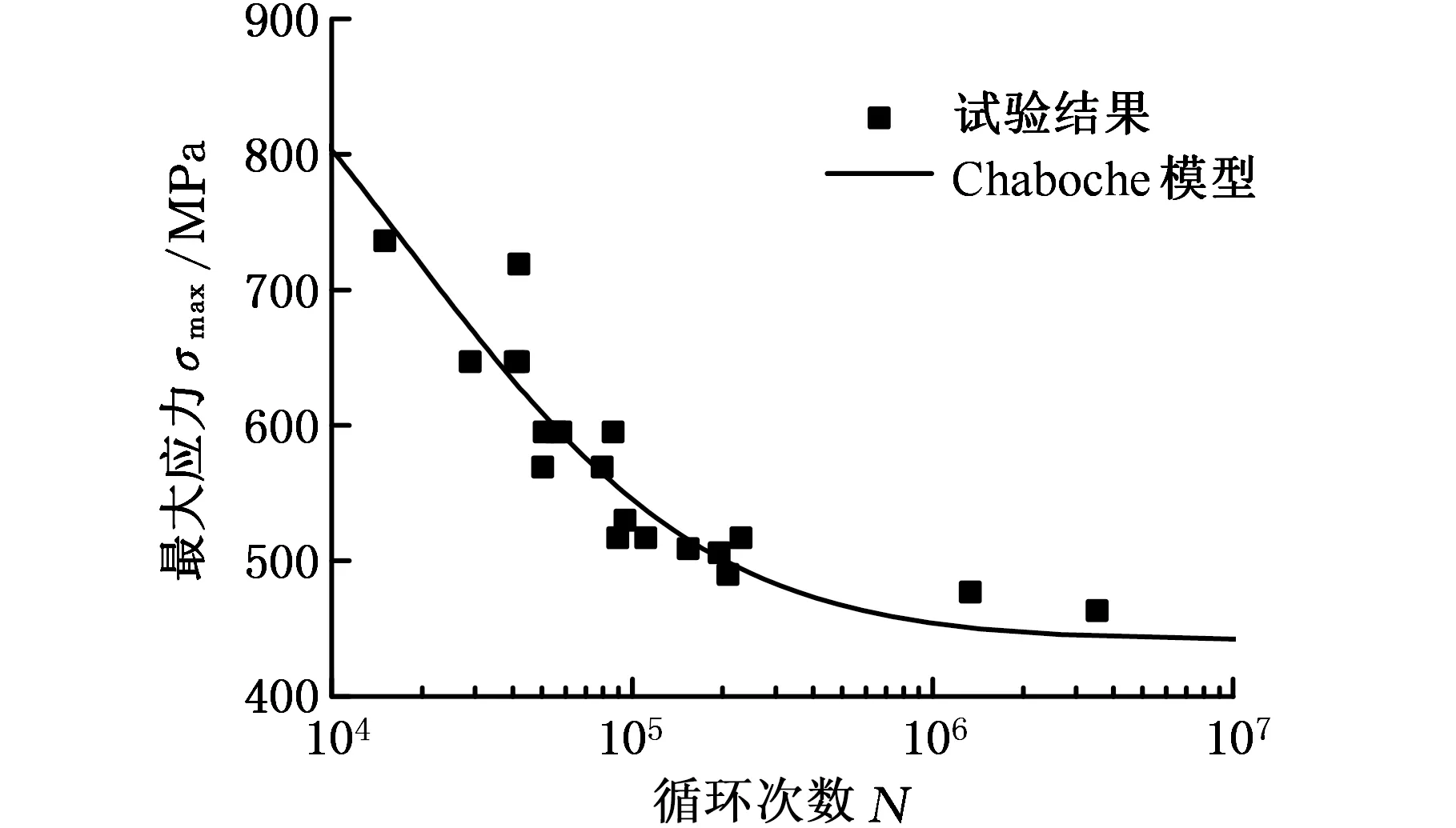
图8 TC4钛合金叶片疲劳试验结果Fig.8 Fatigue test results of TC4 blade
5 数值计算与分析
5.1 应力分布
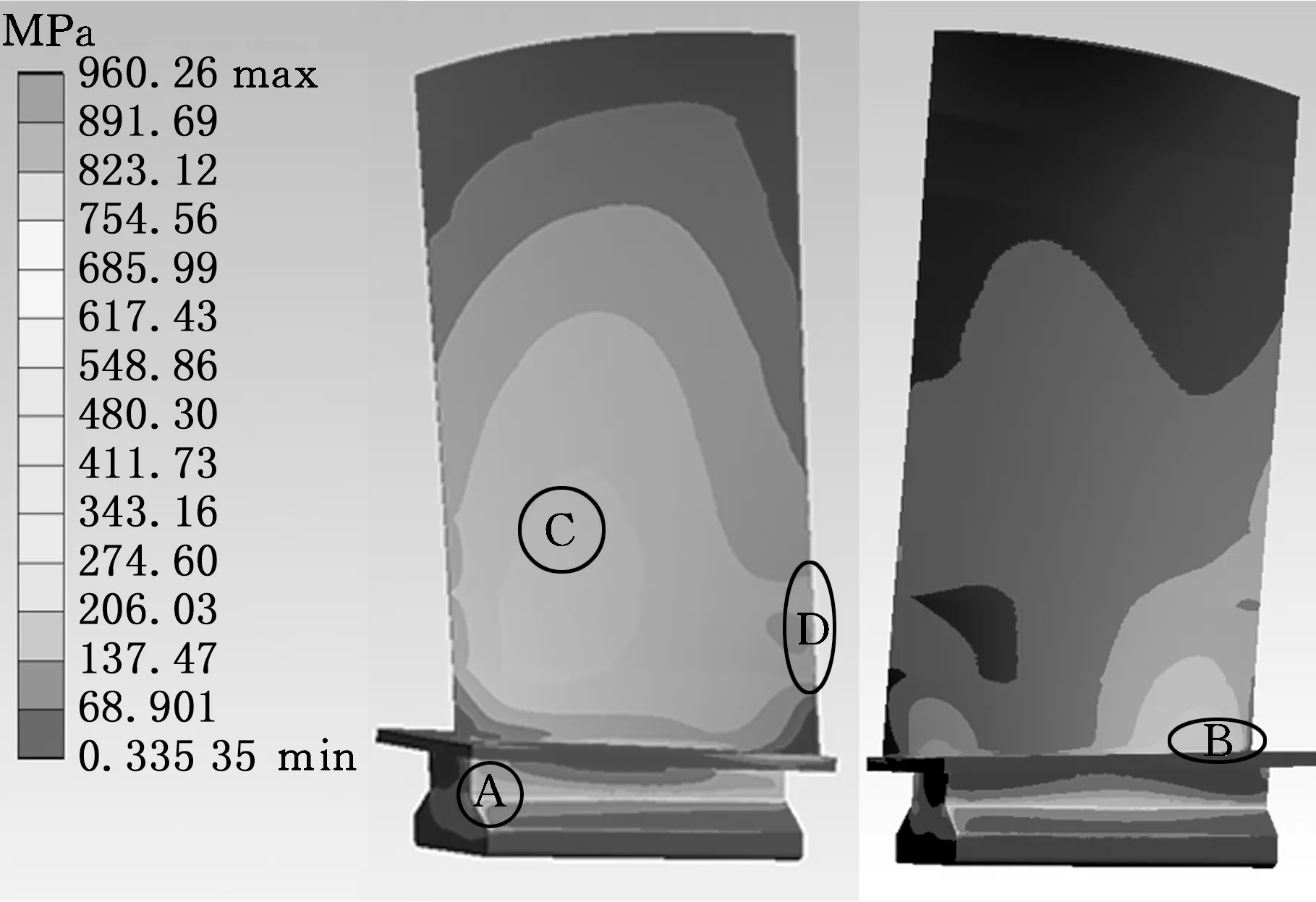
图9 叶片应力分布及应力集中区域Fig.9 Stress distribution of blade
叶片在不同转速工况下受离心、气动载荷作用时的等效应力分布规律相似,以起飞工况为例进行分析,如图9所示,应力集中区域主要包括:榫头排气端面A处、叶背面叶根B处、叶盆面叶身中间C处以及叶盆面进气侧距叶根约30 mm的D处。叶盆面应力分布趋势为:C处应力较大,应力值向四周逐渐降低,且沿叶尖方向应力降幅较大,因此叶尖的应力值最小,应力主要集中在C处。叶背面应力分布趋势为:B处应力最大,应力值沿叶展方向逐渐降低,叶尖的应力值最小,应力主要集中在叶片根部。所建立的三个叶片模型,在不同转速工况下叶片应力分布趋势基本相同,但应力值有所区别。进一步对比三个模型在区域A、B、C、D的最大应力随转速的变化规律,探讨建模方案对叶片应力分布的影响。
如图10所示,三种叶片模型在区域A、B、C、D的最大应力随转速的变化趋势均为随转速增大而增大,但区域A应力增大的速率较区域B、C、D更快。研究认为,当转速越高,叶片在离心、气动载荷作用下产生的应力越大,更易导致叶片在危险位置发生疲劳失效。准确获取叶片在较高转速工况下的应力分布,可以保证叶片的疲劳寿命预测值更加精确。
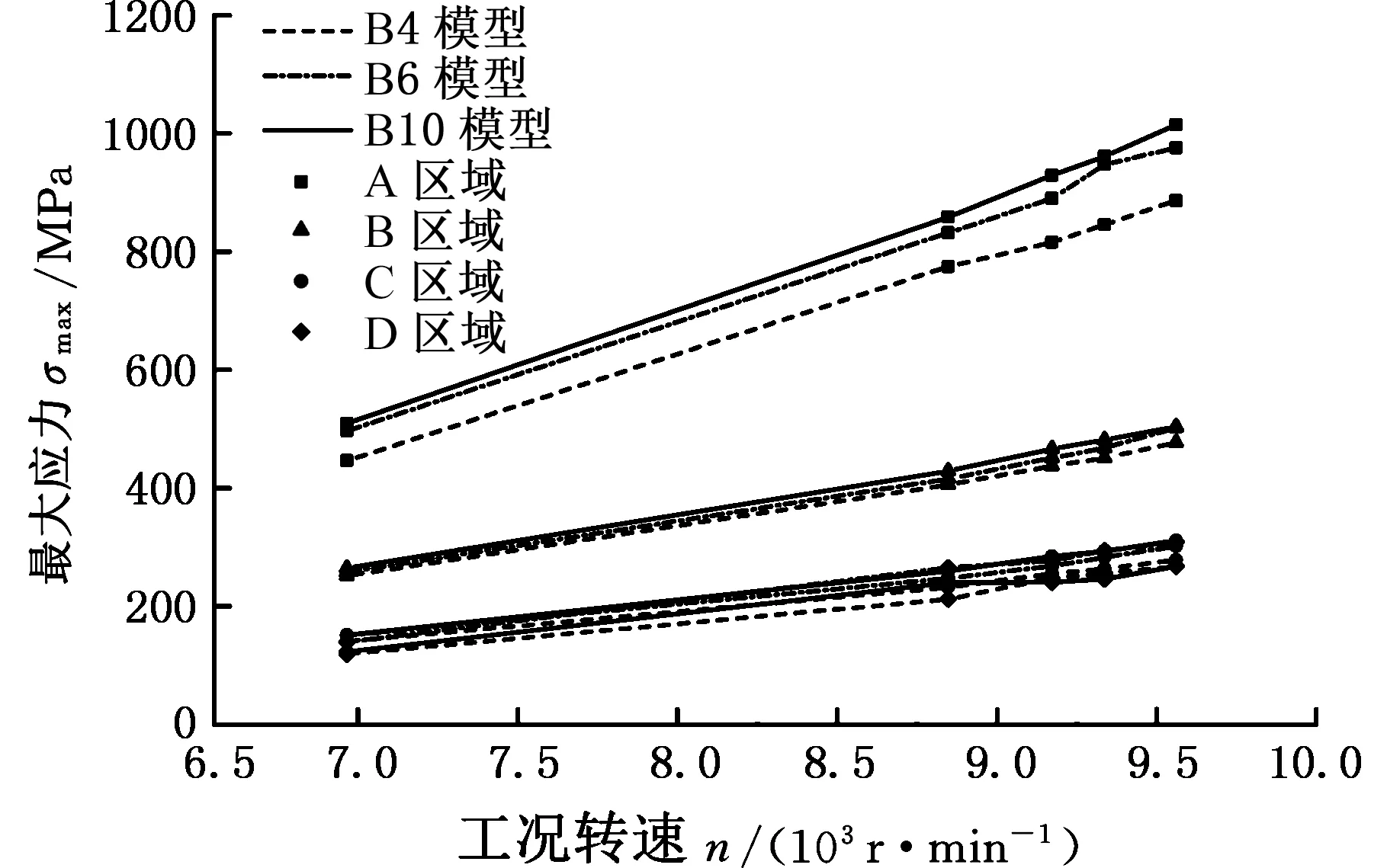
图10 最大应力随转速变化曲线Fig.10 Maximum stress of blade under different rotate speed
进一步分析图10、图11曲线发现,不同应力集中区域在相同转速下出现最大应力所对应的叶片模型不唯一,因此可以认为叶片建模方式对应力分布计算结果有影响,下面分别分析三种叶片模型在四个危险区域的最大应力值的变化规律。

(a)区域C
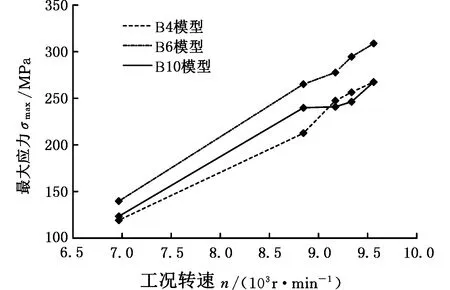
(b)区域D图11 不同叶片模型C、D区域最大应力随转速变化曲线Fig.11 Maximum stress of Area C and D under different rotate speed for different blade model
榫头排气端面A、叶背面叶根B和叶盆面叶身中间C三个区域的最大应力值在任何转速工况条件下均表现为:B4模型应力计算值最小、B10模型应力计算值最大,B6模型的计算值介于B4、B10之间,且与B10计算值较为接近。对比相同转速区间,三个模型在相同危险区域的最大应力值随转速的增长率基本一致。但与区域A、B、C不同的是,区域D的最大应力计算值在不同叶片模型和不同工况转速条件下的变化趋势较为复杂。B4、B6、B10三个模型D处最大应力分别位于距叶根46 mm、35 mm、29 mm处,应力计算值随转速的变化规律虽然都表现为递增关系,但相同转速区间不同叶片模型应力的增长速率存在差异。由图11b可以看出,B6和B10模型D处应力随转速的变化规律较为一致,应力增长率表现为先减小后增大;而B4模型恰好相反,最大应力的增长率为先增大后减小。上述分析说明,B4模型的计算结果较其他两种模型存在误差,而B6与B10模型的计算精度较为一致。
综合分析三个模型的计算结果,认为造成上述应力分布规律变化的原因为:B10模型拟合点云数据的型面截线数较多,扭转叶片曲面重构精度更高,受到的扭转应力更大,因此,区域A、B、C均表现为B10模型的应力计算值最大。对于危险区域D,B10模型D处最大应力点较B4、B6模型更靠近叶根,这是由于扭转叶片的流场特性发生变化,叶片在气动载荷作用下受弯扭复合应力的作用,导致其最大应力点向叶根移动。比较B4、B6和B10三个模型,B10模型更好地还原了叶片的扭转特性,但不能忽略其建模过程复杂的缺点;B6模型在简化建模的基础上,保证应力分布规律与B10模型基本一致,且应力计算差值较小;B4模型则存在较大计算误差。后续研究将根据疲劳寿命的计算值进一步说明建模方案对寿命预测造成的影响。
在进行疲劳寿命研究时,理论上应选择叶片受力较大的区域A作为危险位置。但A处的最大应力值明显高于B、C、D三处,结合上述分析,造成A处应力集中的原因可能包括叶片榫头建模不精确以及固支边界条件与实际情况不完全相符。本研究旨在分析叶身应力分布情况及预测疲劳寿命,建模时简化榫槽造型,并忽略榫槽、轮盘与榫头的接触及受力情况。鉴于此,以区域A作为危险位置预测叶片疲劳寿命并不准确,本文将叶背面叶根处B区域确定为危险位置,进行后续疲劳寿命研究。
5.2 寿命预测
根据叶片在离心、气动载荷作用下的应力分布计算结果及上述应力变化规律的分析,以叶背面叶根处B区域的最大应力点作为预测疲劳寿命的危险点,参考发动机典型循环工况,编制叶片载荷谱(表6),得到不同工况下叶片疲劳寿命预测值(表7)。

表6 危险点载荷谱

表7 叶片各工作状态及完整循环疲劳寿命
对比表7中寿命数据可知,在起飞、中间、最大连续和慢车四个工况中,不同叶片模型的疲劳寿命计算值由大到小的顺序均为:B4、B6、B10。在巡航工况,则是B6模型的寿命计算值最大,B10模型最小,B4模型的计算值介于中间。这与区域B的最大应力点在相应工况下应力值变化规律不一致,其原因主要为,叶片在危险位置的疲劳寿命不只与该点的应力有关,还与该工况下叶片所受载荷的应力比相关。因此在巡航工况,B4模型的应力计算值最小,其疲劳寿命却略低于B6模型的结果。
根据表3给出的发动机功率状态分配谱,计算该发动机高压五级叶片的疲劳寿命,设起飞工况、中间工况、最大连续工况、最大巡航工况、慢车工况的疲劳寿命分别为N1、N2、N3、N4、N5,则计算公式为:1.64%N1+2.13%N2+18.83%N3+31.62%N4+45.78%N5,结果列于表7最后一列。
结果表明,本文所建立的三种逆向叶片模型,其寿命均达到19 000飞行小时,符合104飞行小时的标准,但计算值有所不同。分析发现,对于同一叶片,不同的建模方案重构叶片曲面特征的精度不同,导致应力分布和疲劳寿命计算值有所差异。对比表7三种模型完整循环的疲劳寿命,虽然差值较小,但B10模型具有更大的安全系数。综合模态频率及应力分布的结果,可以认为B10模型的计算精度最高,同时建模过程也最为复杂;而B6模型则在保证计算准确的基础上,降低了建模的难度;B4模型建模方法最简单,但计算误差也相对较大。因此,研究认为采用数值方法开展相关计算时,应考虑建模方法对计算精度造成的影响,尤其对于包括空间曲面的复杂结构,需在简化建模方法的基础上,保证模型的拟真度,提高数值计算的准确性。
6 结论
(1)本文基于逆向建模理论拟合点云数据,建立了三种曲面拟合精度不同的叶片模型。利用计算流体力学,分析压气机叶片在离心与气动载荷作用下的应力分布规律,结合疲劳试验,开展叶片在典型工况下疲劳寿命研究。
(2)对叶片在离心、气动复杂载荷作用下的应力分布及疲劳寿命进行计算,结果表明三种叶片模型的应力分布规律相似,但应力值存在差异,从而导致寿命预测结果不同,说明采用逆向工程建立叶片模型时,不同建模方案重构几何特征的精度是影响数值计算准确性的重要因素。
(3)综合分析模态频率、应力分布及疲劳寿命的计算结果,发现B10模型建模的复杂性高于B4模型和B6模型,但计算精度与B6模型相差较小,说明B6模型在简化建模方法的同时保证了实体叶片较高的拟真性。
(4)对在役叶片进行疲劳寿命数值预测时,所建立的计算模型对真实叶片损伤行为的还原度,应作为研究的重要评价指标。
(5)为了更加准确地分析不同工况加载顺序及载荷差值对叶片疲劳寿命的影响,应在后续研究中进行叶片复杂载荷作用下的瞬时应力分布计算,为结构的疲劳寿命预测提供更为可靠的载荷参数。
[1] 陶春虎,钟培道,王仁智,等. 航空发动机转动部件的失效与预防[M]. 北京:国防工业出版社,2000:6-18. TAO Chunhu, ZHONG Peidao, WANG Renzhi, et al. Failure Analysis and Prevention for Rotor in Aero-engine[M]. Beijing:National Defence Industry Press, 2000:6-18.
[2] 石可重,赵晓路,徐建中. 重力载荷下风电叶片疲劳数值计算方法研究[J]. 太阳能学报, 2013, 34(2):181-185. SHI Kezhong, ZHAO Xiaolu, XU Jianzhong. Research on Fatigue Numerical Calculation Method of Wind Turbine under Gravity Load[J]. Acta Energiae Solaris Sinica, 2013, 34(2):181-185.
[3] LEYLEK Z, NEELY A J. Development of a Blade Parametric Modeling Methodology for Design and Analysis of Computer Experiments [C]//ASME Turbo Expo 2015:Turbine Technical Conference and Exposition. American Society of Mechanical Engineers. Montreal, 2015:V02BT39A030.
[4] YUN Z, ZHI T C, TAO N. Reverse Modeling Strategy of Aero-engine Blade Based on Design Intent [J]. The International Journal of Advanced Manufacturing Technology, 2015, 81(9/12):1781-1796.
[5] NI K, WANG X Q, MIGNOLET M. Blade Stress Estimation during Multiple Vibratory Modes[C]//Structures, Structural Dynamics, and Materials Conferences. Boston, 2013:2013-1772.
[6] 张强升. 某燃机动叶及压气机组件应力计算与振动分析[D].北京:清华大学, 2011. ZHANG Shengqiang. Stress Calculation and Vibration Analysis of the Gas Turbine Rotor Blade and Compressor Assembly[D]. Beijing:Tsinghua University, 2011.
[7] 栗玉领,徐胜利,杨树桦,等. 非典型气动荷载下压缩机叶轮疲劳强度分析[J]. 机械工程学报, 2015, 51(9):82-89. LI Yuling, XU Shengli, YANG Shuhua, et al. Fatigue Strength Analysis of Compressor Impeller under Non-typical Aerodynamic Load [J]. Journal of Mechanical Engineering, 2015, 51(9):82-89.
[8] DHOPADE P, NEELY A J. Aeromechanical Modeling of Rotating Fan Blades to Investigate High-cycle and Low-cycle Fatigue Interaction [J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(5):052505.
[9] BRANDSEN J D. Prediction of Axial Compressor Blade Vibration by Modelling Fluid-structure Interaction [D]. Stellenbosch:Stellenbosch University, 2013.
[10] 陶海亮,朱阳历,郭宝亭,等. 压气机叶片流固耦合数值计算[J]. 航空动力学报, 2012, 27(5):1054-1060. TAO Hailiang, ZHU Yangli, GUO Baoting, et al. Numerical Simulation of Aeroelastic Response in Compressor Based on Fluid-structure Coupling[J]. Journal of Aerospace Power, 2012, 27(5):1054-1060.
[11] SONG X, WANG L, NIINOMI M, et al. Fatigue Characteristics of a Biomedical β-type Titanium Alloy with Titanium Boride [J]. Materials Science and Engineering:A, 2015, 640:154-164.
[12] RABOTNOV Y N, LECKIE F A, PRAGER W. Creep Problems in Structural Members[J]. Journal of Applied Mechanics, 1969, 37(1):249.
[13] CHABOCHE J L, LESNE P M. A Non-linear Continuous Fatigue Damage Model [J]. Fatigue & Fracture of Engineering Materials & Structures, 1988, 11(1):1-17.
[14] 林杰威. 涡扇发动机风扇叶片疲劳寿命评估与可靠性分析[D].天津:天津大学, 2013. LIN Jiewei. Research on Fatigue Life Estimation and Reliability Analysis of Turbofan Engine Fan Blade[D]. Tianjin:Tianjin University, 2013.
[15] 岳珠峰. 镍基单晶涡轮叶片结构强度设计[M]. 北京:科学出版社,2008:213-232. YUE Zhufeng.Structural Strength Design of Nickel Based Single Crystal Turbine Blade[M]. Beijing:Science Press, 2008:213-232.
[16] 中华人民共和国航空工业部.HB 5277-84 发动机叶片及材料振动疲劳试验方法[S]. 北京:中国标准出版社,1984. Ministry of Aviation Industry of China, HB 5277-84 Test Method for Vibration and Fatigue of Engine Blades and Materials[S]. Beijing:Standards Press of China, 1984.
(编辑 王旻玥)
Numerical Analyses on Fatigue Life for Compressor Blades under Complex LoadsL
ZHANG Junhong LIU Meng FU Xi KOU Haijun LIN Jiansheng
State Key Laboratory of Engines,Tianjin University,Tianjin,300072
In order to improve service life of blades, three blade models were built based on reverse engineering to calculate stress distribution and fatigue life of blades under complex loadings. Considering the influence of centrifugal loads and aerodynamic loads, stress distributions of compressor blades were solved under complex loads. Moreover, the fatigue limit and life prediction model parameters were defined through the fatigue tests, and the fatigue life of compressor blades under the typical working conditions were predicted by nonlinear continuous damage model. Comparing the differences of stress values and fatigue life among three models, results show that the restoration degree of blade geometrical features for the calculation model must be considered when numerical calculations were carried out for blades with complex torsional characteristics.
aero-engine; compressor blade; reverse modeling; complex load; fatigue life
2016-07-05
高等学校博士学科点专项科研基金资助项目(20130032130005);天津市科技支撑计划资助重点项目(13ZCZDGX00200)
V232.4
10.3969/j.issn.1004-132X.2017.12.009
张俊红,女,1962年生。天津大学机械工程学院教授、博士。主要研究方向为动力机械振动及疲劳可靠性。获中国机械工业科学技术奖一等奖1项、国家科学技术进步奖二等奖1项。发表论文130余篇。刘 萌,女,1991年生。天津大学机械工程学院硕士研究生。付 曦(通信作者),女,1990年生。天津大学机械工程学院博士研究生。E-mail:fuxi22@tju.edu.cn。寇海军,男,1984年生。天津大学机械工程学院博士。林建生,男,1960年生。天津大学机械工程学院研究员。

