3-CUR解耦并联3D打印机结构优化与动力学分析
曾达幸 张 星 樊明洲 李晓帆 侯雨雷燕山大学机械工程学院,秦皇岛,066004
3-CUR解耦并联3D打印机结构优化与动力学分析
曾达幸 张 星 樊明洲 李晓帆 侯雨雷
燕山大学机械工程学院,秦皇岛,066004
以熔融沉积成形3D打印机为研究对象,指出现有3D打印机存在的不足,阐述其输出运动特性,提出将解耦并联机构应用于3D打印机。选取3-CUR解耦并联机构作为3D打印机机械本体,论述其合理性,给出其输入输出间的映射关系,得到机构的运动雅可比矩阵和满足空间连续打印的驱动角范围。以灵巧度为目标,进一步优化了机构的驱动角范围,再以打印空间为优化目标,基于遗传算法得到机构参数的最优值。建立机构输入输出的误差模型,分析机构定位精度并进行误差补偿,最后基于牛顿-欧拉方法建立机构的动力学模型并进行验证,为样机设计提供理论依据。
3D打印;解耦并联机构;尺寸优化;定位精度;动力学
0 引言
传统制造工艺利用刀具、模具和机床等通过切割、锻压、弯曲等多道工序进行产品制造,过程相当复杂和漫长[1-3],3D打印技术的诞生使传统加工存在的问题得以解决。目前3D打印技术多达十几种,但成熟应用的主流技术主要有4种[4-5],其中熔融沉积成形(fused deposition modeling,FDM)技术以其结构简单、成形材料范围广泛、成本低的优点应用最广泛[6-8],该技术由Stratasys公司创始人Crump研发,并于1992年研制了第一台商用机型3D-Modeler[9-11]。其后,许多学者开展了基于FDM工艺的3D打印技术的研究。1993年麻省理工学院获得3D实体印刷技术专利,奠定了3D打印技术的基础[12-13]。Z Corporation公司研制了机械结构为串联机构的彩色打印机SpectrumZ510[14],Bowyer等研制了多版本串联机构立体式3D打印机[15-16]。2015年王君等[17]申请了基于Delta并联机械结构的3D打印机专利。3D打印机本体作为3D打印机的主体结构,对3D打印机的性能指标有着决定性的影响,但目前对3D打印机机械结构的研究还比较少。
常见3D打印机从结构形式来分有串联式和并联式。串联式3D打印机的输出形式主要有两种:一种是工作台进行水平面内某一个方向的移动,打印头进行空间另两个方向的移动;另一种是工作台进行竖直方向移动,打印头进行水平面内两个方向的移动。并联式3D打印机的输出形式是工作台固定不动,打印头进行空间三维移动。
对比串联式、并联式3D打印机的特点可知:
(1)串联式3D打印机结构上各轴没有耦合关系,因此控制简单和方便,但本体结构累积误差大,运动惯性较大,使得其动力性能降低,且需要同时控制工作台和打印头才能实现打印,导致打印精度较低。
(2)并联式3D打印机相比于串联式3D打印机,打印精度较高,打印质量比较好,但由于本体机构为Delta机构,各轴具有耦合性,导致调试和控制更困难。
解耦并联式3D打印机继承了两者上述的优点,同时克服了两者上述缺点,采用解耦并联机构作为3D打印机的机械本体有助于提高3D打印机的打印精度、打印速度,解决控制困难等问题。本文提出以解耦并联机构作为3D打印机的本体,并开展解耦并联3D打印机的设计与研究,拓宽3D打印机的构型,对3D打印技术的发展具有一定的借鉴意义。
1 3-CUR解耦并联3D打印机的结构描述
曾达幸等[18]依据约束螺旋型综合法对三自由度移动解耦并联机构进行综合,得到了大量三自由度移动解耦并联机构。本文选择其中具有3个空间平移自由度的3-CUR解耦并联机构作为3D打印机本体机构进行分析与设计。
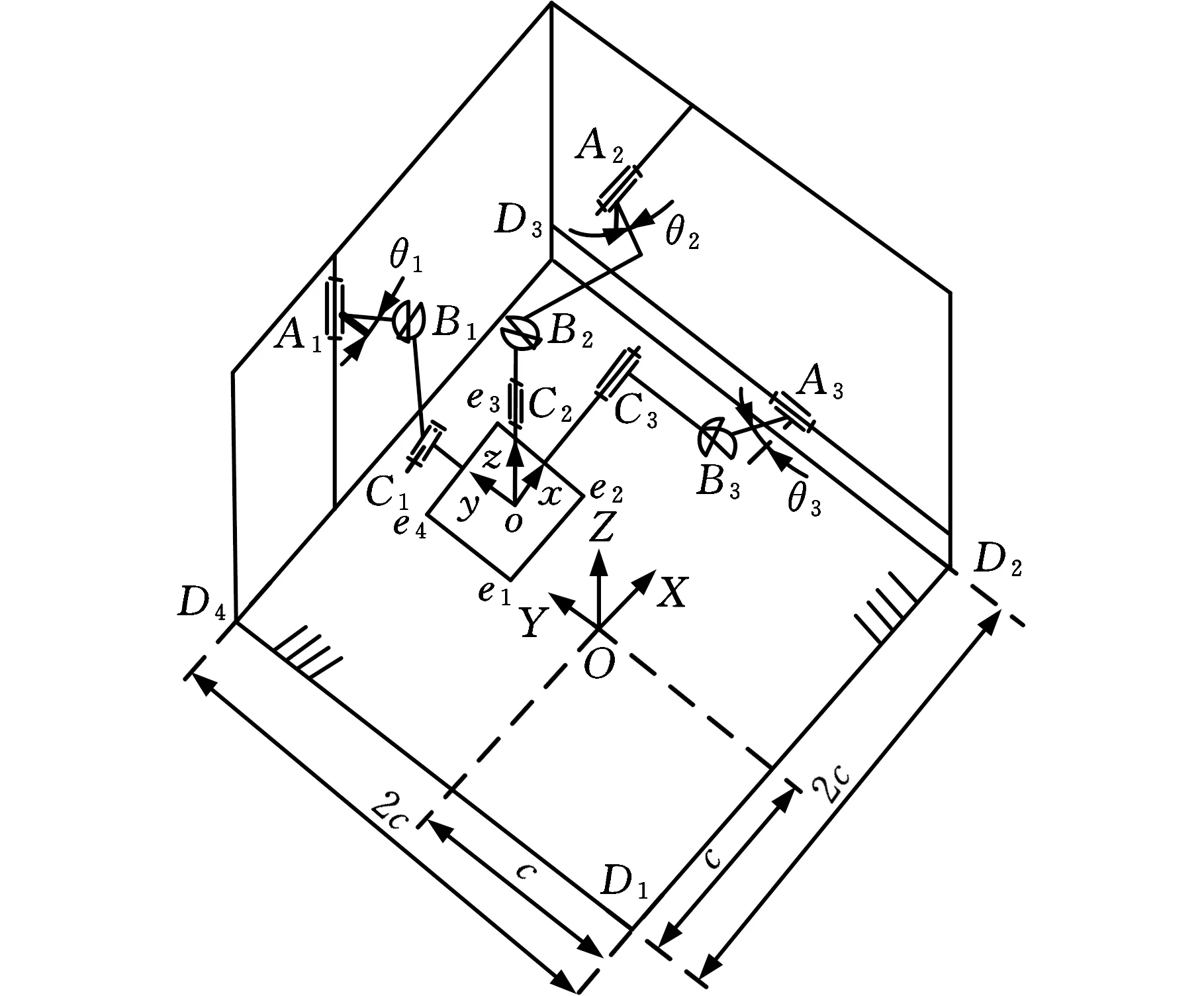
图1 3-CUR解耦并联机构运动简图Fig.1 Kinematic diagram of the 3-CUR decoupled parallel mechanism
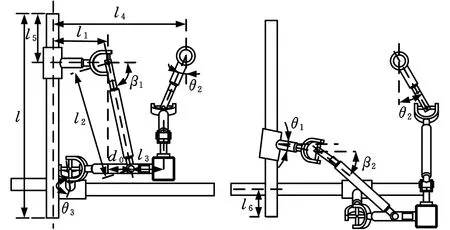
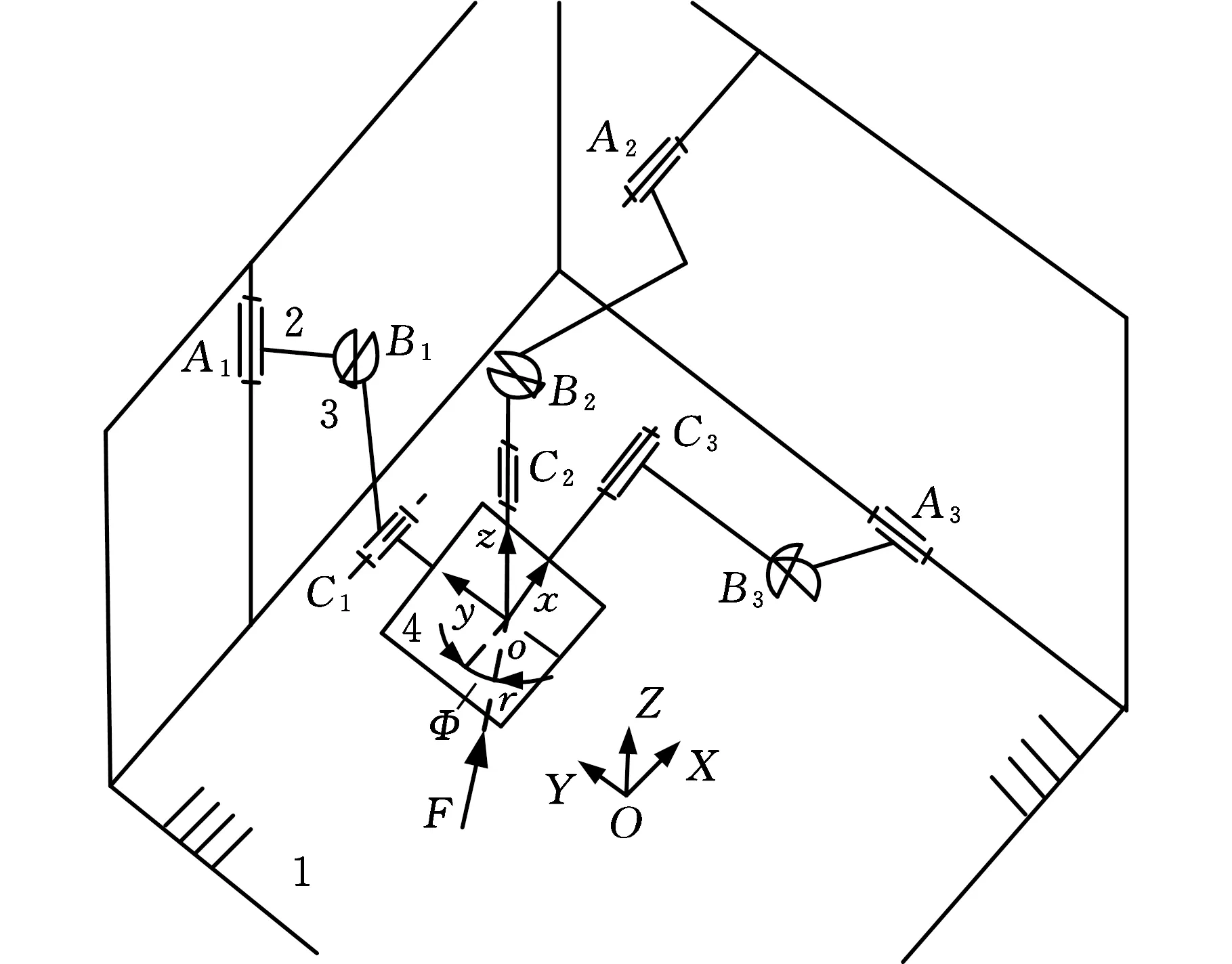
3-CUR解耦并联机构的运动简图见图1。建立以静平台(D1D2D3D4)几何中心为原点的坐标系OXYZ,其中X轴与D1D2平行,Y轴与D2D3平行。建立以动平台(e1e2e3e4)几何中心为原点的坐标系oxyz,其中x轴与e1e2平行,y轴与e2e3平行。设驱动杆AiBi的杆长为l1,连杆BiCi的杆长为l2,连杆Cio的长度为l3,驱动副的转角为θi(i=1,2,3)。3-CUR解耦并联机构的结构简图见图2,动平台通过3条支链分别与轴1、轴2及轴3连接。每条支链包含1个圆柱副A1(图中以转动副代替)、1个虎克铰B1和1个转动副C1,虎克铰的2条轴线中一条与圆柱副轴线平行,另一条与转动副轴线平行。
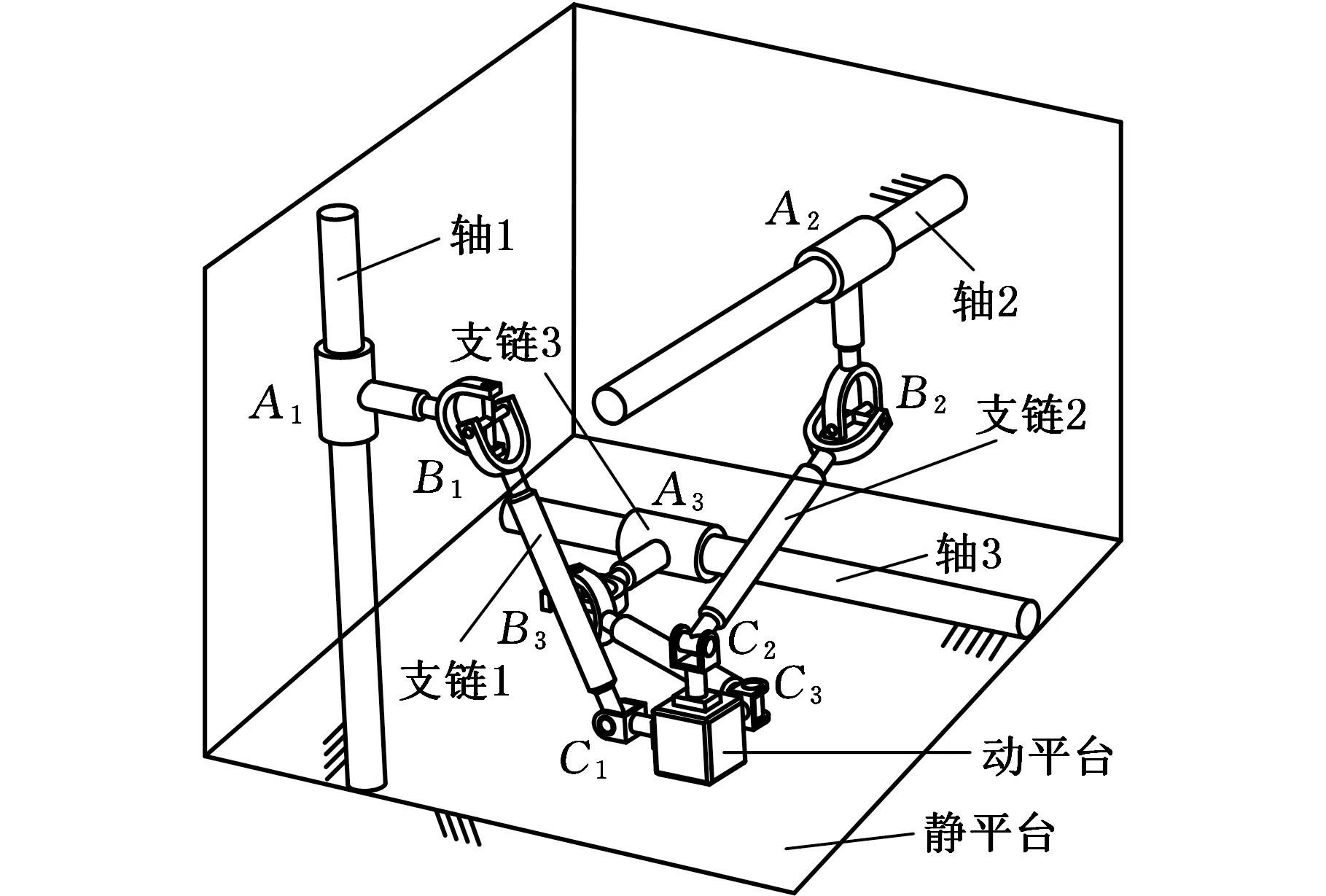
图2 3-CUR解耦并联机构结构简图Fig.2 Schematic diagram of the 3-CUR decoupled parallel mechanism
2 3-CUR解耦并联机构运动学分析
2.1 机构的位置正解和反解
根据输入θi(i=1,2,3)与输出参考点o(x,y,z)的空间位置关系,可知机构的位置正反解方程分别为
(1)
(2)
2.2 空间连续性分析
对式(1)求导,可得机构的运动雅可比矩阵为
(3)
当θi=±90°(i=1,2,3)时,det(J)=0,矩阵的秩减小,机构处于奇异状态。在奇异位形时,经分析可知动平台在工作空间的自由度减少,而3D打印机要求在整个工作空间里必须有3个平移自由度,因此驱动角应选择在[-90°,90°]范围内,才能满足3D打印机工作时的连续性要求。
2.3 运动精度分析
灵巧度是评价3D打印机运动精度的重要指标,它反映了机构输入与输出的失真程度[19],并联机构的灵巧度可用雅可比矩阵的条件数描述,条件数越大,则机构的运动精度越低,当条件数等于1时,机构具有最佳的运动传递性能[20]。
根据机构的运动雅可比矩阵,可知条件数KN为
KN=‖J‖·‖J-1‖
(4)
由上述分析得机构工作状态下驱动角θi(i=1,2,3)范围为[-90°,90°],令θ1,θ2∈[-90°,90°],当θ3分别为-30°、0°、30°时,可得3个打印平面上的条件数性能图谱,如图3所示。
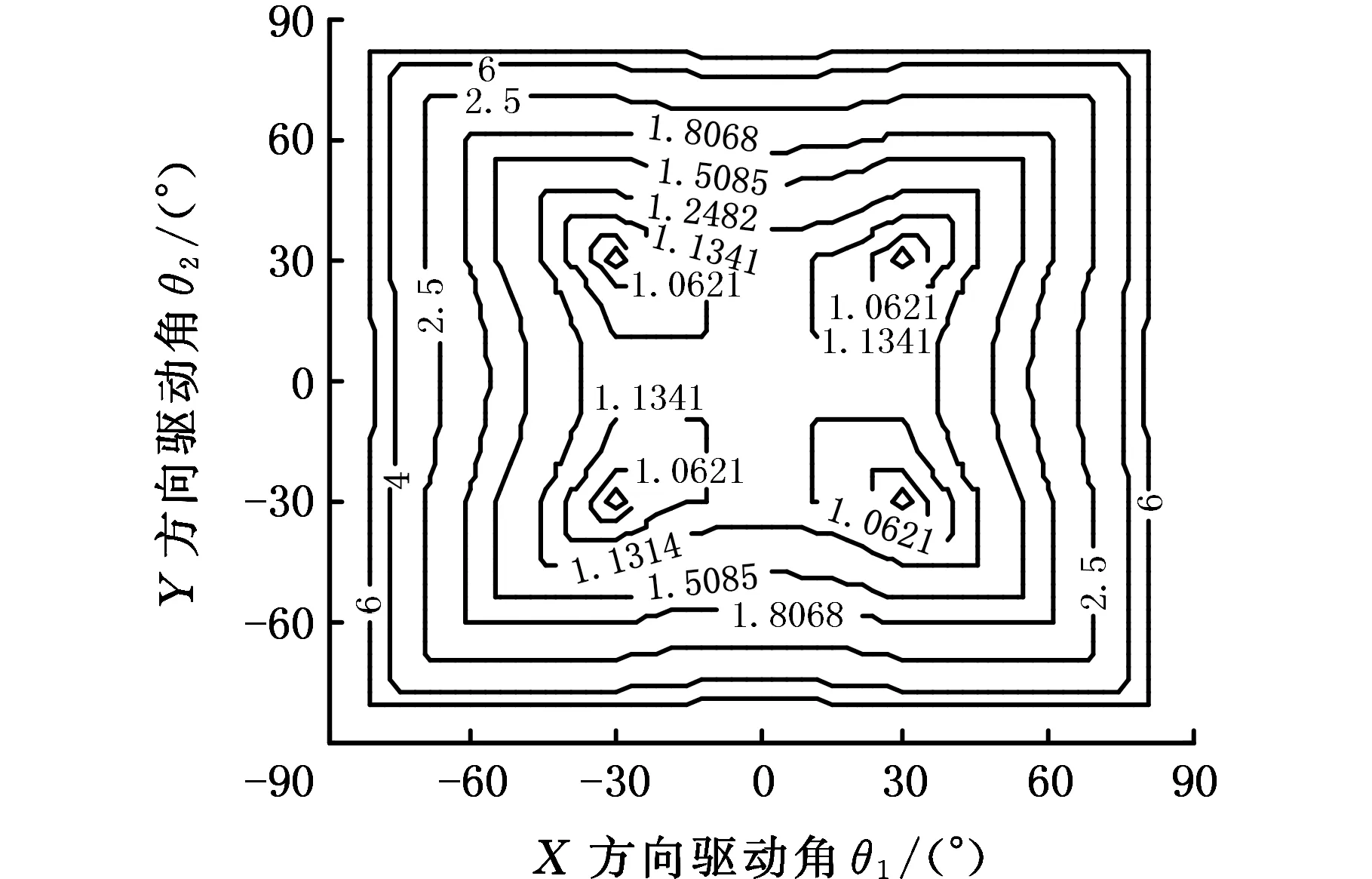
(a)支链3驱动角θ3=-30°
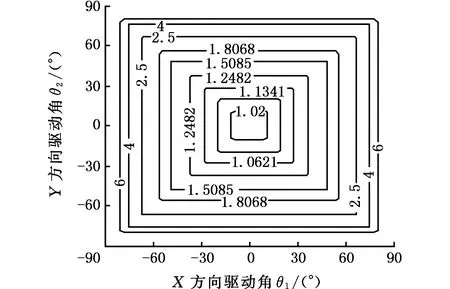
(b)支链3驱动角θ3=0°
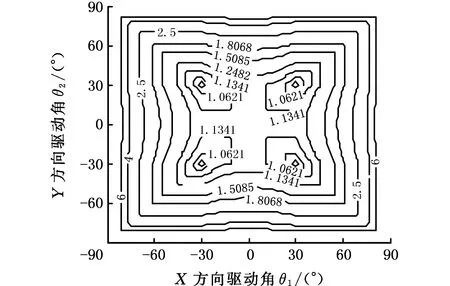
(c)支链3驱动角θ3=30°图3 XY工作平面上驱动角条件数分布性能图谱Fig.3 Distribution performance map of driving angle condition number distribution on XY working plane
由图3可知:①θ3=-30°所在平面条件数分布(图3a)和θ3=30°所在平面条件数分布(图3c)相同,且据2.2节中运动雅可比矩阵可知,驱动角的变化规律为余弦函数,角度的正负不影响函数的值,故得工作空间中垂直方向各层平面上的条件数分布情况关于θ3=0°时对应的工作平面对称。②XY工作平面上中心处条件数最小,从中心到四周条件数逐渐增大,因此打印时应尽量靠近中心打印。③在垂直方向上,θ3=0°对应的XY平面中间区域条件数最小,随着θ3的变化,XY工作平面中心区域条件数逐渐增大,即灵巧度变差。
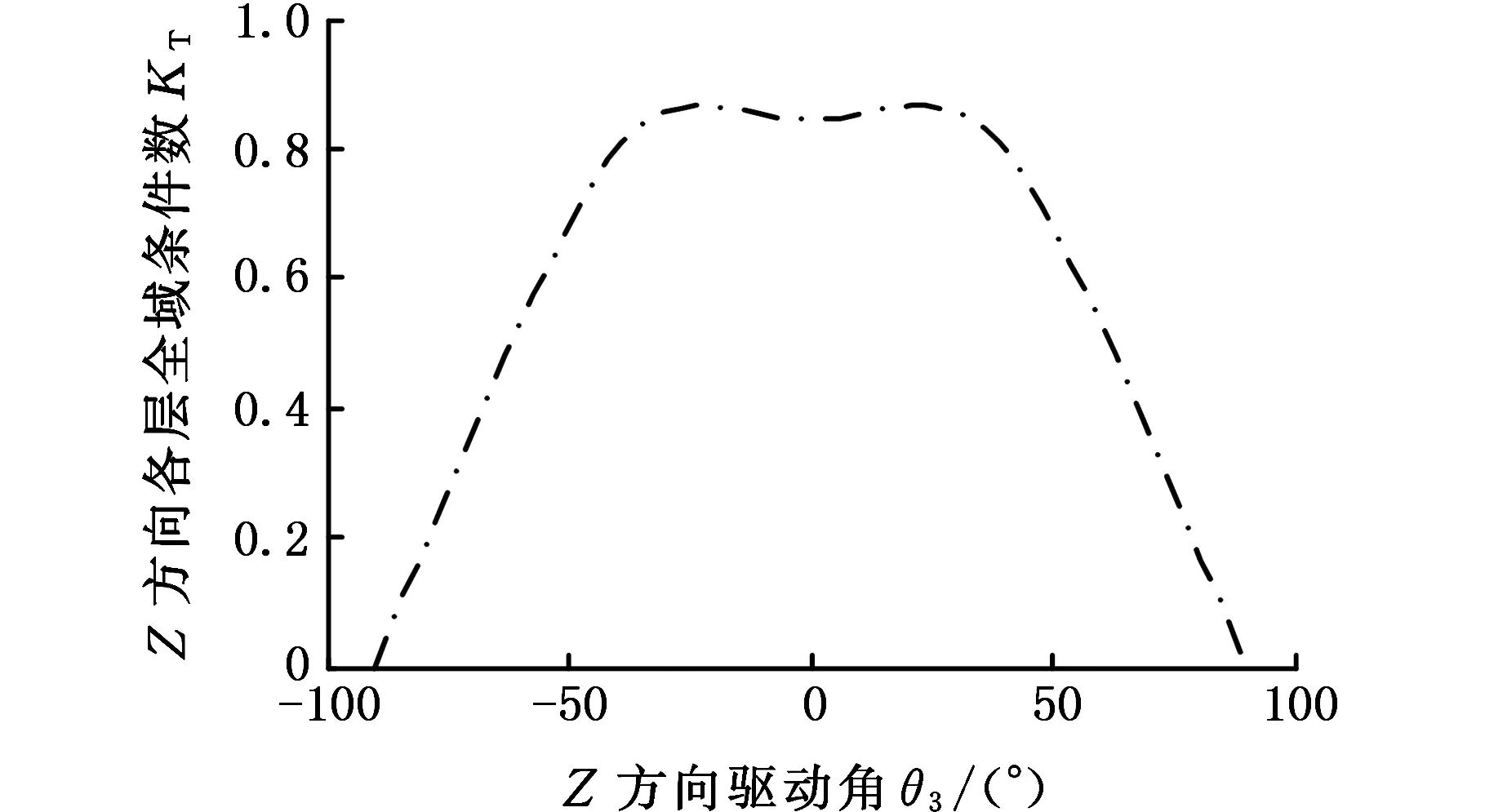
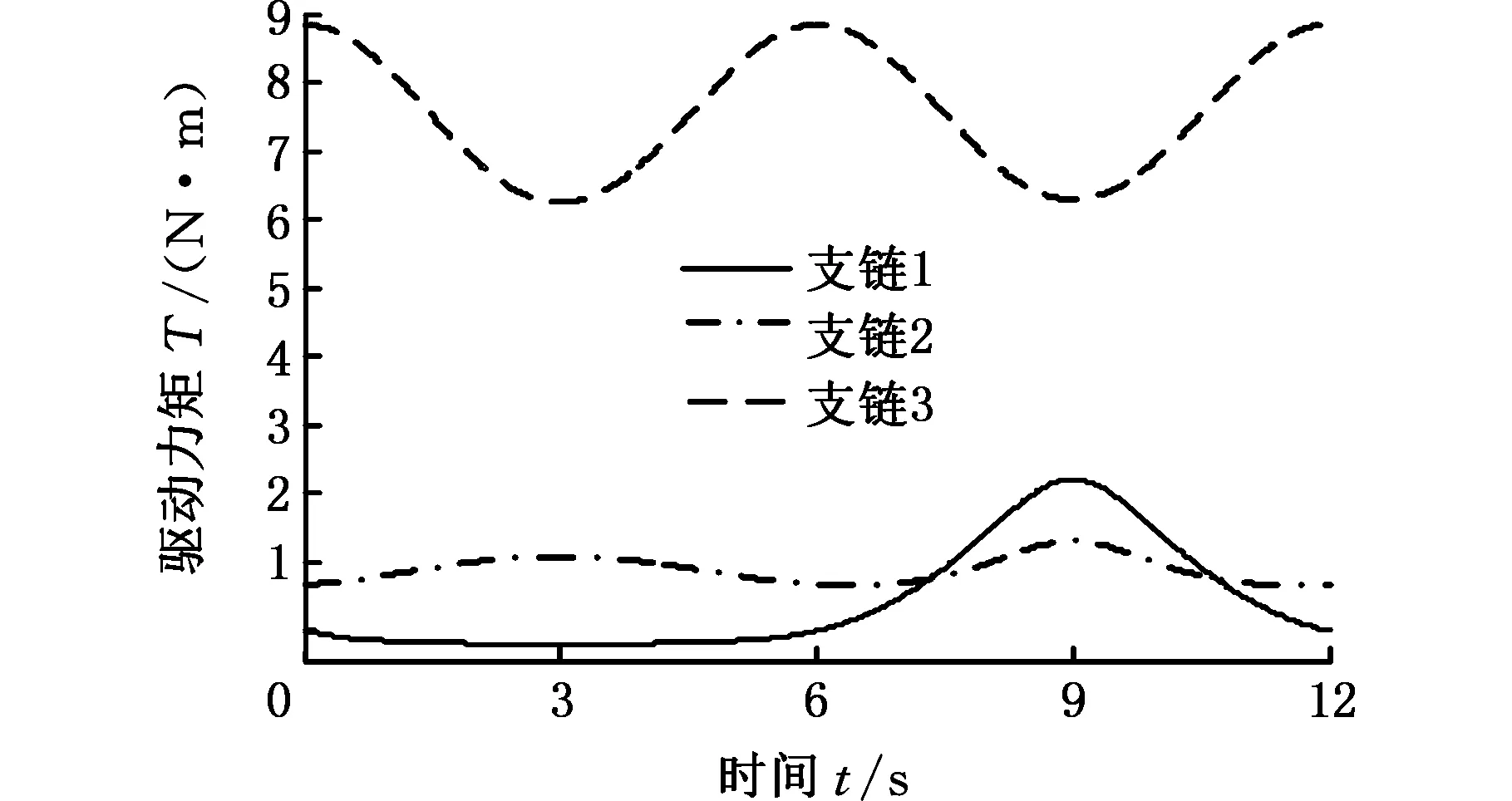
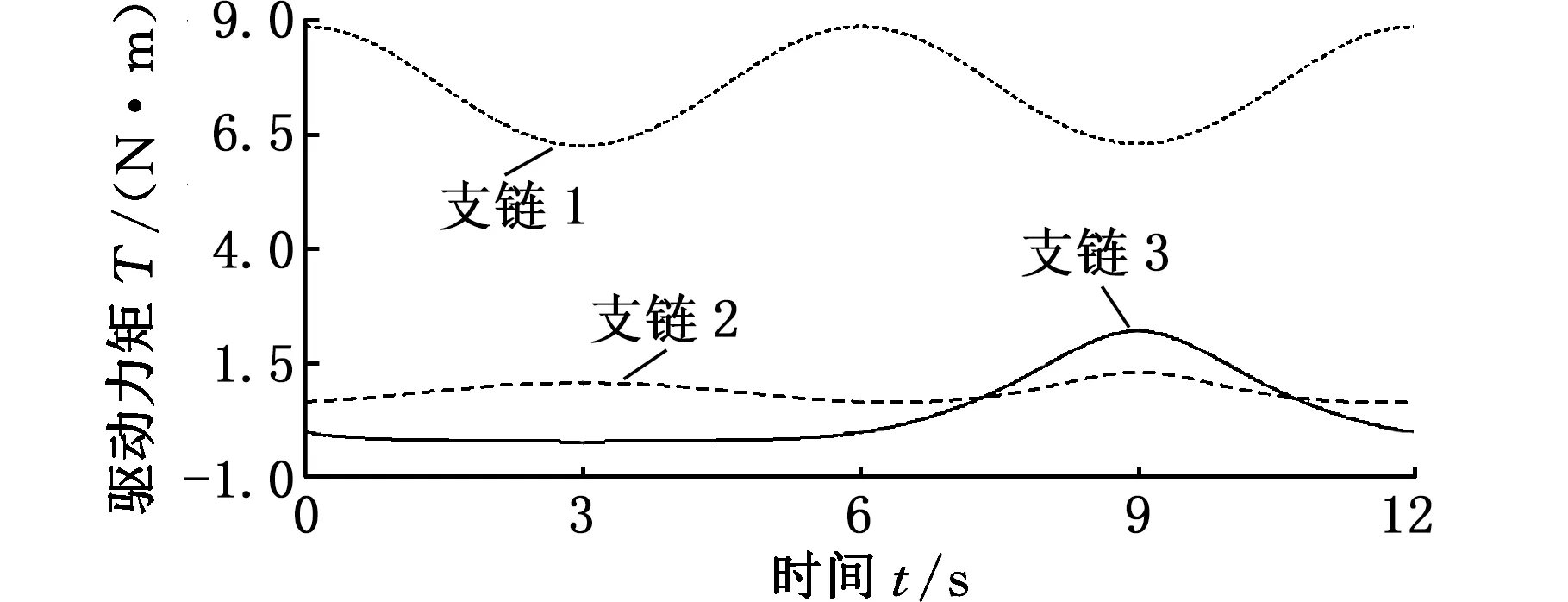
为使每层工作平面上各点都有较高的灵巧度,取整个打印平面条件数范围为1.4 以每层的全域条件数为指标,分析竖直方向上理想驱动角范围内对应的各层灵巧度性能,以此来选择支链3驱动角的范围。3-CUR解耦并联机构工作空间内各层的全域条件数KT为 (5) 式中,w为机构工作平面。 Z方向各层全域条件数与支链3(Z方向)驱动角θ3的变化曲线如图4所示。从图4中可以看出:支链3驱动范围越小,各层的全域条件数越大。为保证打印空间各层均具有优良的灵巧度,支链3驱动角范围也选为[-45°,45°]。 图4 Z方向上各层工作平面上全域条件数分布(θ1,θ2∈[-45°,45°])Fig. 4 Distribution of global conditional number on each working plane in Z direction 本体设计中,机构的尺寸决定3D打印机的工作性能,利用遗传算法可以高效地得到3-CUR解耦并联机构的全局最优解。 首先确定结构参数,取支链1进行分析,动平台的2个极限位置如图5所示,此时支链1的驱动副分别处于上行程极限位置和下行程极限位置,选取l1、l2、l3、β1、β2为机构的设计参数。其中,β1、β2分别为支链1驱动副处于上行程极限位置和下行程极限位置时,驱动杆A1B1轴线与连杆B1C1轴线的夹角。 (a)上行程极限位置 (b)下行程极限位置图5 3-CUR解耦并联机构运动状态Fig.5 Motion state of the 3-CUR decoupled parallel mechanism 机构处于图5中状态时,约束方程为 l1+l2cosβ1+l3+l1sinθ2=l4 (6) l1cosθ1+l2cosβ2+l3=l4+l1sinθ2 (7) (8) 式中,l4为支链1与支链2轴线的距离;l5为支链1驱动副位于上行程极限位置时,驱动杆A1B1轴线到轴1顶端的距离;l6为轴3轴线到轴1底端的距离;l为轴1的长度。 分析可知,l2和l3分别与l1具有线性关系,所以待优化参数为l1、β1、β2。给定结构参数优化区域如下: l1∈[80 mm,90 mm]β1∈[80°,90°] β2∈[36°,45°] 以打印空间为目标函数,将打印空间的大小作为个体的适应度。根据机构运动规律得打印空间形状边长f的计算公式为 (9) 设定遗传算法的参数:交叉概率Pc=0.9,变异概率Pm=0.1,遗传代数为100,得到打印空间取得最大时的全局最优解: [l1β1β2]=[86.175 mm 89.998° 36.496°] 同时可得遗传算法的寻优性能跟踪图(图6)。 图6 3-CUR解耦并联机构工作空间的寻优性能跟踪图Fig. 6 The optimal performance tracking graph of working space of 3-CUR decoupled parallel mechanism 分析可知,随着遗传代数的增加,目标函数逐渐趋于稳定,从而得到目标函数的最优解。 定位精度是衡量3D打印机性能的重要指标,关系着打印的紧密性。机构姿态误差是不可补偿的,但可以通过提高制造精度、改善装配工艺来减小姿态误差;位置误差是可补偿的,通过控制输入对位置误差进行补偿[21]。 4.1 机构的位置误差建模 根据全微分理论,由位置正解方程可得机构的误差模型为 δP=Jθδθ+JUδU (10) 式中,δP为动平台的输出误差;Jθ为驱动参数的误差传递矩阵;δθ为驱动参数误差;JU为杆件参数的误差传递矩阵;δU为杆件制造误差。 4.2 机构精度分析 4.2.1 输入参数误差对定位精度的影响 为了分析机构的输入参数误差对打印误差的影响,以输出误差δP表示打印机打印误差的大小[22],其表达式为 (11) 式中,δPX、δPY、δPZ为打印误差在X、Y、Z方向上的误差分量。 假设杆件参数误差为0,支链3的输入参数误差不影响打印工作平面上的定位误差。给定输入参数误差δθ1= δθ2=0.05°和δθ3=0°,得到水平工作平面上输入角的变化对δP的影响规律如图7所示。 图7 输入参数误差对定位精度的影响Fig.7 Effect of input parameter error on positioning accuracy 分析可知,打印误差从中心向四周逐渐变小,输入参数误差小于等于0.05°时,对打印精度影响较小。 4.2.2 杆件制造误差对定位精度的影响 假设输入参数误差为0,取δl1=0.1 mm时,杆件制造误差对定位精度的影响规律如图8所示。 图8 杆长对定位精度的影响Fig.8 Effect of the length of the rod on the positioning accuracy 分析可知,打印误差在打印平面上由中心向四周逐渐增大,其最大值等于杆件制造误差的大小。 4.3 误差模型的补偿和可行性分析 令δP=0,由机构误差模型可得位置精度补偿数学模型为 (12) 给定机构一个输出位置(X,Y,Z)和位置误差δPX, δPY,δPZ,如表1所示,可以求得名义补偿量δθ01、δθ02、δθ03分别为-4.916×10-4mm、-5.756×10-4mm、4.084×10-4mm和输入的实际误差补偿量δθ1、δθ2、δθ3分别为0.0204 mm、0.0237 mm、-0.0194 mm。 表1 位置参数和位置误差 进行输入补偿后,位置误差δPX、δPY、δPZ分别为0.0804 mm、0.0950 mm、-0.0661 mm。 可以看出,对误差模型进行补偿后,机构的位置误差明显减小,机构的定位精度得到了提高。 3D打印机是一种高精密的机器,在其工作过程中应运行平稳、定位准确,以保证打印平面的平整性及各层之间的粘结紧密性,因此对机构进行动力学分析是十分必要的。由于各支链结构相同,故取支链1为研究对象。 图9 3-CUR解耦并联机构受力简图Fig.9 Force diagram of the 3-CUR decoupled parallel mechanism 5.1 动力学模型的建立 (13) 根据式(13)可得各构件的力平衡方程为 (14) (15) (16) (17) 式中,Fi为外界施加于支链i主动构件上的力。 合并式(14)~式(17)可得单支链对动平台的作用力: (18) 在3个分支和外力的共同作用下,动平台处于平衡状态,其力平衡方程为 (19) 式中,F为作用在动平台上的外力。 同理可得动平台的力矩平衡方程为 (20) 将式(18)代入式(20),得动平台力矩平衡方程为 (21) 由式(21)可得Fi在定坐标系下的表达式,从而求得其动力学反解。 5.2 机构动力学模型验证 设定参数如下:驱动杆和连杆BiCi质量分别为:im1=1 kg和im2=2 kg(i=1,2,3),动平台质量m4=4 kg,驱动杆和连杆BiCi的杆长分别为l1=86 mm和l2=170 mm,其转动副与动平台质心的距离分别为l3=67 mm和l4=216 mm,给定动平台轨迹为 (22) 利用MATLAB软件,得到驱动力矩随时间的变化曲线如图10所示,导入ADAMS中得到驱动力矩随时间的变化曲线如图11所示,通过对比发现,曲线变化基本相同,从而验证了动力学模型的正确性。 图10 驱动力矩数值解变化曲线Fig.10 Variation curve of numerical solution of driving torque 图11 驱动力矩仿真变化曲线Fig.11 Simulation curves of driving torque 5.3 样机制造 图12 3-CUR解耦并联3D打印机的样机Fig.12 The 3-CUR decoupled parallel 3D printer prototype 分析各支链中的杆件、动平台和静平台的受力情况、加工特性和装配要求,经过结构设计和合理选材,完成了3-CUR解耦并联3D打印机的控制电路设计和机械本体加工,如图12所示;完成了机械和电气接口的连接;经过调试和产品打印,结果表明,本样机能准确定位和打印出预期的产品,验证了理论的正确性和结构设计的合理性。 (1)分析现有3D打印机结构存在的问题,提出将3-CUR解耦并联机构应用于3D打印机本体机构,拓展3D打印机机构构型。 (2)通过运动学分析,得到了机构的位置正解和反解方程,通过分析机构的条件数,优化了支链的驱动角,保证机构的运动精度,以打印空间为优化目标,利用遗传算法得到了机构参数的最优值。 (3)利用机构的输入输出微分关系,建立机构的定位误差模型,分析机构的定位精度,提出了改善定位精度的误差补偿模型;最后建立机构的动力学模型,并验证了动力学模型的正确性,为最终样机的设计奠定基础。 [1] 朱艳青, 史继富, 王雷雷, 等. 3D打印技术发展现状[J].制造技术与机床, 2015(12):50-57. ZHU Yanqing, SHI Jifu, WANG Leilei, et al. Current Status of 3D Printing Technology[J]. Manufacturing Technology and Machine Tools, 2015(12):50-57. [2] 李小丽, 马剑雄, 李萍, 等. 3D打印技术及应用趋势[J].自动化仪表, 2014, 35(1):1-5. LI Xiaoli, MA Jianxiong, LI Ping, et al. 3D Printing Technology and Its Application Trend[J]. Process Automation Instrumentation, 2014, 35(1):1-5. [3] 卢秉恒, 李涤尘. 增材制造(3D打印)技术发展[J]. 机械制造与自动化, 2013,42(4):1-4. LU Bingheng, LI Dichen. Development of the Additive Manufacturing (3D printing) Technology[J]. Machine Building & Automation, 2013,42(4):1-4. [4] 孙柏林. 试析“3D打印技术”的优点与局限[J]. 自动化技术与应用, 2013, 32(6):1-6. SUN Bolin. An Analysis of the Advantages and Limitations of “3D Printing Technology”[J]. Techniques of Automation & Application, 2013, 32(6):1-6. [5] 蒋伟辅. 快速成形技术综述[J]. 机械工程与自动化, 2011(6):214-216. JIANG Weifu. Summary on Rapid Prototyping[J]. Mechanical Engineering & Automation, 2011(6):214-216. [6] 谭永生. FDM快速成形技术及其应用[J]. 航空制造技术, 2000(1):26-28. TAN Yongsheng. FDM Rapid Prototyping Technology and Its Application[J]. Aeronautical Manufacturing Technology, 2000(1):26-28. [7] 唐通鸣, 张政, 邓佳文, 等. 基于FDM的3D打印技术研究现状与发展趋势[J]. 化工新型材料, 2015,43(6):228-230. TANG Tongming, ZHANG Zheng, DENG Jiawen, et al. Research Status and Trend of 3D Printing Technology Based on FDM[J]. New Chemical Materials, 2015,43(6):228-230. [8] 吴涛, 倪荣华, 王广春. 熔融沉积快速成形技术研究进展[J]. 科技视界, 2013(34):94-94. WU Tao, NI Ronghua, WANG Guangchun. Research Progress of Fused Deposition Rapid Prototyping Technology[J]. Science & Technology Vision, 2013(34):94-94. [9] 赵萍, 蒋华, 周芝庭. 熔融沉积快速成形工艺的原理及过程[J]. 机械制造与自动化, 2003,32(5):17-18. ZHAO Ping, JIANG Hua, ZHOU Zhiting. The Technology Theory and Process for Fused Deposition Modeling Rapid Prototyping[J]. Machine Building & Automation, 2003,32(5):17-18. [10] 罗晋, 叶春生, 黄树槐. FDM系统的重要工艺参数及其控制技术研究[J]. 锻压装备与制造技术, 2005,40(6):77-80. LUO Jin, YE Chunsheng, HUANG Shuhuai. The Study on the Important Technologic Parameters and Their Control of FDM System[J]. China Metal Forming Equipment & Manufacturing Technology, 2005,40(6):77-80. [11] 额日登布鲁格. 3D打印技术的理论与实践[D]. 北京:中共中央党校, 2015. Eridengbuluge. Theory and Practice of 3D Printing Technology[D]. Beijing:Party School of the Central Committee of CPC, 2015. [12] 杨明. FDM快速成形机的结构设计及优化研究[D].武汉:华中科技大学, 2009. YANG Ming. Structural Design and Optimization on FDM Rapid Prototyping Machine[D]. Wuhan:Huazhong University of Science and Technology, 2009. [13] LIPSON H, KURMAN M. Fabricated:the New World of 3D Printing[M]. Indiana:John Wiley & Sons, 2013. [14] RANDALL N. 3D System Ships Project SD 3000 for In-office 3DPrinting[J]. Engineering Automation Report, 2008, 17(19):294-300. [15] LEMU H G, KURTOVIC S. 3D Printing for Rapid Manufacturing:Study of Dimensional and Geometrical Accuracy[M]. Berlin:Springer, 2012. [16] OLLIVER V. RepRap: the Replicating Rapid Prototyper: Maximizing Customizability by Breeding the Means of Production[EB/OL].(2010-05-02).htPS://reprep.org/wiki/Future Plan. [17] 王君, 孙金风, 游颖, 等. 一种基于Delta并联机械结构的3D打印机:中国,CN104527066A[P]. 2015-04-22. WANG Jun, SUN Jinfeng, YOU Ying, et al. The 3D Printer Based on Delta Parallel Mechanical Structure:China, CN104527066A[P]. 2015-04-22. [18] 曾达幸, 李晓帆, 邱雪松,等. 新型三平移解耦并联机构的综合[J]. 中国机械工程, 2015, 26(10): 1279-1283. ZENG Daxing, LI Xiaofan, QIU Xuesong, et al. Type Synthesis of a Novel Three Degree of Freedom Translational Decoupled Parallel Mechanism[J]. China Mechanical Engineering, 2015, 26(10):1279-1283. [19] 黄田, 倪雁冰, 王洋, 等. 3-HSS并联机床运动学设计[J].制造技术与机床, 2000(3):10-12. HUANG Tian, NI Yanbing, WANG Yang, et al. Kinematic Design of 3-HSS Parallel Machine Tool[J]. Manufacturing Technology & Machine Tool, 2000(3):10-12. [20] 黄真, 孔令富, 方跃法. 联机器人机构学理论及控制[M]. 北京:机械工业出版社, 1997:1-3. HUANG Zhen, KONG Lingfu, FANG Yuefa. Theory and Control of Parallel Robot Mechanism[M]. Beijing:Mechanical Industry Press, 1997:1-3. [21] 刘爱荣, 马履中, 杨文亮, 等. 3-PRUR三平移并联机构机器人的精度分析[J]. 机械制造, 2009, 47(2):27-29. LIU Airong, MA Lyuzhong, Yang Wenliang, et al. Precision Analysis of 3-PRUR Three Translational Parallel Mechanism Robot[J]. Machinery, 2009, 47(2):27-29. [22] 刘向东. 3-PRR平面并联机器人运动仿真研究及精度分析[D]. 镇江:江苏科技大学, 2012. LIU Xiangdong. Motion Simulation and Accuracy Analysis of 3-PRR Planar Parallel Robot[D]. Zhenjiang:Jiangsu University of Science and Technology, 2012. (编辑 苏卫国) Structure Optimization and Dynamics Analysis of 3-CUR Decoupled Parallel 3D Printers ZENG Daxing ZHANG Xing FAN Mingzhou LI Xiaofan HOU Yulei Taking a 3D printer of fused deposition modeling as the research object, the shortages of the present 3D printers were pointed out, the ouPSut motion characteristics were expounded and a decoupled parallel mechanism would be applied to the 3D printers. Selecting 3-CUR decoupled parallel mechanisms as the mechanical body of 3D printers and discussing its rationality, the mapping relations among inputs and ouPSuts were given, the kinematic Jacobian matrix and the ranges of driving angles that supported continuous printing were obtained. Aimed at dexterity, the ranges of driving angles of the mechanism were optimized. Then aimed at the printing spaces, the genetic algorithm was introduced to get the optimal values of the mechanism parameters. By establishing the error model among inputs and ouPSuts of the mechanism, analyzing the positioning accuracy of the mechanism and compensating the errors, the dynamics model of mechanism was established and verified based on Newton-Euler method, which provides theoretical basis for designs of the prototypes. 3D print; decoupled parallel mechanism; size optimization; positioning accuracy; dynamics 2016-08-01 河北省高等学校科学技术研究青年基金资助项目(QN2014175);河北省科学技术研究与发展计划资助项目(15211826) TH112 10.3969/j.issn.1004-132X.2017.12.005 曾达幸,男,1978年生。燕山大学机械工程学院副教授。主要研究方向为并联机构型综合、并联机器人和重型工程机械设计等。张 星,男,1989年生。燕山大学机械工程学院硕士研究生。樊明洲,男,1992年生。燕山大学机械工程学院硕士研究生。李晓帆,男,1988年生。燕山大学机械工程学院硕士研究生。侯雨雷(通信作者),男,1980年生。燕山大学机械工程学院教授、博士研究生导师。E-mail:ylhou@ysu.edu.cn。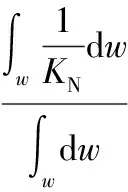
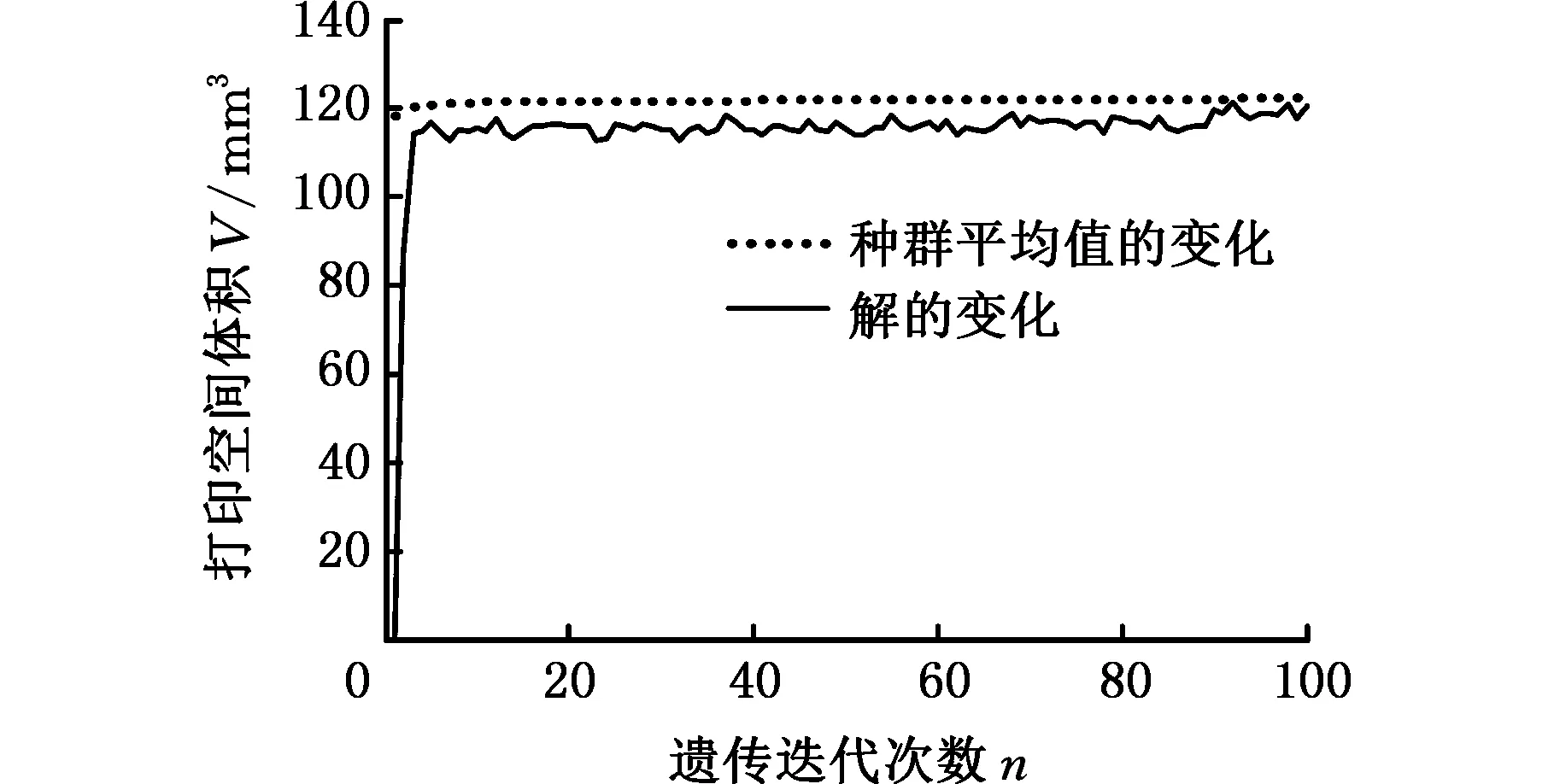
3 3-CUR解耦并联机构打印空间优化



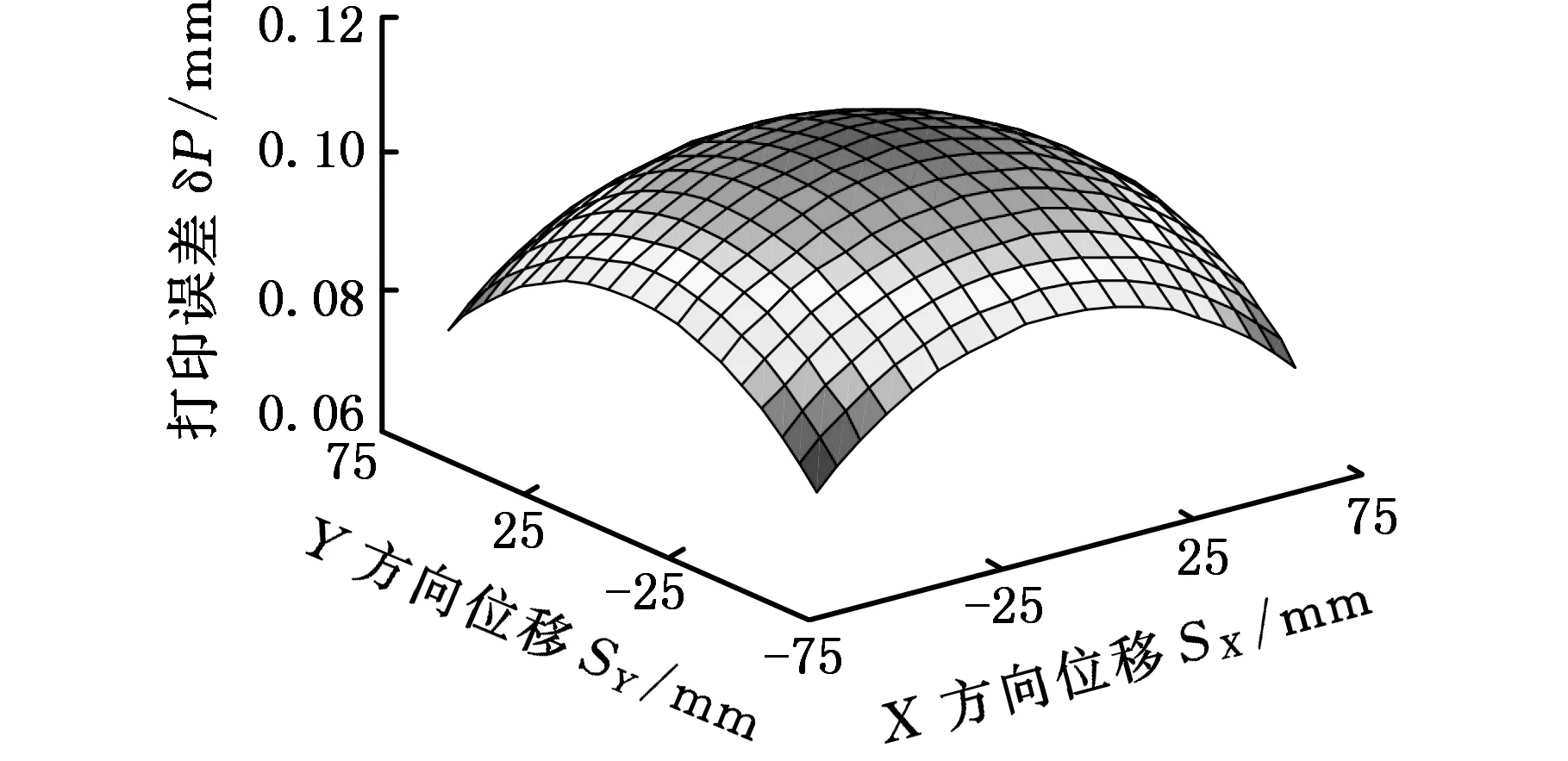
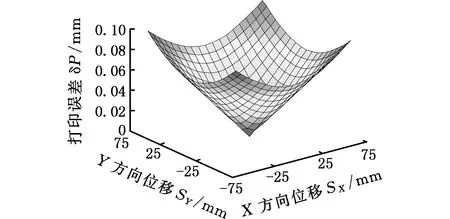
4 3-CUR解耦并联机构定位精度分析


5 3-CUR解耦并联机构动力学分析

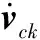
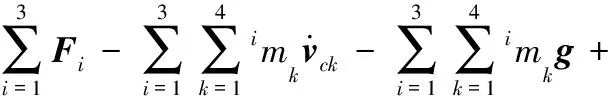

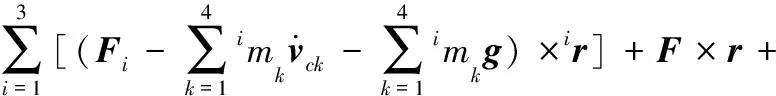


6 结论
School of Mechanical Engineering,Yanshan University,Qinhuangdao,Hebei,066004

