工程机械柔性机械臂振动的混合可靠性分析
曾 光 姜 潮 倪冰雨.湖南大学汽车车身先进设计制造国家重点实验室,长沙,400822.中联重科股份有限公司,长沙,4003
工程机械柔性机械臂振动的混合可靠性分析
曾 光1,2姜 潮1倪冰雨1
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100822.中联重科股份有限公司,长沙,410013
基于概率-区间混合不确定性模型及结构可靠性分析方法,针对工程机械多关节柔性机械臂的振动可靠性进行研究。根据机械臂不确定参数的信息完备程度,通过概率变量和区间变量对不确定参数进行度量。基于柔性臂架有限元仿真数据,构建机械臂参数与结构固有频率关系的径向基函数代理模型,进而通过概率-区间混合可靠性分析方法对机械臂共振的失效概率进行区间估计。最后将该方法应用于实际产品,通过工程实例验证了方法的有效性。
柔性机械臂;振动分析;概率-区间混合模型;径向基代理模型
0 引言
在实际工作中,机械臂各关节角度均为不确定性参数,构型变化多样,臂架的系统固有频率也随之变化较大,各构型下的动态响应存在不确定性,当外界载荷频率与系统固有频率接近时,将产生共振并造成结构快速失效,若仍然采用确定性的静态分析方法则不能反映上述工程特点,其分析结果也难以反映工程实际,因此,为实现大型工程机械装备在复杂工况下有效安全地作业,需要针对上述机械臂振动进行基于不确定性的结构可靠性分析。
对于多关节机械臂可靠性的研究,目前国内外已有一些研究成果。文献[1]根据机器人机械臂各运动参数的概率信息,对机器人机械臂的总体可靠度进行了评价。考虑到随机因素的影响,文献[2]将随机因子法引入随机响应面中,提出了一种处理多输入随机参数的双连杆机械臂系统可靠性分析方法。通过将机械臂分为装配体结构和单体结构,文献[3]对工业机器人机械臂进行了模态分析,并借助于ANSYS的概率分析模块对机械臂进行了可靠性研究。考虑到工程机械臂的加工制造误差等不确定性因素,文献[4]基于概率方法构建了不确定性对机械臂运动学和动力学的作用机制模型,并进行了运动学和动力学可靠性研究。由于冗余自由度多关节机械臂具有灵活度高、避障能力和抗故障风险强的特性,文献[5]将整个任务分解为多个步骤,最终对机械臂完成整项任务的可靠度进行了估计。考虑到弹性因素的影响,文献[6]构建了机械臂端部执行器位姿精度的多级模型,实现了对机械臂运动精度的可靠性分析。上述研究多集中于关节较少、尺寸较小的机械臂机构可靠性方面,而对于多关节柔性机械臂的结构可靠性,尤其是在振动外载荷作用下的可靠性研究报道目前并不多见。并且,目前对工程机械臂架的可靠性分析多集中于概率假设,即认为不确定因素服从某种概率分布函数;然而在实际工程中,由于施工工况复杂多变、试验可测数据有限等原因,有些参数的概率分布函数难以精确获取甚至不存在。研究表明[7],对于此类参数的不当概率假设可导致对结构可靠性的估计产生较大的偏差,反而增大了工程机械在实际施工中的失效风险。
针对上述问题,本文提出了一种基于概率-区间混合不确定性的柔性机械臂振动可靠性分析方法。通过在柔性机械臂可变构型范围空间内建立振动可靠性分析中动力学特性变量关于构型不确定性参量的响应面函数,并基于构型-动力学特性响应面函数及激励载荷情况,建立概率-区间混合可靠性分析模型,最终采用迭代解耦方法进行求解。
1 柔性机械臂架振动可靠性分析
诸如混凝土泵车、工程起重机、消防车等车载工程机械装备主要由底盘、动力传输系统和臂架系统组成,臂架系统是其最关键的部件之一。例如,对于混凝土泵车,混凝土主要通过臂架系统连续不断地泵送到浇注点,因此臂架性能的好坏直接影响混凝土浇注质量。
目前柔性机械臂架系统在设计上趋于轻型化,而且随着臂杆长度不断增大,臂架的柔性影响越来越明显。由于多关节机械臂结构始终处于动载荷作用下,臂架系统会出现一定程度的低频振动,这种低频振动不仅不利于臂架系统的控制和末端定位,而且会加速臂架的疲劳破坏。此外,当机械臂工作于特定工况、伸展成特定姿态、动态载荷频率与臂架固有频率接近至一定程度时,臂架就开始剧烈摇晃并导致动应力显著增大,因此准确了解各工况下臂架结构固有频率与动态载荷特征尤为重要。
对于柔性机械臂的振动可靠性评估,其不确定性主要来源于载荷的不确定性和动力学特性的不确定性。载荷的不确定性包括频率、大小和作用形式等的不确定性。动力学特性的不确定性则包括两个方面:第一,结构的几何尺寸、材料属性、制造工艺、时变损伤、关节间隙、动力学求解方法等的影响难以精确确定,造成即使已知柔性机械臂的构型,数学模型的动力学特性预测结果也会与实际情况存在一定的差异;第二,柔性机械臂是一个多自由度系统,工作过程中构型在不断变化,构型的变化将会造成机械臂动力学特性的显著变化。对于实际工程问题,由于试验条件限制和实际工况的不可预知性,有些不确定性参数因试验样本的充足可以构建精确的概率分布(如机械臂的振动载荷),而有些参数因样本缺乏只能给定其变化区间(如决定机械臂工作构型的各个关节角度等)。仅仅基于概率理论进行可靠性分析很难精确得到所有不确定变量的概率分布函数,采用概率-区间混合模型进行柔性机械臂的振动可靠性评估为目前较具实际工程意义的处理方法。
1.1 机械臂共振的概率可靠性分析
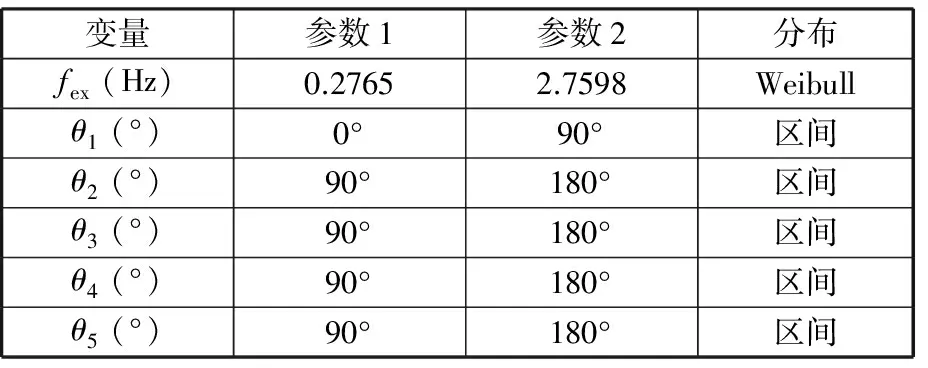
工程中一般认为结构固有频率落入载荷激振频率一定范围内时发生共振失效,记Ωf为机械臂架共振导致结构失效时结构固有频率fd的集合,则Ωf可表示为
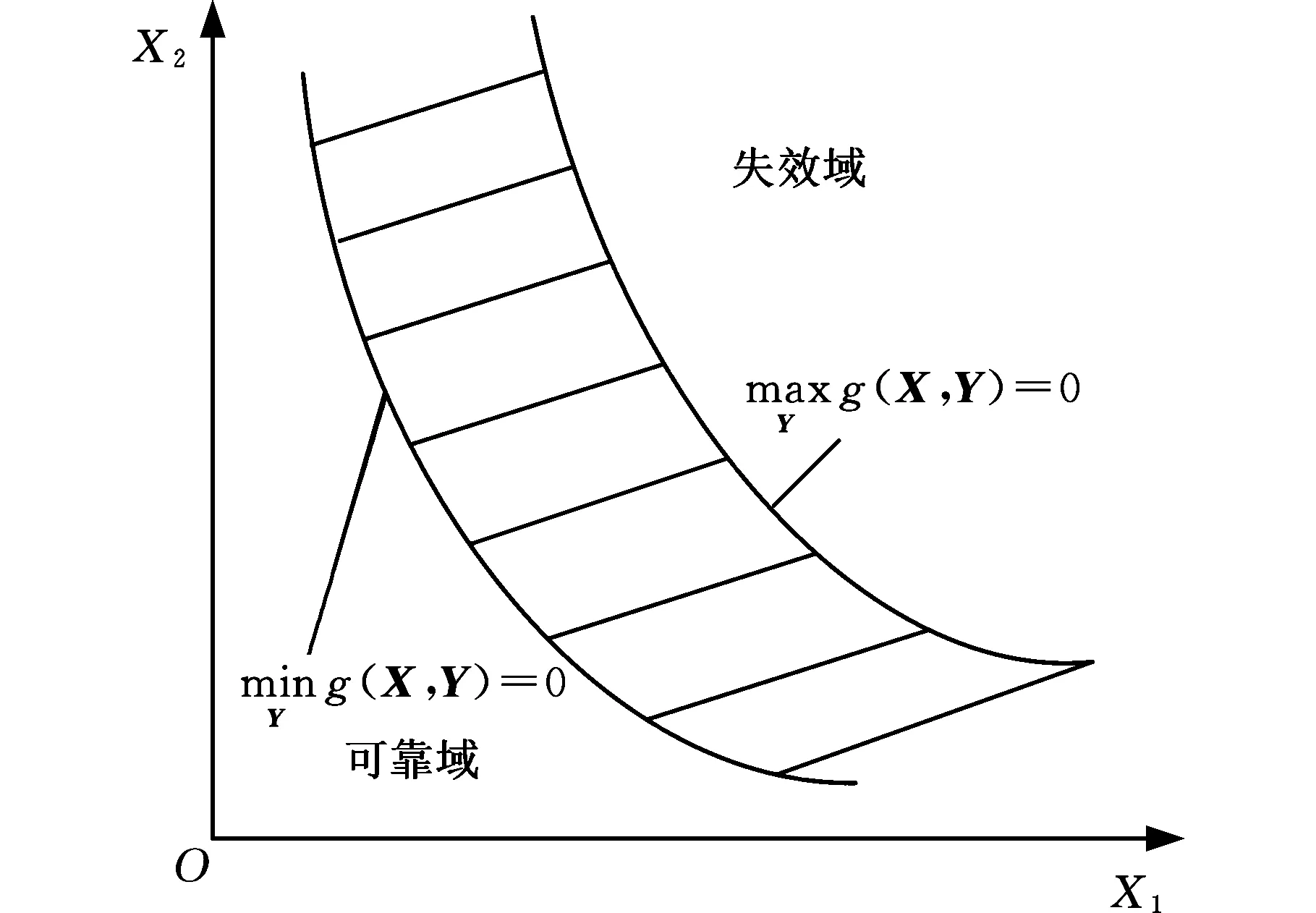
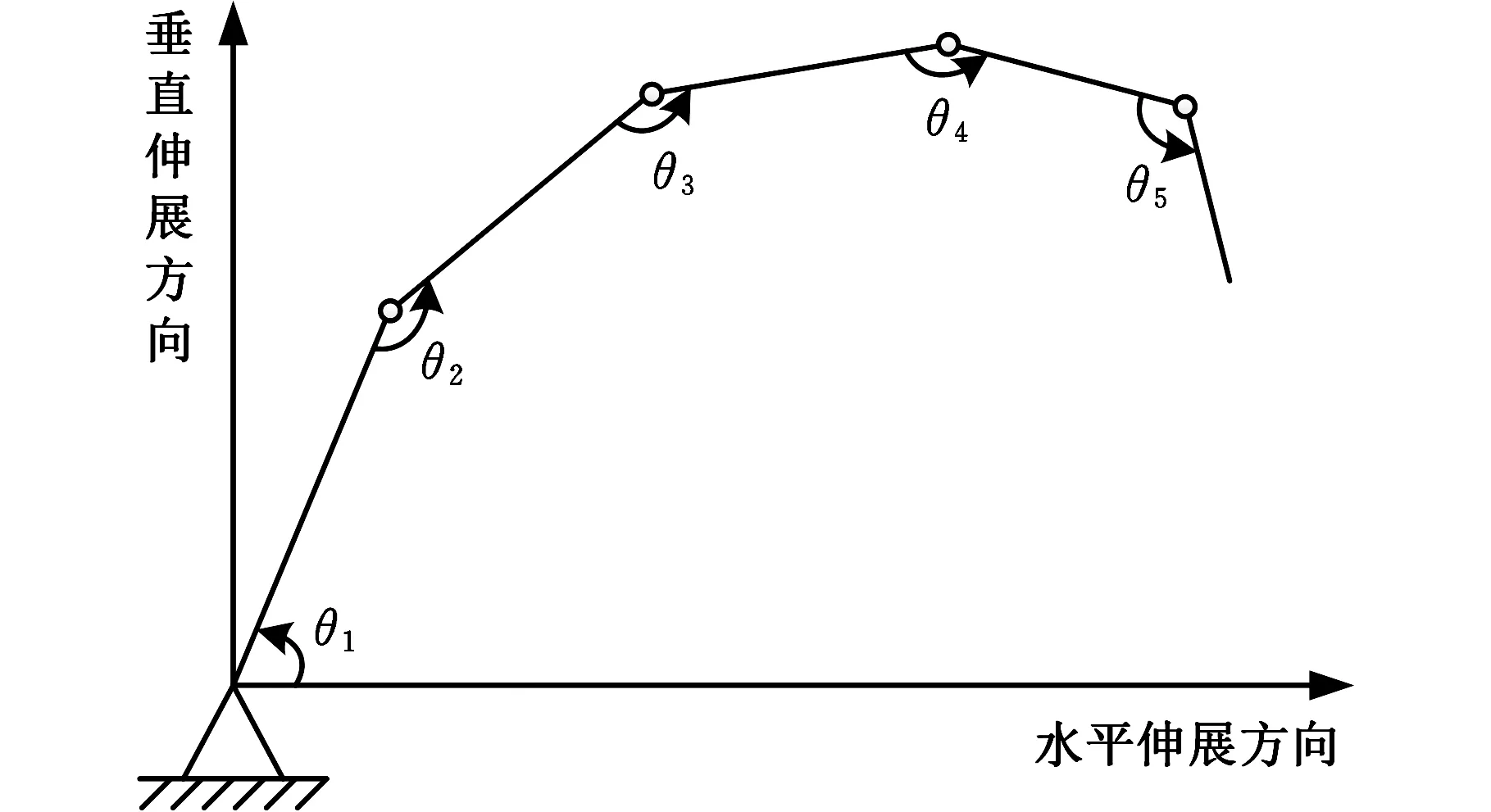
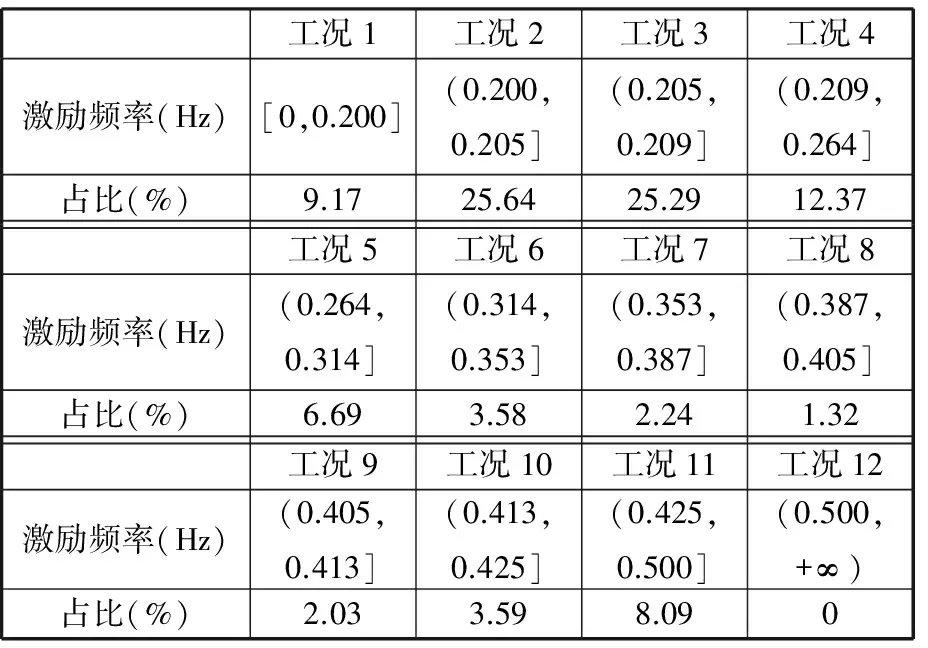
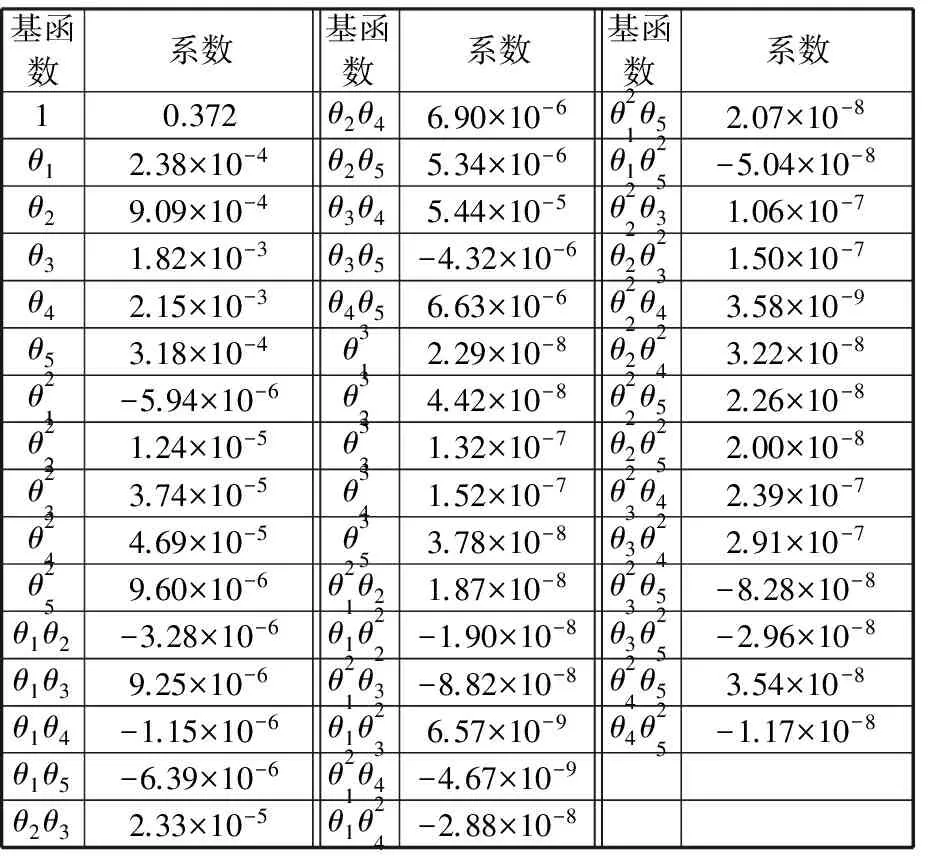
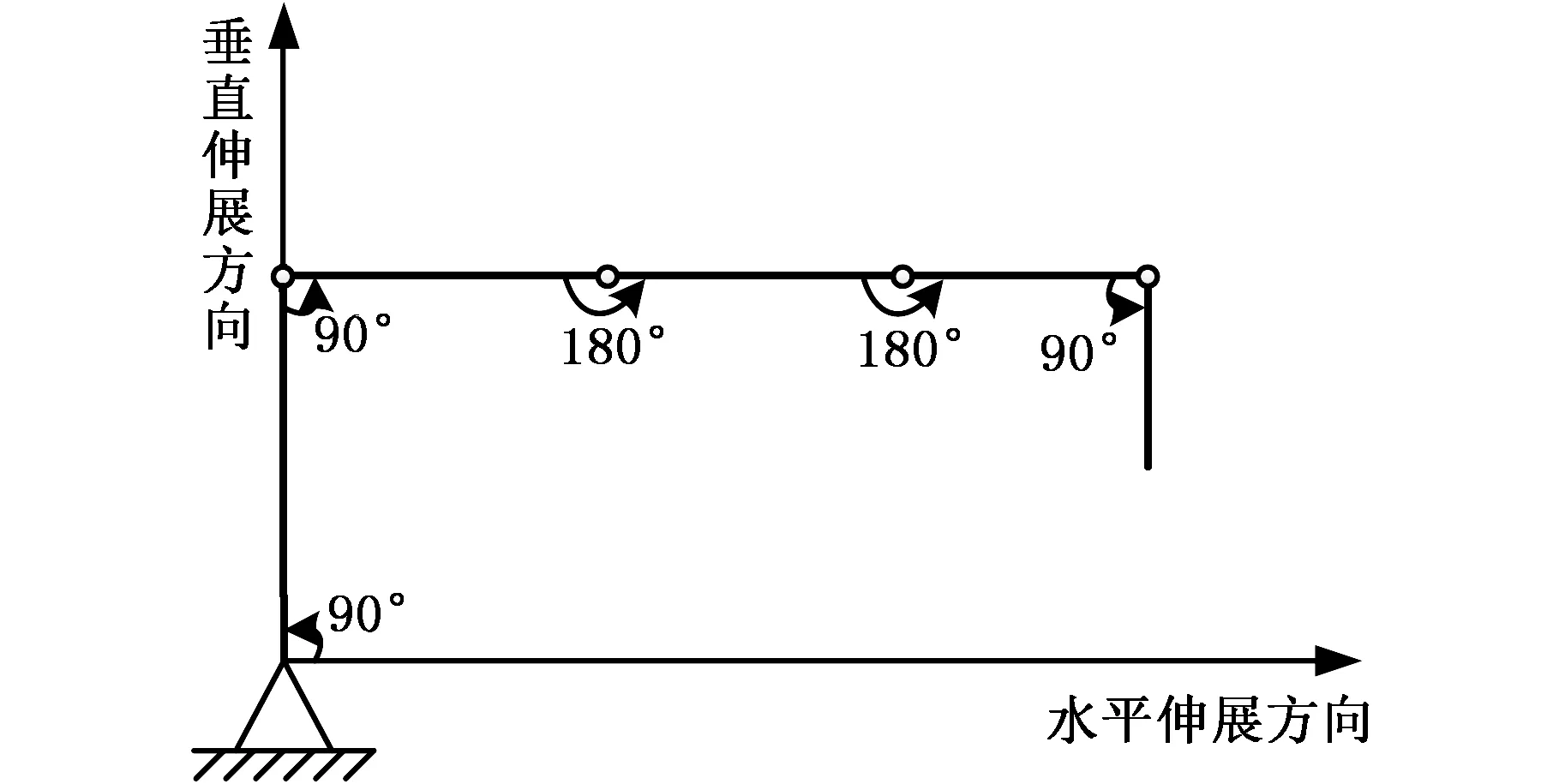
Ωf={fd|fex(1-δ) (1) 式中,fex为激振力频率;δ为频率的错开范围系数。 激振力频率随工况(姿态、挡位等)的变化而变化,根据工程经验数据积累,一般可近似描述为服从某一概率分布的随机变量,因此,对于固有频率为fd的机械臂架结构,其因共振导致结构失效将成为随机事件,共振失效概率即为机械臂架固有频率落入激振频率范围的概率,可表示为 Pf=Pr(fex(1-δ) (2) 式中,Pr()为概率计算函数。 由于上述机械臂共振的失效概率又可表示为 Pf=1-Pr({fd (3) 即 Pf=1-Pr(fd (4) 不妨分别记极限状态函数g1和g2为 (5) 则上述机械臂共振失效概率Pf又可记为 Pf=1-Pr(g1(fd,fex)>0)-Pr(g2(fd,fex)>0) (6) 因此,上述机械臂共振的失效概率可转化为两个单失效模式的可靠性问题,其中机械臂架结构的固有频率fd假设为一确定值,激振力频率fex为一随机变量。此类问题目前已得到大量研究,可通过一阶可靠性方法(first order reliability method,FORM)[8-9]、二阶可靠性方法(second order reliability method,SORM)[10]等方法进行求解。 1.2 机械臂共振的概率-区间混合可靠性分析 在上述分析中,机械臂结构的固有频率fd被考虑为一确定值。然而由于在实际施工环境下,机械臂架的姿态在运行中将随具体任务或施工位置点的改变而变化,因此其固有频率也将发生改变。如图1所示的混凝土泵车,臂架的各姿态角将随浇注点的位置变化而改变,臂架将呈现出多种不同的姿态,因此整个臂架结构的固有频率无法保证在整个施工任务中保持不变,而是随着臂架各姿态角变化而变化的一个变量。机械臂架结构的固有频率关于臂架姿态参数的数学描述可表示为 图1 混凝土泵车臂架结构系统Fig.1 Structural system of booms of the concrete pump truck fd=fd(θ1,θ2,…,θn) (7) (8) (9) 对于该失效概率区间的求解,则需要对结构进行概率-区间混合可靠性分析。 结构可靠性定义为结构在规定的时间内和规定的条件下,完成规定功能的能力。当结构的整体或者某一部分超过某一个特定的状态时,就不能满足预定的功能,这一状态称之为结构的极限状态。设X=(X1,X2,…,Xm)是影响结构功能的m个基本随机变量,Y=(Y1,Y2,…,Yn)为n个区间变量,则结构的极限状态函数可表示为[14] g(X,Y)=0 (10) 当g(X,Y)>0时表示结构可靠,g(X,Y)≤0时表示结构失效。则结构的失效概率可定义为 Pf=Pr{g(X,Y)≤0} (11) (12) (13) 相应地,可靠度指标β也不再是一个定值,而是属于一个区间,即β∈[βL,βU],其中βU和βL分别表示最大和最小可靠度指标。 图2 极限状态带Fig.2 Limit-state zone 基于一阶可靠性方法(FORM)[8-9],求解如下两个优化问题: (14) (15) 可得到极限状态带的最大和最小可靠度指标[11]。其中,U为服从标准正态分布的随机向量,由原空间中的随机变量X=(X1,X2,…,Xm)转换而来。因此,结构的最大和最小失效概率可以表示为 (16) 利用式(14)和式(15)对可靠度指标进行求解涉及一个复杂的两层嵌套优化问题,其中内层为进行区间分析确定功能函数在区间变量上的极值,外层为进行概率分析确定最可能的失效点,通常计算效率极低。为此,本文采用文献[11]提出的解耦方法进行求解,将区间分析嵌入到最可能失效点的寻找过程中,每次迭代过程中依次进行概率分析和区间分析,取得的中间值依次被相互调用,经过多次迭代最终使内外层同时达到稳定解,这样就大大地提高了计算效率。具体迭代过程可参考文献[11,15]。 混凝土泵车臂架的振动主要由混凝土在输送管内的周期性流动冲击载荷所引起,激振力频率一般为0.2~0.4 Hz,并且随工况的变化而变化;而机械臂竖直方向的一阶频率约为0.3~0.4 Hz。当机械臂工作于特定工况、伸展成特定姿态、冲击载荷频率与臂架固有频率接近至一定程度时,臂架就开始剧烈摇晃并导致动应力显著增大。本文将上述方法应用于图1所示的某型实际混凝土泵车多关节柔性臂的振动分析,构建了泵车臂架的混合可靠性分析模型,并通过第2节中的解耦方法对该混合模型进行求解,最终获得了该混凝土泵车臂架在不同工况下的失效概率区间。考虑到机械臂架结构固有频率关于臂架姿态参数的响应分析是基于有限元仿真模型的,单次计算非常耗时,为提高效率,本文基于径向基函数(radial basis function, RBF)[16]构建了固有频率关于姿态参数的精确代理模型,避免了仿真模型的不断调用,极大地提高了上述混合可靠性问题的求解效率。 3.1 径向基函数代理模型 代理模型方法的主要思想就是通过构造一个计算量小但计算结果与仿真分析相近的数学模型来“代理”仿真分析模型。常用的代理模型主要有多项式响应面模型、Kriging模型、径向基函数模型、人工神经网络模型等。径向基函数是一种灵活性好、结构简单、计算量相对较少的代理模型,具有许多优异的数学特性,被广泛用于偏微分方程求解、地球物理、测绘测量、遥感与信息处理等领域[17-18]。径向基函数是以径向函数为基函数,通过线性叠加构造出来的模型,其基本形式如下: (17) 式中,wi为线性叠加系数;φi(r)为径向函数;ns为样本点个数。 径向函数是以样本点为中心,以预测点x与样本点x(i)之间的欧氏距离为自变量的一类函数,表示如下: φi(r)=φ(‖x-x(i)‖) (18) 通过不同的线性叠加系数wi,RBF能够近似不同的响应函数。常用的径向基函数见表1,其中c为形状参数,σ为标准差,r=‖x-x(i)‖为Euclidean范数。 表1 常用的径向基函数 3.2 泵车臂架混合可靠性分析流程 综合上述分析,将基于径向基函数代理模型的混凝土泵车柔性机械臂架振动混合可靠性分析具体流程归纳如下: (1)在柔性机械臂可变构型范围空间内,建立振动可靠性分析中动力学特性变量(例如结构固有频率fd)关于构型不确定性参量θ=(θ1,θ2,…,θn)的代理模型。①建立柔性机械臂架动力学模型。柔性机械臂架的动力学建模方法很多,有限元法是一种比较成熟的建模方法,适用于多种柔性机械臂结构。②试验设计。将构型不确定性参量θ=(θ1,θ2,…,θn)视为试验设计的因素,根据因素个数和各因素的限制变化范围确定水平数,选择合适的抽样方法进行抽样。③构造合适的代理模型。对所选样本点进行试验,并根据试验所得的样本数据,采用合适的响应面模型构造动力学特性变量fd关于构型不确定参量θ的近似响应函数: fd=fd(θ)=fd(θ1,θ2,…,θn) (19) 并对其近似能力进行验证。 (2)基于步骤(1)建立的构型-动力学特性响应面函数,结合激励载荷情况,建立概率-区间混合可靠性分析模型,并求解。①确定功能函数。根据外载荷L、系统动力学特性fd和振动状态变量的允许值,确定柔性机械臂振动问题的功能函数如下: Z=g(L,f)=g(L,θ1,θ2,…,θ5) (20) 3.3 结果分析 按泵车臂架的设计要求,本文中频率的错开范围系数取δ=0.05。选择图3所示的各关节位置臂节间的夹角θ1、θ2、θ3、θ4、θ5为区间变量。根据工程经验数据积累,获得激振力频率的工程统计分布如表2所示。根据该统计分布特征,本文将激振力频率处理为随机变量,并采用Weibull分布对激振力频率进行拟合,获得随机变量的相关参数。 图3 混凝土泵车臂架姿态角Fig.3 Attitude angles between booms of the concrete pump truck 表2 关于激振力频率的工程统计分布 Weibull分布的概率密度函数表达形式如下: (21) 其中,根据样本统计信息估计得到比例参数λ=0.2765,形状参数k=2.7598。表3所示为该泵车臂架共振分析所考虑的主要不确定变量及其概率/非概率特征参数。 表3 泵车臂架共振问题不确定变量Tab.3 Uncertain variables involved in the resonance vibration of the boom of pump truck 由于混凝土泵车臂架工况环境复杂,在实际工程中通常难以得到臂架机械臂固有频率fd与不确定变量间的显式函数表达式,本文拟通过有限元仿真获得臂架振动构型样本数据,并建立响应面进行拟合以对实际响应函数进行近似。图4为某型混凝土泵车臂架的有限元频率分析模型,本文根据5种臂架构型的模态频率试验数据修正了有限元模型,通过均匀采样得到100个臂架构型样本点进行有限元分析,建立径向基函数形式的代理模型对臂架的固有频率进行近似估计,并通过多个验证点校核模型的精度。表4所示为构建的径向基函数的基函数及相应的系数。 图4 某型混凝土泵车臂架有限元频率分析模型Fig.4 Finite element analysis model for frequencies of booms of a concrete pump truck 表4 泵车臂架竖直方向一阶固有频率的响应面模型 通过对泵车臂架不确定参数进行概率/区间度量,并构建径向基函数对实际臂架振动固有频率关于以上不确定参数的函数关系进行近似,即可基于概率-区间混合可靠性分析技术对泵车臂架的共振问题进行可靠性求解。通过计算求得泵车臂架在不同工况下的失效概率为Pf∈[4.71%,50.44%]。结果表明,在不同工况下,至少存在某一种工况,使得在该工况下臂架的失效概率可达到50.44%。致使臂架失效概率达到最大值50.44%的姿态及其姿态角情况如图5所示。在实际施工过程中,应当避免使混凝土泵车臂架构成或接近此种姿态,以防结构破坏失效。而如果完全基于传统概率可靠性分析,在信息量不足的情况下将多关节柔性机械臂关节夹角在[0°, 90°]或[90°, 180°]内视为均匀分布,计算可得该臂架在不同工况下的综合失效概率仅为5.03%,这一结果因没有考虑到泵车臂架在某些极端工况下的最不利因素,导致对臂架可靠度的判断错误。因此,对工程机械臂架进行混合可靠性分析有助于臂架系统在各施工工况下结构的可靠性估计,使得在设计阶段对结构的可靠性状况了解更为全面,避免因误判导致实际施工过程中发生结构失效。 图5 最大失效概率(50.44%)所对应的臂架姿态Fig.5 The boom gesture case of the maximum failure probability (50.44%) 针对柔性机械臂架振动可靠性分析中臂架动力学特性多变、部分构型参数难以精确度量、仿真分析计算量大等特点,本文提出了基于径向基函数响应面的柔性机械臂架混合可靠性分析方法。通过构建柔性机械臂架结构振动失效的混合可靠性模型,对臂架结构的振动失效概率区间进行了估计。通过结果分析我们发现,对区间变量作不合理的概率假设,可导致对臂架结构实际可靠度的严重错误判断。因此,在参数信息缺乏的情况下,混合可靠性分析方法可为结构的可靠性分析提供一个合理的失效概率区间(而非一确定的数值),将有助于实际工程机械臂架的安全设计,为柔性机械臂架结构系统的可靠运行提供保障。 [1] 陈世基, 于霖智. 智能机器人机械臂动态可靠性粗糙-模糊综合评价研究[J]. 计算机测量与控制,2010,18(1):139-141. CHEN Shiji, YU Linzhi. Research on Synthesis Assessment of Intelligence Robot Arm Dynamic Reliability Based on RS -FS[J]. Computer Measurement & Control,2010,18(1):139-141. [2] 赵宽, 陈建军, 曹鸿钧, 等. 随机参数双连杆柔性机械臂的可靠性分析[J]. 工程力学,2015,32(2):214-220. ZHAO Kuan, CHEN Jianjun, CAO Hongjun, et al. Reliability Analysis on Two-link Flexible Robot Manipulator with Random Parameters[J]. Engineering Mechanics,2015,32(2):214-220. [3] 杨峰. 机器人机械臂模态分析及可靠性分析[D]. 南京: 南京理工大学, 2013. YANG Feng. Modal Analysis and Reliability Analysis of Robotic Manipulator[D]. Nanjing: Nanjing University of Science and Technology,2013. [4] RAO S S, BHATTI P K. Probabilistic Approach to Manipulator Kinematics and Dynamics[J]. Reliability Engineering and System Safety,2001,72(1):47-58. [5] KOTOSAKA S, TAKATA S, KOHDA T, et al. Reliability Evaluation of Manipulators by Means of Probability of Task Achievement[J]. Journal of the Japan Society for Precision Engineering, 1995,61(5):717-721. [6] LI T, JIA Q X, CHEN G, et al. Kinematics Reliability Analysis for Manipulator Considering Elasticity [C]// IEEE 9th Conference on Industrial Electronics and Applications (ICIEA). Hangzhou,2014:1633-1638. [7] BEN-HAIM Y, ELISHAKOFF I. Convex Models of Uncertainties in Applied Mechanics[M]. Amsterdam: Elsevier Science Publisher,1990. [8] HASOFERA M, LIND N C. Exact and Invariant Second-moment Code Format[J]. ASME Journal of the Engineering Mechanics Division,1974,100:111-121. [9] RACKWITZ R, FIESSLER B. Structural Reliability under Combined Random Load Sequences[J]. Computers & Structures,1978,9(5):489-494. [10] BREITUNGK W. Asymptotic Approximation for Probability Integrals[J]. Probabilistic Engineering Mechanics,1989,4(4):187-190. [11] DU X P. Interval Reliability Analysis [C]// ASME 2007 International Design Engineering Technical Conference & Computers and Information in Engineering Conference (IDETC2007). Las Vegas,2007:1103-1109. [12] LUO Y J, KANG Z, ALEX L. Structural Reliability Assessment Based on Probability and Convex Set Mixed Model[J]. Computers & Structures,2009,87:1408-1415. [13] JIANG C, LI W X, HAN X, et al. Structural Reliability Analysis Based on Random Distributions with Interval Parameters[J]. Computers & Structures,2011,89:2292-2302. [14] JIANG C, LU G Y, HAN X, et al. A New Reliability Analysis Method for Uncertain Structures with Random and Interval Variables[J]. International Journal of Mechanics and Materials in Design,2012,8(2):169-182. [15] 刘丽新. 基于概率与非概率凸集的混合可靠性分析方法研究[D]. 长沙:湖南大学,2012. LIU Lixin. Hybrid Reliability Analysis Method Based on Probabilistic and Non-probabilistic Convex Model[D]. Changsha: Hunan University,2012. [16] BUHMANNM D. Radial Basis Functions: Theory and Implementations[M]. Cambridge: Cambridge University Press,2003. [17] FRANK R, SCHABACK R. Solving Partial Differential Equations by Collocation Using Radial Basis Functions[J]. Applied Mathematics and Computation,1998,93(1):73-82. [18] HARDY R L. Multiquadric Equations of Topography and Other Irregular Surfaces[J]. Journal of Geophysical Research,1971,8:1905-1915. (编辑 王艳丽) Hybrid Reliability Analysis for Flexible Manipulator Vibrations in Engineering Machinery ZENG Guang1, 2JIANG Chao1NI Bingyu1 1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University, Changsha,410082 2.Zoomlion Heavy Industry Science and Technology Co., Ltd., Changsha,410013 Based on the probabilistic and interval hybrid model and structural reliability analysis method, vibration reliability analyses for engineering mechanical systems with multi-joint flexible manipulators was investigated. According to different types of the uncertain parameters in mechanical manipulators, the uncertainties were quantified by random and interval variables. With simulation data of finite element model, a RBF agent model was built for structural natural frequencies with regard to mechanical manipulator’s parameters. And the failure probability of the mechanical manipulators due to resonance was evaluated based on the probabilistic and interval hybrid reliability analysis method. Finally the above analysis method was applied for a practical project example to make an illustration. flexible manipulator; vibration analysis; probabilistic and interval hybrid model; radial basis function(RBF) agent model 2016-04-15 国家自然科学基金资助项目(11172096,51222502) TB114.3 10.3969/j.issn.1004-132X.2017.12.003 曾 光,男,1983年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生,中联重科股份有限公司中央研究院工程师。研究方向为工程机械结构的可靠性。姜 潮,男,1978年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。倪冰雨(通信作者),男,1989年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。E-mail:nby@hnu.edu.cn。
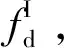

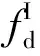

2 概率-区间混合可靠性分析方法

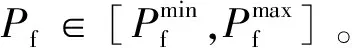
3 工程应用

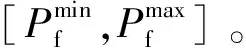

4 结论

