迈步过程接触刚度变化对超前支架动态响应影响分析

谢 苗 刘治翔 毛 君辽宁工程大学机械工程学院,阜新,123000



迈步过程接触刚度变化对超前支架动态响应影响分析

谢 苗 刘治翔 毛 君辽宁
工程大学机械工程学院,阜新,123000

通过数值仿真和实验方法对超前支架迈步过程的动态响应特性进行研究。使用块系覆岩理论构造超前支架与顶板的耦合动力学模型。以超前支架与顶板接触刚度变化模拟超前支架的迈步过程。将超前支架迈步过程与顶部接触刚度设定为阶跃突变方式、指数型、直线型和对数型方式进行变化，研究此过程顶板、第一和第二支撑组的动态响应。使用MATLAB建立超前支架迈步过程动力学微分方程，并使用四阶龙格库塔计算方法对超前支架迈步过程的动力学问题进行求解。仿真和实验结果表明，使用阶跃突变方式进行支架迈步过程接触刚度的控制时，会引起顶板和各个支撑组的剧烈振动。使用对数型、直线型和指数型刚度变化方式进行迈步过程控制，能够减小顶板、第一和第二支撑组的振动量，并且三种方式减小振动量的效果逐渐递增。

超前支架；接触刚度；动态响应；迈步过程

0 引言

传统的巷道支护材料与支护结构已不能满足复杂条件下巷道支护要求，在巷道掘进成巷作业中，采用传统支护方式所需的时间约占总作业时间的70%，且支护作业人员众多，劳动强度过大，耗时长，效率低，安全性差。研究更加合理和实用的巷道支护理论对促进综掘自动化的发展进程显得尤为重要。超前支护属于综掘工作面的一种临时支护设备，可以及时支护掘进工作面巷道围岩；保护掘进施工人员的安全；与掘进设备和锚固设备配套使用，实现掘、支、锚成套装备平行作业；在较大程度上增加掘进时间的同时有效降低非掘进时间，提高工作效率的同时也提高了综掘工作的安全性[1-2]。近年来，随着煤矿行业的发展以及人们对煤矿安全开采意识的增强，超前支架技术得到广泛关注。

文献[3-5]针对综掘巷道超前支架与围岩相互作用机理以及超前支架结构设计和强度校核等进行了基础研究并进行了静动力学特性分析。文献[6]使用模糊PID控制算法对超前支架的支撑力自动控制进行了研究。文献[7] 以顶板扰动量最小为控制目标，针对超前支架在迈步过渡过程的支撑力控制系统进行了研究。文献[8]以超前支架升降过程效率和顶板扰动量最小为控制目标，针对超前支架的电液伺服位置和压力复合控制方法进行了研究。文献[9]针对超前支架多缸同步控制方法进行了研究。

超前支架迈步过程，即超前支架从双组支撑状态过渡到单组支撑状态，再由单组支撑状态过渡到双组支撑状态时，是超前支架最不稳定且对顶板扰动最大的时刻。目前，针对此过程中超前支架的动力响应特性的研究很少。本文主要研究超前支架迈步过程以及超前支架和顶板耦合体系的动力响应特性。

1 超前支架结构

超前支架结构如图1所示，迈步式超前支架由主副支撑组、推移机构等组成，支撑组的主要组成部件有纵梁、横梁、顶部阻尼体、各类千斤顶、立柱组等，支撑纵梁均布安装在横梁上，以超前支架的中轴线为轴对称布置且与巷道轴向平行。超前支架骑跨在掘进机上方，能够跟随掘进机的推进迈步前进。

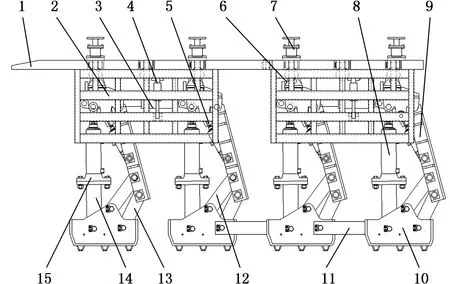
1.纵梁 2.侧护板 3.推移油缸 4.侧推油缸 5.平衡千斤顶 6.横梁 7.顶部阻尼体 8.副支撑组 9.掩护梁 10.底座 11.导向板 12.前连杆 13.后连杆 14.立柱 15.主支撑组图1 超前支架结构Fig.1 Structure of advanced support

2 超前支架与顶板耦合动力学模型

本文使用块系覆岩理论构造超前支架与顶板的耦合动力学模型，如图2所示。假设巷道顶部由n个块系覆岩组成，质量为mi(i=1,2,…,n)，岩石相对于岩石间松软结构刚度较大，因此视为刚体。岩石间松软结构视为黏弹性凯尔文体，弹性系数为ki，阻尼系数为ci(i=1,2,…,n)。kn1和cn1是超前支架第一支撑组与顶板岩石的接触刚度和阻尼，kn2和cn2是超前支架第二支撑组与顶板岩石的接触刚度和阻尼，ms1为超前支架第一支撑组的等效质量，ms2为超前支架第二支撑组的等效质量[10-11]。

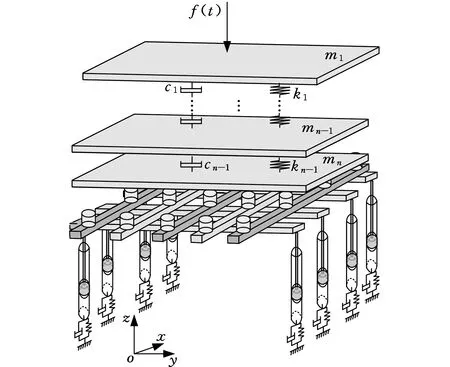
(a)三维立体模型

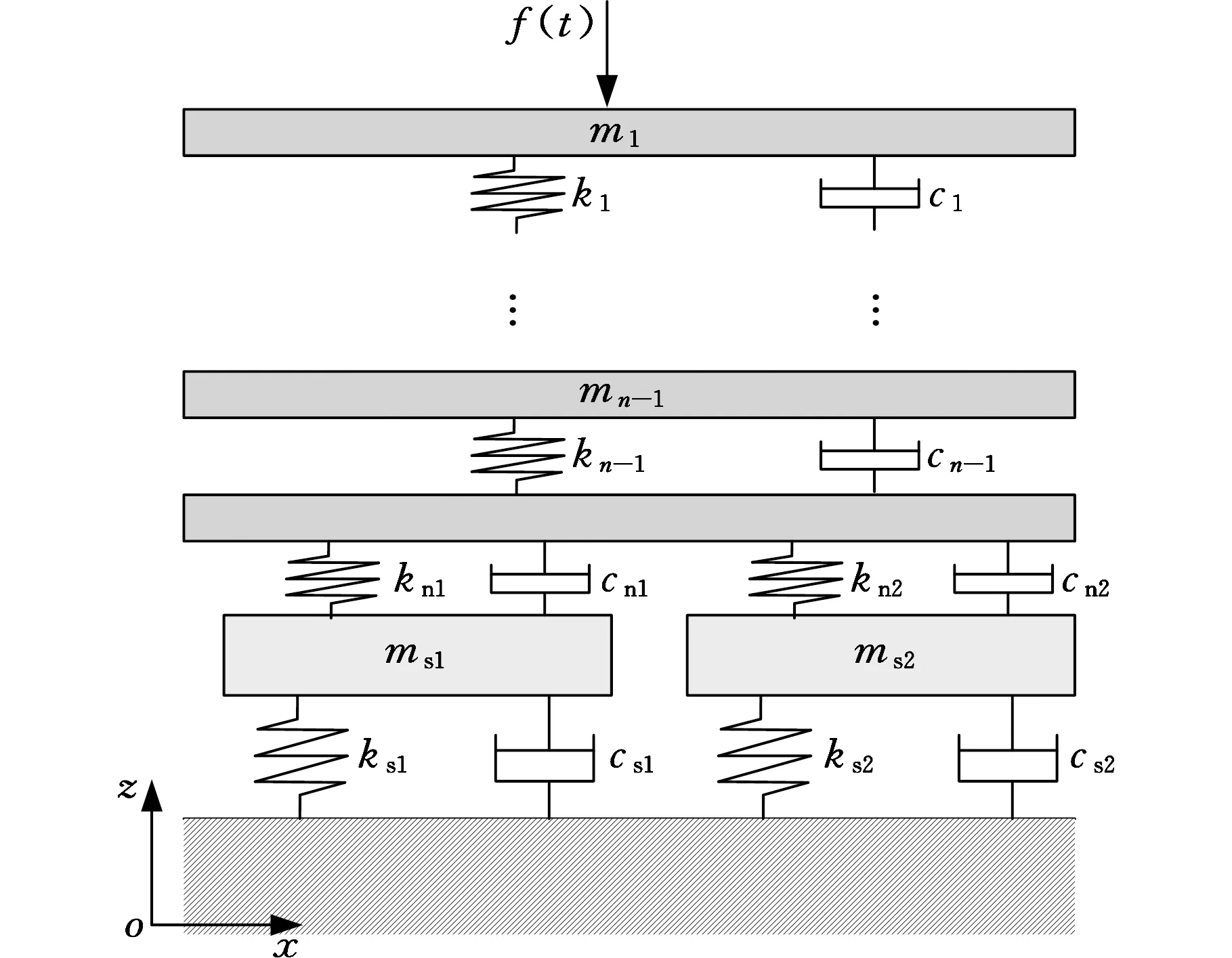
(b)二维简化模型图2 顶板与支护理论模型Fig.2 Supporting theory model of advanced supporting head-on roadway

假设扰动作用力为f(t)，超前支架的第一支撑组和第二支撑组之间的振动互不干扰，耦合体系动力学模型的坐标原点为岩石体系的静平衡位置。可以得到超前支架与顶板耦合动力响应微分方程：

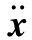
(1)

式中，M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x为位移向量；F(t)为外载荷向量；δ为由各质量块重力引起位移量的矩阵。

由静力平衡可得

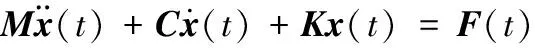
(2)

以微分方程形式表示为

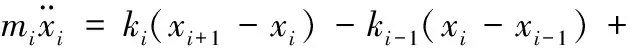
(3)

其中，i=1,2,…,n-1。F1=A1sinω1t，表示外载荷由一正弦激励简化得到。

3 超前支架迈步过程动态响应仿真

本文将超前支架迈步过程看作是超前支架各个支撑组与顶板接触刚度变化的过程。第一支撑组迈步时，首先支撑组下降，脱离顶板，此时第一支撑组与顶板的接触刚度由原来稳定值变为0；然后第一支撑组向前推移10 s；支撑组上升，直至与顶板接触完成支撑，此时第一支撑组与顶板的接触刚度由0变为初始值，之后第二支撑组下降，如此往复循环。

使用MATLAB建立超前支架-顶板耦合体系动力学微分方程组，并使用龙格-库塔数值方法求解微分方程组。超前支架-顶板耦合体系动力学模型中岩石层参数设置如下：n=9，mi=1000 kg，ki=2 MN/m，ci=200 N·s/m，i=0，1，…，9，其中k9为总接触刚度；超前支架的质量ms1=ms2=2000 kg，超前支架刚度ks=500 kN/m，阻尼cs=200 N·s/m。

3.1 接触刚度的阶跃突变

设定第一支撑组与顶板接触刚度以阶跃突变方式在0.1 s内由500 kN/m变为0，通过仿真得到这一过程中顶板、第一支撑组和第二支撑组的动态响应，如图3所示。

仿真结果表明:①支架迈步过程中，第一支撑组下降前，顶板、第一支撑组和第二支撑组的振动位移幅度分别为27 mm、23 mm和23 mm；②第一支撑组下降后，顶板、第一支撑组和第二支撑组的振动位移幅度分别为46 mm、0和46 mm；③第一支撑组上升支撑后，顶板、第一支撑组和第二支撑组的振动位移幅度恢复到下降前的状态；④第一支撑组下降时，顶板和第二支撑组的振动位移最大值分别为28 mm、-24 mm和25 mm、-23 mm；⑤第一支撑组上升时，顶板、第一支撑组和第二支撑组的振动位移最大值分别为23 mm、-27 mm，21 mm、-22 mm和22 mm、-26 mm。

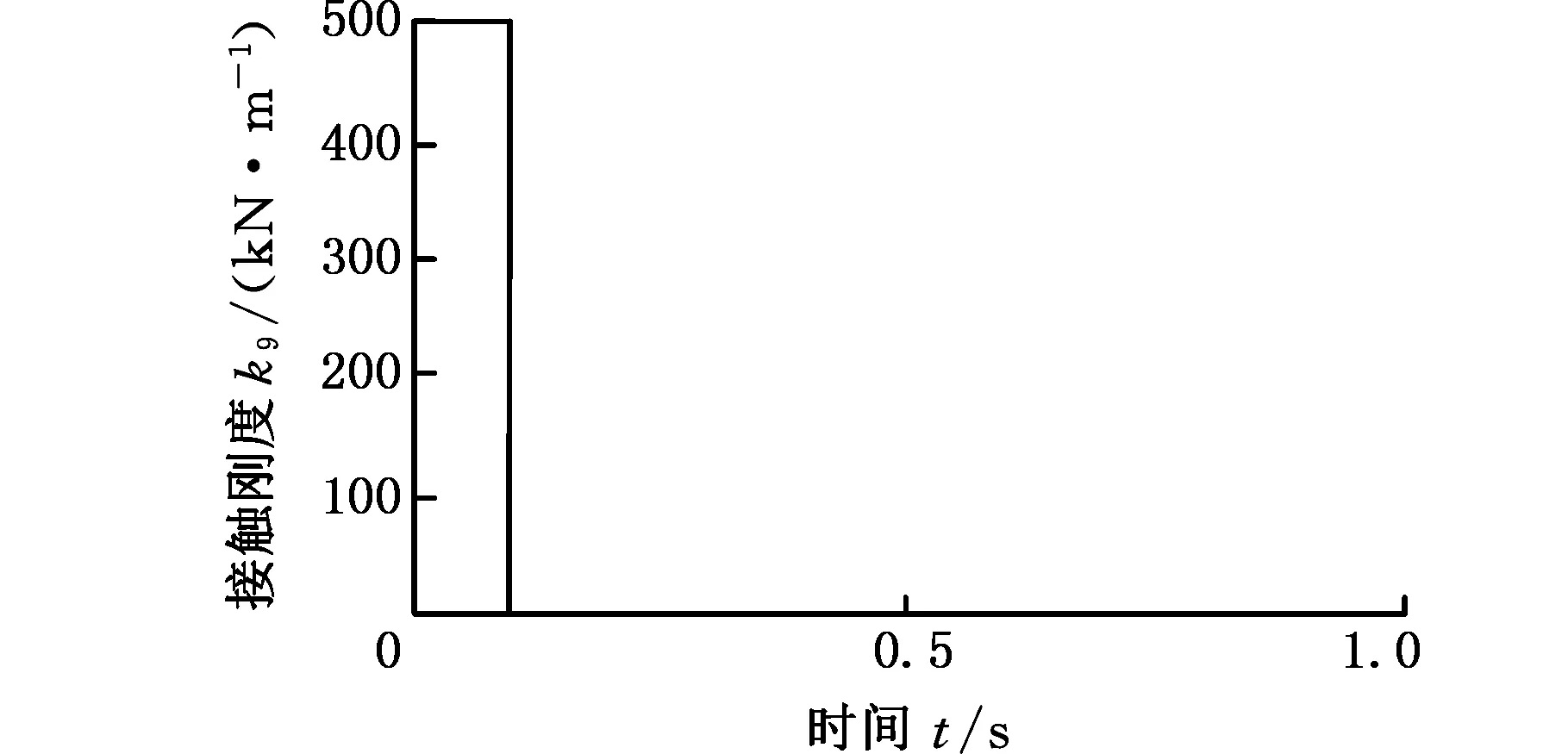
(a)接触刚度变化给定曲线

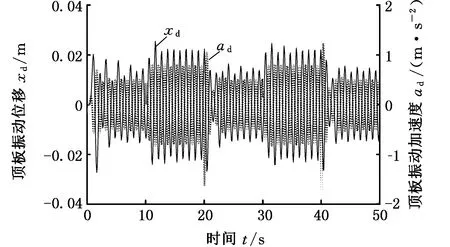
(b)顶板振动位移和振动加速度

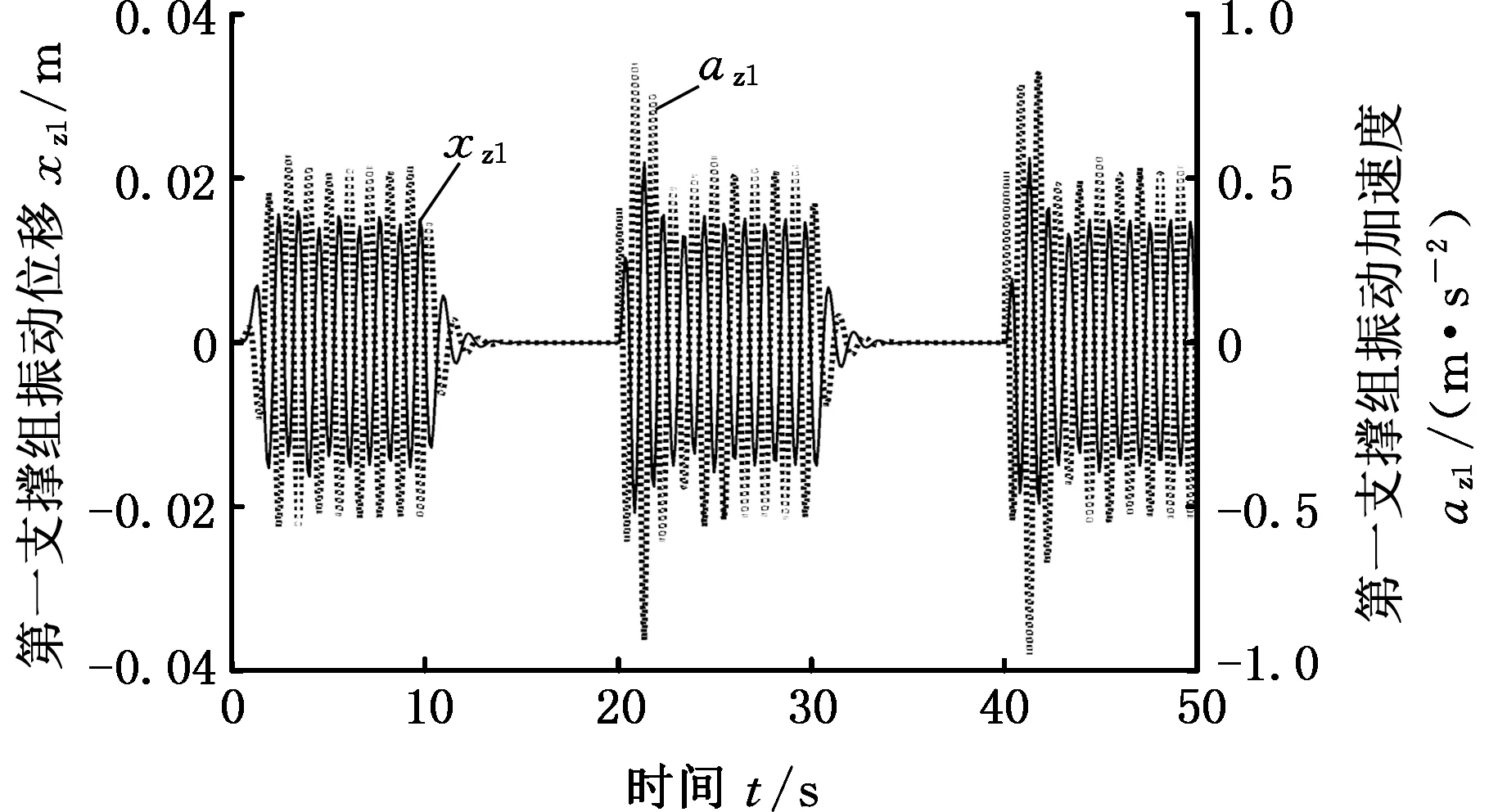
(c)第一支撑组振动位移和振动加速度

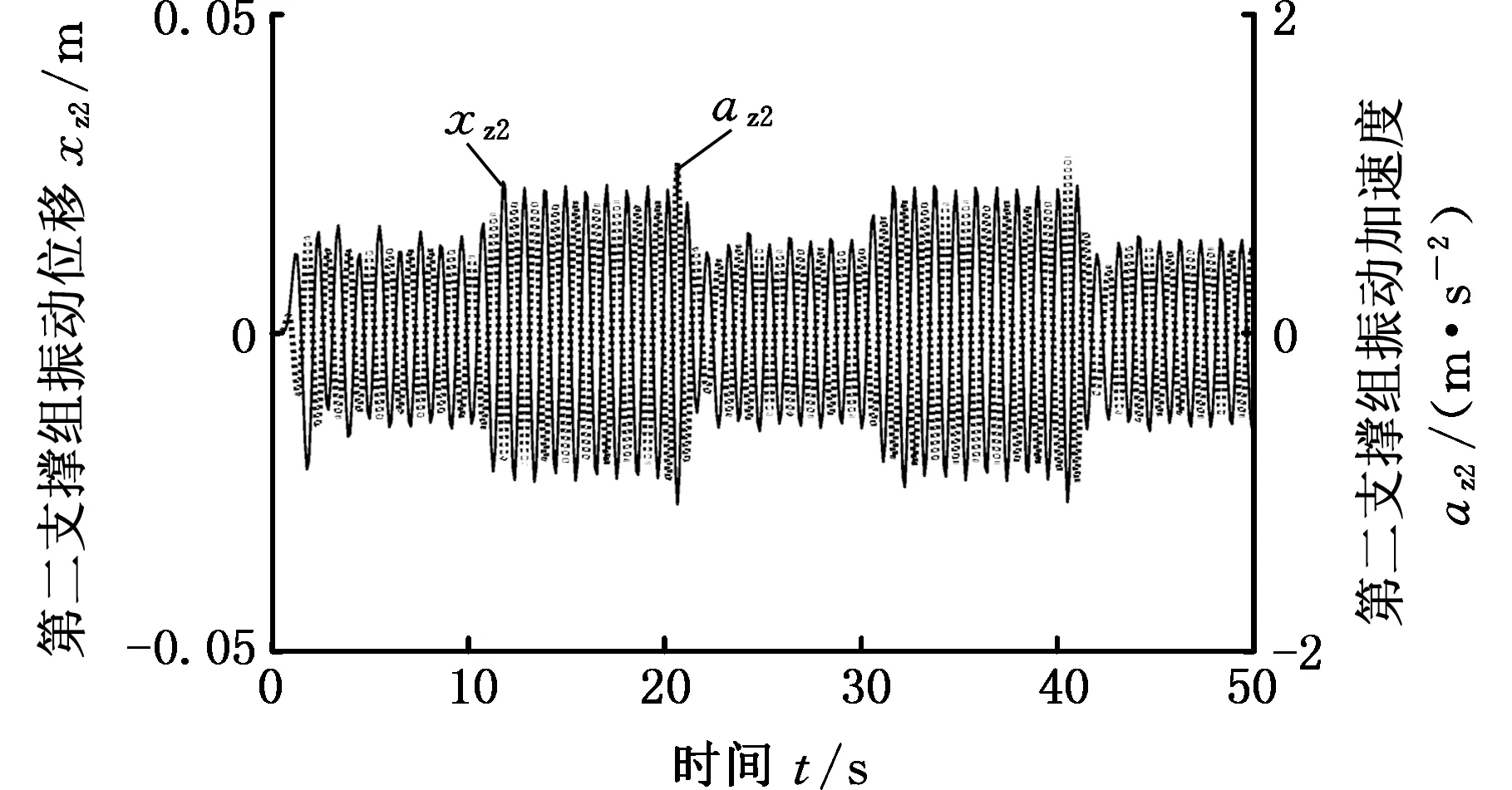
(d)第二支撑组振动位移和振动加速度图3 接触刚度阶跃突变的仿真结果Fig.3 Simulation results of contact stiffness step mutation

在第一支撑组下降和上升时，引起顶板和第二支撑组的振动较为剧烈，因此本文对第一支撑组下降和上升使用不同速度，以减小顶板和第二支撑组的振动幅度。

3.2 接触刚度的对数型变化

设定第一支撑组与顶板接触刚度以对数曲线方式在1.0 s内由500 kN/m变为0，通过仿真得到这一过程中顶板、第一支撑组和第二支撑组的动态响应，如图4所示。

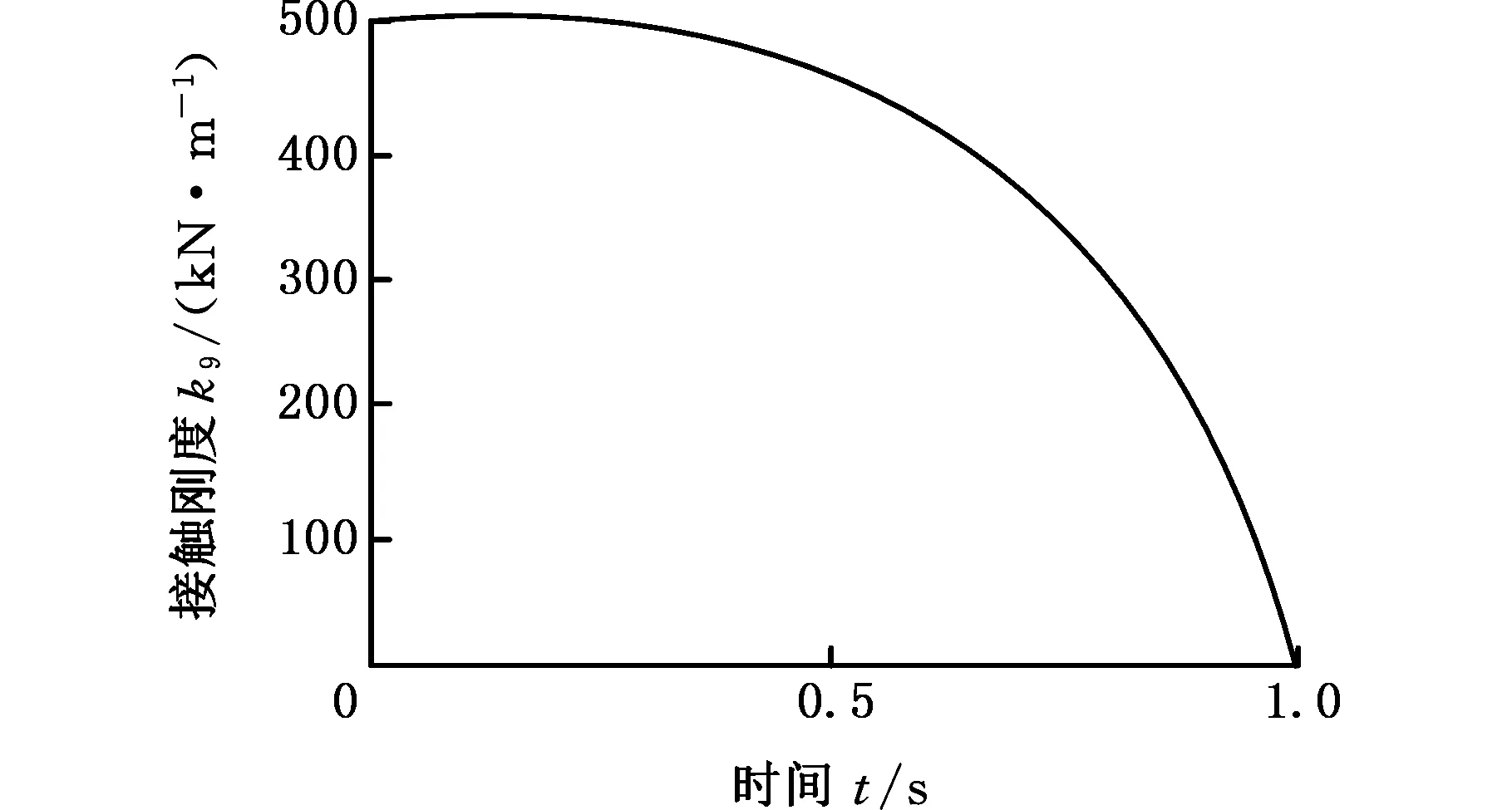
(a)接触刚度变化给定曲线

(b)顶板振动位移和振动加速度

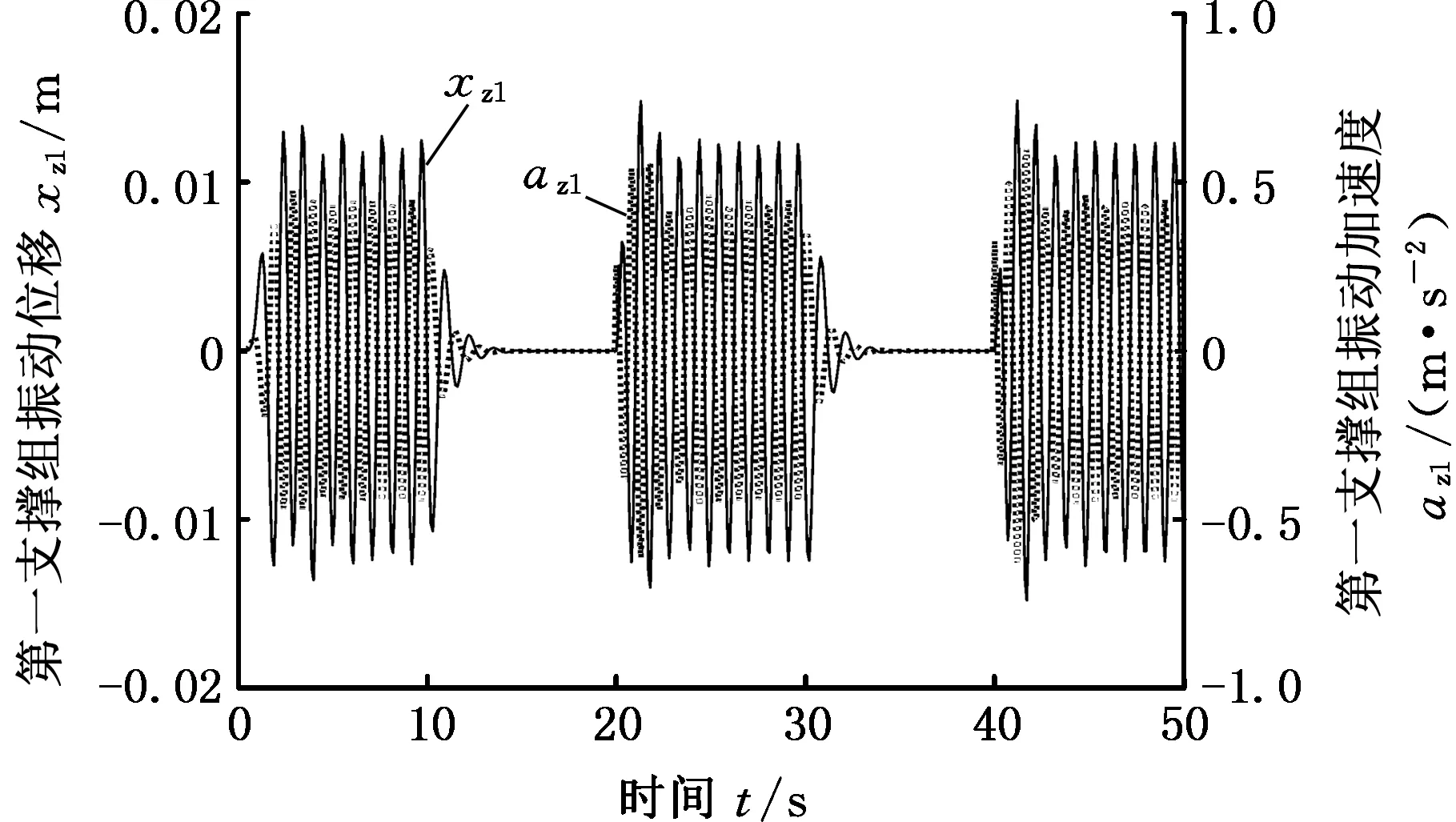
(c)第一支撑组振动位移和振动加速度

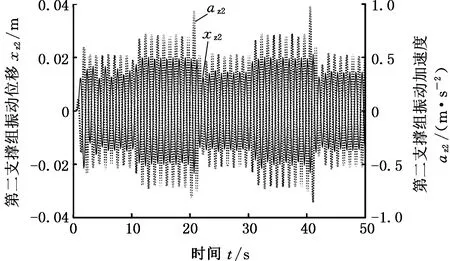
(d)第二支撑组振动位移和振动加速度图4 接触刚度对数变化的仿真结果Fig.4 Simulation results of contact stiffness exponential

仿真结果表明：①支架迈步过程中，第一支撑组下降前，顶板、第一支撑组和第二支撑组的振动位移幅度分别为27 mm、23 mm和23 mm；②第一支撑组下降后，顶板、第一支撑组和第二支撑组的振动位移幅度分别为45 mm、0和44 mm；③第一支撑组上升支撑后，顶板、第一支撑组和第二支撑组的振动位移幅度恢复到下降前的状态;④第一支撑组下降时刻，顶板和第二支撑组的振动位移最大值分别为25 mm、-22 mm和21 mm、-21 mm；⑤第一支撑组上升时刻，顶板、第一支撑组和第二支撑组的振动位移最大值分别为21 mm、-23 mm，19 mm、-18 mm和19 mm、-22 mm。

3.3 接触刚度的直线型变化

设定第一支撑组与顶板接触刚度以直线方式在1.0 s内由500 kN/m变为0，通过仿真得到这一过程中顶板、第一支撑组和第二支撑组的动态响应，如图5所示。

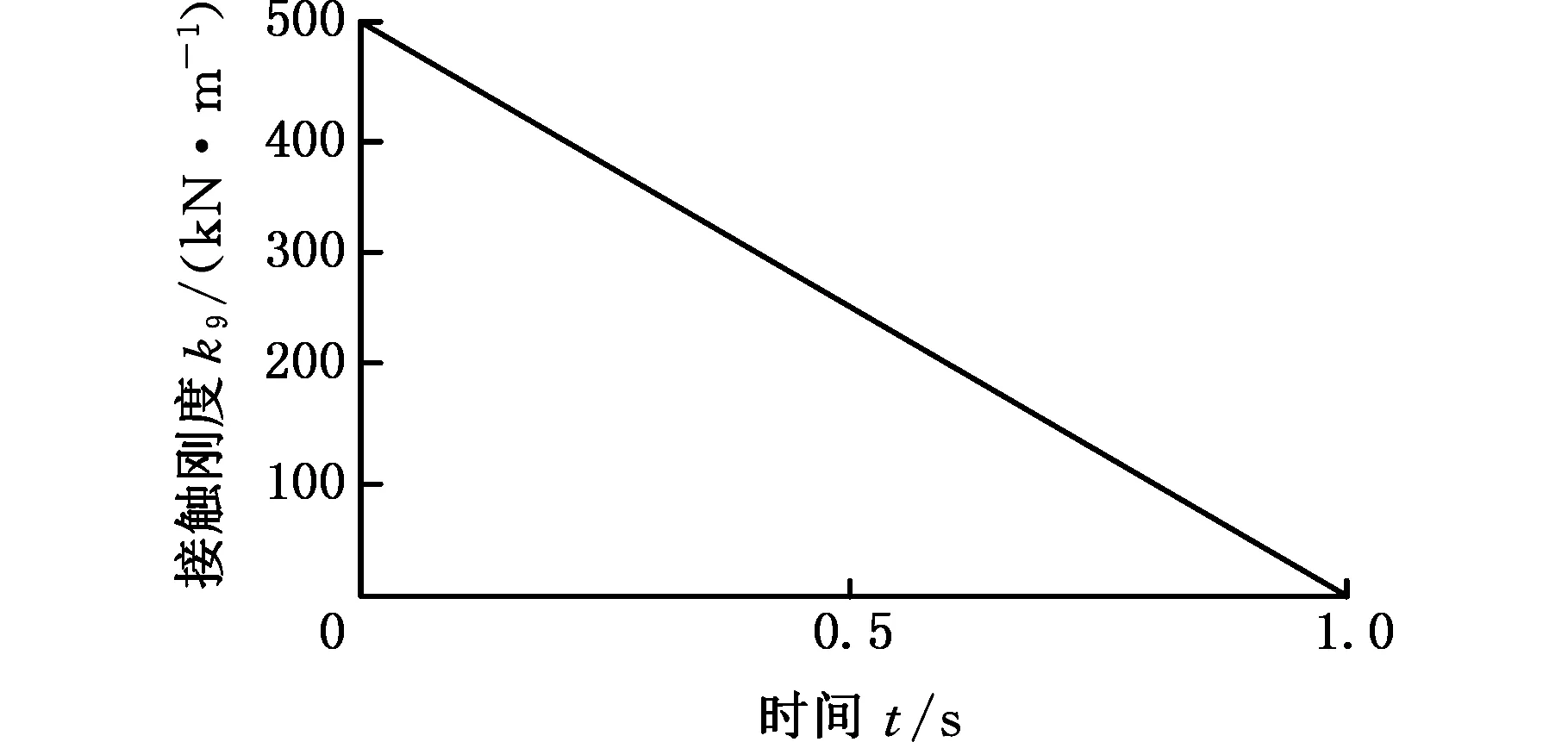
(a)接触刚度变化给定曲线

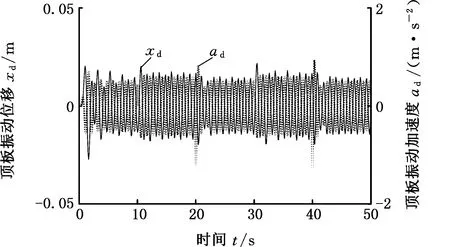
(b)顶板振动位移和振动加速度

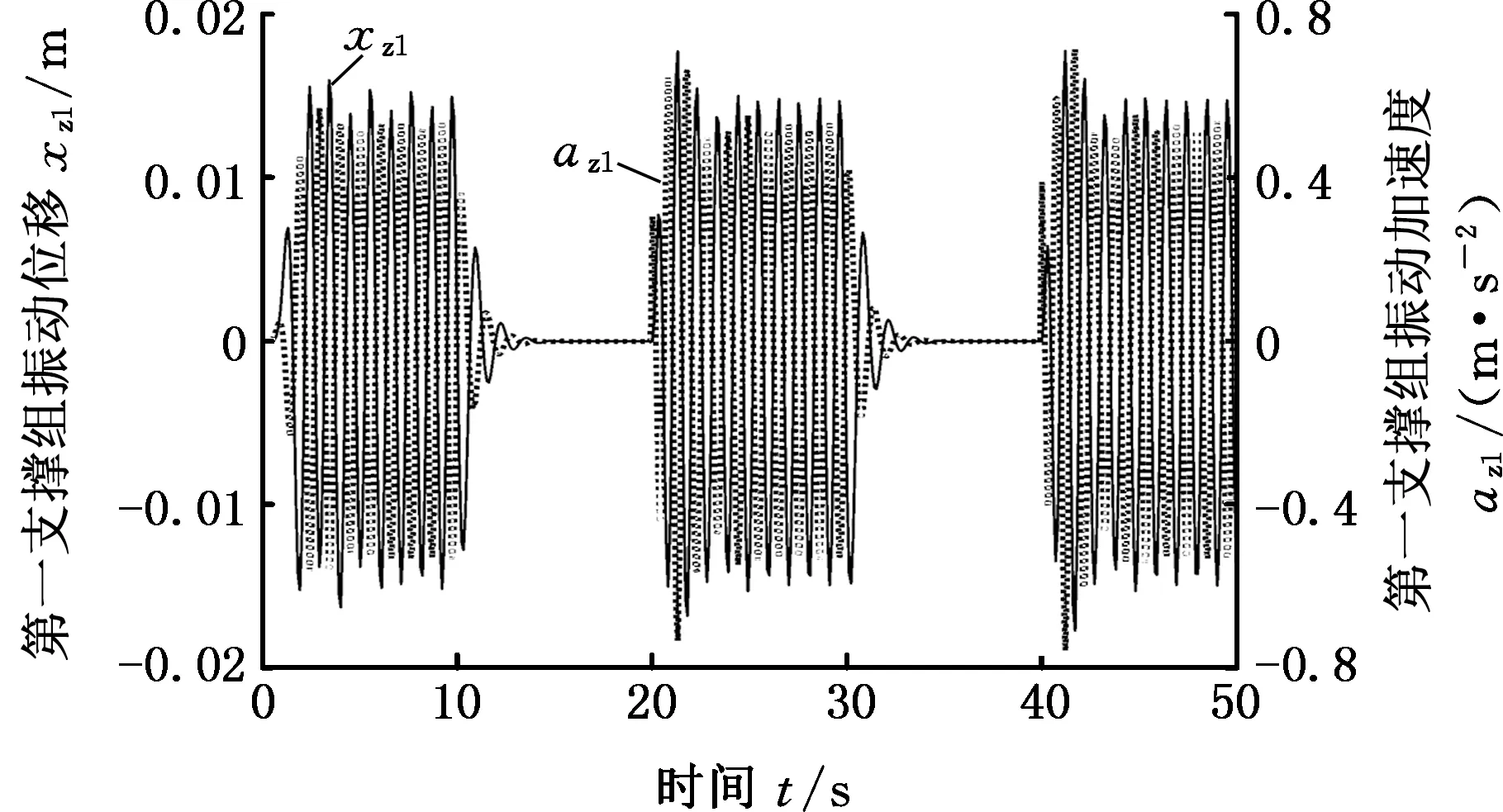
(c)第一支撑组振动位移和振动加速度

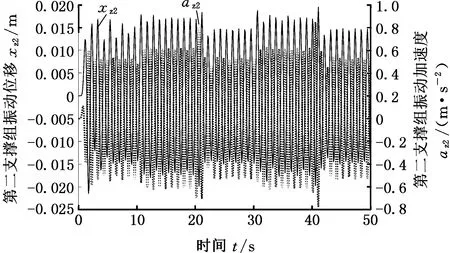
(d)第二支撑组振动位移和振动加速度图5 接触刚度直线变化的仿真结果Fig.5 Simulation results of contact stiffness linear

仿真结果表明，第一支撑组下降时刻，顶板和第二支撑组的振动位移量最大值分别为18 mm、-17 mm和17 mm、-18 mm；第一支撑组上升时刻，顶板、第一支撑组和第二支撑组的振动位移量最大值分别为17 mm、-20 mm，17 mm、-15 mm和17 mm、-20 mm。

3.4 接触刚度的指数型变化

设定第一支撑组与顶板接触刚度以指数曲线方式在0.1 s内由500 kN/m变为0，通过仿真得到这一过程中顶板、第一支撑组和第二支撑组的动态响应，如图6所示。

(a)接触刚度变化给定曲线

(b)顶板振动位移和振动加速度

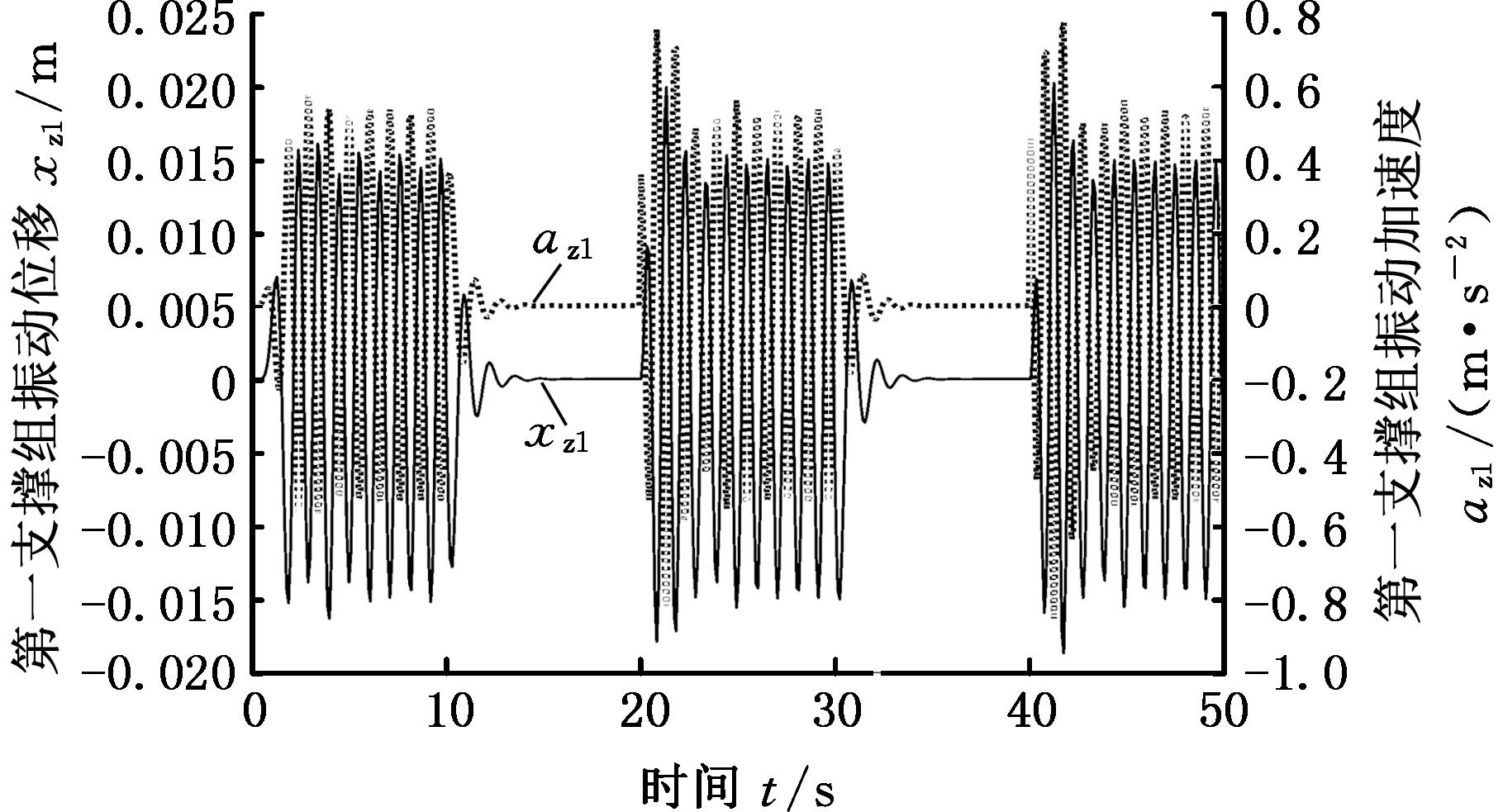
(c)第一支撑组振动位移和振动加速度

(d)第二支撑组振动位移和振动加速度图6 接触刚度指数变化的仿真结果Fig.6 Simulation results of contact stiffness logarithmic

仿真结果表明，第一支撑组下降时刻，顶板和第二支撑组的振动位移量最大值分别为16 mm、-15 mm和15 mm、-16 mm；第一支撑组上升时刻，顶板、第一支撑组和第二支撑组的振动位移量最大值分别为16 mm、-18 mm，16 mm、-12 mm和15 mm、-18 mm。

3.5 仿真结果分析

(1)迈步前后振动量达到稳定后，使用不同的迈步方法，顶板、第一支撑组和第二支撑组的振动量相差不大。

(2)使用阶跃突变方式进行支架迈步过程接触刚度控制时，会引起顶板和各个支撑组的剧烈振动。

(3)使用指数型变化方式进行支架迈步过程接触刚度控制时，能够有效降低迈步过程引起的顶板和各个支撑组的振动，顶板振动幅度约下降34.6%，第一支撑振动幅度约下降34.8%，第二支撑振动幅度约下降31.3%。

4 超前支架迈步过程动态响应实验

通过超前支架实验模型样机对超前支架迈步过程动态响应特性进行实验研究。使用液压缸实现顶板加载。超前支架样机及测试系统如图7a所示，使用江苏东华DH5922N动态信号测试分析系统、DH311E三向加速度传感器、DH5857电荷适调器、以及DELL precision 5110工作站进行实验研究。超前支架顶梁及振动传感器如图7b所示。

(a)超前支架样机 (b)超前支架顶梁与测试系统及振动传感器图7 超前支架样机Fig.7 Prototype model of advanced supporting

本文在实验中通过控制电液伺服阀阀芯位移实现超前支架与顶板接触刚度按照设定的曲线变化。超前支架第一支撑组和第二支撑组的质量均为2000 kg，超前支架刚度为500 kN/m。

测试超前支架在迈步过程中，使用不同的下降和上升支撑组的方式，顶板、第一支撑组、第二支撑组的变形量曲线如图8所示。

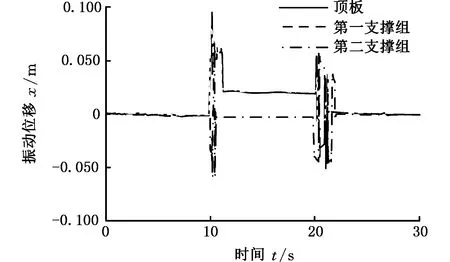
(a)接触刚度阶跃突变的测试结果

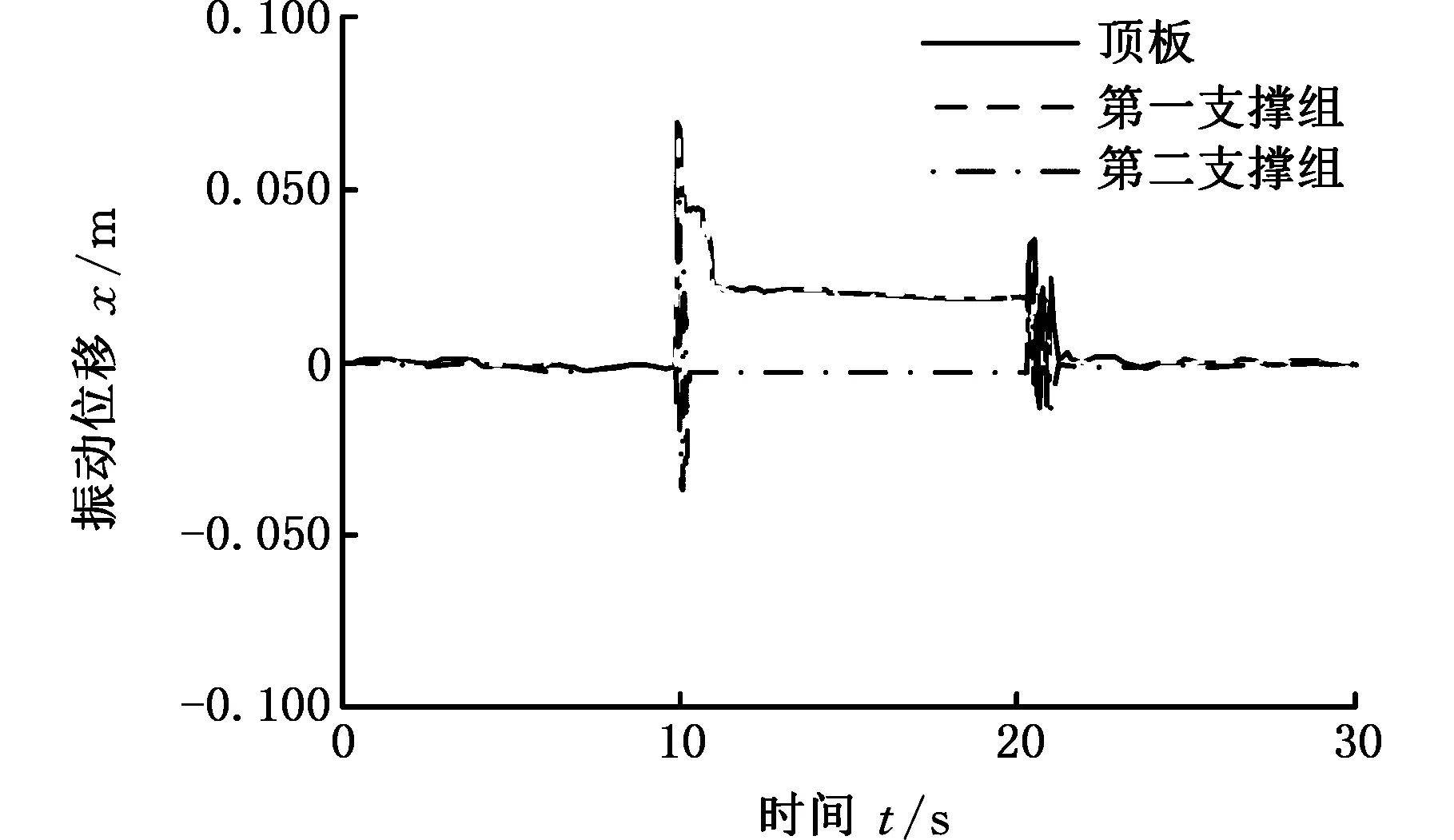
(b)接触刚度指数变化的测试结果

(c)接触刚度直线变化的测试结果

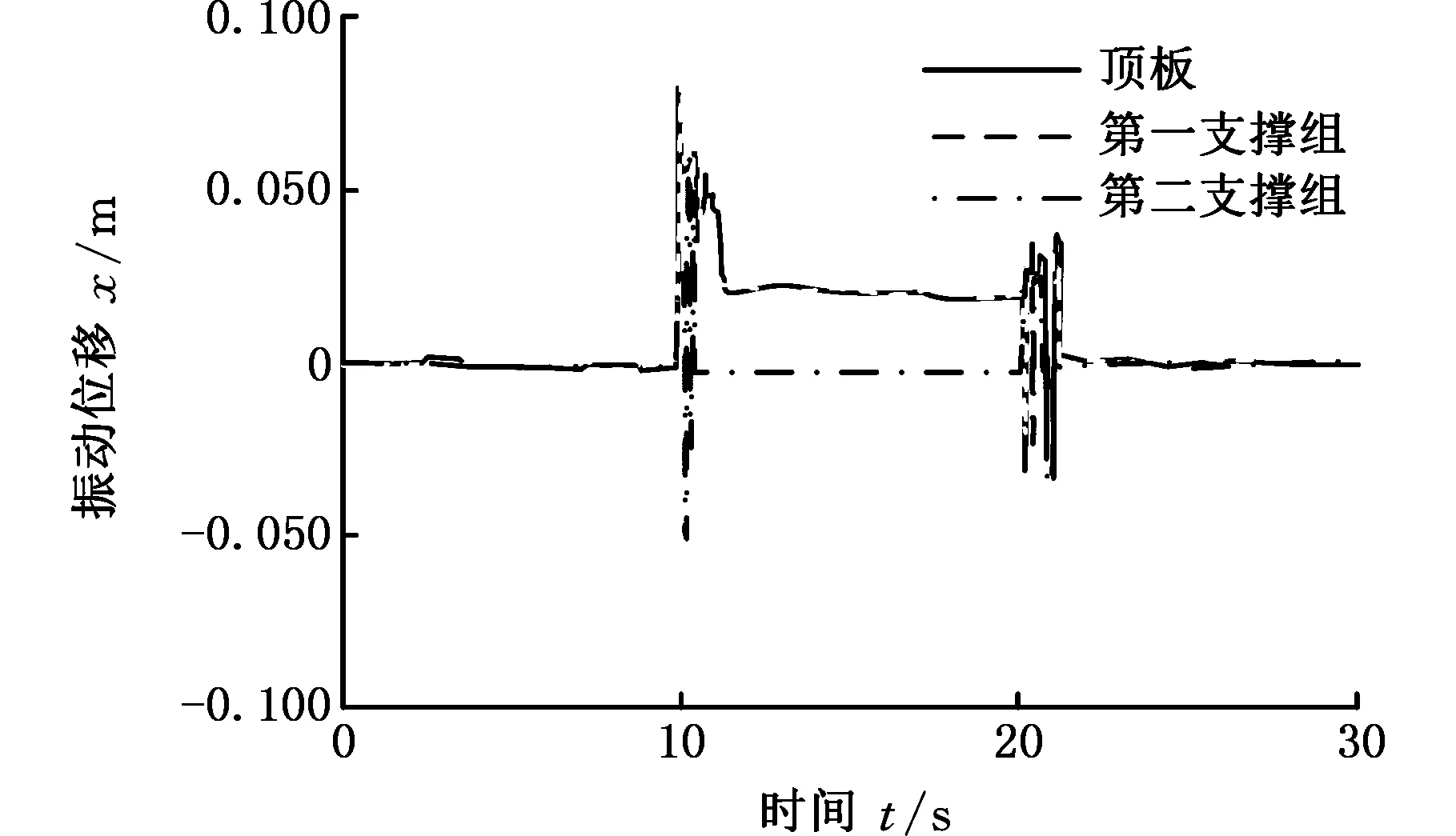
(d)接触刚度对数变化的测试结果图8 顶板、第一和第二支撑组的变形量测试曲线Fig.8 Deformation curves of top plate, first and second support groups

测试结果表明：使用阶跃突变方式进行支架迈步过程接触刚度控制时，会引起顶板和各个支撑组的剧烈振动；使用对数型、直线型和指数型刚度变化方式进行迈步过程控制时，能够减小顶板、第一支撑组和第二支撑组的振动量，并且三种方式减小振动量的效果逐渐递增。使用指数型变化方式进行支架迈步过程接触刚度控制时，相对阶跃突变方式，能够有效降低迈步过程引起的顶板和各个支撑组的振动，顶板振动幅度约下降29.8%，第一支撑振动幅度约下降28.7%，第二支撑振动幅度约下降26.9%。

5 结论

(1)本文通过数值仿真和实验方法对超前支架迈步过程的动态响应特性进行研究，结果表明：迈步前后振动量达到稳定后，使用不同的迈步方法，顶板、第一支撑组和第二支撑组的振动量相差不大。

(2)使用阶跃突变方式进行支架迈步过程接触刚度控制时，会引起顶板和各个支撑组的剧烈振动。

(3)使用对数型、直线型和指数型刚度变化方式进行迈步过程控制，能够减小顶板、第一支撑组和第二支撑组的振动量，并且三种方式减小振动量的效果逐渐递增。

[1] 卢进南,毛君,谢苗,等.巷道超前支架全支撑态动力学模型[J].煤炭学报,2015,40(1):50-57. LU Jinnan, MAO Jun, XIE Miao, et al. Dynamics Model of Advanced Powered Support in Heading under Full Support Situation[J].Journal of China Coal Society,2015,40(1):50-57.

[2] 谢苗,白雅静,毛君,等.不同工况下超前支护装备的模态分析[J].工程设计学报,2015,22(3):236-242. XIE Miao，BAI Yajing，MAO Jun，et al. Modal Analysis of Supporting in Advance Equipment under Different Working Conditions[J]. Chinese Journal of Engineering Design,2015,22(3):236-242.

[3] 栾丽君, 姚立泽, 齐建峰，等. 自移式掘进机辅助支护设备立柱力学分析[J].辽宁工程技术大学学报(自然科学版)，2013，32(4):527-530. LUAN Lijun, YAO Lize, QI Jianfeng, et al. Column Mechanics Analysis of Self-motion Assistanced Powered Support Equipment for Tunneling Machine[J]. Journal of Liaoning Technical University(Natural Science), 2013，32(4):527-530.

[4] 栾丽君, 任金萍, 卢景文.巷道用自移式辅助支护设备顶梁的优化及有限元分析[J].煤矿机械，2010，31(3):93-94. LUAN Lijun, REN Jinping, LU Jingwen. Optimization and Finite-element Analysis of Self-motion Assitanced Powered Support Equipment for Roadway[J]. Coal Mine Machinery, 2010,31(3):93-94.

[5] 谢苗,刘治翔,毛君,等.迈步式超前支护系统设计与支护特性研究[J].机械强度,2016,38(2):302-310. XIE Miao, LIU Zhixiang, MAO Jun, et al. Design on Step-type Advanced Supporting System and Research on the Support Characteristics [J].Journal of Mechanical Strength, 2016,38(2):302-310.

[6] 毛君,郑广辉,谢苗,等.基于Fuzzy-PID的超前支护装备支撑力自动控制系统[J].智能系统学报,2015,10(7):56-60. MAO Jun, ZHENG Guanghui, XIE Miao, et al.Support Force Automatic Control System of Advanced Supporting Equipment Based on Fuzzy-PID[J]. CAAI Transactions on Intelligent Systems,2015,10(7):56-60.

[7] 谢苗,刘治翔,鲁启通,等.超前支架迈步过程稳定控制方法研究[J].中国安全科学学报, 2015,25(3):54-59. XIE Miao, LIU Zhixiang, LU Qitong, et al. Study on Method for Controlling Stability of Advanced Support in Step Process[J].China Safety Science Journal,2015,25(3):54-59.

[8] 谢苗,刘治翔,池城,等.巷道超前支架的电液伺服位置压力复合控制方法[J].中国机械工程,2016, 27(2):239-245. XIE Miao, LIU Zhixiang, CHI Cheng, et al. Electro-hydraulic Servo Position and Pressure Hybrid Control Method of Forepoling System on Tunnelling[J]. China Mechanical Engineering,2016,27(2):239-245.

[9] 谢苗,刘治翔,毛君.综掘巷道超前支护装备多缸同步控制方法研究[J].工程设计学报,2015,22(2):193-200. XIE Miao, LIU Zhixiang, MAO Jun. Multi-cylinder Synchronous Control Method for Advanced Support of Roadway Support Equipment[J]. Chinese Journal of Engineering Design,2015,22(2):193-200.

[10] 唐治,潘一山,王凯兴.冲击地压巷道围岩支护作用动力学分析[J].岩土工程学报,2015,37(8):1532-1538. TANG Zhi, PAN Yishan, WANG Kaixing. Dynamic Analysis of Support for Surrounding Rock of Rockburst Roadway [J]. Chinese Journal of Geotechnical Engineering,2015,37(8):1532-1538.

[11] 潘一山,王凯兴,肖永惠.基于摆型波理论的防冲支护设计[J].岩石力学与工程学报,2013,32(8):1537-1543. PAN Yishan, WANG Kaixing, XIAO Yonghui. Design of Anti-scour Support Based on Theory of Pendulum-type Wave [J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(8):1537-1543.

(编辑 王旻玥)

Analysis of Influences of Contact Stiffness Variations on Advanced Support Dynamic Response in Moving Processes

XIE Miao LIU Zhixiang MAO Jun
School of Mechanical Engineering,Liaoning Technical University,Fuxin，Liaoning,123000

The dynamic response characteristics of advanced support during the stepping processes were studied by numerical simulation and experiments. A coupling dynamic model of advanced support and roof was established with block rock theory. The stepping processes of advanced support were simulated with the contact stiffness changes between support and roof. The dynamic responses of the roof, the first and the second support groups were researched by changing the steps of advanced support and top contact stiffnesses, in the form of step mutation, exponential, linear and logarithmic. MATLAB was used to establish dynamic differential equation of advanced supports, and four order Runge-Kutta method was used to solve dynamics problems of advanced supports. The results of simulations and experiments show that abrupt vibrations of the roof and the support group may be caused by using the method of step mutation. The logarithmic, linear and exponential rigidity changing way were used to control stepping processes, that may reduce vibrations of the roof, the first and second support groups, and the effects of the three ways gradually increase.

advanced support; contact stiffness; dynamic response; moving process

2016-06-21

国家自然科学基金资助项目(51304107)；辽宁省教育厅创新团队项目(LT2013009)；辽宁省教育厅重点实验室项目(LJZS006)。

TD353

10.3969/j.issn.1004-132X.2017.12.004

谢 苗，女，1980年生。辽宁工程大学机械工程学院副教授、博士研究生导师。主要研究方向为机械动态设计及仿真、机电一体化。E-mail：xiemiao1121@126.com。刘治翔，男，1988年生。辽宁工程大学机械工程学院博士研究生。毛 君，男，1960年生。辽宁工程大学机械工程学院教授、博士研究生导师。