大行程精密定位平台偏摆误差的补偿方法
刘吉柱, 李 健, 张雯雯, 王阳俊, 潘明强, 陈立国
(1.苏州大学机电工程学院 苏州,215021) (2.苏州大学苏州纳米科技协同创新中心 苏州,215021)
大行程精密定位平台偏摆误差的补偿方法
刘吉柱1,2, 李 健1,2, 张雯雯1,2, 王阳俊1,2, 潘明强1,2, 陈立国1,2
(1.苏州大学机电工程学院 苏州,215021) (2.苏州大学苏州纳米科技协同创新中心 苏州,215021)
精密定位平台在导轨动连接处刚度较差,在高速高动态工作中这里易产生偏摆振动。为了减小偏摆误差对定位平台的影响,提高定位精度,通过对直线电机驱动、气浮导轨支撑和导向的高精度定位平台进行研究。根据定位平台偏摆误差的动态特性,采用偏摆误差补偿方法,设计一种偏摆误差检测系统,采用平尺和微位移传感器相结,具有高频响、非接触式的特点。设计了一种基于压电陶瓷驱动的x,y两维微位移补偿机构。同时,通过将气浮导轨滑块副简化成弹簧、质量和阻尼相结合的系统,推导出了定位平台两自由度的偏摆振动模型。基于误差补偿系统的偏摆误差补偿实验表明,精密定位平台的定位精度得到了较大提高,定位平台的定位精度优于2 μm。
偏摆误差; 振动模型; 压电陶瓷; 误差补偿
引 言
随着纳米光刻、微机电系统(micro-electro-mechanical system,简称MEMS)封装、超精密加工、微电子工程及生物医学工程等领域的迅速发展,对定位平台的动静态特性要求也越来越高,定位系统的发展也将促进超精密加工、精密测量及大规模集成电路等行业的发展。在大规模集成电路制作中,电路板上的布线密度越来越高,线路的修复、连接质量等都对加工行程、速度与精度提出了较高的要求[1]。芯片封装作业中,芯片的安装、固定、密封和引线键都需要高精度的定位平台装置来完成[2]。光刻技术方面,如对光学镜头进行表面轮廓的测量与误差补偿、粗糙表面的微纳米加工、镀膜、移动平台的行程及定位精度等都提出了极高的要求[3-4]。随着高精密领域的不断发展,定位平台呈现出大行程、高精度的发展趋势[5-6]。然而大行程与高精度相互矛盾统一,当定位平台行程越大,机构的设计及外界环境对定位平台的定位精度影响越大。目前,通过对定位平台进行误差补偿从而提高定位精度的方法,许多国内外学者已经做了大量研究,并取得了一系列的成果[7-9]。
对于纳米压印平台,偏摆误差是影响其定位精度的关键因素[10]。笔者针对平台的偏摆误差进行建模分析,建立了偏摆误差检测模型,研究了基于偏摆误差补偿的定位系统,改善了定位平台精度。
1 偏摆误差分析及模型的建立
纳米压印平台采用XY-table型串联结构,如图1所示。其上、下直线运动轴采用超精密静压气浮导轨支承和导向,无铁芯直线电机驱动,采用精密光栅尺进行位移反馈,从而实现了无磨损的直接驱动,并结合了气体静压导轨和直线电机的优点,目前也是高精密领域定位平台的典型代表。定位平台进行直线运动时,不可避免地会产生几何误差以及平台的偏摆振动误差,然而定位平台的偏摆振动误差作为动态误差,特性复杂,大小、方向都随时改变[11]。
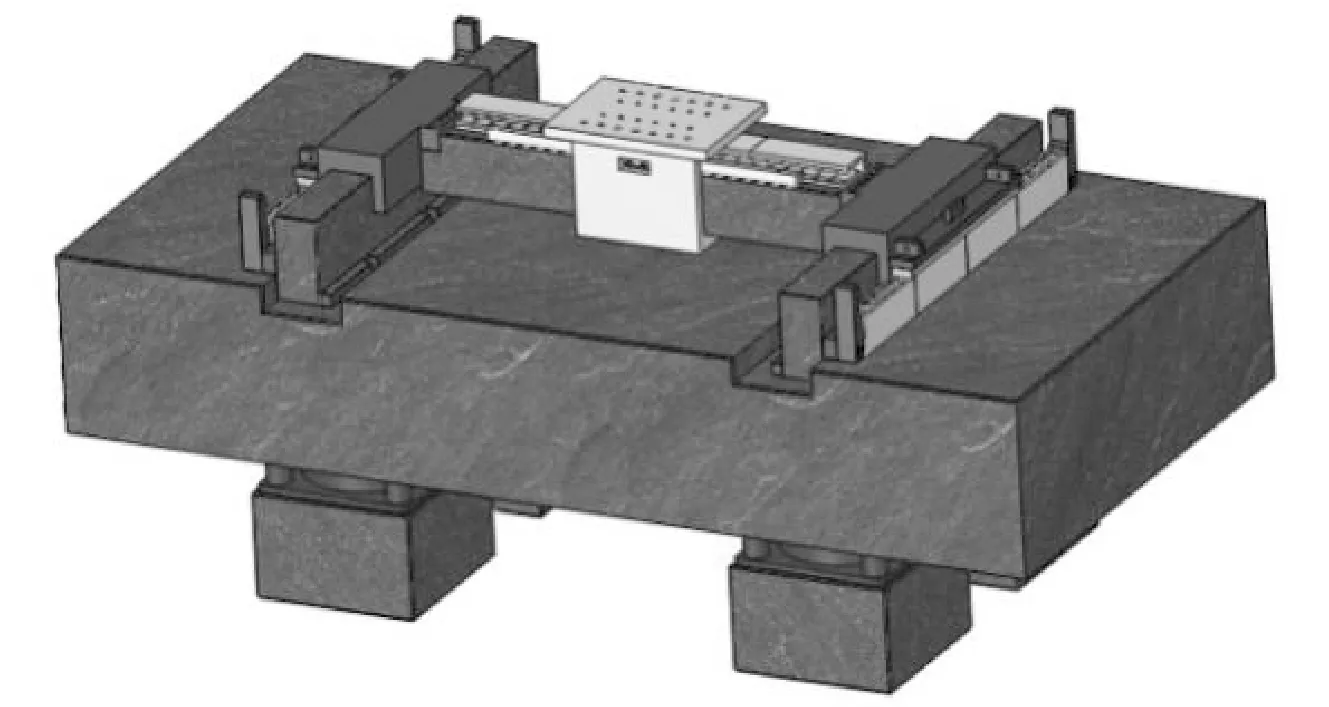
图1 大行程纳米压印平台Fig.1 Large stroke nano imprint platform
1.1 几何误差分析及模型建立
由于高精度定位平台x轴和y轴采用串联方式,所以可分别计算两轴几何误差,通过对两轴误差进行叠加,可得高精度定位系统末端的综合误差。在平台侧面安装4路位移传感器A,B,C和D,分别建立x,y轴定位平台的几何误差模型,如图2、图3所示。

图2 x轴平台几何误差模型Fig.2 x-axis platform geometric error model
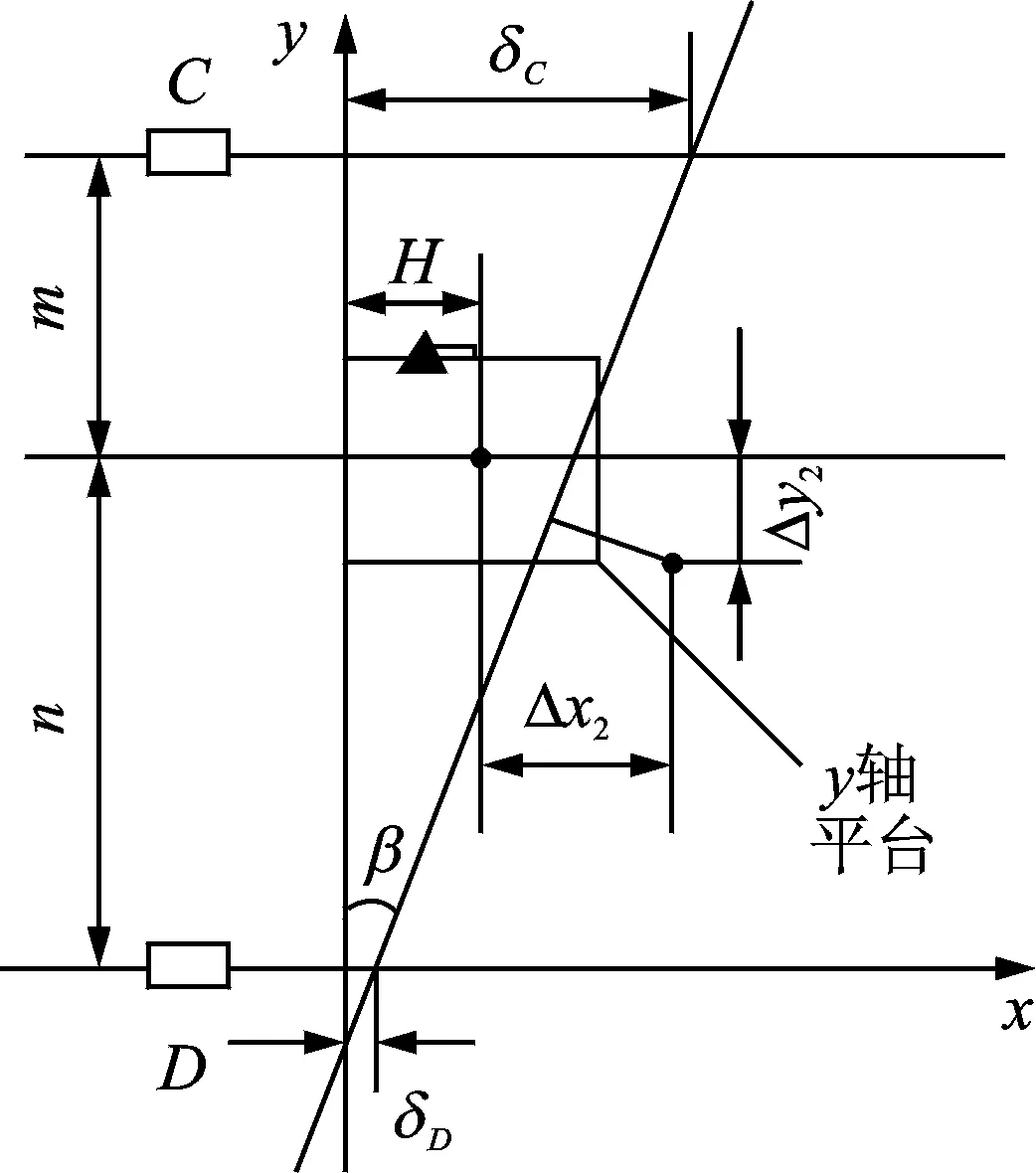
图3 y轴平台几何误差模型Fig.3 y-axis platform geometric error model
通过将定位平台x轴和y轴偏摆误差进行叠加,定位平台的综合几何误差公式推导如下
(1)
由式(1)可知,精密定位系统的几何误差可通过4路传感器的位移变化δA,δB,δC和δD进行描述。
1.2 偏摆振动模型建立
为进一步简化分析,可将导轨滑块副简化成由弹簧-质量-阻尼相结合的系统,并假设平台两轴方向的直线电机作用力和等效刚度都作用在各轴平台质心处,最终建立定位平台的偏摆振动模型,如图4所示。由于导轨固定在平台基座上,且每根导轨上有2个滑块,因此可使两侧对称的导轨滑块副的刚度和阻尼系数分别简化为刚度K1,K2,K3,K4和C1,C2,C3,C4。同理,Kox,Koy和Cox,Coy分别为平台在x轴和y轴方向简化之后的直线电机驱动刚度和等效阻尼系数。
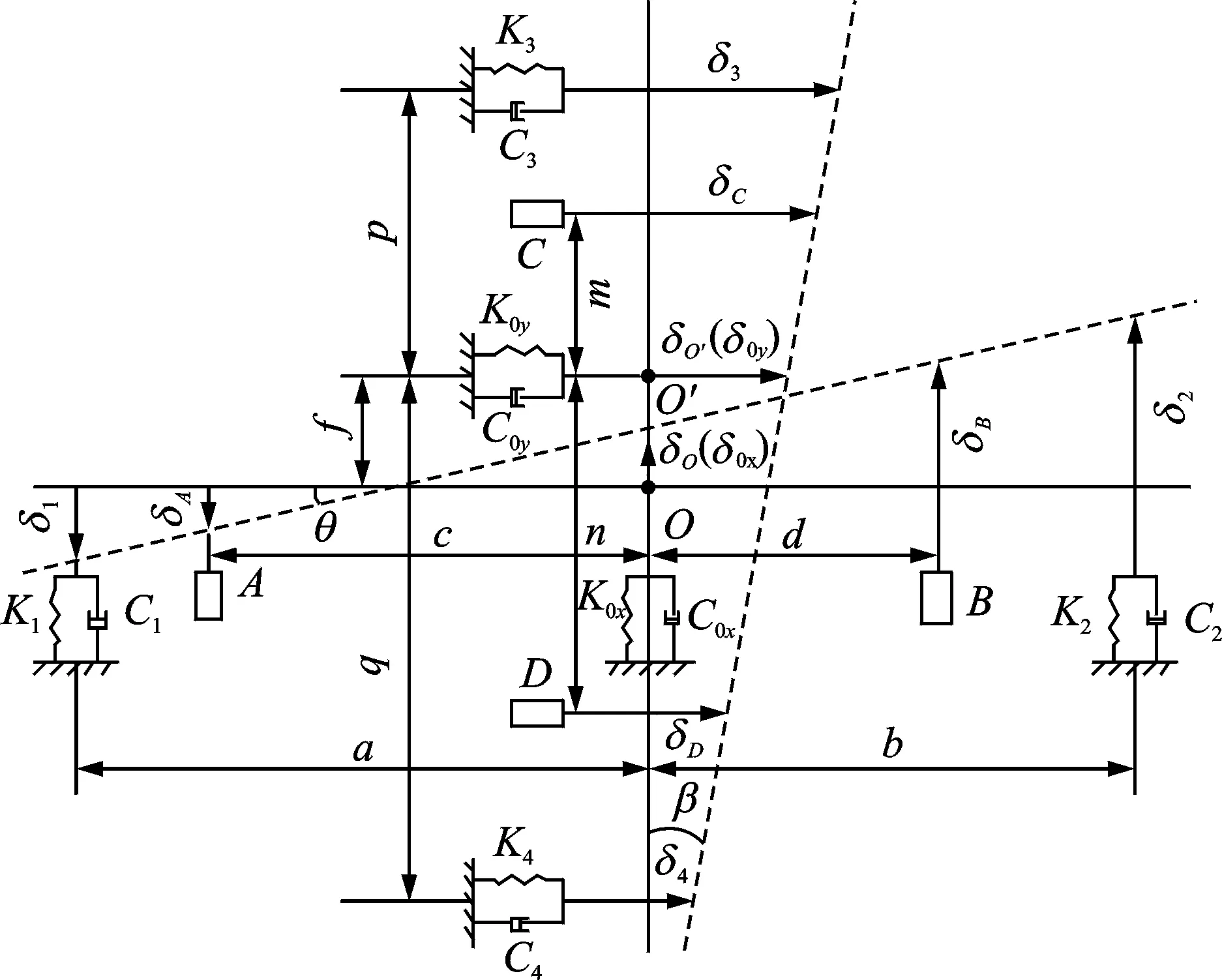
图4 定位平台偏摆振动简化模型Fig.4 Simplified yaw vibration model of positioning platform
根据图4,对x轴定位平台刚体应用质心运动定律和刚体转动定律,建立其运动微分方程
(2)
其中:Mx为x,y轴平台的共同质量;Jx为x,y轴平台绕其质心的转动惯量。
将K1=K2=2K,K0x=2K0,C1=C2=2C,C0x=2C0带入式(2)得
(3)
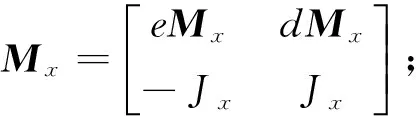
Cx=
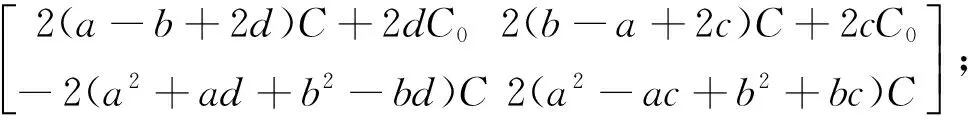
式(3)的解为
(4)
其中:Aij由施加于定位平台的初始条件决定。
同理,对y轴定位平台刚体应用质心运动定律和刚体转动定律,建立运动微分方程,得运动微分方程的解为
(5)
将精密定位平台x,y轴的运动微分方程的解进行叠加,得到平台的综合偏摆振动方程
(6)
根据以上分析,可以得到定位平台的偏摆振动固有频率和系统末端工作点的偏摆运动轨迹,为偏摆误差检测和误差补偿提供理论参考。
2 偏摆误差检测方法
针对所研究的定位平台偏摆误差特点,设计一种偏摆误差检测系统。采用平尺和电容式微位移传感器相结合的方式,将非接触式平尺连接支架固定在定位平台上,微位移传感器固定在工作台侧面的基座上,该系统具有动态性能好和分辨率高等优点。
在平台运动过程中,通过检测位移传感器与平尺间相对位移的变化,根据检测算法得出平台的偏摆误差。
分别以传感器A,D为坐标原点建立直角坐标系,得到x,y轴定位平台的偏摆误差检测模型,如图5,6所示。当x,y轴分别产生进给位移Sx和Sy时,可得x轴方向定位系统末端点的偏摆误差为
(7)
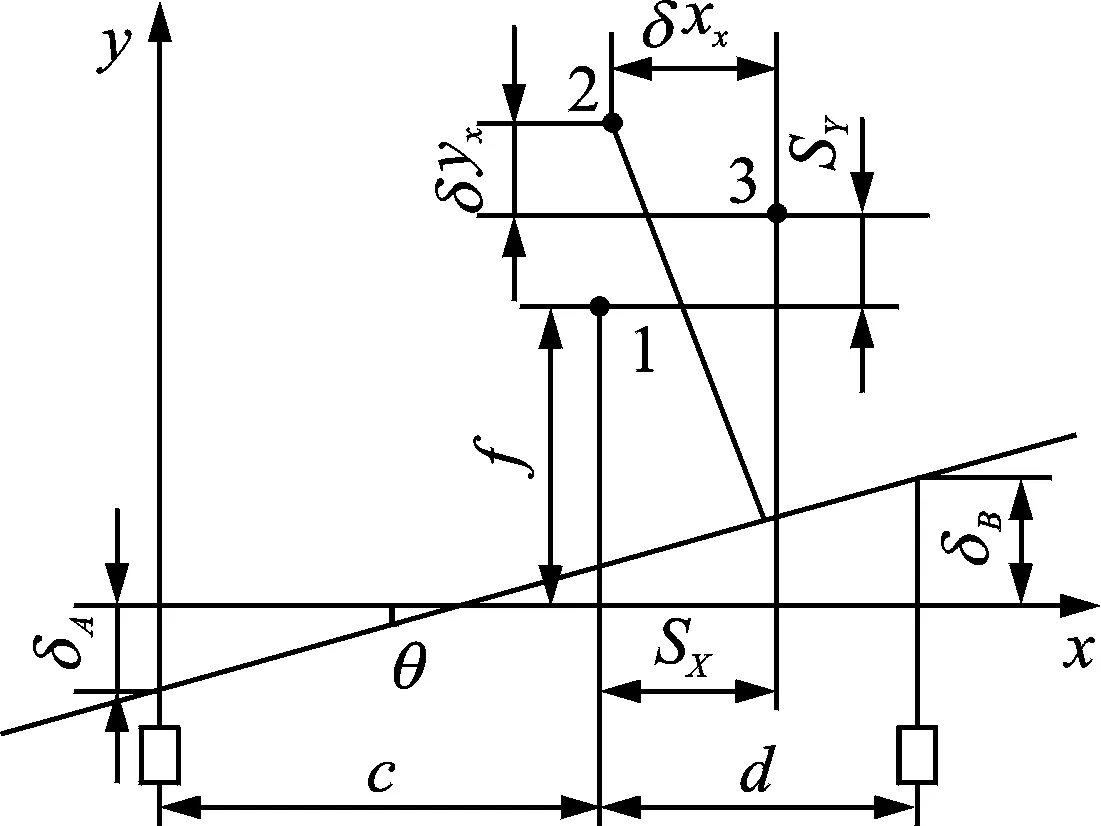
图5 x轴定位平台偏摆误差检测模型Fig.5 x-axis positioning platform yaw error detection model
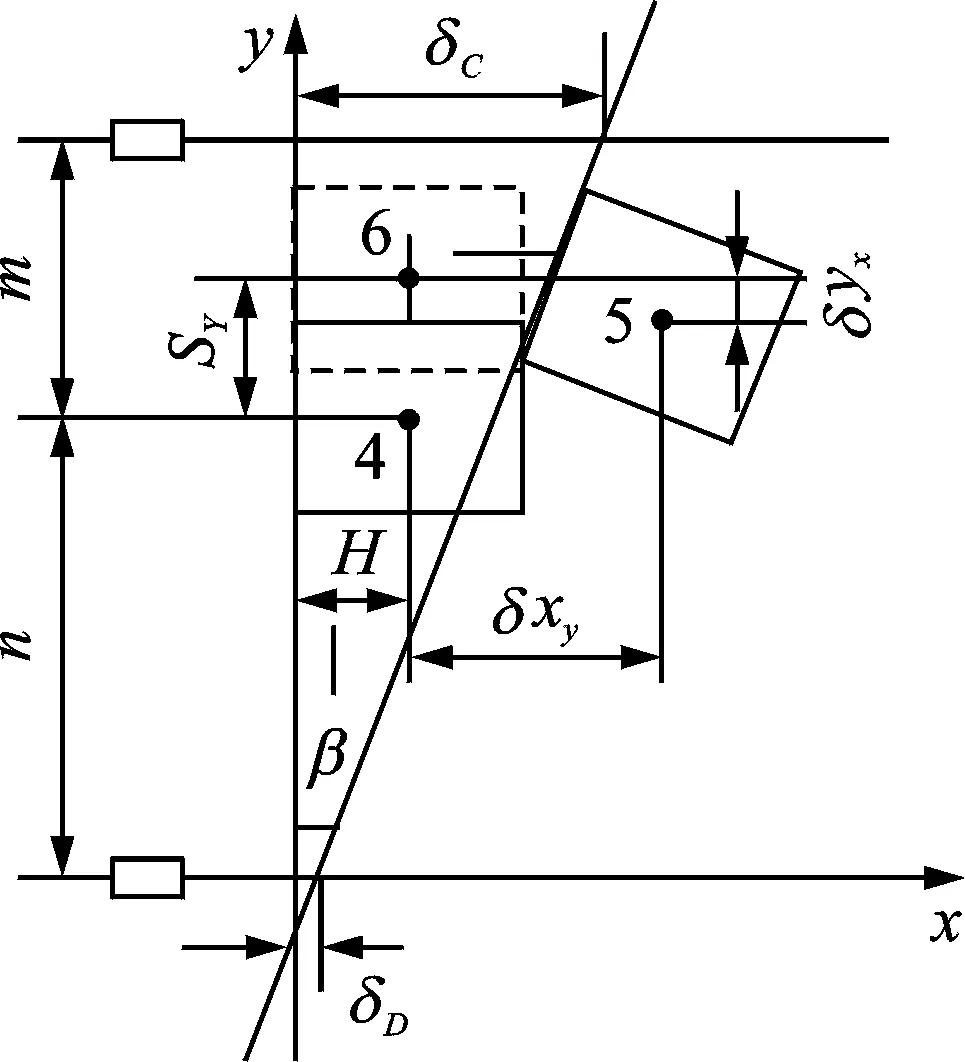
图6 y轴定位平台偏摆误差检测模型Fig.6 y-axis positioning platform yaw error detection model
同理可得y轴方向定位系统末端点的偏摆误差
(8)
通过将x和y轴的偏摆误差进行叠加,推导可得定位系统末端的综合偏摆误差如下
(9)
根据式(9)可知,定位系统末端点的综合偏摆误差值与以下参数有关:精密定位平台的初始位置、电容传感器的安装位置、定位平台的运动距离和位移传感器检测的位移变化量。
3 偏摆误差补偿机构
笔者通过设计二维微动误差补偿平台对定位平台进行偏摆误差补偿。补偿效果是否理想关键在于微动误差补偿平台的设计是否合理有效,其对缩短误差补偿系统的稳定时间和提高系统的补偿效果具有重要作用;因此,所设计的微动误差补偿平台需要具有一定的补偿范围、较高的动态特性和位移分辨率。笔者提出以下性能指标:
1) 重量轻、响应快,能实现高速、高加速度运动;
2) 工作行程达到10 μm以上,满足误差补偿范围要求;
3) 位移耦合度低于2%,满足定位系统定位精度的要求;
4) 固有频率大于1 kHz,满足定位平台偏摆误差实时补偿要求。
笔者采用压电陶瓷驱动,结合椭圆形机构、直角平板柔性铰链和平板柔性铰链设计了一种单平面二维微动补偿平台,不仅具有体积小、重量轻和结构简单等优点,而且其位移耦合度小,动态特性好,能够进行大行程定位平台的偏摆误差实时补偿。
3.1 微动误差补偿平台的设计
微动误差补偿平台机构如图7所示,工作台的四角采用4个对称的直角平板柔性铰链,此结构不仅能够有效减小机构中存在的交叉耦合位移,而且在一定程度上能减小外界的干扰。在工作台与椭圆形机构之间采用平板柔性铰链进行连接,通过控制其尺寸使微动平台在x,y方向的位移耦合最小,更好地达到误差补偿、提高定位精度的要求。压电陶瓷选用PTBS150/7×7/20型驱动器,其具有刚度大、推力大及响应快等优点。压电陶瓷驱动电源为HPV-150型驱动电源,采购于哈尔滨工业大学博实精密测控有限公司。
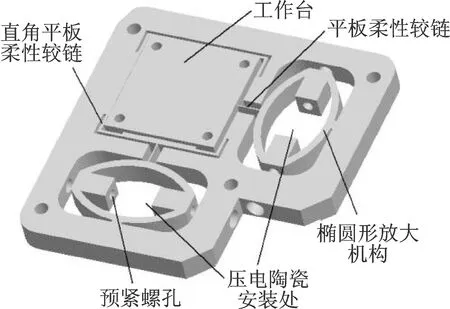
图7 微动误差补偿平台机构图Fig.7 Organization chart of the micro-positioning stage
设计要求微定位平台输出位移约为10 μm,压电陶瓷的输出位移设计为14 μm,根据椭圆形机构刚度公式可得
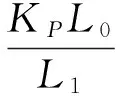
(10)
其中:L1为PZT实际输出位移;L0为PZT无外载时的名义输出;Kp为PZT刚度;K为椭圆形机构的刚度。
由于椭圆形机构是全对称结构,可将其简化为如图8所示机构。其中:p为压电陶瓷作用在椭圆形机构的作用力;″L为力p引起的实际输入位移。由于直角平板柔性铰链的刚度Kc作用产生力F,从而将抑制A点的位移x。
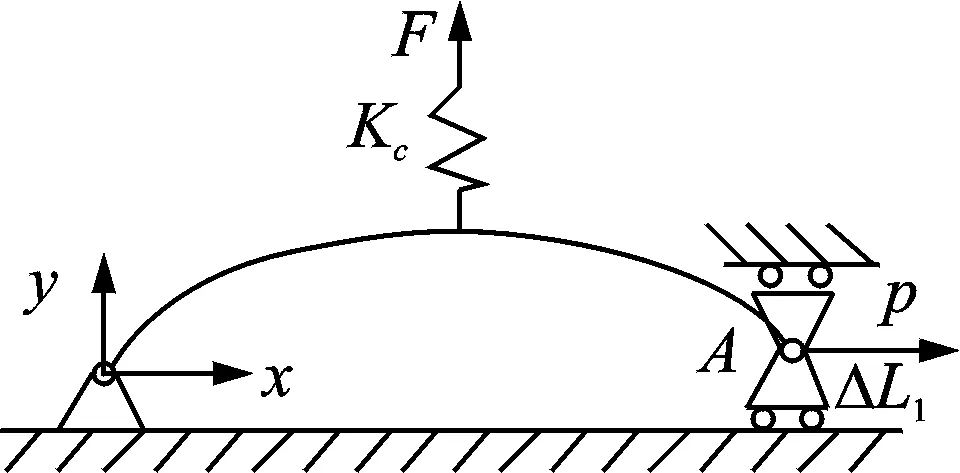
图8 椭圆形机构简化图Fig.8 Simple diagram of the oval amplification mechanism
工作台四角的直角平板柔性铰链完全对称,忽略x,y方向的耦合作用,将其简化为基本静定系进行分析,可推导出直角平板柔性铰链在x,y方向的刚度为
Kx=Ky=Kc=5Ebt3/2L3
(11)
根据式(5)及以上分析可知,不仅椭圆形机构的参数会影响其刚度,直角平板柔性铰链几何参数宽度b和厚长比e(e=t/L)的增加将使工作台部分刚度增大,从而抑制A点的位移''L,使椭圆形机构在如图8所示的x方向刚度K增大。
3.2 微动误差补偿平台的有限元分析
微定位平台材料选用Al7075,其重要参数如下:弹性模量为72 GPa,泊松比为0.31,屈服极限为505 MPa,密度为2 800 kg/m3。ANSYS分析时采用3维20节点实体单元(SOLID95)进行智能划分。
通过对微定位平台进行模态分析,可以仿真得到其固有频率和对应振型,以了解定位系统动态特性,对微动补偿平台的设计具有重要作用。图9为对选定参数的微定位平台进行模态分析得到的第1阶振型图。可以看出,微定位平台的第1阶固有频率为1 068 Hz。因此,微定位平台动态特性较好,能有效避免环境振动对工作台的影响,满足设计要求。
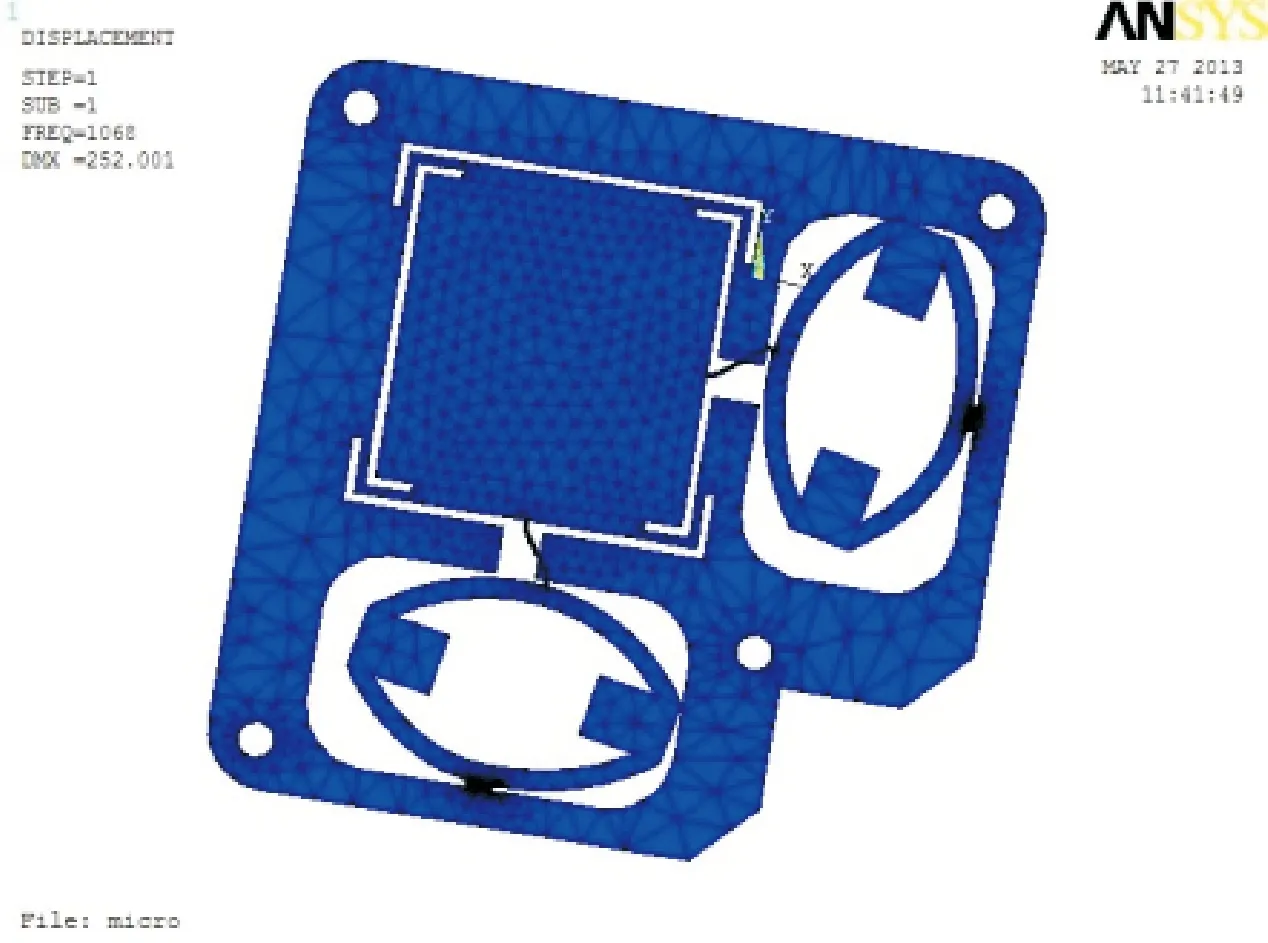
图9 微动台第1阶阵型Fig.9 The first vibration mode of the stage
对选定参数的微定位平台的3D模型进行有限元仿真,确定其刚度及应力是否达到要求。在x,y方向的压电陶瓷均加载300 N的力时,可得椭圆形机构与压电陶瓷接触处产生的位移约等于设计位移14 μm(略大于此处的设计位移10.5 μm)。其应力结果对检验微定位平台的强度有效微动台的应力分布云图见图10,最大应力发生在平板铰链连接处,大小为46.915 MPa<[σ]=50.5 MPa,满足要求。
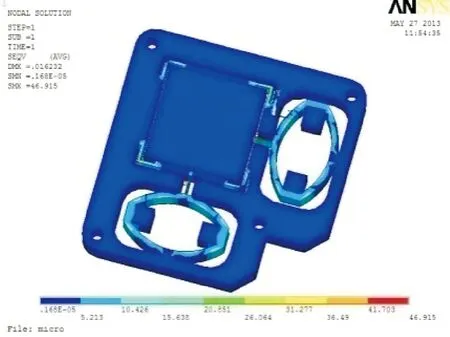
图10 加载300 N时微动台的应力分布云图Fig.10 Stress contour of the stage loaded 300 N
椭圆形机构在单方向加载300N的力时,输出位移L1为14.911 μm。工作台末端中点在x方向产生进给位移x约为10.900μm。由于平板铰链的影响,工作台末端中点在y方向产生的耦合位移Δy约为0.118 μm。因此,微定位平台的位移耦合度为1.083%,位移耦合较小,微定位平台的位移输出系数ξ=0.731。椭圆形机构的刚度K和工作台的最大进给位移ΔS分别为
通过仿真结果可知,所设计的二维微动补偿平台刚度和行程均能满足设计要求。
4 偏摆误差补偿实验
大行程精密定位平台控制系统主要由大行程精密定位系统、偏摆误差检测系统和偏摆误差补偿系统组成。
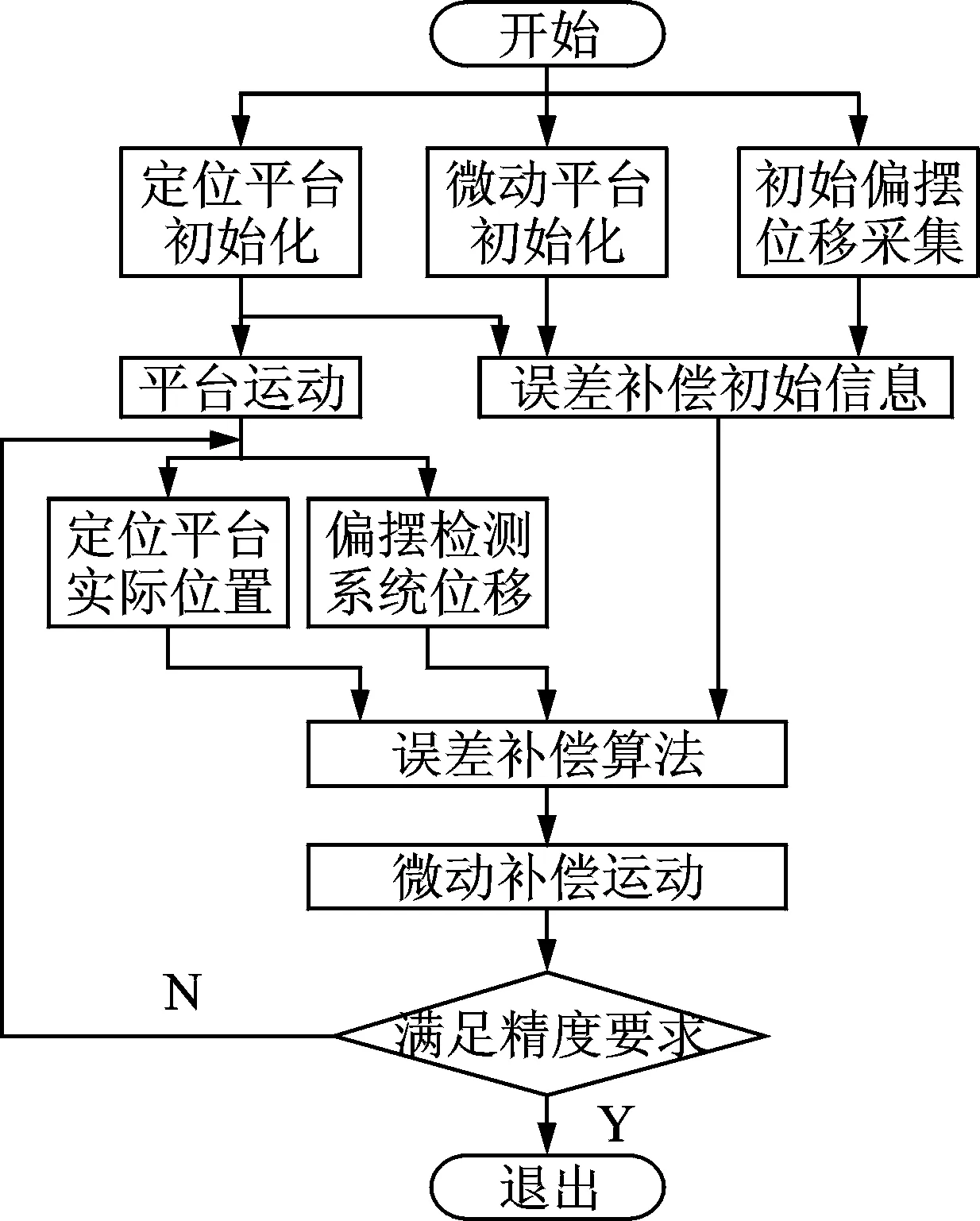
图11 偏摆误差补偿控制流程图Fig.11 The control flow graph of yaw error compensation
笔者搭建的偏摆误差检测系统,主要由上位机、数据采集卡、微位移传感器及固定安装的直线平尺等组成,通过位移检测传感器与平尺的相对距离变化,根据检测算法计算出偏摆误差的大小。微动误差补偿系统由控制计算机、微动误差补偿平台、数据采集卡、压电陶瓷及其驱动电源等组成。基于压电陶瓷驱动的微动误差补偿平台,采用椭圆形放大机构增加平台位移,由直角平板柔性铰链进行传动。偏摆误差补偿流程如图11所示,微动误差补偿系统根据偏摆误差检测系统检测结果对定位平台产生的偏摆误差进行误差补偿,从而提高其定位精度。
为检验偏摆误差补偿效果,使平台以最大速度分别在x,y轴平台的行程范围内按规划轨迹进行运动。图12为x轴偏摆误差测试曲线,其中:图(a)为未进行偏摆误差补偿时系统末端点的偏摆误差曲线,误差幅值约为3.5 μm;图(b)为误差补偿后系统末端点的偏摆误差曲线,误差幅值减小到0.9 μm,补偿效果明显。
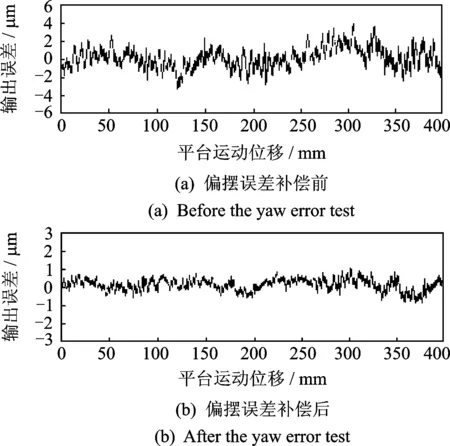
图12 x轴偏摆误差前后测试曲线Fig.12 x-axis yaw error curve before and after the test
采用相同方法,可得平台y轴偏摆误差测试曲线,如图13所示。其中:图(a)为未进行偏摆误差补偿时系统末端点的偏摆曲线,误差幅值约为3 μm;图(b)为进行误差补偿后系统末端点的偏摆误差幅值约为0.9 μm,补偿效果明显。
根据实验结果可知,所设计的微动补偿平台可以对大行程精密定位平台进行偏摆误差补偿,有效地改善了定位平台的定位精度,实现了大行程定位平台的精密定位。
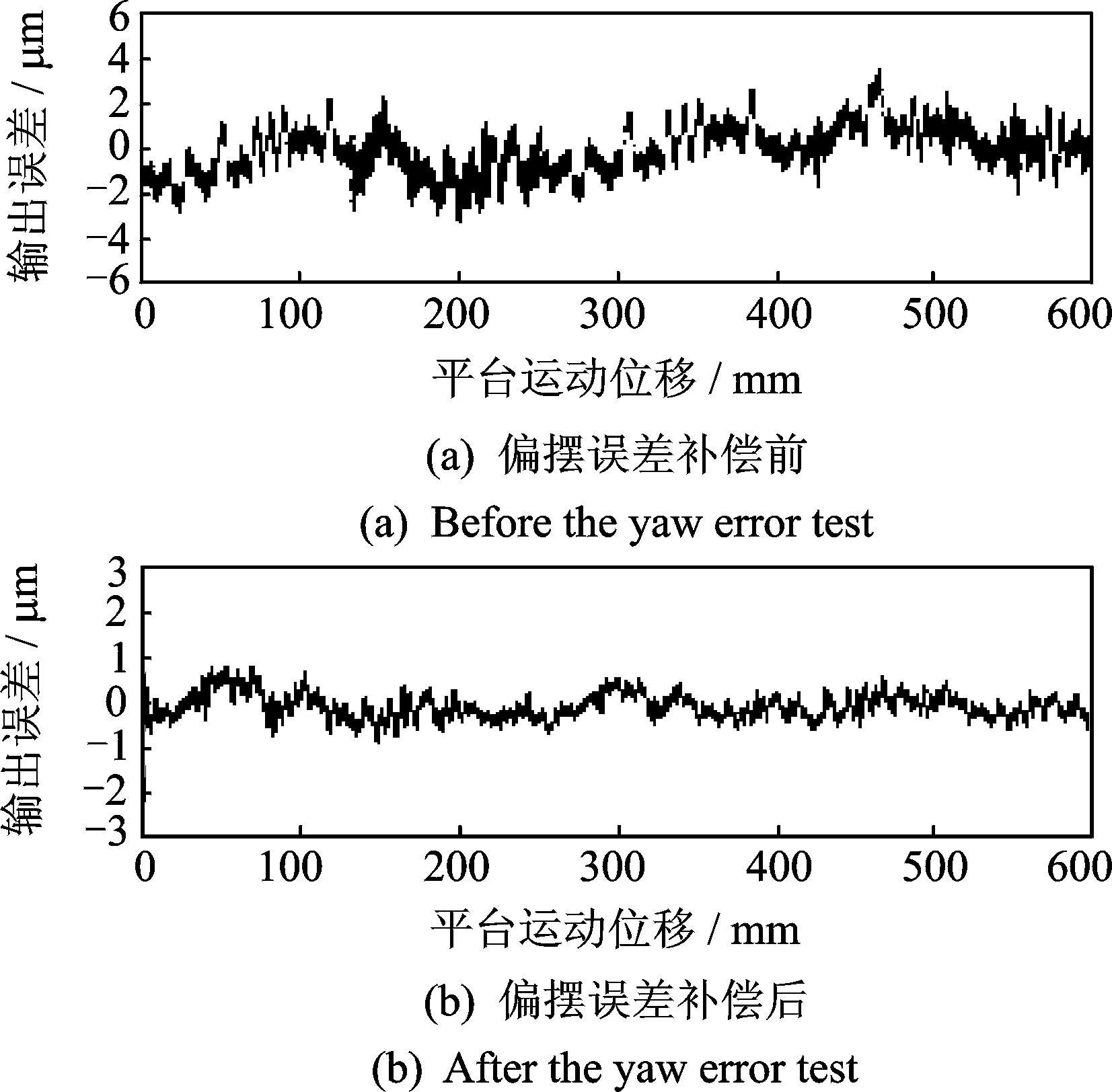
图13 y轴偏摆误差前后测试曲线Fig.13 y-axis yaw error curve before and after the test
5 结束语
通过分析大行程精密定位平台定位精度的偏摆误差,建立了相应的几何误差模型和偏摆振动模型,基于平尺和电容式位移传感器设计了非接触式的偏摆误差检测系统,得到偏摆误差检测算法。通过实验研究,采用压电陶瓷驱动、柔性铰链传动的微动补偿平台建立的误差补偿系统能够有效地对偏摆误差进行实时补偿,使大行程精密定位平台的定位精度优于2μm,验证了所研究误差补偿方法的正确性和可行性。
[1] Gu Yangqin, Chen Liguo, Liu Jizhu, et al. Design of a single-plane two-dimensional micro-positioning stage based on the oval amplification mechanism[C]∥IEEE International Conference on Information and Automation. Yinchuan,China:IEEE, 2013:1147-1152.
[2] Sun Lining, Jie Degang, Liu Yanjie, et al. Investigation on a novel dual-grating macro-micro driven high speed precision positioning system for NEMS[C]∥Proceedings of the IEEE/NEMS 2006 International Conference on Nano-Micro Egineered and Molecular Systems. Zhuhai, China: Insitute of Electrical & Electronics.Computer Society, 2006: 646-650.
[3] Yoshikazu Y, Akimasa S, Motoyuki S. Lithgraphy: its path of evolution and future trends[J]. Imaging Science and Photochemistry, 2012(1):1-8.
[4] 朱煜,尹文生,段广洪.光刻机超精密工作的研究[J].电子工业专用设备,2004(2):25-28.
Zhu Yi, Yin Wensheng, Duan Guanghong. Study on ultra precision of the photoetching machine[J]. For Special Equipment for Electronic Industry, 2004(2):25-28.(in Chinese)
[5] 林海波,杨国哲,黄小良.大行程超精密工作台的研究[J].机械设计与制造,2010, 6(6): 130-131.
Lin Haibo, Yang Guozhe, Huang Xiaoliang. Design of a large travel ultra precision stage[J]. Machinery Design & Manufacture, 2010, 6(6): 130-131. (in Chinese)
[6] Kwon S J, Chung W K. Robust and time-optimal control strategy for coarse/fine dual-stage manipulators[C]∥Proceedings of the 2000 IEEE International Conference on Robotics and Automation. San Francisco, CA: IEEE, 2000: 4051-4056.
[7] 刘建春,郭隐彪,邵明亮. 光学非球面检测平台误差补偿[J]. 振动、测试与诊断, 2011, 31(2):229-232.
Liu Jianchun, Guo Yinbiao, Shao Minliang. Error compensation for optical aspheric surface metrical platform[J]. Journal of Vibration,Measurement & Diagnosis, 2011, 31(2):229-232. (in Chinese)
[8] 刘明,章青. 运用多体理论和神经网络的机床热误差补偿[J]. 振动、测试与诊断,2010,30(6): 657-661.
Liu Min, Zhang Qin. Thermal error model and compensation of machining tool using multibody system theory and neural network[J]. Journal of Vibration, Measurement & Diagnosis,2010,30(6): 657-661. (in Chinese)
[9] 孙麟治,李鸣鸣,程维明.精密定位技术研究[J]. 光学精密工程,2005, 13(S): 69-75.
Sun Linzhi, Li Minmin, Chen Weimin. Study on precision positioning technique[J]. Optics and Precision Engineering, 2005, 13(S):69-75. (in Chinese)
[10]晏祖根,孙立宁. 高速精密定位平台的偏摆误差实时补偿[J]. 哈尔滨工业大学学报, 2009, 41(12): 290-294.Yan Zugen, Sun Lining. A novel precision positioning table based on real-time yaw error compensation[J]. Journal of Harbin Institute of Technology, 2009, 41(12): 290-294. (in Chinese)
[11]张春巍,李芦钰,喻言,等. 悬吊结构体系摆振响应测试及非线性误差修正[J]. 振动、测试与诊断,2010,30(3):227-231.
Zhang Chunwei, Li Luyu, Yu Yan, et al. Swing response measuring and nonlinear error modification of suspended structure system in pendulum vibration mode[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(3): 227-231. (in Chinese)
10.16450/j.cnki.issn.1004-6801.2017.03.013
国家自然科学基金资助项目(61273340);国家高技术研究发展计划(“八六三”计划)资助项目(2013AA041109)
2015-04-16;
2015-06-03
TH113.2; TH162; TG806
刘吉柱,男,1978年8月生,博士、副教授。主要研究方向为机电一体化技术、电机及驱动控制技术。曾发表《Selecting of the temperature measurement points for positioning platform with large trip and high precision thermally induced error compensation model》(《Applied Mechanics and Materials》Vol.431)等论文。 E-mail:liu_jizhu@163.com

