超声导波在圆管结构损伤定位中的应用

王国锋, 李富才, 刘志强， 孟 光

(上海交通大学机械系统与振动国家重点实验室 上海，200240)



超声导波在圆管结构损伤定位中的应用

王国锋, 李富才, 刘志强， 孟 光

(上海交通大学机械系统与振动国家重点实验室 上海，200240)

针对结构损伤会影响超声导波传播，提出基于超声导波无损检测的结构健康监测方法。以内径为174 mm、外径为194 mm、材料为20#碳钢的圆管结构为例，根据频散方程利用数值法求解其纵向模态以及周向Lamb波频散曲线。同时考虑其频散曲线和波的结构，确定激励频率中心频率为80 kHz。在此基础上进行有限元仿真，验证圆管中导波的传播机理及特征。针对此频率圆管纵向模态导波以及周向Lamb波的频散特性、波的结构比较接近，且都与板中的Lamb波相似，从而提出了单点激励、多点接收，并采用椭圆定位的方法，实现圆管结构损伤定位。通过仿真和实验验证该方法对切槽、圆孔等损伤的识别效果，并对损伤定位误差的影响因素进行了分析。

导波； 圆管； 频散； 损伤定位； 结构健康监测

引 言

管道结构及其相关设备在服役过程中，由于受到冲击载荷、材料老化、腐蚀和外界环境变化的影响，导致结构表面或者内部存在损伤，造成结构承载能力减弱，严重时甚至造成巨大的灾难。因此，结构健康监测就尤为重要，通过结构健康监测，可以提前做出判断，减少灾难性事故的发生。同传统无损检测技术相比，基于超声导波的方法可实现大范围检测，受人为因素影响相对较小，并且能够实现实时在线检测。近年来基于超声导波的无损检测技术，在结构健康监测方面取得很大的发展，成为结构健康监测领域重要的研究方向之一[1-5]。

在管道结构导波理论以及应用方面，国内外学者做了很多研究。Gazis[6-7]推导出圆管结构中波的传播，为后面的学者提供了理论依据。Elvira-Segura 等[8]研究了声波在充满黏性液体的圆管结构中的频散特性。Aristegui 等[9]研究了内外表面由不同液体包围的铜管结构中导波的传播特性。Sun等[10]研究了圆管中非对称扭转导波传播机理以及激励方法。Davies等[11]从实验以及有限元仿真两方面将合成聚焦成像的方法引入到管道损伤检测中。Clarke 等[12]研究了基于导波、稀疏阵列结构健康监测系统在变温度状态的复杂结构损伤诊断方面的评估。Lee等[13]使用激光激励，对碳钢管进行腐蚀检测以及状态评估。Demma 等[14]分析了管中槽损伤反射导波及其应用。他得安等[15-16]对充满黏性液体管材中超声导波的应力进行了分析，并在此基础上讨论各个模态的最佳频厚积选择范围及检测位置。文献[17-18]对弯管道损伤检测进行了仿真以及导波传播特性研究。孔维梁等[19]对带有黏性液体的圆柱、圆管的扭转模态导波的传播特性进行了研究，获取了黏性、密度等和第1阶扭转模态之间的关系。耿艳峰等[20]采用了基于子波估计的反褶积技术处理管道导波测量数据，有效地抑制导波频散，提高了管道损伤检测的定位精度。

笔者通过管中导波的频散特征、波的结构等方面因素选择激励信号，通过有限元仿真验证圆管中导波的传播机理。提出基于椭圆法的圆管损伤定位，并通过在圆管上引入切槽损伤、孔损伤进行验证，并对损伤大小、位置对定位误差的影响进行了分析。

1 管中导波特性及激励信号选择

根据导波传播方向不同，圆管中的导波可分为纵向导波与周向导波两大类，前者沿圆管轴线方向传播，后者沿圆周环绕传播。根据波的结构，纵向导波可分为纵向模态、扭转模态与弯曲模态，周向导波可分为管周向SH波与管周向Lamb波。扭转模态与周向SH波都是剪切波，前者需在管的某一截面整周激励才能激发，而后者需在整个内表面或者整个外表面激励。弯曲模态导波模式成分较多，频散特征比较复杂，限制了其在结构健康监测中的应用。所以基于超声导波的管道结构健康监测，通常选用纵向导波模态以及周向Lamb波。

1.1 导波频散曲线

Gazis根据Navier控制方程、本构方程、广义胡克定律以及应力边界条件，推导出管中纵向导波频散方程为

=0 (i=1,2,…,6;j=1,2,…,6)

(1)

ci,j与圆管几何尺寸(内圆半径a及外圆半径b)、材料属性(弹性模量E、泊松比ν及密度ρ)有关，其详细表达式见文献[6-7]，通过此方程可以得到频率f与相速度cp之间的关系。相速度与群速度满足

(2)

由频率f与相速度cp，即可求得频率f与群速度cg之间的关系。

管中周向Lamb波的频散方程为

=0 (i=1,2,3，4；j=1,2,3,4)

(3)

Di,j与圆管几何尺寸、材料属性、频率f与相速度cp有关，其表达式见文献[21]。

根据式(1)～式(3)，利用数值法求解该两种模态，可求解的频率范围为0～1 000kHz，相速度在10km/s以内。内径为174mm、外径为194mm、材料为20#碳钢(E=208 GPa，ν=0.28，ρ=7 800kg/m3)的相速度、群速度与频率之间的关系分别如图1和图2所示。

由图1与图2可得，管中纵向模态导波与周向Lamb波在低频阶段明显不同，高频阶段收敛情况也不一致。L(0,2)模式与周向Lamb波第2个模式，在50 kHz～150 kHz频段群速度最快，导波成分比较简单，频散程度最小，同时群速度曲线比较平缓，所以优先考虑此频率范围。笔者选取中心频率为80 kHz的激励信号，以此频率激励，纵向模态与周向Lamb波都只有两种模式被激励，波的成分相对简单，便于数据处理。此时L(0,1)模式与L(0,2)模式的群速度分别为3 147 和5 275 m/s，以及周向Lamb第1个、第2个模式的群速度分别为3 340 和5 498 m/s。

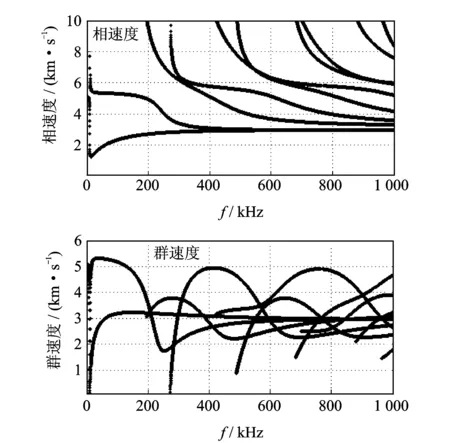
图1 圆管纵向模态导波频散曲线Fig.1 Pipe′s longitudinal modes guided-wave dispersion curves

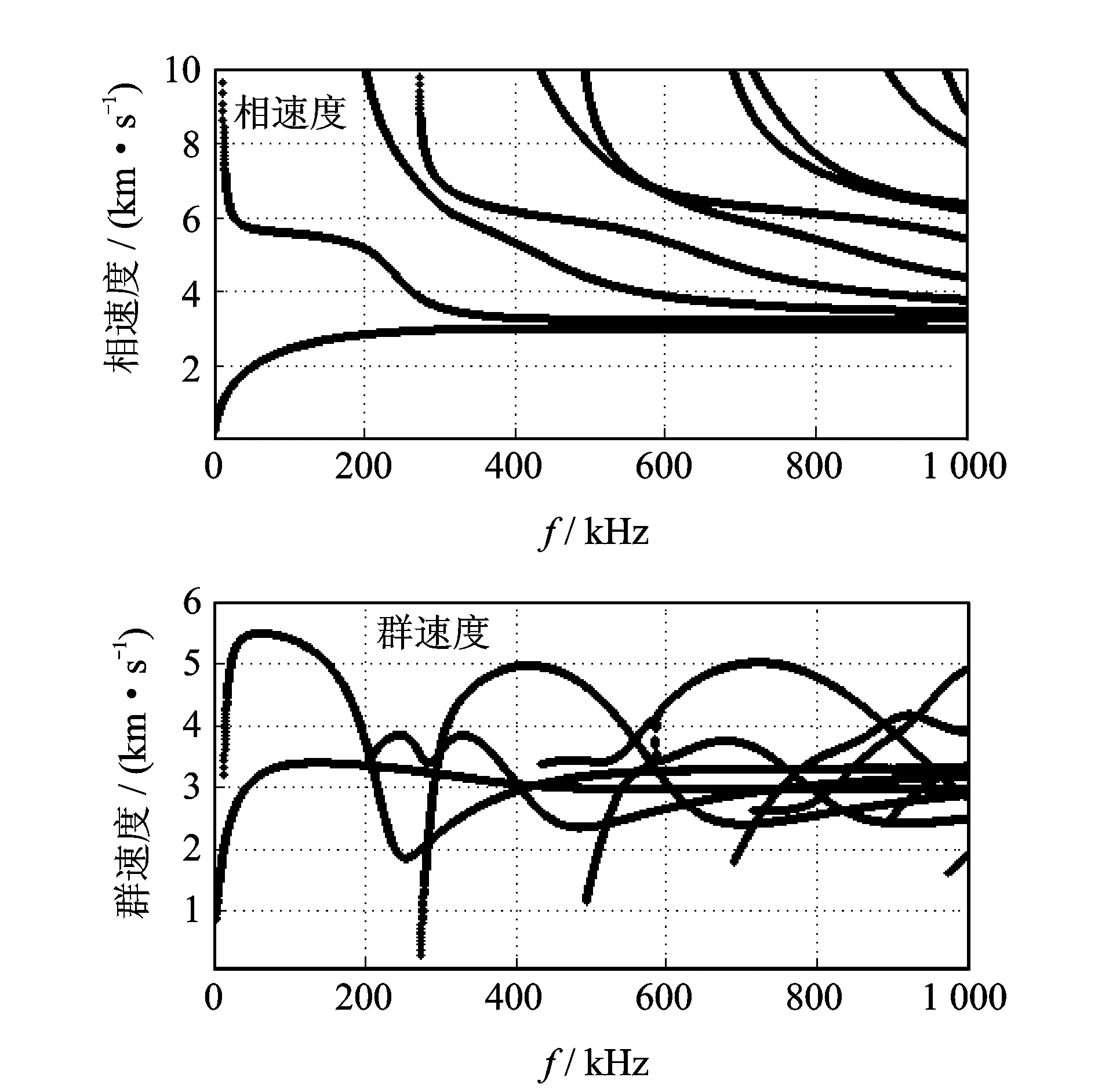
图2 圆管周向Lamb波频散曲线Fig.2 Pipe′s circumferential Lamb wave dispersion curves

1.2 波的结构

波的结构是指各模式导波沿各个方向的位移分量。波的结构在一定程度上影响波在传播过程中的能量泄露情况。如果径向位移比较大，会引起周围介质的振动，则波在传播过程中幅值衰减比较快，导致难以远距离传播与信噪比降低。结合导波的频散特性以及波的结构，正确选择导波模式有利于实现损伤检测。

激励频率为80 kHz时，圆管L(0,2)模式导波与周向Lamb波第2个模式导波在各个方向的位移幅值分布如图 3所示。其中：横坐标为距圆管轴心的距离；红色实线与红色虚线分别代表L(0,2)模式的面内位移(轴向位移)分量幅值与离面位移(径向位移)分量幅值；黑色实线与黑色虚线分别代表周向Lamb波第2个模式的面内位移(轴向位移)分量幅值与离面位移(径向位移)分量幅值。由图3可知，该圆管中周向Lamb波的结构与L(0,2)模式波的结构比较接近。离面位移分量比面内位移分量小很多，使得波在传播过程中能量泄漏比较小，能够实现远距离传播。周向Lamb波的第2个模式以及L(0,2)模式导波的面内位移(轴向位移)分量，随着距圆管轴心距离的变化，其相对大小改变不大，因而对于圆周任何位置，其检测的灵敏度比较接近，能够实现整个截面的损伤检测。

图3 波的结构Fig.3 Wave structure

2 仿真与实验

2.1 有限元模型

在ABAQUS软件平台上选用三维实体8节点缩减积分单位(C3D8R Element)，采用Explicit求解器，进行动态有限元分析，对上述圆管导波的传播特性进行仿真。该方法能够较准确地求解弹性应力波的传播。

在对导波传播进行有限元仿真过程中，为了保证模拟相应导波波长在传播过程中的控件迭代产生的误差较小，减少由于网格划分引起的误差，甚至计算结果发散，每个波长上至少需划分7个网格[22-23]

λmin≥7Δxmax

(4)

其中：λmin为最小波长；Δxmax为最大网格尺寸。

在此仿真过程中，最大的网格尺寸为2.5mm，而激励频率为80kHz时，最小波长接近39mm，满足式(4)。

仿真过程中，每增加时间Δt，新进入网格的计算区域应大于导波增加的传播范围。为了使算法稳定，需限定计算的时间步长，其大小[22]需满足

cLΔt≤Δxmin

(5)

在此仿真中，时间步长为1.0×10-8s，最小网格尺寸为1mm，得到纵波波速小于100km/s，满足要求。

在图 4中A处模拟一个20 mm×5 mm×1 mm的压电应变片(piezoelectric transducer，简称PZT)，通过施加集中力模拟PZT通电后由于逆压电效应产生应力、应变，在S1，S2处模拟PZT接收的信号。其中：S1与A在圆管同一个横截面上，相距半个圆周；S2与A在圆管外圆同一条外圆母线上，相距0.3 m。在A处用经过汉宁窗调制的3.5个周期的80 kHz施加集中载荷激励，导波传播情况如图5所示。

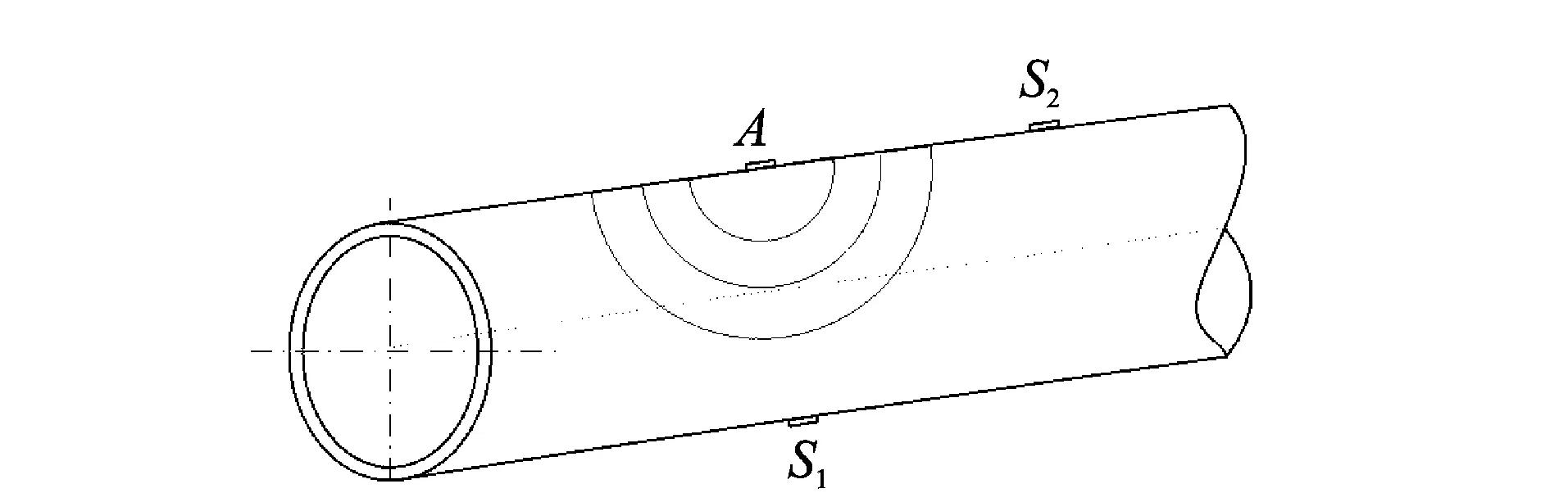
图4 驱动器与传感器布置Fig.4 Actuator and sensors distribution

图5 不同时刻导波传播情况Fig.5 Guided wave propagation at different time

S2除了能够接收到纵向模态导波外，还能够接收环绕周向传播的周向Lamb波。在经圆管端部反射的导波到达S1前，各个波包到达S1的时间为

t=(2n-1)πb/cg(n=1,2,…)

(6)

其中：b为外圆半径；cg为各周向Lamb波群速度。

S1与S2两处接收的应力波信号如图6所示。Heisenberg等[24]用“波包的速度”解释群速度，通过使用希尔伯特变换求取其波包包络线。

离散时间信号序列x(n)经希尔伯特变换后为

(7)

包络信号序列e(n)为

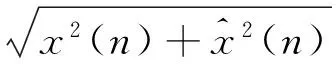
(8)

由图6可得，周向Lamb波第1个与第2个模式的波包到达S1的时间分别为93.2和56.7 μs，由图2可得两者的群速度分别为3 340和5 498 m/s，驱动器与传感器之间的距离(飞行距离)为304.7 mm，所以驱动器开始激励信号到传感器开始接收信号之间的飞行时间为91.2和55.4 μs，误差较小。

同样由图6可得，L(0,1)与L(0,2)两个波包到达S2的时间分别为96.5和55.1 μs。而由图2可得，L(0,1)模式与L(0,2)模式导波的群速度分别为3 147和5 275 m/s，飞行距离为300 mm，所以飞行时间分别为95.3和56.9 μs，误差同样非常小。

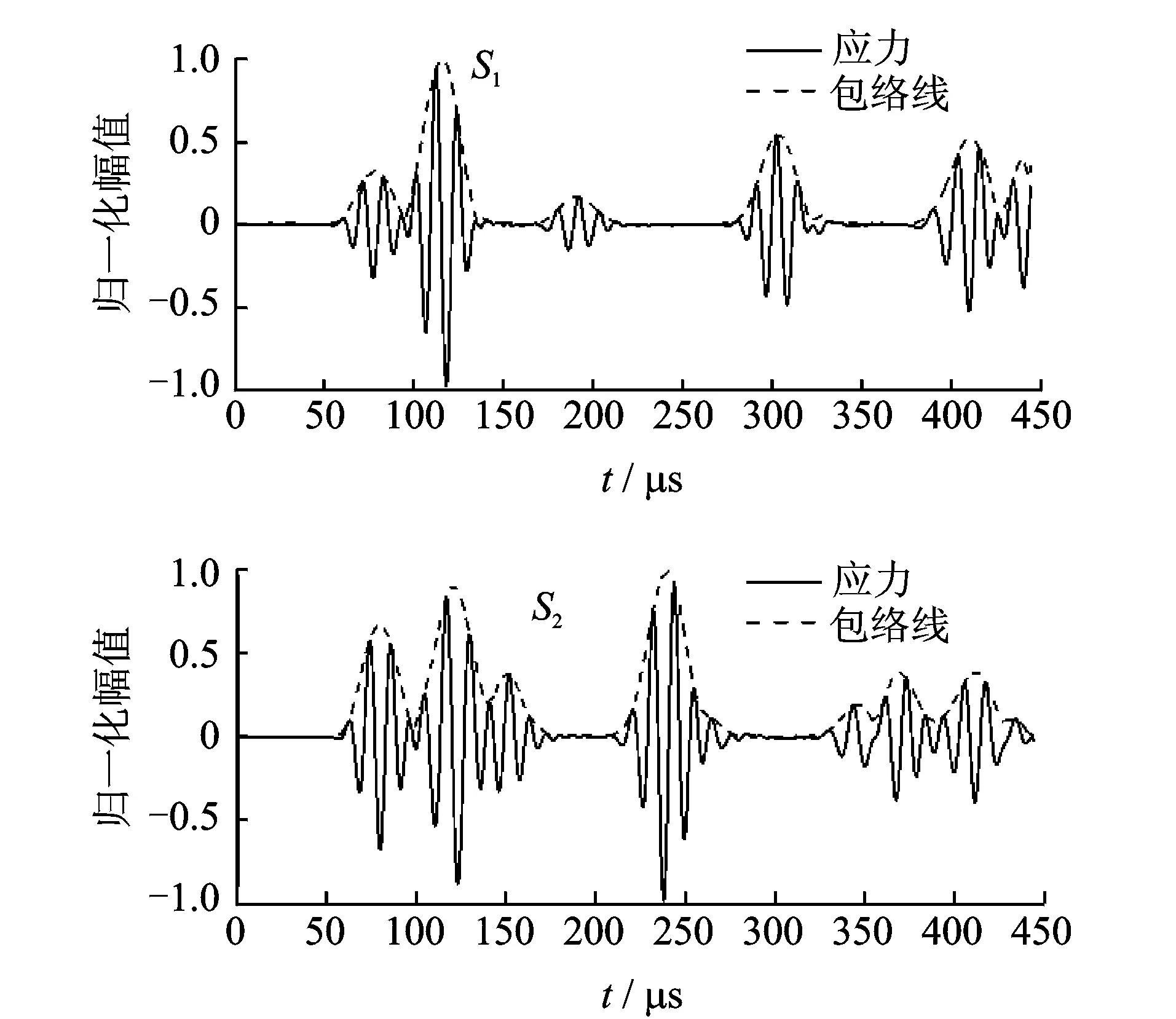
图6 应力及其包络线Fig.6 Stress and its envelope

2.2 椭圆法定位损伤

图7 圆管导波传播展开示意图Fig.7 Unfolded diagram of pipe′s guided wave propagation

由图5可得，纵向导波沿轴线传播，周向导波绕圆周传播，两种导波相互耦合。在80 kHz激励频率下，产生L(0,1)与L(0,2) 两个纵向模态导波，以及两个周向模态导波。由于纵向导波L(0,1)与L(0,2)模态与周向导波第1、第2模态的群速度比较接近，在最初阶段，如果将圆管展开为一个平面，导波传播形式可近似为两个同心圆。由于圆管结构的特殊性，周向导波绕圆周传播，时间较长时，由于导波绕圆管传播，所以将圆管展开后导波的传播虽可近似为圆弧，但只有一部分以驱动器所在位置为圆心，如图7所示。图7(b)中，上面与下面的两条实线圆弧不是“到达边界”后的反射波，而是由于在圆管结构中，波传播半个圆周后绕另半个圆周传播，即上、下大圆弧分别是展开示意图下部分、上部分的延伸。

由图2可得管中的纵向模态导波以及周向Lamb波的频散特征，都与板中的Lamb波的频散特性非常相似。当频率为80 kHz时，L(0,2)模式与周向Lamb波的频散特征相似度高，群速度比较接近，分别为5 275和5 498 m/s，取其平均值5 386.5 m/s(与两个群速度相差约2%)，将圆管展开近似处理，导波从驱动器激励传播到损伤，再传播到传感器，如图8所示。

由于损伤早期时候尺寸较小，通过传感器接收的导波信号变化不大，损伤信号可能被湮没，难以定位损伤位置，所以将待检测圆管结构的导波信号与无损伤的圆管结构导波信号作差，由差信号得到损伤信号的第1个波包飞行时间，由此得到飞行距离，即驱动器产生的信号传播到损伤处、再由损伤处产生、反射或透射的信号传播到传感器所在位置经历的总距离，由此得到损伤位置到驱动器以及传感器的距离之和。得到损伤位置位于以驱动器与传感器为焦点的椭圆轨迹上。布置3个传感器，这3个传感器与驱动器不能在同一平面，可得到3个椭圆轨迹的交点，即损伤所在的位置。

通常3个椭圆没有共同焦点，主要有以下原因：a.无论仿真还是计算，都难以得到准确的波包起点，由此直接引起飞行距离误差；b.传感器、驱动器接收、发出的信号都不是集中的点信号，而是接收或发出一定区域内的信号；c.损伤通常不是一个单点，往往是一定区域内，损伤具有一定的外形轮廓，损伤处各点对传感器都有影响。由于这些原因，损伤信号最直观的表现就是时域波形变宽，引起寻找损伤信号的起始点的误差增加。因此，损伤区域比较大，则损伤定位的误差就可能会增加；但是损伤区域较小时，会引起信噪比降低，损伤信号可能被噪声信号湮没。

图8 椭圆定位示意图Fig.8 Diagram of elliptical localization

由于圆管轴对称，导波可以绕周向一直传播，得到损伤轨迹不同于板结构。根据前面方法所求得损伤椭圆轨迹方程，有可能超出圆管展开范围。当导波在驱动器所在位置激发、经损伤传播到传感器的周向飞行距离大于圆管半周长时，则可能存在多条损伤轨迹，如图9所示。

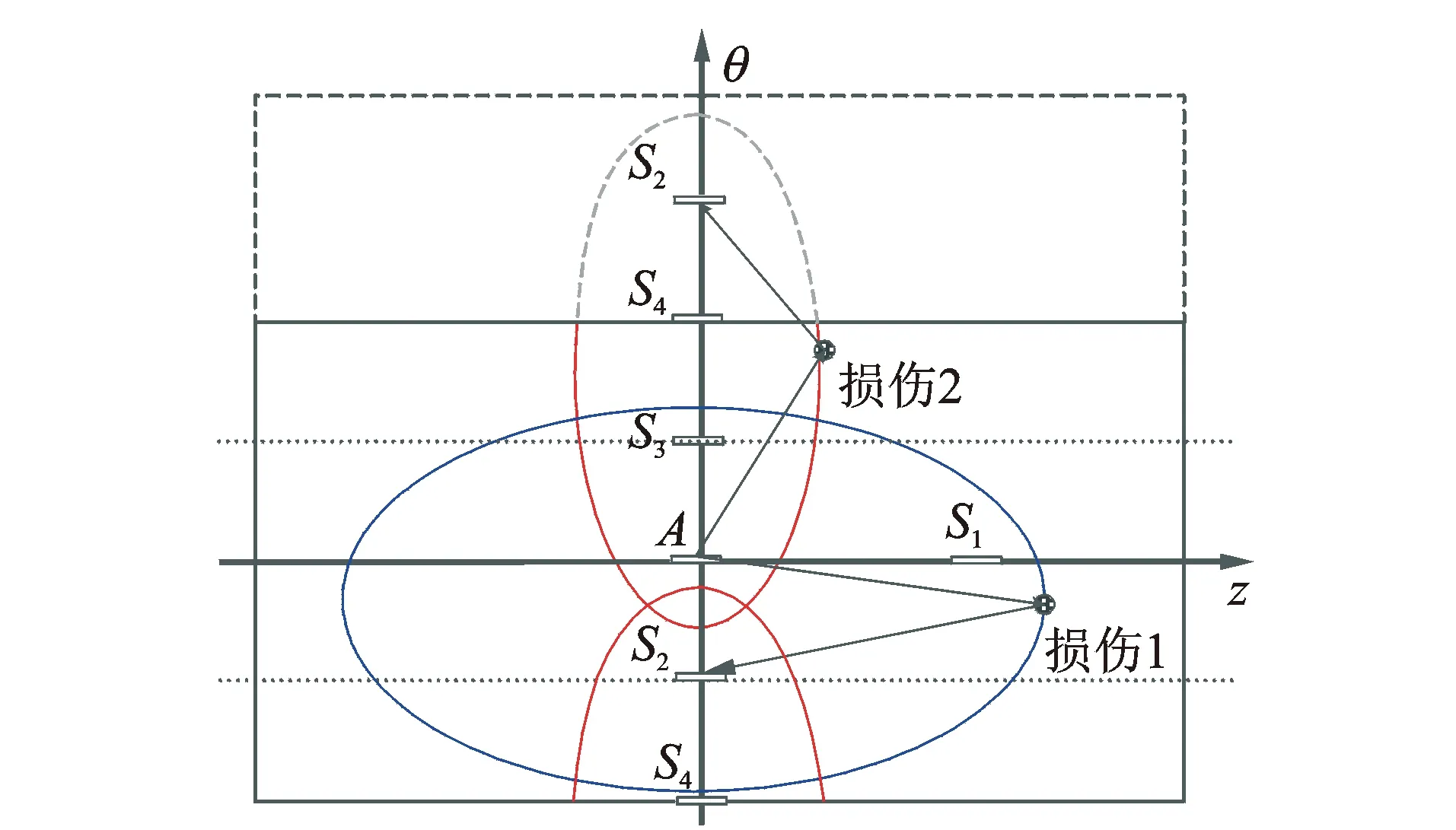
图9 多条损伤轨迹案例Fig.9 Example with multi damage-trajectories

图10 损伤大小及位置示意图Fig.10 Diagram of damage size and location

2.3 仿真算例

如图 10所示，钢管的长度为2 m，外径为194 mm，厚度为10 mm，材料为20#碳钢。在与驱动器A轴向距离为400 mm、周向30°处引入一个切槽损伤，槽宽度为1 mm，周向跨度为30°，传感器S1与切槽的轴向距离为300 mm，在驱动器所在的截面每隔90°，均布3个传感器S2，S3和S4。

采用经过汉宁窗调制的3.5个周期80 kHz正弦信号在A处激励。由于引入切槽损伤后的应力大小与无损圆管差异不大，所以分别将对应的测点有无损伤的应力相减得到差信号，如图 11所示，以此由损伤引起的导波传播差异，作为依据判断损伤所在的位置。

由图 11可得，S1，S2和S3这3个测点的第1个波包到达的时间比较早，第1个波包到达S4的时间最晚，所以损伤距S4的距离最远。S1，S2和S3所接收的损伤信号的第1个波包起始时刻分别为131.5，151.8和159.6 μs，取波速为L(0,2)与周向Lamb波第2个模态的平均群速度5 386.5 m/s，由此得到飞行距离分别为708.3，817.7和859.7mm。结合驱动器A所在位置，得到3个椭圆轨迹E1，E2和E3。3个椭圆没有共同交点，但有两两相交，并且有3个点的位置非常接近，都在驱动器A的右侧，与A的轴向距离分别为402.5，397.9和392.3 mm，平均为397.6 mm。与A的周向角度分别为44.9°，23.6°和25.3°，平均为34.6°。轴向定位误差比较小，周向定位误差较大。

为了评估该方法的效果，验证其周向定位以及周向定位的效果，分别设计了6个切槽损伤算例与6个孔损伤算例。轴向定位误差较小，而周向定位误差一般比轴向定位误差大，其周向定位结果如表1及表2所示。其中:(20°，30°)表示在圆管30°处有一弧长为20°的槽损伤;(∅5，30°)表示在圆管30°处有一直径为5 mm的孔损伤。

图11 差信号及其包络Fig.11 Difference signals and their envelopes

表1 带槽损伤的圆管及损伤周向定位

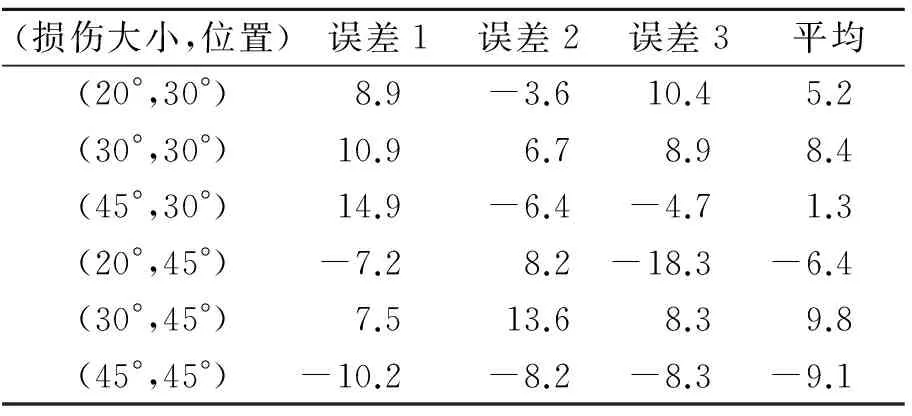
Tab.1 Pipe with notch and damage circumferential localization (°)

表2 带孔损伤的圆管及损伤周向定位

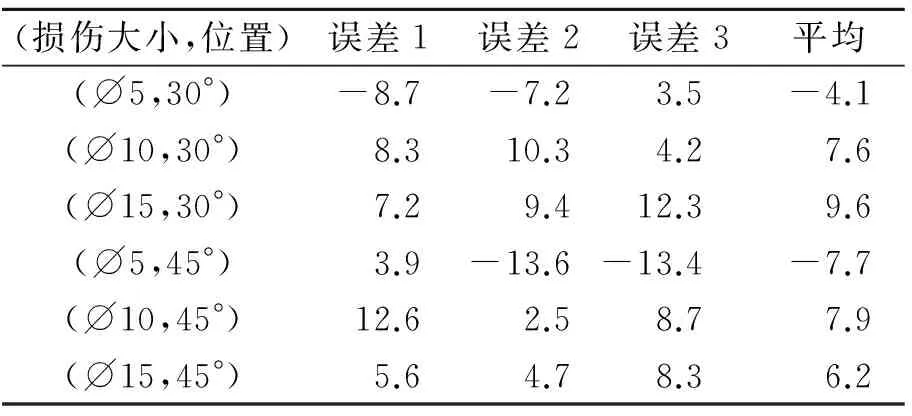
Tab.2 Pipe with hole and damage circumferential localization (°)

从表1和表2可知，周向定位误差波动较大，损伤大小以及位置会影响定位误差。

2.4 实验算例

在仿真的基础上进行实验验证。本研究采用PZT压电陶瓷晶片。实验现场如图12所示，由型号为TEKAFG3022B的信号发生器产生激励信号。将该信号分成两路，一路直接连接示波器以作参考信号，用来判断零时刻；另一路经过型号为KH 7602M的功率放大器将信号幅值放大，再通过PZT晶片将电信号转换为机械信号，在检测结构中产生导波。由PZT晶片将机械信号转换为电信号，最后通过型号为DPO 3014的示波器显示、平均化处理、保存导波响应波信号，以供后期信号处理，实现损伤的识别与定位。

图12 实验现场Fig.12 Experimental sense

仿真所得到的导波响应信号，无背景噪声，可通过求取波包的包络线获取不同模式、不同传感路径的导波的传递情况。实际实验中，由于受电磁干扰、背景噪声、传感器与驱动器的安装误差等方面影响，使得实验所得的导波响应信号与仿真信号存在一定差异。使用示波器内嵌的多次平均功能，多次采样后平均处理，减小随机噪声的影响，最后通过小波变换重构采集的信号进行分析。

布置如图8所示的传感网络，取各传感器采集的512组信号的平均值经过小波变换重构，作为损伤检测的参考信号。在驱动器周向距离30°、轴向距离为400 mm处加工一个弧度为30°的槽损伤，进行如图12所示实验。同样取各传感器采集信号的512组的平均值经过小波变换重构，以二者的差信号采用上述方法进行损伤定位，损伤定位为(425,45)，轴向定位绝对误差为25 mm，相对误差为2.5%；周向定位误差为15°，相对误差约为4.2%。周向相对误差比轴向相对误差大。

3 定位误差的影响因素

影响定位精度的因素比较多：a.波包的实际起始时刻幅值比较小，导致波包起始点的选择存在一定的误差；b.不同模式的波包时域信息可能相互重合，通过波包幅值的极值点难以准确获得波包的起始时刻；c.仿真过程中由于网格划分以及时间步长设置引起的计算误差；d.激励的信号源不是点信号，而是由一个具有一定面积的驱动器激励。此外，该方法原理会导致损伤大小、损伤与传感器之间的轴向距离都会影响损伤定位结果。

3.1 损伤大小对损伤定位的影响

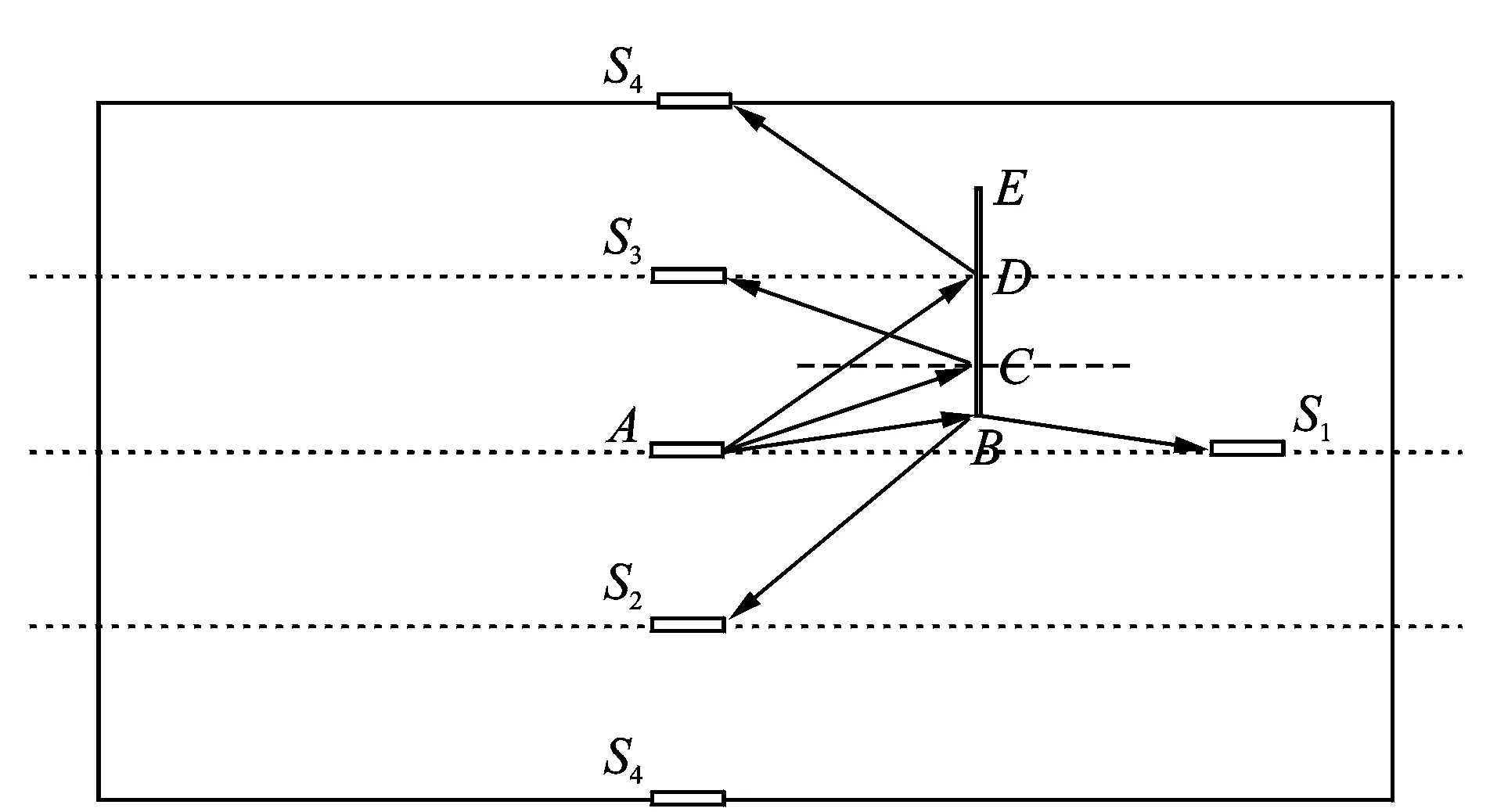
图13 损伤大小对损伤定位的影响Fig.13 Effect of damage size to its localization

损伤的大小也影响损伤定位误差。如图13所示，损伤大小不同时，损伤各点对传感器的影响权重也不一样。对于传感器S1，如果损伤经过A与S1的连线，对传感器接收的信号影响最大；如果损伤不经过A与S1的连线，随着与连线的距离增加，对传感器影响降低，同时损伤与交点最近的点对传感器影响最大。对于传感器S2，S3和S4，如果传感器与驱动器的中垂面经过损伤，则交点处的损伤对相应传感器的影响最大，交点外的损伤随着与交点距离增加对相应传感器的影响降低；如果损伤不经过传感器与驱动器的中垂面，则距离交点最近的损伤对相应传感器影响最大。同样，圆孔损伤的大小也会影响定位误差。

即使损伤的位置相同，如果损伤大小不同，导致各点在传感器处的影响也不一样，使得信号加权后得到损伤的位置与损伤实际中心位置不重合，导致难以直接通过传感器接收的信号反推来精确获得损伤位置。

3.2 周向距离对损伤定位的影响

首先讨论周向距离对角度的影响。

如图14所示，两个传感器与损伤之间的夹角满足式(9)和式(10)。

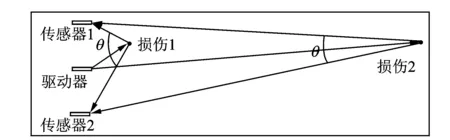
图14 损伤周向距离对损伤定位的影响Fig.14 Effect of damage axial distance to its localization

损伤位于两个传感器所在外圆母线范围内

(9)

损伤位于两个传感器所在外圆母线范围外

θ=arctan(cd/(d2+c1c2))

(10)

其中：c1和c2分别为两个传感器与损伤之间的周向距离；c为两个传感器之间的周向距离；d为传感器与损伤之间的轴向距离。

2) 当轴向距离d较小时，即d≪min{c1，c2}，此时θ≈π-dc/(c1c1)(损伤在两传感器所在母线范围内)或θ≈dc/(c1c1)(损伤在两传感器所在母线范围外)，此时损伤所在横截面与传感器所在横截面比较接近，θ的大小对c1和c2的大小较敏感；

3) 在其他情况下，θ的大小与c1和c2有关，且它们之间关系较复杂。

下面讨论周向距离对传播距离的影响。

损伤与传感器(或驱动器)之间的周向距离由c变为c+Δc时，损伤与传感器(或驱动器)之间的距离的改变量ΔD为

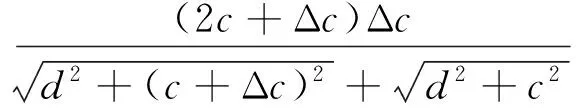
(11)

其中：d为损伤与传感器(或驱动器)之间的轴向距离。

当轴向距离远大于周向距离时，即d≫max{c,Δc}，此时ΔD≈cΔc/d，损伤与传感器(或驱动器)之间距离变化很小，波包飞行时间变化不大；而当d比较小时，Δc对ΔD影响较大。

由式(9)～式(11)可得，随着损伤位置到传感器(或驱动器)的周向距离增加，损伤的周向位置对传感器的影响就会相应地减弱;而当损伤到传感器的轴向距离比较小时，周向位置对传感器接收的信号将产生明显的影响。

4 结 论

1) 本研究通过数值法，得到管中纵向模态导波以及周向Lamb波在低频阶段以及高频收敛情况不一致。第2个模式存在一段频散较小、群速度最快、径向位移小、轴向及周向位移变化小的频率范围，管道结构健康监测激励频率应优先选择此范围。

2) 单点激励时，管道中同时存在纵向导波以及周向Lamb波两种模态，前者沿圆管轴向传播，后者绕圆管周向传播，两种波相互耦合。

3) 经过有限元仿真，采用单点激励、多点接收，应用椭圆定位法，能够较准确地实现圆管的损伤的定位，轴向定位误差较小，周向定位误差较大。

4) 损伤轴向位置、损伤大小都会对损伤定位误差产生影响。

[1] Raghavan A, Cesnik C E S. Review of guided-wave structural health monitoring[J]. Shock and Vibration Digest, 2007, 39(2): 91-116.

[2] Li Fucai, Murayama H, Kageyama K, et al. Guided wave and damage detection in composite laminates using different fiber optic sensors[J]. Sensors, 2009, 9(5): 4005-4021.

[3] Na W B, Kundu T. Underwater pipeline inspection using guided waves[J]. Journal of Pressure Vessel Technology, 2002, 124(2): 196-200.

[4] 于保华, 杨世锡, 甘春标. 一种多层圆管纵向导波频散特性分析方法研究[J]. 工程力学, 2012, 30(4): 373-379.

Yu Baohua, Yang Sixi, Gan Chunbiao. Research of frequency dispersion characteristic of longitudinal guided wave in multi-layer tube[J]. Engineering Mechanics, 2012, 30(4): 373-379.(in Chinese)

[5] 孙凯, 孟光, 叶林, 等. 基于超声导波的钢梁结构损伤大小识别研究[J]. 振动与冲击, 2011, 30(9): 227-231.

Sun Kai, Meng Guang, Ye Lin, et al. Damage size identification of thick steel beam based on ultrasonic guided wave[J]. Journal of Vibration and Shock, 2011, 30(9): 227-231. (in Chinese)

[6] Gazis D C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. I. analytical foundation[J]. The Journal of the Acoustical Society of America 1959, 31(5): 568-573.

[7] Gazis D C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. II. numerical results[J]. The Journal of the Acoustical Society of America 1959, 31(5): 573-578.

[8] Elvira-Segura L. Acoustic wave dispersion in a cylindrical elastic tube filled with a viscous liquid[J]. Ultrasonics, 2000, 37(8): 537-547.

[9] Aristegui C, Lowe M J S, Cawley P. Guided waves in fluid-filled pipes surrounded by different fluids[J]. Ultrasonics, 2001, 39(5): 367-375.

[10]Sun Zongqi, Zhang Li, Rose J L. Flexural torsional guided wave mechanics and focusing in pipe[J]. Journal of Ppressure Vessel Technology, 2005, 127(4): 471-478.

[11]Davies J, Cawley P. The application of synthetically focused imaging techniques for high resolution guided wave pipe inspection[C]∥Review of Progress in Quantitative Nondestructive Evaluation. America：AIP Publishing, 2007: 681-688.

[12]Clarke T, Cawley P, Wilcox P D, et al. Evaluation of the damage detection capability of a sparse-array guided-wave SHM system applied to a complex structure under varying thermal conditions[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2009, 56(12): 2666-2678.

[13]Lee J H, Lee S J. Application of laser-generated guided wave for evaluation of corrosion in carbon steel pipe[J]. NDT & E International, 2009, 42(3): 222-227.

[14]Demma A, Cawley P, Lowe M, et al. The reflection of guided waves from notches in pipes: a guide for interpreting corrosion measurements[J]. NDT & E International, 2004, 37(3): 167-180.

[15]他得安. 充粘性液体管材中超声导波的应力分析[J]. 声学技术, 2006, 25(5): 419-425.

Ta Dean. Stress analysis of ultrasonic guided waves in viscous liquid-filled pipes[J]. Technical Acoustics, 2006, 25(5)：419-425.(in Chinese)

[16]他得安, 刘镇清, 贺鹏飞. 充粘液管材中超声纵向导波的无损检测参数选择[J]. 声学学报, 2004, 29(2): 104-110.

Ta Dean, Liu Zhenqiang, He Pengfei. Optimal parameters of ultrasonic guided waves non-destructive testing in viscous liquid-filled elastic pipes[J]. Acta Acustica, 2004, 29(2): 104-110. (in Chinese)

[17]何存富, 孙雅欣, 刘增华, 等. 弯管缺陷超声导波检测的有限元分析[J]. 北京工业大学学报, 2006, 32(4): 289-294.

He Cunfu, Sun Yaxin, Liu Zenghua, et al. Finite element analysis of defect detection in curved pipes using ultrasonic guided wave[J]. Journal of Beijing University of Technology, 2006, 32(4): 289-294. (in Chinese)

[18]王秀彦, 刘增华, 孙雅欣, 等. 弯管中超声导波传播特性的研究[J]. 北京工业大学学报, 2006, 32(9): 773-777.

Wang Xiuyan, Liu Zenghua, Sun Yaxin, et al.Research on the guided propagation characteristics of ultrasonic guided waves in curved pipes[J]. Journal of Beijing University of Technology, 2006, 32(9): 773-777. (in Chinese)

[19]孔维梁, 周丽, Fuh-Gwo Y. 粘性液体对管道中扭转导波传播特性的影响研究[J]. 振动与冲击, 2012, 31(11): 48-53.

Kong Weiliang, Zhou Li, Fuh-Gwo Y. Influence of viscous liquid on propagation of torsional wave in a pipe[J]. Journal of Vibration and Shock, 2012, 31(11): 48-53. (in Chinese)

[20]耿艳峰,王丹,华陈权. 基于反褶积与编码激励的长输管道损伤检测[J]. 振动、测试与诊断,2014,34(1):130-135.

Geng Yanfeng, Wang Dan, Hua Chenquan. Based on the deconvolution and coding incentive long-distance pipeline damage detection[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(1):130-135. (in Chinese)

[21]Rose J L. Ultrasonic waves in solid media[M]. [S.l.]:Cambridge University Press, 2004: 125-142.

[22]杜修力. 工程波动理论与方法[M]. 北京：科学出版社, 2009: 72-142.

[23]Diligent O, Grahn T, Boström A, et al. The low-frequency reflection and scattering of the S0 Lamb mode from a circular through-thickness hole in a plate: finite element, analytical and experimental studies[J]. The Journal of the Acoustical Society of America, 2002, 112(6): 2589-2601.

[24]Serway R, Jewett J. Physics for scientists and engineers[M]. [S.l.]:Cengage Learning, 2013:449-499.

10.16450/j.cnki.issn.1004-6801.2017.03.004

国家自然科学基金资助项目(11372179)；教育部新世纪优秀人才资助项目 (NCET-13-0363)

2015-04-08；

2015-06-11

TH113.1； TB559

王国锋，男，1991年1月生，硕士。主要研究方向为机械工程故障检测。

E-mail:kantwang@126.com