BP网络在进给系统定位误差预测中的运用

邓 超， 钱有胜， 吴 军， 熊 尧， 段超群

(1.华中科技大学机械学院制造装备数字化国家工程中心 武汉, 430074)(2.华中科技大学船舶与海洋工程学院 武汉,430074) (3.武汉第二船舶设计研究所 武汉,430070)



BP网络在进给系统定位误差预测中的运用

邓 超1， 钱有胜1， 吴 军2， 熊 尧3， 段超群1

(1.华中科技大学机械学院制造装备数字化国家工程中心 武汉, 430074)(2.华中科技大学船舶与海洋工程学院 武汉,430074) (3.武汉第二船舶设计研究所 武汉,430070)

针对机床进给伺服系统定位精度预测的难点，分析了进给伺服系统机械传动系统定位误差增长的原因，提出了一种定位误差预测的方法。在Adams中建立进给伺服系统动力学仿真模型,得到不同初始状态下的定位误差值，基于BP神经网络建立工作台与螺母座间隙、滚珠丝杠倾斜度、工件负载与定位误差之间的映射模型，根据映射模型提出对定位误差预测的方法。利用所建立的精密运动可靠性试验平台进行验证，证明了该方法的正确性和有效性。

进给伺服系统； BP神经网络； 映射模型； Adams；定位误差预测

引 言

定位精度是衡量数控机床性能的重要指标，根据定位精度可以判断出机床自动加工过程中能达到的最好的工件加工精度。对机床定位精度预测的研究一直受到众多学者的关注[1-4]，但是从定位精度退化原因的角度对其进行分析预测的研究较少。定位精度表示理想位置与真实位置的接近程度，能够通过定位误差计算得出。定位误差表示理想位置与真实位置的差值，能够很好地反映定位精度，易于测量，不需要复杂的数据处理过程。笔者在分析定位误差增长机理的基础上对其进行预测。

进给伺服系统定位误差主要取决于性能的优劣，受到电气伺服系统与机械特性参数的影响，其误差源包含伺服控制系统、机械传动系统、环境负载和加工载荷等。进给伺服系统定位误差检测项有轴线定位误差和机械传动系统定位误差，其中轴线定位误差包括电气伺服误差和机械传动系统误差。进给伺服系统定位误差衰退的原因可以分为3类：a.滚珠丝杠材料及尺寸、传动系统刚度、系统阻尼、工作台与螺母座间隙、滚珠丝杠倾斜度及工件负载等，称为结构与工艺参数；b.各个零部件的磨损、老化、疲劳及弯曲等，称为故障模式参数；c.位置环增益、电流环增益、速度环增益及进给率等，称为控制参数。滚珠丝杠的磨损会导致工作台与螺母座间隙增大，滚珠丝杠的弯曲会导致滚珠丝杠倾斜度增大，所以故障模式参数是通过引起结构与工艺参数变化而影响定位误差。结构与工艺参数中的系统刚度等不会有太大变化，控制参数主要对电气伺服误差产生影响，因而笔者选取结构与工艺参数中工作台与螺母座间隙、滚珠丝杠倾斜度及工件负载等，分析这些参数的变化对进给伺服系统机械传动系统定位误差的影响。

机床进给伺服系统结构与工艺参数的变化一般不容易测得，而现场数据收集环境比较复杂，受到现场加工作业状况、场地、操作条件和其他人为因素等方面的影响，因此笔者通过虚拟样机的方式对结构与工艺参数、工作台的输出进行采样，并预测定位误差。

1 机械传动系统定位误差增长机理分析

进给伺服系统机械传动系统是一个二阶系统，在扰动输入为0时，定位误差不会发生变化[5],但长时间的磨损会导致机械传动系统零部件出现间隙、倾斜和弯曲，从而引起定位误差的增大。因振动、冲击及工件负载变化对机械传动系统产生的扰动输入，也会导致定位误差的增大。假设联轴器之间的间隙、滚珠丝杠与支撑轴承之间的间隙、轴承本身间隙、滚珠丝杠与螺母座之间的间隙等均以工作台与螺母座间隙α表示，导轨的倾斜度、滚珠丝杠的弯曲度及轴承座的倾斜度等均以滚珠丝杠倾斜度β表示，因振动、冲击及工件负载变化等引起的扰动输入以工件负载F表示。机械传动系统部件与定位误差之间存在内在关系，如图1所示。

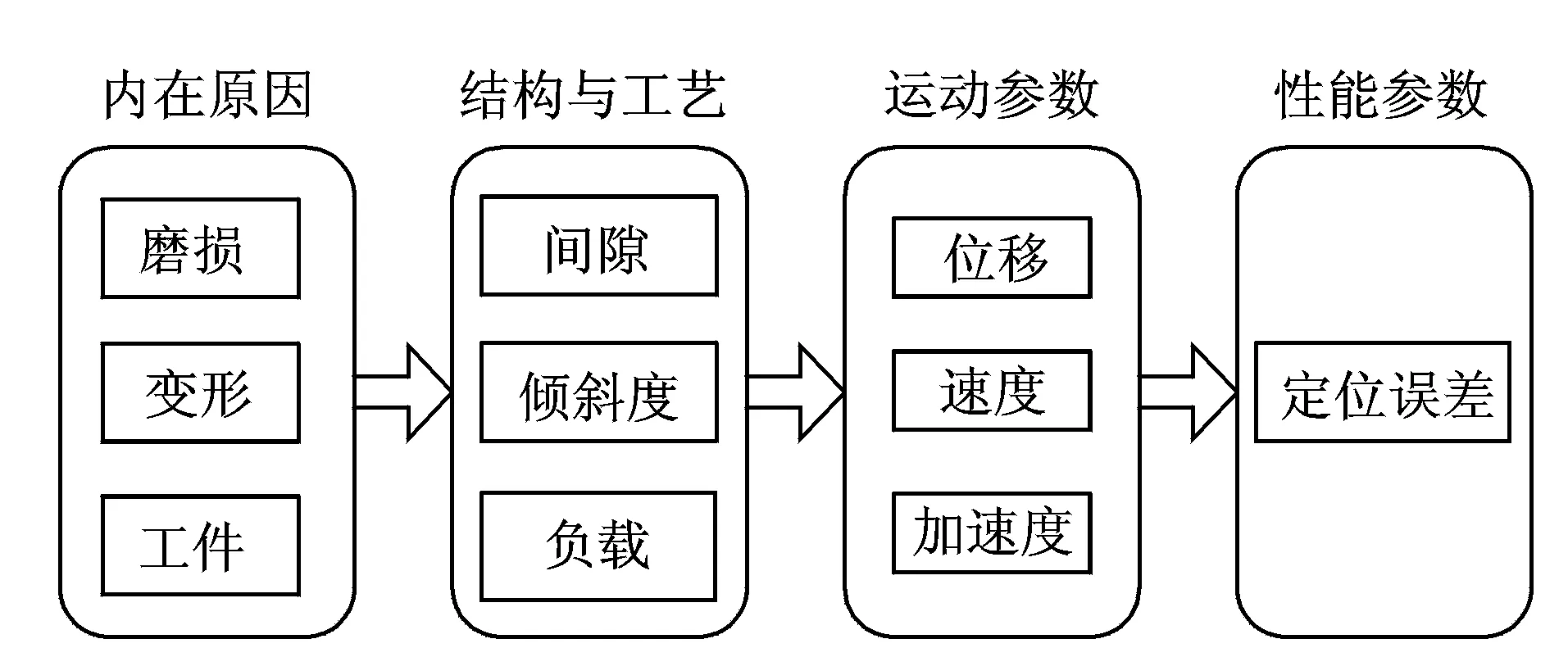
图1 机械传动系统部件与定位误差内在关系Fig.1 The intrinsic relationship between component of mechanical transmission system and positioning accuracy

设由于α,β,F而引起的定位误差为g(α,β,F)，其他因素等引起的定位误差为A0。在不考虑因腐蚀、热变形等因素导致的定位误差A增大的情况下，A的增大主要是由α,β,F的增大引起的。设A0保持不变，则机械传动系统定位误差A可以表示为

A=g1(α，β，F)=g(α，β，F)+A0

(1)

对于大多数数控机床而言，在其寿命时间里，极限加工是很少的，大部分都具有较为固定的加工零部件和工艺范围，中等工况居多。基于此，在一种工况下假设工件负载F保持不变。进给伺服系统磨损过程包括磨合阶段、稳定磨损阶段和急剧磨损阶段。在急剧磨损阶段，因磨损而引起的α，β的增大满足一定规律。β的增大主要是由于导轨副的磨损而引起的，β与直线度误差B之间满足β=arctanB。根据等价无穷小替换，当B→0时，β～B。进给伺服系统实际工作中，B与β都是在非常小的范围内变化，所以β～B。根据文献[2]，导轨副的体积磨损与滑动行程呈正比，导轨直线度B随时间t的衰减是线性的，所以β随时间t衰减也为线性关系，设为

β=f(t)=kt+b

(2)

工作台与螺母座间隙α是进给系统重要的非线性环节，α的增大主要是由于传动部件磨损而引起的[5-6]，α增大会导致反向间隙误差C增大，α与C之间近似满足α=C。假设α=h(t)，指数函数对设备的退化规律有良好的表征，因而笔者用指数函数表征α的衰减，设为

α=h(t)=a+bexp(ct)

(3)

2 进给伺服系统建模仿真

2.1 进给伺服系统建模

通过Proe(Pro/Engineer)建立数控机床进给伺服系统三维模型，如图2所示。各零件的材料、尺寸等属性均按照所建立的精密运动可靠性试验平台实际参数进行设置。

图2 进给伺服系统三维模型Fig.2 The 3D model of feed system

将模型导入Adams(automaticdynamicanalysisofmechanicalsystems,简称Adams)中，添加运动副、摩擦力和驱动力矩，具体如下:

1) 对虚拟样机添加运动副；

2) 对虚拟样机添加摩擦力以及驱动力矩，设置导轨处移动副摩擦因数为0.003，重力加速度为9 800mm/s2，x和y轴添加恒定的驱动力矩为8和45 Nmm;

3) 设置进给伺服系统x轴的间隙αx和倾斜度βx，y轴的间隙αy和倾斜度βy的初始值，用工作台垂直方向负载F表示扰动输入;

4) 添加运动副、驱动力及负载完成后，验证模型自由度个数，确保正确性。

得到进给伺服系统动力学模型如图 3所示。

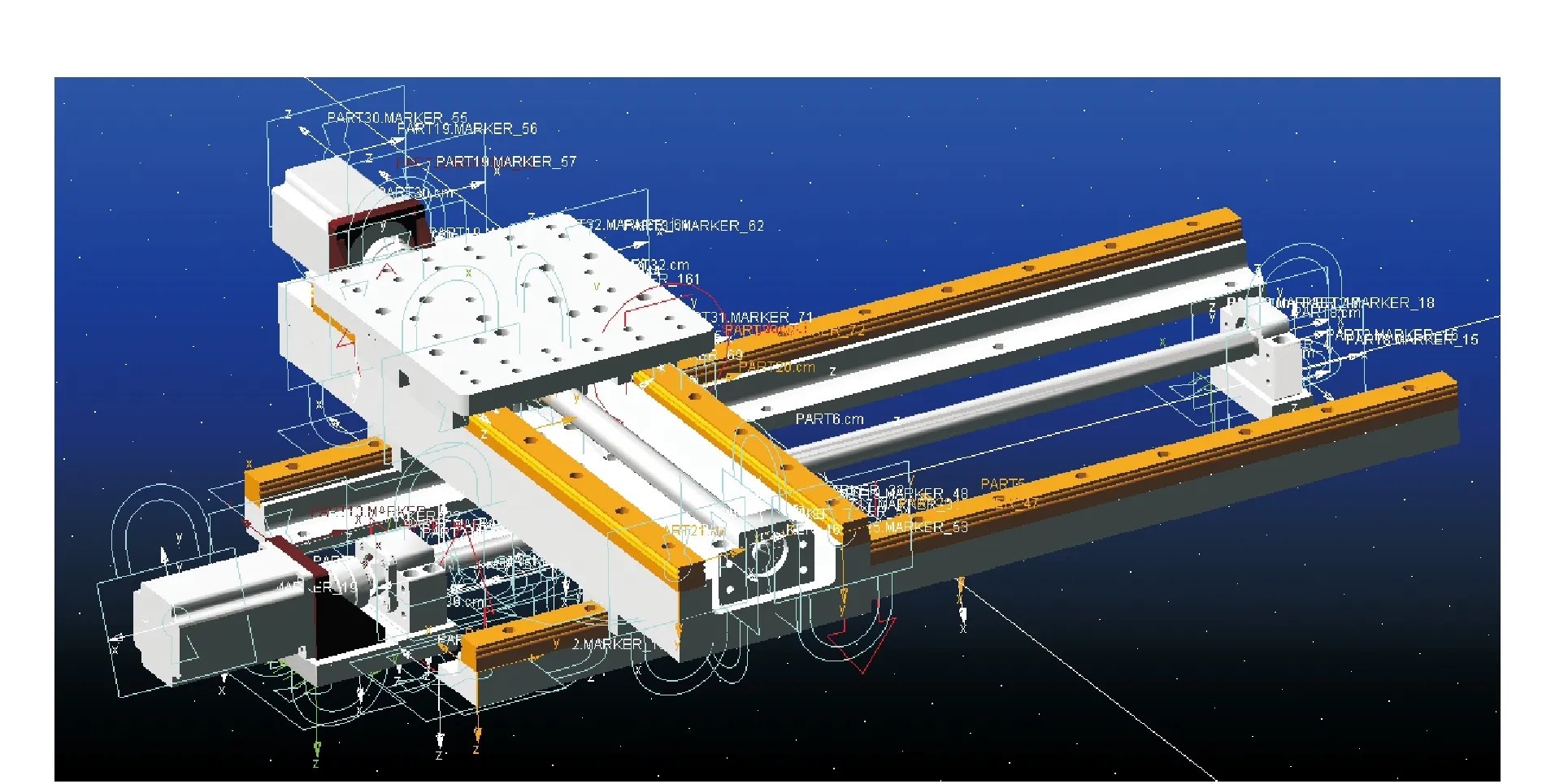
图3 进给伺服系统Adams仿真模型Fig.3 The Adams simulation model of feed system

2.2 数值仿真

设αx,αy,βx及βy为不同值， 采用控制变量法分析αx,αy,βx,βy以及F对工作台输出的影响。保持恒定的驱动力距，仿真时间为2s，步距为0.001s。设置α，β及F均为0，然后进行仿真，运动过程如图 4(a)所示，工作台位移、速度和加速度输出如图 4(b)所示。将αx,αy,βx,βy及F均为0时位移数据设为工作台第0组输出。改变αx，αy，βx，βy及F，

得到不同初始状态下的位移数据，然后与第0组输出相比较，获得x轴定位误差Ax及y轴定位误差Ay。

αx,αy,βx,βy及F取值见图4，获得55=3 125组仿真数据。

对工作台位移输出数据进行处理得到Ax和Ay，部分数据如表 1所示。

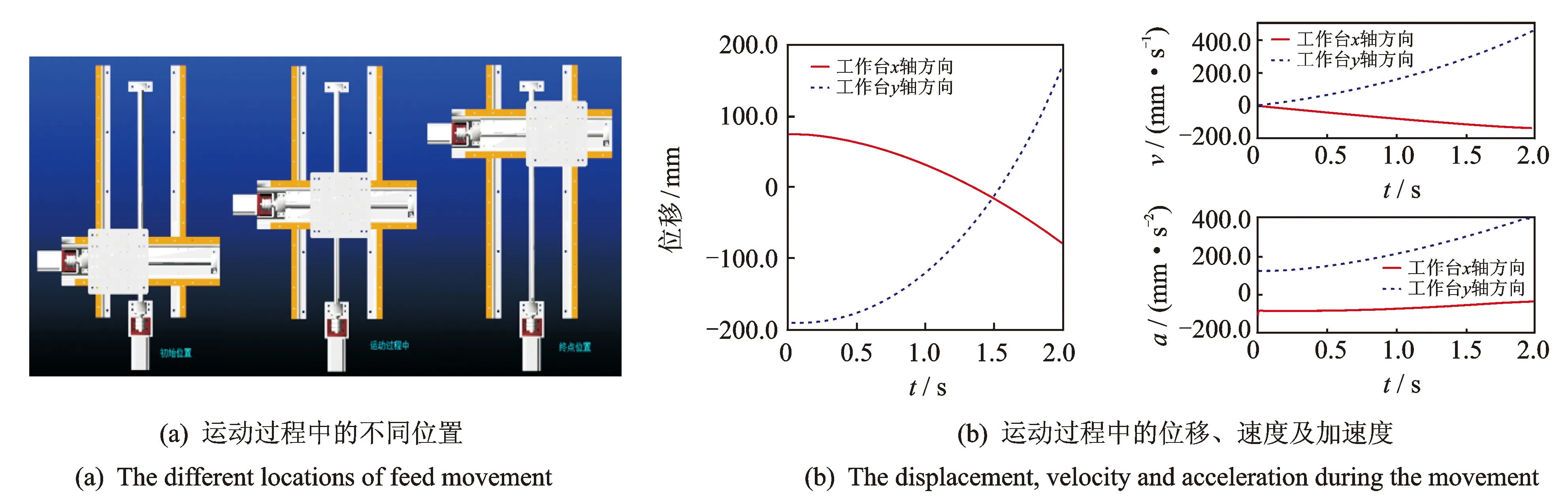
图4 运动过程的仿真Fig.4 The simulation of the movement

组号初始状态Ay/μmAx/μm0F=0N,βx=0°,βy=0°,αx=0mm,αy=0mm001F=0N,βx=0°,βy=0°,αx=0mm,αy=0.001mm0.601.12︙︙︙︙3123F=0.004N,βx=0.0004°,βy=0.0004°,αx=0.004mm,αy=0.003mm10.7021.003124F=0.004N,βx=0.0004°,βy=0.0004°,αx=0.004mm,αy=0.004mm11.1121.91

3 基于BP神经网络的映射模型

3.1 BP神经网络模型设计

设置F不变，α和β分别增加时，定位误差A成单调递增的趋势，但α，β与A之间的经验公式(1)难以确定。一个精炼的BP神经网络不需要任何先验公式，就能自动归纳已有数据的规则，获得这些数据的内在规律。神经网络被广泛应用于故障诊断、性能退化及预测[7-8]。 笔者采用BP神经网络建立α，β，F与定位误差A的映射模型，代替经验公式(1)。

BP网络的输入输出层以及隐层的确定较为关键[9]。选择αx，αy，βx，βy及F作为输入量，机械传动系统定位误差Ax，Ay作为目标输出。对于隐含层的神经元个数，不能通过理想的公式来获得，一般根据经验和多次试验来确定[10-11]。经过多次试验、调整，选择隐含层神经元个数为7个，BP网络映射模型如图 5所示。S型函数可以很好地处理和逼近非线性的输入/输出关系，所以选取S型双曲正切函数为隐含层神经元传递函数，S型对数函数为输出层神经元传递函数[12]。

图5 BP网络映射模型Fig.5 The BP network mapping model

3.2 网络训练及预测

以Adams仿真获得的前3 100组数据作为训练样本，后25组数据作为预测样本。在进行网络训练之前，利用premnmx函数对数据进行归一化处理，让输入样本和输出样本数据都处在[-1,1]或[0,1]之间[13]。样本数据归一化完成后，通过设计的模型完成对网络的训练。设定其学习训练速率η=0.025，初始权值的收敛因子ξ=1.5×10-4，并对初始权值和阈值进行修正，使所创建网络的误差平方和降到最小。

本研究规定如果训练计算50 000次仍然没有收敛时，将对BP神经网络重新调整其始值的大小，而后再进行训练。

BP网络学习曲线如图 6所示，可以看出网络训练得出的误差小于1μm，达到目标值。在35 647次训练时达到目标值1.5×10-5。

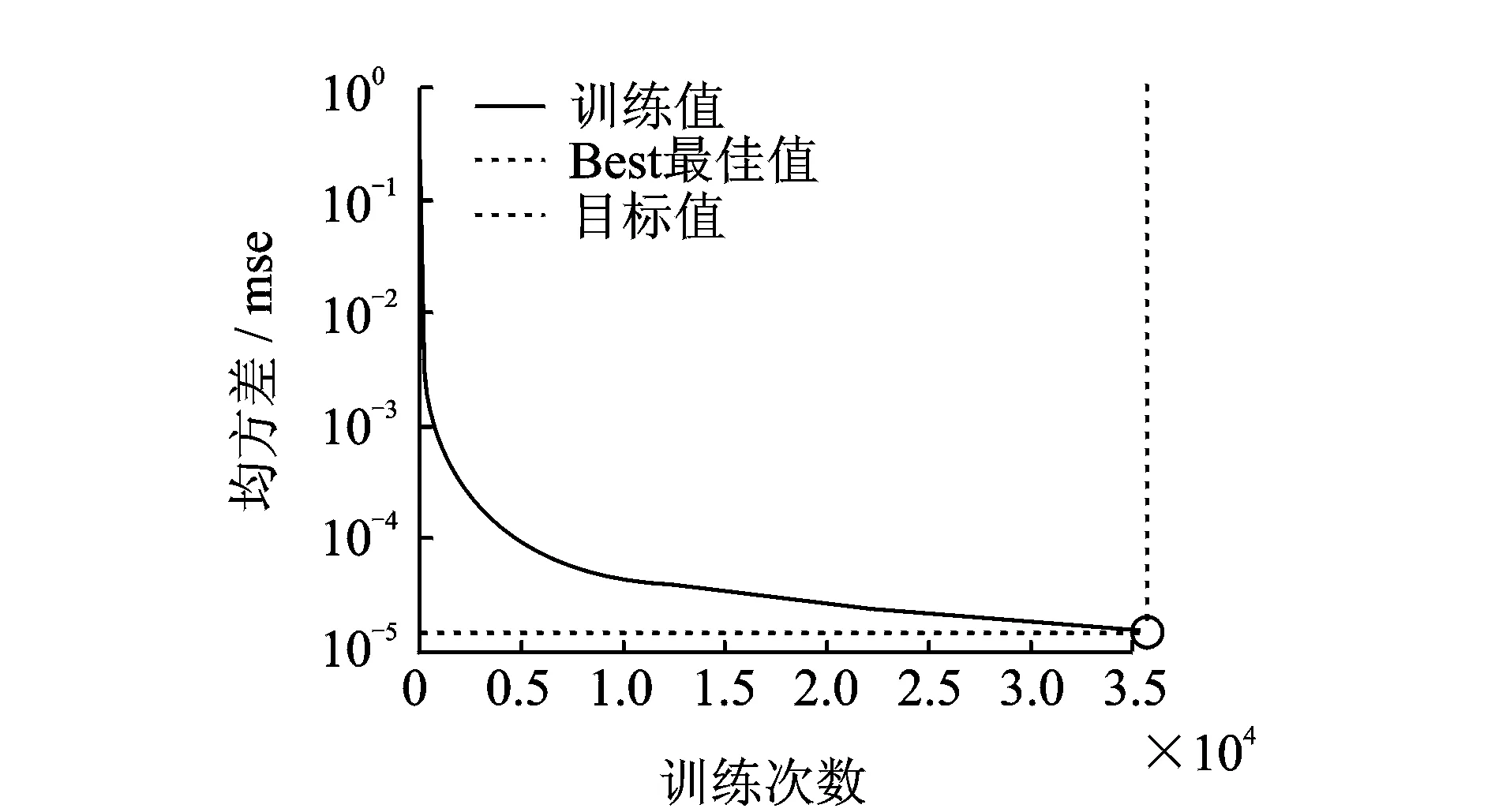
图6 BP网络学习曲线Fig.6 The learning curve of BP network

根据训练的BP网络对预测样本中的仿真数据进行预测，得到x轴和y轴定位误差的预测值。表 2列出了预测样本的仿真值和预测值。

预测样本中x轴和y轴定位误差仿真值和预测值的变化趋势如图 7所示。根据表2能够计算出平均相对预测误差为2%，说明BP网络映射模型是有效的。

表2 定位误差的仿真值和预测值

Tab.2 The simulation values and predicted values of positioning error

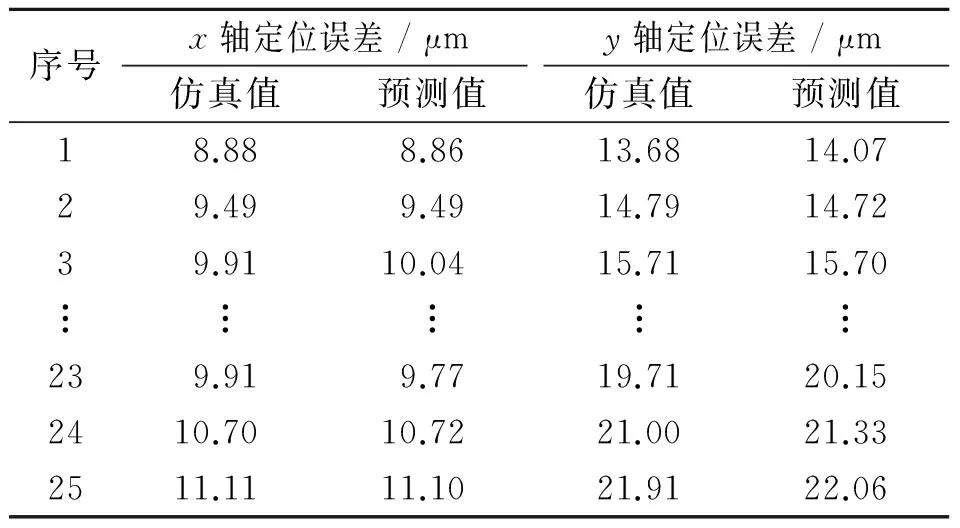
序号x轴定位误差/μmy轴定位误差/μm仿真值预测值仿真值预测值18.888.8613.6814.0729.499.4914.7914.7239.9110.0415.7115.70︙︙︙︙︙239.919.7719.7120.152410.7010.7221.0021.332511.1111.1021.9122.06

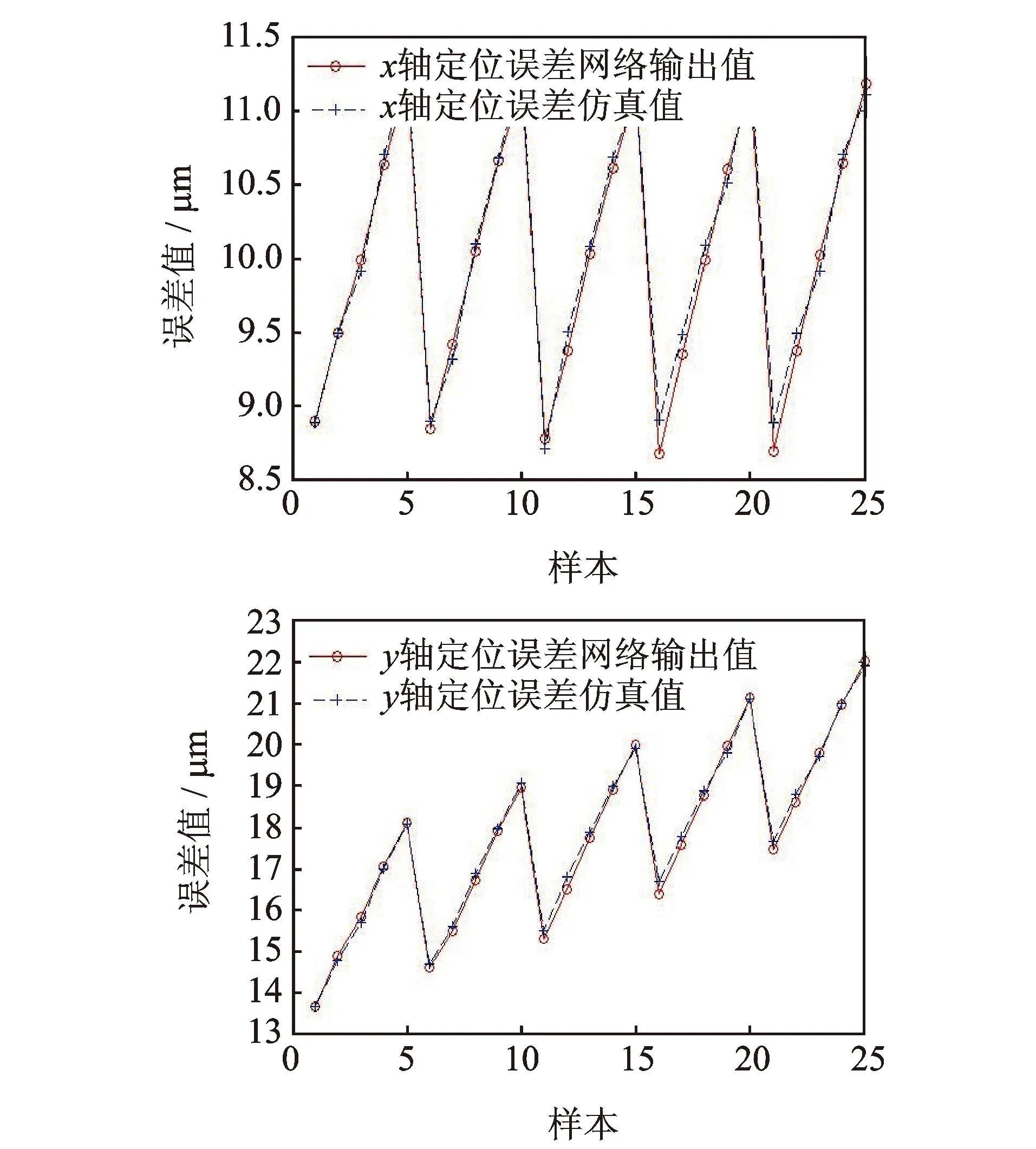
图7 定位误差仿真值和预测值变化趋势Fig.7 The trend of the simulation values and predicted values of positioning error

4 定位误差的预测

设工件负载F为定值，根据试验测得的直线度误差、反向间隙误差以及训练好的BP网络映射模型能够实现对进给伺服系统机械传动系统定位误差的预测，如图8所示。

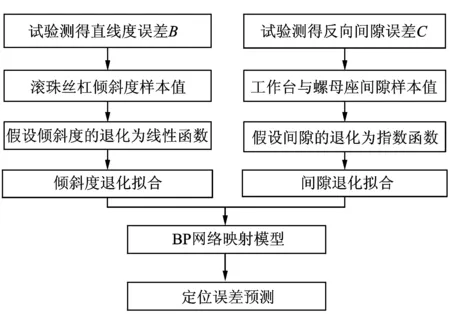
图8 基于BP网络的定位误差预测流程图Fig.8 The prediction method of positioning accuracy based on BP network

滚珠丝杠倾斜度β的拟合方法、工作台与螺母座间隙α的拟合方法及定位误差的预测方法如下。

4.1 滚珠丝杠倾斜度β的拟合

设进给伺服系统x轴滚珠丝杠倾斜度βx和y轴滚珠丝杠倾斜度βy的退化规律分别为

βx=k1t1+b1

(4)

βy=k2t2+b2

(5)

设试验测得进给伺服系统工作台运动的x轴直线度误差为Bx，y轴直线度误差为By，由前文分析βx～Bx和βy～By，通过弧度转换角度公式，计算出βx和βy的样本值。根据式(4)、式(5)，通过最小二乘法对βx，βy进行拟合。

4.2 工作台与螺母座间隙α的拟合

设进给伺服系统x轴工作台与螺母座间隙αx，y轴工作台与螺母座间隙的退化规律分别为

αx=a1+b1exp(c1t)

(6)

αy=a2+b2exp(c2t)

(7)

设试验测得进给伺服系统工作台运动的x轴反向间隙误差为Cx，y轴反向间隙误差为Cy，αx与Cx之间近似满足αx=Cx，αy与Cy之间近似满足αy=Cy，能够得到αx和αy的样本值。根据式(6)、式(7)，通过最小二乘法对αx和αy进行拟合。

4.3 基于BP网络的定位误差的预测

设定不同的工件负载F，根据拟合的αx，αy，βx及βy的退化规律以及BP网络映射模型对x轴定位误差Ax及y轴定位误差Ay进行预测，并计算相应的预测误差。预测误差最小时，工件负载F与实际最为接近，这一状态下Ax和Ay即为定位误差的预测值。

5 实例验证

5.1 试 验

根据建立的精密运动可靠性试验平台对定位误差预测方法进行验证。试验平台如图 9所示，基本设计参数如表 3所示。试验平台具有x,y两个方向的运动，采用半闭环伺服运动控制，通过光栅尺测试工作台实际位置，能动态实时获取各轴运动到设定位置时旋转编码器和光栅尺位置的差值，每隔一段时间获取并保存一组测量数据。

图9 精密运动可靠性试验平台Fig.9 The test platform of precision motion reliability

参数 参数值x方向工作行程/mm500y方向工作行程/mm300重复定位精度/μm5数据采集最小周期/ms0.5长×宽×高/mm1000×750×1000插补计时器脉冲/ms2

5.2 验 证

通过数控编程使工作台在xOy平面内运动，轨迹为450 mm×250 mm的矩形，工作台每天24 h运行，每天导出1次数据，每相隔30 d处理1次数据。根据导出的数据计算出试验台机械传动系统定位误差Ax和Ay、直线度误差Bx和By、反向间隙误差Cx和Cy。表 4列出了每相隔30d测得的试验台误差数据。

由滚珠丝杠倾斜度β的拟合方法，得到x轴滚珠丝杠倾斜度βx和y轴滚珠丝杠倾斜度βy的退化规律分别为

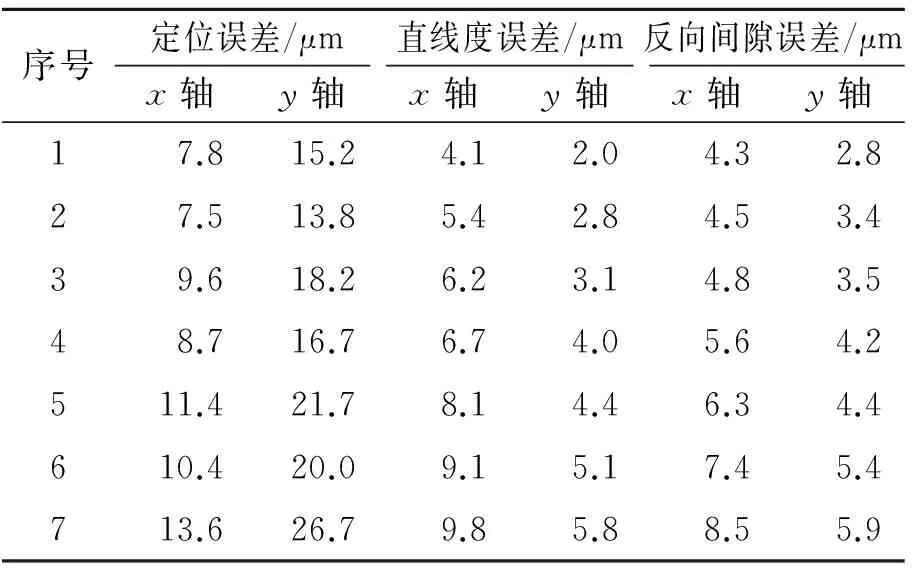
表4 精密运动可靠性试验平台试验数据

由工作台与螺母座间隙α的拟合方法，得到x轴工作台与螺母座间隙αx及y轴工作台与螺母座间隙αy的退化规律分别为

αx=(2.963 1+0.951 7exp(0.251 0t))×10-3

αy=(0.662 5+1.918 0exp(0.144 7t))×10-3

设定工件负载F，根据拟合的βx，βy，αx，αy以及BP网络映射模型对x轴、y轴定位误差Ax，Ay进行预测。经过反复验算，当扰动输入F=0.001N时，定位误差预测值和实际值最为接近。表 5列出了x轴和y轴定位误差的实际值和预测值。

表5 定位误差的实际值和预测值

Tab.1 The actual values and predicted values of positioning error

序号x轴定位误差/μmy轴定位误差/μm试验值预测值试验值预测值17.87.515.214.527.57.913.814.739.69.018.216.948.79.416.717.6511.410.621.720.4610.411.220.021.4713.612.926.725.2

根据表 5能够计算出x轴和y轴定位误差预测值和试验值的平均相对误差为6.4%，造成预测误差的原因有:a.试验的测量误差;b.BP网络本身的训练误差;c.计算误差，即通过BP网络映射模型采样以及函数参数拟合产生的误差。克服造成这3种误差的因素，可以使预测结果更为精确。与之相比较，对试验平台x轴和y轴定位误差试验数据直接进行指数函数拟合，平均相对误差为8.1%，说明笔者所提出的预测方法具有良好的预测性能。

6 结 论

1) 建立了进给伺服系统工作台与螺母座间隙、滚珠丝杠倾斜度、工件负载等与定位误差之间的BP网络映射模型。在对定位误差增长机理分析的基础上，利用所建立的BP网络映射模型对定位误差进行预测。以所建立的精密运动可靠性试验平台进行实例验证，预测值与实际值之间的误差较小，预测精度较高。通过与对定位误差试验数据直接进行指数函数拟合的对比，该方法表现出了良好的预测性能。

2) 在以后的研究中，将建立精密运动可靠性试验平台性能参数体系，进一步分析机床进给系统的多性能退化的内在规律，建立结构工艺变化与多性能之间的映射模型，这对数控装备维修决策和寿命预测技术具有重要的意义。

[1] 王胜,刘宏昭.基于神经网络的重型数控车床定位精度测量与预测[J].机械科学与技术,2011,31(4):604-608.

Wang Sheng , Liu Hongzhao. Laser measurement and prediction of position accuracy for CNC heacy-duty lathe based on netural network[J]. Mechanical and Technology for Aerospace Engineering,2011,31(4):604-608.(in Chinese)

[2] 谭雁清,张连洪,王凯峰,等.基于表面磨损的机床导轨副精度保持性模型[J].农业机械学报,2015,46(2):351-356.

Tan Yanqing , Zhang Lianhong , Wang Kaifeng,et al. Modeling of precision retaining ability for slide guide of machine tool based on wear analysis[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(2):351-356.(in Chinese)

[3] 张立新,黄玉美,乔雁龙.混联机床并联轴定位精度的激光测量与误差补偿[J].农业机械学报,2008,39(2):163-166.

Zhang Lixin , Huang Yumei , Qiao Yanlong . Laser measurement and errors compensation of position accuracy for parallel axis on hybrid NC machine tools[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008,39(2):163-166.(in Chinese)

[4] Wang Yuanhang, Deng Chao, Wu Jun, et al. Failure time prediction for mechanical device based on the degradation sequence[J]. Journal of Intelligent Manufacturing, 2013,12(5):1-19.

[5] 李斌,李曦.数控技术[M].武汉:华中科技大学出版社, 2010: 224-225.

[6] 李正守, 郭立新, 朴慧日,等. 活塞气缸拍击特性及其磨损间隙变化关系[J]. 振动、测试与诊断, 2014,34(5):838-843.

Li Zhengshou, Guo Lixin, Piao Huiri , et al. Piston slap characteristics and clearance variation of piston and cylinder[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(5):838-843.(in Chinese)

[7] 陈树越,余红英,刘广璞.BP网络算法及其在故障诊断中的应用述评[J].振动、测试与诊断,2001,21(2):100-107.

Chen Shuyue , Yu Hongying , Liu Guangpu. A review of back-propagation algorithm and its application to fault diagnosis[J].Journal of Vibration, Measurement & Diagnosis , 2001,21(2):100-107.(in Chinese)

[8] 时建峰,程珩,许征程,等. 小波包与改进BP神经网络相结合的齿轮箱故障识别[J]. 振动、测试与诊断,2009,29(3):321-324.

Shi Jianfeng, Cheng Hang, Xu Zhengcheng, et al. Fault diagnosis of gearbox using wavelet package and improved BP neural network[J].Journal of Vibration, Measurement & Diagnosis, 2009,29(3):321-324.(in Chinese)

[9] 孙春华,朱荻,李志永.基于BP神经网络的电解加工精度预测模型[J].华南理工大学学报:自然科学版,2004,32(10):24-27.

Sun Chunhua , Zhu Di , Li Zhiyong . Prediction of the workpiece accuracy during the electrochemical machini-ng based on BP neural network[J]. Journal of South China University of Technology:Natural Science Edition, 2004,32(10):24-27.(in Chinese)

[10]Dong Jingwei, Sun Meiting, Liang Gengrui, et al. The improved neural network algorithm of license plate recognition[J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2015,8(5):49-54.

[11]Ding Shifei, Su Chunyang, Yu Junzhao. An optimizing BP neural net-work algorithm based on genetic algorithm[J]. Artificial Intelligence Review, 2011, 36(2): 153-162.

[12]Cooper G R. Spinning projectile with an inviscid liquid payload impregnating porous media[J]. Amer Inst Aeronaut Astronaut Journal, 2008,46(3):783-787.

[13]韩庆楠,郝燕玲,刘志平,等.基于BP神经网络的GFSINS角速度预测[J].华中科技大学学报:自然科学版,2011,39(3):115-119.

Han Qingnan , Hao Yanling , Liu Zhiping, et al . Prediction of the angular velocity of GESINS by BP netural network[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2011,39(3):115-119.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.03.005

国家自然科学基金资助项目(51375181,51475189);国家重点研发计划政府间专项资助项目(2016YFE0121700)

2015-05-19；

2015-07-13

TH17； TP306

邓超，女，1970年5月生，教授、博士生导师。主要研究方向为质量管理与可靠性工程。曾发表《基于隐Markov模型的重型数控机床健康状态评估》 (《计算机集成制造系统-CIMS》 2013年第119卷第3期)等论文。

E-mail: dengchao@hust.edu.cn