后缘小翼智能旋翼有限偏角减振效果分析
刘士明, 杨卫东, 虞志浩, 董凌华, 陆凯华
(南京航空航天大学直升机旋翼动力学国家级重点实验室 南京,210016)
后缘小翼智能旋翼有限偏角减振效果分析
刘士明, 杨卫东, 虞志浩, 董凌华, 陆凯华
(南京航空航天大学直升机旋翼动力学国家级重点实验室 南京,210016)
建立了适合带后缘小翼的缩比模型智能旋翼减振优化分析方法。考虑小翼运动引起的气动力和惯性力对旋翼系统的影响,建立带后缘小翼的旋翼气动弹性分析模型,使用一种高效的代理模型方法计算带后缘小翼的翼型气动力。使用隐式梯形公式求解气弹耦合动力学方程得到桨叶的弹性响应,采用力积分法计算桨叶剖面振动载荷与桨毂载荷。以小翼操纵输入为设计变量,以桨毂载荷幅值为目标函数建立优化问题,使用最速下降法求解最佳减振效果对应的小翼偏转规律。结果表明本模型计算的结构与气动载荷可靠,对不同前进比状态,后缘小翼都能有效降低桨毂垂向振动载荷。使用直接约束法和目标权重法都能模拟小翼偏转能力不足的情况,小翼偏转能力对减振效果有明显影响,偏转能力不足时后缘小翼仍具有一定的减振效果。
直升机; 旋翼; 振动; 后缘小翼; 优化方法
引 言
相比固定翼飞机而言,直升机前飞时旋翼的工作环境更加复杂,振动与噪声问题严重。严格的振动标准(<0.05g)推进了直升机振动主动控制技术的发展,主动控制后缘小翼(actively controlled flap, 简称ACF)是一种重要的直升机振动主动控制方法[1]。ACF旋翼的每片桨叶外端后缘处安装一片或若干片可偏转的小翼,通过控制小翼合理地偏转,产生附加的气动力/力矩,影响旋翼的旋翼流场与气弹响应,达到降低直升机振动水平或旋翼气动噪声的目的。相比其他主动控制方法,ACF具有控制需用功率小、可靠性高等优点。
国际上比较成功的全尺寸ACF旋翼试验有SMART旋翼风洞试验[2]、Sikorsky的ACF旋翼风洞试验[3]和ADASYS智能旋翼飞行试验[4]等。与全尺寸旋翼相比,开展缩比模型旋翼试验代价相对较小,模型旋翼是验证理论计算模型和主动控制算法至关重要的工具[5]。在试验研究中ACF通常使用压电材料或磁致伸缩材料等智能材料驱动装置驱动后缘小翼[6],这些材料产生的力和位移十分有限,因而这些类型的驱动器产生的控制能力可能达不到最优减振控制的需求[7]。研究中还发现,气动力引起的铰链力矩也会明显减小后缘小翼的偏角输出[8]。对于缩比模型旋翼[9],桨叶内部空间更狭小,进行小翼驱动机构的结构设计时尤其困难,只能选用体积非常小的智能材料,此时,控制能力不足的现象会更明显。在理论研究方面,文献[10-11]分别建立了旋翼综合分析模型,通过理论研究证明主动控制后缘小翼能有效控制旋翼振动载荷;然而国际上对驱动机构控制能力不足时后缘小翼的偏转规律,以及此时后缘小翼的减振效果研究较少。进行有限偏角后缘小翼对旋翼的振动抑制分析有以下难点:高效可靠的带小翼翼型气动力计算方法;准确的后缘小翼智能旋翼气动弹性分析模型;设计变量、目标函数、优化方法的选取;模拟小翼偏转能力不足的方法。
笔者研究有限偏角的后缘小翼对智能旋翼的减振效果,建立后缘小翼智能旋翼气动弹性分析模型,并构建优化问题确定最佳减振效果对应的小翼偏转角,计算不同的前进比状态以验证方法的适用性,分析比较使用直接约束法和目标权重法两种方法在模拟小翼偏转能力不足时的减振效果。
1 智能旋翼气动弹性模型
1.1 动能与应变能
研究对象为无铰式旋翼,建模时无需考虑挥舞、摆振铰自由度,变距轴承处刚体运动θ0由操纵给定。I为惯性坐标系,H为桨毂旋转坐标系,B为桨叶变形前坐标系,E为变形后剖面坐标系。带小翼的桨叶剖面如图1所示。为描述小翼的运动,定义小翼坐标系C,C系原点位于小翼转轴处,yC正方向朝小翼前缘,xC方向同xE,zC方向由右手定则确定。
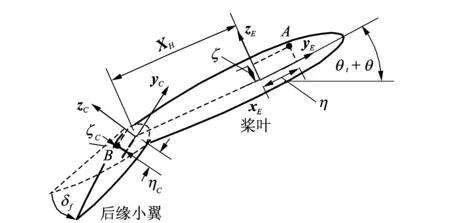
图1 剖面坐标系Fig.1 Coordinate of blade section
桨叶上质点A经刚体运动和弹性变形后,在桨毂旋转坐标系H中的坐标为
(1)

小翼的运动预先给定,不作为自由度,与桨叶上A点处于同一参考剖面上的小翼上任一点B在桨毂旋转坐标系H中的变形后坐标为
(2)
其中:(ηc,ζc)T为B点在小翼坐标系中的坐标;XH为小翼偏转轴到桨叶变距轴线的距离。
根据d′Alembert原理,以惯性力虚功的形式表示后缘小翼的动能变分
(3)
用相同方法得到桨叶的动能变分
(4)
基于几何精确的大变形梁模型推导桨叶应变能[12],考虑预扭产生的坐标系基矢量的非正交性,采用有限变形的Green应变分析桨叶应变能。桨叶应变能表达式为
δUb=∬(δεTQε)dAdx
(5)
1.2 后缘小翼旋翼气动力模型
气动力对桨叶做功由虚位移和外载荷点乘得到
(6)
其中:Gb为广义力系数矩阵;Fa和Ma为变形后坐标系中的气动力与气动力矩;qb为广义自由度;FA为气动力虚功引起的广义力。
为计算带后缘小翼的翼型气动力,笔者针对小翼偏转后剖面的实际形状划分网格,使用计算流体力学(computational fluid dynamics,简称CFD)方法计算翼型气动力,在气弹耦合过程中使用径向基函数作为CFD方法的代理模型以节约计算时间。详细计算步骤如下。
1) 对Ma,α,δf这3个变量在计算域内使用拉丁超立方法生成n个样本点。
2) 对样本点依次计算小翼绕转轴偏转δf后的翼型表面形状,翼型上点(x,y)T偏转后为
(7)
其中:(xC,yC)为小翼转轴位置。
划分小翼偏转后的翼型网格,使用CFD方法计算各样本点的二维翼型气动力,建立样本点气动力数据库。
3) 构建如下径向基函数[13]代理模型
(8)
其中:W为权重系数矩阵;φj为j点对各样本点的基函数矢量;c为正实数;r为i和j两点间欧氏距离。
由于气动力对3个变量的敏感度不同,对3个变量添加权重k1,k2,k3建立r表达式

(9)
将n个样本点的计算值代入式(10),确定权重系数矩阵
(10)
4) 对计算区间内任意未知点(Max,αx,δfx),使用代理模型计算其气动力
(11)
计算旋翼气动载荷时,桨盘平面诱导速度分布由黏性涡粒子法[14]得到,诱导速度为
(12)
其中:k为光滑参数;x为空间位置;K(ρ)为Biot-Savart核函数;α为涡粒子的涡矢量。
1.3 方程求解与载荷计算
在得到桨叶与小翼的应变能与动能变分、外力虚功后,依据Hamilton原理建立桨叶非线性动力学微分方程
(δTf+δTb-δUb+δWa)dt=0
(13)
由于高频弹性扭转及离心力的作用,旋翼动力学微分方程通常是刚性的,笔者采用隐式梯形公式与牛顿迭代算法在位形空间中求解方程[15]。使用力积分法计算桨叶结构载荷,从待求载荷的径向位置到桨尖的剖面载荷积分得到参考点处的结构载荷。由各片桨叶的桨根载荷FRk计算桨毂载荷FH
(14)
其中:Nb为桨叶片数。
带预锥角βp的旋翼,不同桨叶方位角处的坐标变换矩阵为
(15)
2 小翼操纵优化
使用2Ω~5Ω(Ω为旋翼转速)的小翼操纵用于振动控制,操纵向量δf由2Ω~5Ω小翼转角傅里叶级数这8个设计变量构成
δf=[δ2c,δ2s,δ3c,δ3s,δ4c,δ4s,δ5c,δ5s]T
(16)
一个周期内的小翼偏角表示为
(17)
对4片桨叶旋翼而言,4Ω的桨毂载荷是机身的主要振源,研究后缘小翼振动主动控制效果时,以4Ω桨毂振动的幅值建立振动目标函数Jv

(18)
研究希望最大程度地减小Jv,但是由于小翼的结构和小翼驱动机构的功率等约束,后缘小翼在工作时可能遇到偏转能力不足的情况。为模拟偏转能力不足时的小翼减振效果,介绍两种研究方法。
1) 直接约束法。直接限制小翼偏角上限δmax,在数值上对小翼偏角进行如下处理
(19)
直接约束法求解时以Jv为目标函数。
2) 目标权重法。考虑振动水平的同时,在目标函数中考虑小翼偏转角的影响。定义小翼操纵目标函数Jf为

(20)
以振动目标函数和小翼操纵目标函数加权求和的形式建立目标权重法中优化问题的最终目标函数
J=(1-wf)Jv+wfJf
(21)
其中:wf为小翼操纵目标函数权重,通过调整权重的大小能够调节偏角限制的程度。
使用最速下降法可求解优化问题,确定目标函数最小值对应的小翼操纵,步骤如下。
1) 给定第k步时小翼操纵,由有限差分法得到小翼操纵δf的目标函数梯度
Jk(δf)=(,,…,,)
(22)
2) 根据梯度的物理意义,沿梯度的反方向标量场下降最快,确定第k+1步小翼操纵的变化方向
(23)
3) 使用一维寻优法确定第k+1步的小翼操纵,要求最优步长tk满足

(24)
4) 重复步骤1~3,直到满足收敛条件‖J‖<εres时,停止迭代,εres为给定小量。
3 计算模型验证
3.1 带后缘小翼翼型气动力验证
以带0.2C后缘小翼的NACA0012翼型风洞试验结果和非定常理论计算结果[16]验证所建立的带小翼翼型气动力模型,翼型弦长C=0.18 m,Ma=0.4。基础翼型与后缘小翼的周期运动规律为

(25)
图2对升力系数和力矩系数进行了比较,可以看出本研究计算结果和文献中理论计算结果与非定常风洞试验结果吻合的都很好,证明建立的代理模型气动力计算方法可靠,可用于气动弹性计算。

图2 翼型气动力模型验证Fig.2 Validation of airfoil aerodynamic model
3.2 结构载荷验证
以全尺寸的无铰式BO105旋翼的风洞试验结果和旋翼综合分析软件CAMRAD计算结果[17]验证本旋翼模型计算结构载荷的能力。计算状态为μ=0.197,αs=-4.8°,CT/σ=0.071。从图3可以看出,本研究建立的计算模型能够很好地预测桨叶中段与根部的挥舞弯矩,总体上精度优于使用自由尾迹/准定常气动模型计算的CAMRAD/JA。0.144R处于150°方位角附近的挥舞弯矩预测结果比CAMRAD/JA更接近试验值(见图3(a)),很好地捕捉到了0.57R处旋翼后行边挥舞弯矩的变化情况(见图3(b))。
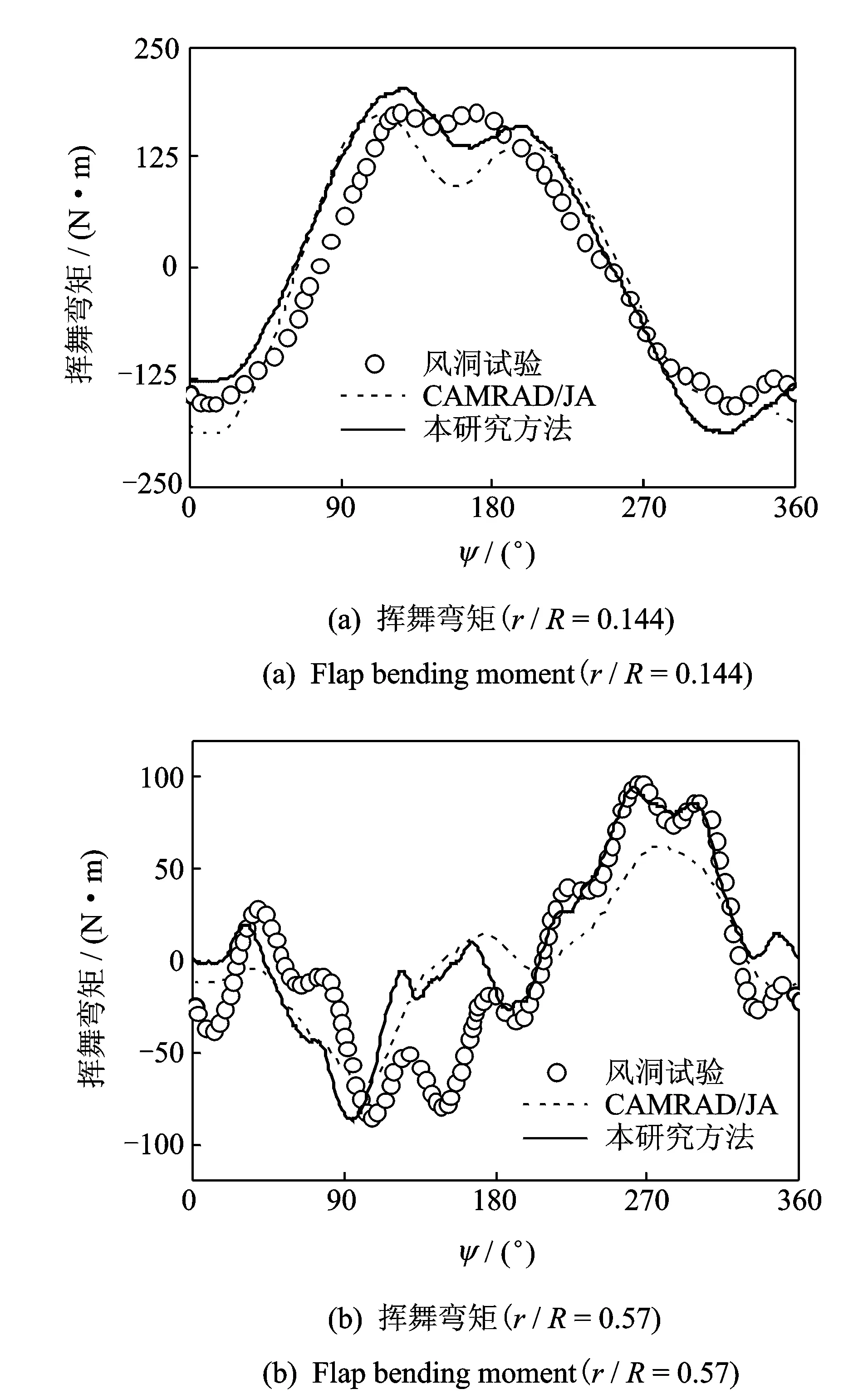
图3 旋翼载荷验证Fig.3 Validation of rotor load
3.3 气动载荷验证
SMART旋翼试验是目前最成功的带小翼全尺寸旋翼风洞试验,文献[18]使用两种方法对该旋翼进行了分析,即Freewake/ UMARC耦合计算方法和CFD/ UMARC耦合计算方法,计算文献[18]的case2状态。考虑到小翼偏转对剖面气动力矩的影响比对升力系数和阻力系数的影响更显著,俯仰力矩更难预估,比较小翼内端0.74R与小翼中部0.82R两个剖面处的俯仰力矩,验证本方法计算带小翼旋翼气动载荷的能力。从图4可以看出,3种计算方法得到的俯仰力矩系数结果接近,证明了笔者建立的气动模型的准确性,可用于带后缘小翼的旋翼载荷计算。
4 数值计算与讨论
研究半径为1.143 m的4片桨叶的模型旋翼,其弦长为0.086 m,无尖削,无预扭,工作转速为760 r/min,翼型为NACA0012,桨叶结构参数见表1,其中1号段为柔性段,4号段为小翼段。小翼尺寸及位置见图5。
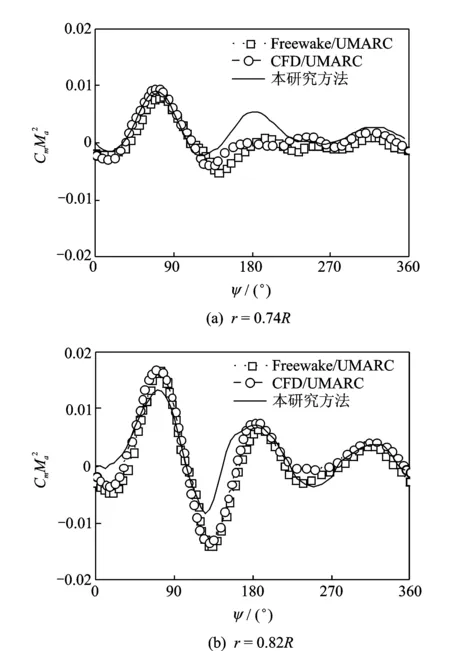
图4 带后缘小翼桨叶剖面俯仰力矩比较Fig.4 Pitch moment of blade section with ACF

图5 后缘小翼位置与尺寸Fig.5 Position and dimension of ACF
4.1 自由小翼减振分析
对小翼的偏角幅值不做任何约束,小翼操纵目标函数权重wf取0,计算4个前进比状态(μ=0.1,
0.15, 0.2, 0.25),拉力系数为0.005,旋翼轴前倾角为0°,配平使桨根1阶挥舞弯矩分量为0,忽略小翼偏转对旋翼配平的影响。
图6对不同前进比状态的小翼静止及小翼受控优化时的4Ω桨毂垂向载荷进行了比较,可以看出,前进比越大,小翼静止时的垂向桨毂振动载荷越大。对于不同的前飞速度,通过优化小翼控制的方法都能有效降低4Ω桨毂垂向载荷。
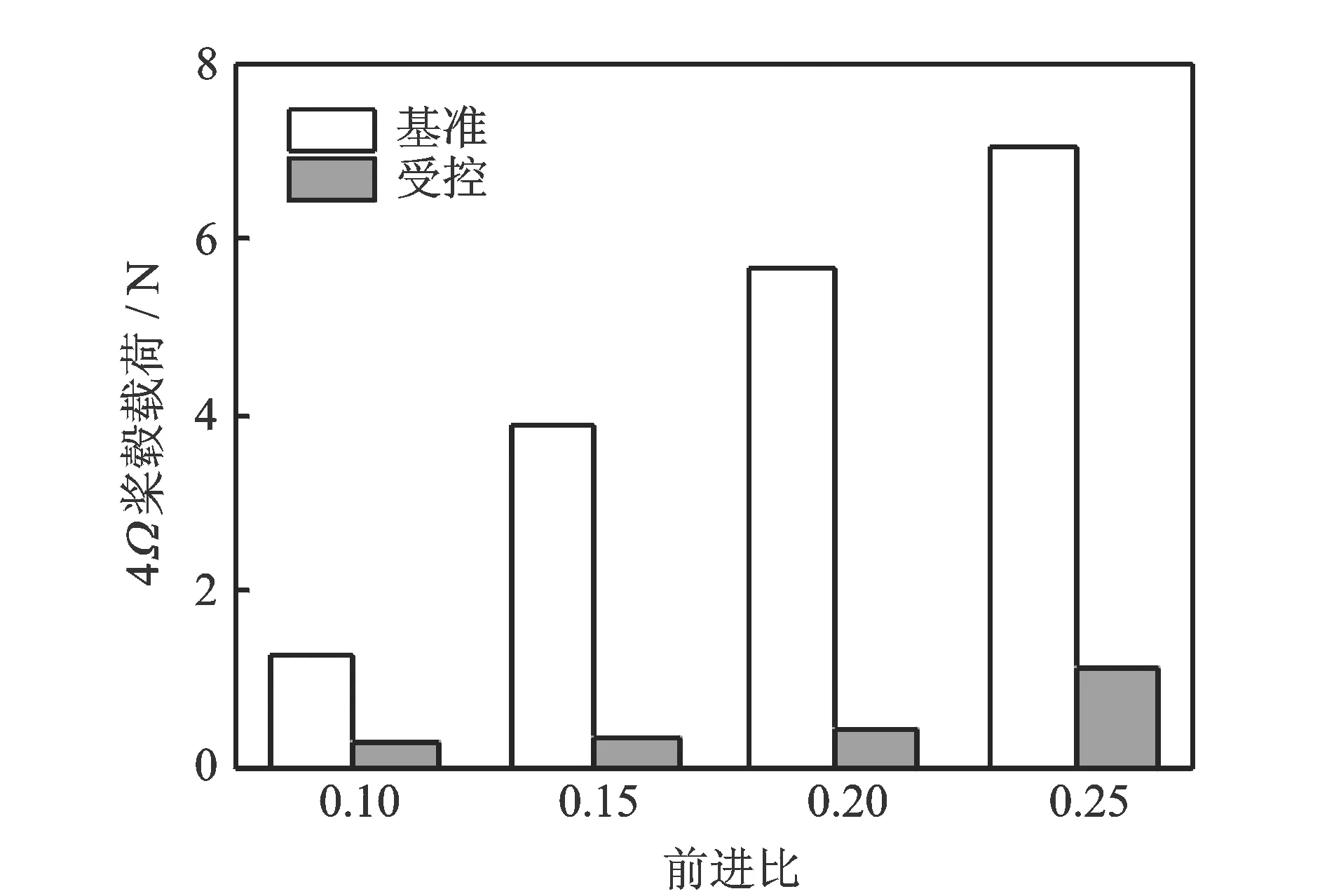
图6 4 Ω桨毂垂向载荷控制效果Fig.6 Control effect of 4 Ω vertical hub load
前进比越大,桨毂振动载荷越大,需要小翼产生更大的气动力用于抑制振动载荷,因此减振需要的小翼偏转幅值越大。不同前进比状态优化得到的小翼偏转规律如图7所示。几个计算状态的小翼在旋翼前行边的偏转幅度普遍大于后行边的偏转幅度,且前行边的偏转规律在相位上具有相似性。
对μ=0.2状态,振动目标函数Jv由6.31降至2.74,下降了56.6%。图8对此前进比小翼受控前后的桨根处垂向剪力和扭转力矩的谐波幅值进行了比较。本研究计算非均匀诱导速度分布时使用的黏性涡粒子法能够捕捉到气动载荷的高阶成分,桨叶在高阶的气动载荷作用下于根部形成高阶的结构载荷。垂向剪切力中的3,4,5阶谐波传到桨毂上,形成4Ω的垂向桨毂振动载荷,这是垂向桨毂振动的主要来源。从图8(b)可见,扭转力矩谐波中1阶幅值最明显,这是前飞状态周期变距操纵产生的。小翼不工作时除1阶以外其他阶次的幅值均非常小,小翼向下偏转时改变了原有翼型的弯度,在翼型后缘下表面形成明显的高压区,将显著改变翼型的俯仰力矩系数,由于2Ω~5Ω的小翼运动,明显增加了2~5阶扭转弯矩幅值。

表1 模型旋翼结构参数

图7 不同前进比小翼控制规律Fig.7 ACF control law of different advance ratio

图8 桨根载荷谐波幅值(μ=0.2) Fig.8 Amplitude of load harmonics at blade root(μ=0.2)
通过优化小翼偏转规律,桨根垂向力的4阶谐波基本降为0,其他阶次的幅值和相位也都有所变化,合成后的垂向桨毂振动载荷明显降低,如图9所示。小翼偏转输入仅包含2Ω~5Ω,对更高阶的振动影响不明显。从图9可以看出,减振后的垂向桨毂力仍保留明显的8阶成分。

图9 垂向桨毂振动载荷(μ=0.2)Fig.9 Vertical vibratory hub load(μ=0.2)
4.2 直接约束法
设计的模型旋翼后缘小翼驱动机构使用3个串联的PTJ200系列压电堆驱动菱形框带动小翼偏转,使用ANSYS分析驱动机构在交变的额定电压(200 V)作用下的工作能力。计算得到不同频率电压作用下的小翼偏转能力如表2所示,无气动力作用时设计的驱动机构在小翼工作频率附近的偏转能力约为±3°,实际工作时由于气动力的作用,偏转幅值会更小。
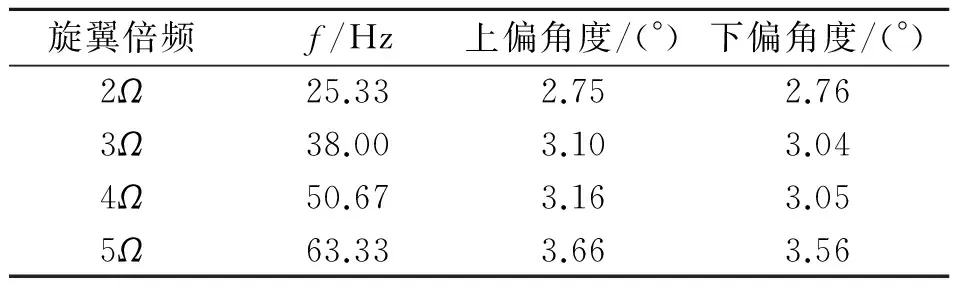
表2 小翼偏角幅值
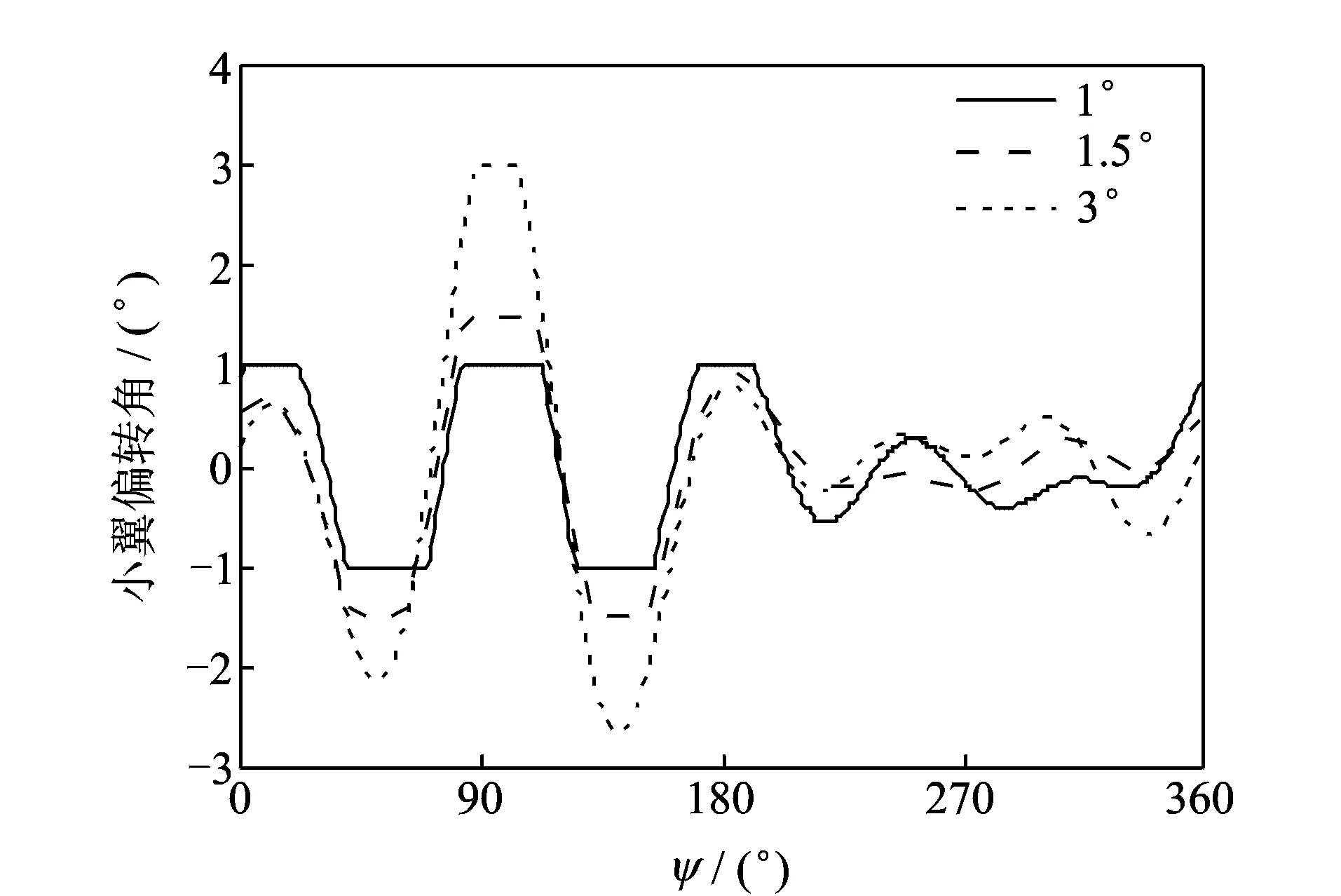
图10 直接约束法小翼偏转角Fig.10 Deflection angle with direct constraint method
针对设计的小翼驱动机构驱动能力,使用直接约束法(wf=0)分析有限偏角小翼的减振效果,分别对δmax=1°,1.5°,3°这3种情况进行分析,计算得到的最优小翼偏转角如图10所示。可以看出,不同的偏角上限对小翼控制律的相位影响较小,对幅值影响较大。±3°的限制几乎没有影响到小翼的自由偏转,此时4Ω桨毂垂向振动载荷降低了92.4%,减振效果十分明显。当小翼仅在±1°的范围内偏转时,最优状态能降低71.2%的4Ω桨毂垂向振动载荷。
比较图11中不同方向的桨毂载荷可以发现,后缘小翼智能旋翼对垂向桨毂振动载荷影响最明显,由于各自由度之间的耦合作用,垂向桨毂振动降低的同时其他方向的载荷也有所变化。虽然小翼运动使桨根扭转振动载荷大幅增加,如图8(b)所示,但是其数值与桨根挥舞弯矩相比太小,所以在合成为桨毂俯仰和滚转力矩后体现不出扭转力矩的影响。

图11 直接约束法4Ω桨毂载荷Fig.11 4Ω hub load with direct constraint method

图12 目标权重法小翼偏转角Fig.12 Deflection angle with objective weight method
4.3 目标权重法
目标权重法通过加权的形式重构目标函数,图12对不同权重系数得到的优化小翼偏角进行了比较。可以看出,适当增加权重系数wf能有效降低小翼偏角的峰-峰值,模拟小翼受驱动机构、小翼铰链力矩等限制导致的偏转能力不足的情况,但不同权重系数得到的小翼偏转相位基本相同。当wf=0.05时,小翼偏角峰-峰值为4.16°,此时4Ω垂向桨毂振动载荷降低了47.8%,如图13所示。

图13 目标权重法4Ω桨毂载荷Fig.13 4Ω hub load with objective weight method
4.4 偏角限制方法比较
前两节结果显示,直接约束法与目标权重法都能在减振的同时约束小翼的偏角峰值。图14比较了两种方法,由图可见:直接约束法的目标函数Jv随δmax的降低先平缓变化后剧烈增加,δmax>2°时减振效果都比较好;目标权重法的Jv始终随δmax的降低而明显增加,呈单调关系。整体上,对于相同的δmax使用直接约束法得到的Jv更小,对小翼偏角做过多的约束会明显影响小翼的减振效果。

图14 偏角约束方法比较Fig.14 Comparison of flap angle constraint methods
5 结 论
1) 笔者建立的模型能准确计算旋翼结构载荷与前飞时带后缘小翼的旋翼气动载荷。
2) 前进比越大,桨毂垂向载荷的幅值越大。基于优化方法的后缘小翼减振分析模型有效,可确定不同前进比最佳减振状态的小翼偏角规律。
3) 使用直接约束法或目标权重法能够模拟小翼偏转能力不足的情况。偏转能力对减振效果有明显影响,为保证减振效果,工程中应尽量增强驱动机构的能力。
[1] Friedmann P P. On-blade control of rotor vibration, noise, and performance: just around the corner? [J]. Journal of the American Helicopter Society, 2014, 59(4): 1-37.
[2] Hagerty B, Kottapalli S. Boeing SMART rotor full-scale wind tunnel test data report [R]. California: NASA Ames Research Center, 2012.[3] Sim B, Potsdam M, Kitaplioglu C, et al. Localized, non-harmonic active flap motions for low frequency in-plane rotor noise reduction [C] ∥AHS 68th Annual Forum. Fort Worth, TX: AHS International, 2012: 8-23.
[4] Lorber P, Hain B, Wang J, et al. Rotor aeromechanics results from the Sikorsky active flap demonstration rotor [C] ∥ AHS 68th Annual Forum. Fort Worth, TX: AHS International, 2012: 553-568.
[5] Koratkar N A, Chopra I. Open-loop hover testing of a smart rotor model [J]. AIAA Journal, 2002, 40(2): 1495-1502.
[6] Lee J H, Natarajan B, Eun W J, et al. Structure and mechanism design of an active trailing-edge flap blade [J]. Journal of Mechanical Science and Technology, 2013, 27(9): 2605-2617.
[7] Cribbs R, Friedmann P P. Actuator saturation and its influence on vibration reduction by actively controlled flaps [C] ∥AIAA/SME/ASCE/AHS/ ASC Structures, Structural Dynamics and Materials Conference. Stratford, CT: AIAA Inc, 2001: 2101-2111.
[8] 张柱, 黄文俊, 杨卫东. 后缘小翼型智能旋翼桨叶模型设计分析与试验研究 [J]. 南京航空航天大学学报, 2011, 43(3): 296-301.
Zhang Zhu, Hhuang Wenjun, Yang Weidong. Design analysis and test of smart rotor blades model with trailing edge flaps [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(3): 296-301.(in Chinese)[9] Fulton M V, Orimiston R A. Hover testing of a small-scale rotor with on-blade elevons [J]. Journal of the American Helicopter Society, 2001, 46(2): 96-106.
[10]Patt D, Liu L, Friedmann P P. Rotorcraft vibration reduction and noise prediction using a unified aeroelastic response simulation [J]. Journal of the American Helicopter Society, 2005, 50(1):95-106.
[11]Falls J, Datta A, Chopra I. Integrated trailing-edge flaps and servotabs for helicopter primary control [J]. Journal of the American Helicopter Society, 2010, 55(3): 1-15.
[12]虞志浩, 杨卫东, 张呈林. 基于Broyden法的旋翼多体系统气动弹性分析 [J]. 航空学报, 2012, 33(12): 2171-2182.
Yu Zhihao, Yang Weidong, Zhang Chenglin. Aeroelasticity analysis of rotor multibody system based on Broyden method [J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2171-2182.(in Chinese)
[13]穆雪峰, 姚卫星, 余雄庆, 等. 多学科设计优化中常用代理模型的研究 [J]. 计算力学学报,2005,22(5): 608-612.
Mu Xuefeng, Yao Weixing, Yu Xiongqing, et al. A survey of surrogate models used in MDO [J]. Chinese Journal of Computational Mechanics, 2005, 22(5): 608-612.(in Chinese)
[14]谭剑锋, 王浩文, 吴超, 等. 基于非定常面元/黏性涡粒子混合法的旋翼/平尾非定常气动干扰 [J]. 航空学报,2014,35(3): 643-656.
Tan Jianfeng, Wang Haowen, Wu Chao, et al. Rotor/empennage unsteady aerodynamic interaction with unsteady panel/viscous vortex particle hybrid method [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 643-656.(in Chinese)
[15]吴杰, 杨卫东, 虞志浩. 旋翼桨叶结构载荷计算方法比较研究 [J]. 振动与冲击, 2014, 33(7): 210-214.
Wu Jie, Yang Weidong, Yu Zhihao. Comparison among rotor blade structural load calculation methods [J]. Journal of Vibration and Shock, 2014, 33(7): 210-214.(in Chinese)
[16]Krzysiak A, Narkiewicz J. Aerodynamic loads on airfoil with trailing-edge flap pitching with different frequencies [J]. Journal of Aircraft, 2006, 43(2): 407-418.
[17]Peterson R L, Maier T. Correlation of wind tunnel and flight test results of a full-scale hingeless rotor [C] ∥AHS Aeromechanics Specialists Conference. Washington DC: AHS International, 1994.
[18]Ananthan S, Baeder J, Sim B W, et al. Prediction and validation of the aerodynamics, structure dynamics, and acoustics of the SMART rotor using a loosely-coupled CFD-CSD analysis [C] ∥ AHS 66th Annual Forum. Phoenix, AZ: AHS International, 2010: 2031-2057.

10.16450/j.cnki.issn.1004-6801.2017.03.003
国家自然科学基金资助项目(11272148);重点实验室基金资助项目(9140C400401140C40183);江苏高校优势学科建设工程资助项目
2015-12-11;
2016-02-25
TH113; V211.47
刘士明,男,1991年1月生,博士。主要研究方向为直升机旋翼动力学。曾发表《优化转速旋翼性能分析与应用》(《南京航空航天大学学报》2014年第46卷第6期)等论文。
E-mail: liushiming@nuaa.edu.cn

