基于EEMD的行星齿轮箱齿轮裂纹损伤定位

刘浩华， 李方义， 李国彦， 王一凡， 张珊珊， 董德浩

(1.山东大学高效洁净机械制造教育部重点实验室 济南，250061)(2.上海航天设备制造总厂 上海，200245)



基于EEMD的行星齿轮箱齿轮裂纹损伤定位

刘浩华1， 李方义1， 李国彦1， 王一凡2， 张珊珊1， 董德浩1

(1.山东大学高效洁净机械制造教育部重点实验室 济南，250061)(2.上海航天设备制造总厂 上海，200245)

针对行星齿轮式变速箱的齿轮裂纹损伤难以提取特征频率和定位的问题，提出基于总体平均经验模式分解(ensemble empirical mode decomposition，简称EEMD)的齿轮局部损伤频率解调分析方法。该方法在建立的齿轮局部损伤振动信号模型的基础上，分别对太阳轮、齿圈、行星轮的裂纹损伤信号进行EEMD分解和频率解调分析，通过频谱图提取齿轮的局部损伤特征频率，从而识别变速箱中裂纹损伤齿轮的位置。综合仿真分析和试验结果表明，基于EEMD的齿轮局部损伤频率解调分析方法可以有效地提取太阳轮、齿圈和行星轮的裂纹损伤特征频率，实现行星齿轮式变速箱中齿轮裂纹损伤的定位。

变速箱； 频率解调； 损伤定位； 总体平均经验模式分解

引 言

行星齿轮式变速箱因其结构紧凑、传动平稳、承载能力强，被广泛应用在工程机械、航空航天及船舶车辆等的传动系统当中，因此，对其进行振动检测的意义重大[1]。但是由于采集到的变速箱振动信号包含齿轮、行星架及轴承等各部件的信息成分，加上隐含的噪声干扰，振动信号的非平稳、复杂性和非线性特征十分明显，传统的信号处理方法难以提取和识别微弱的损伤故障特征信息[2-4]。

近年来，EEMD方法广泛应用于故障诊断领域。Rajeswari等[5]用EEMD和混合二进制蝙蝠算法相结合的方法提取不同齿轮损伤的特征频率。Žvokelj等[6]综合EEMD和多尺度独立分量分析方法的优点，检测轴承的早期损伤。孙曙光等[7]将EEMD与小波阈值结合，有效消除了噪声对信号的干扰。陈虹屹等[8]将EEMD与奇异熵分析相结合，提取高速道岔振动信号中的裂纹损伤特征信息。本研究针对特殊的行星齿轮式变速箱复杂结构，建立相应的振动信号模型，提出基于EEMD的齿轮局部损伤频率解调分析方法，并通过仿真分析和试验研究，提取太阳轮、齿圈和行星轮裂纹损伤的特征频率，验证该方法的有效性。

1 行星齿轮式变速箱齿轮局部损伤振动信号模型

因本研究所用的行星齿轮式变速箱的齿圈是浮动的，振动信号不易通过齿圈传递到箱体，故不考虑行星架的旋转效应。结合齿轮振动理论和行星齿轮式变速箱特殊结构，借鉴Feng等[9]对齿轮箱振动信号模型的研究，建立了行星齿轮式变速箱的齿轮局部损伤振动信号模型

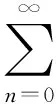
(1)

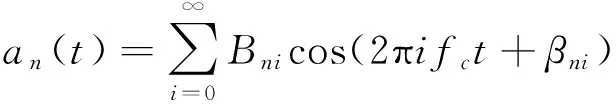
(2)

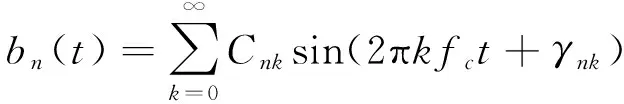
(3)

其中：A为信号的振幅，是常数；fmesh为啮合频率；an(t)为幅值调制函数；bn(t)为频率调制函数；Bni为调幅函数的n次谐波的调制强度；Cnk为调频函数的n次谐波的调制强度；fc为齿轮的局部损伤特征频率；αn，βni，γnk为初始相位。

对于式(2)，当i=0时，Bn0=1，βn0=0。

由于式(1)～式(3)中的基频不仅具备齿轮局部损伤振动信号模型的代表性，而且在振动的谐波成分中，基频一般会具有最大的振幅。所以在只考虑基频[9]而不考虑其高次谐波的情况下，可将行星齿轮式变速箱齿轮局部损伤振动信号模型简化为

y(t)=A[1+Bcos(2πfct+β)]cos[2πfmesht+

Csin(2πfct+γ)+α]

(4)

其中：B，C分别为调幅函数和调频函数的基频的调制强度；α，β，γ为基频的初始相位。

2 基于EEMD的齿轮局部损伤频率解调分析

针对第1节所建立的齿轮局部损伤振动信号模型的特点，本节提出了基于EEMD的齿轮局部损伤频率解调分析方法。首先，介绍了振动信号频率解调分析方法的优点；其次，借助EEMD来改善频率解调分析方法存在的问题；最后，总结了基于EEMD的频率解调分析方法的诊断步骤。

2.1 振动信号的频率解调分析

由式(4)可知，单独来看振动信号模型的调频成分，它包含齿轮局部损伤引起的特征频率fc，而且频率成分简单易懂，不受调幅部分的调制频率的影响，避免了传统傅里叶频谱中边带成分复杂而难以辨别的不足[10]。所以研究调频部分的频谱结构，能更加简便有效地提取齿轮局部损伤的特征频率。

式(4)中调频部分的瞬时相位可表示为

φ(t)=2πfmesht+Csin(2πfct+γ)+α

(5)

其中：各项参数的含义与式(4)相同。

将瞬时相位在时间上进行微分计算，即可得到相应的瞬时频率

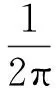
(6)

对式(6)进行傅里叶变换，可以得到瞬时频率的傅里叶频谱

F(f)=fmeshδ(f)+Cfcδ(f-fc)exp(jγ)

(7)

如式(6)所示，因为啮合频率fmesh是固定不变的常量，并且与齿轮的局部损伤无关，所以通过观察瞬时频率的波动成分，即可提取齿轮局部损伤的特征信息。又如式(7)所示，齿轮的局部损伤特征频率fc与瞬时频率的波动周期相关，若转化到瞬时频率的傅里叶频谱图中，则局部损伤特征频率fc的位置将会出现峰值。若综合考虑齿轮局部损伤特征频率的高次谐波对于振动信号频率调制作用的影响，则转化到瞬时频率的傅里叶频谱图中，局部损伤特征频率的倍频nfc的位置也会出现峰值。因此，在瞬时频率的傅里叶频谱中，只需找到峰值处的频率之间的关系，便可直观地提取出齿轮局部损伤特征频率fc及其倍频nfc，从而识别行星齿轮式变速箱中齿轮局部损伤的位置。

频率解调分析仅适合处理频率成分简单的单分量信号，但实际采集到的行星齿轮式变速箱振动信号一般为非平稳、多分量的复杂信号，所以必须先将采集的原始信号分解为单分量信号。

2.2 总体平均经验模式分解EEMD

经验模式分解(empirical mode decomposition，简称EMD)是一种具有自适应优势的新的信号处理方法，可以按照信号的局部特性实现相应的时频分解。其理论重点是提出了固有模式函数(intrinsic mode functions，简称IMF)的概念，但是EMD方法在实际应用中会出现模式混叠的问题[11]。

EEMD是在EMD方法的基础上提出的。它结合高斯白噪声具备的频率均匀分布的统计优点，在原始信号中加入白噪声，促使信号在不同时间尺度上拥有连续性，从而改善模式混叠现象的程度。按照EEMD的算法步骤[12]，可将原始信号y(t)分解为

y(t)=∑jcj(t)+rn

(8)

其中：cj(t)为EEMD分解后得到的第j个IMF分量；rn为最终的残余量，一般为平稳的单调函数或常量，表示信号的基本趋势走向。

EEMD方法可以把任意复杂的多分量原始信号y(t)分解成若干个单分量的IMF成分和一个残余量。其中单分量的IMF信号按照分解的先后顺序，表示信号不同频段的成分由高到低排列，即每个IMF分量信号包含不同的频率和带宽成分，而且会随着y(t)的变化而自适应性地变化。

2.3 基于EEMD的频率解调分析诊断步骤

1) 应用EEMD方法将复杂的原始信号分解为单分量的IMF成分。

2) 先借助式(9)对IMF分量信号c(t)进行Hilbert变换，然后借助式(10)～式(11)求得每个IMF分量的瞬时频率[10]

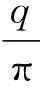
(9)

其中：h(t)由IMF分量c(t)经过Hilbert变换得到；q为Cauchy主值。

瞬时相位φ(t)可表示为

φ(t)=arctan[h(t)/c(t)]

(10)

瞬时频率f(t)可表示为

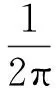
(11)

3) 选取EEMD分解出的前4个IMF分量信号的瞬时频率，并求其平均值。原因如下：a.EEMD分解出的IMF分量按照频段由高到低的顺序排列；b.齿轮损伤产生的冲击特征在高频段更为敏感和明显，一般蕴含在前面几个高频段的IMF分量中，所以本研究主要选取了前4个IMF分量进行计算[12]；c.EEMD方法具有完备性，即原始信号的性质可以通过将各IMF分量相加的方式来体现[13]，所以求前4个IMF分量的瞬时频率的均值，是为了尽可能保证高频段信号中的齿轮损伤特征信息的完备性，同时消除低频段的一些干扰噪声。

4) 对前4个IMF分量的瞬时频率均值进行傅里叶变换，然后在瞬时频率的傅里叶频谱中，根据峰值处的频率，提取出齿轮局部损伤特征频率fc及其倍频nfc，从而识别齿轮局部损伤的位置。

3 仿真分析验证

为验证本研究提出的基于EEMD的频率解调分析方法的准确性，需要利用仿真信号处理分析。假设太阳轮产生了局部损伤，按照式(4)表示的振动信号模型，生成如下仿真信号

y(t)=[1+cos(2π18t)]cos[2π181t+sin(2π18t)]

(12)

仿真信号的参数如表1所示，其中太阳轮的局部损伤特征频率fs设为18 Hz。考虑到实际振动信号中的噪声成分，在仿真信号中添加了方差为0.5、均值为1的高斯白噪声。仿真信号的时域图如图1所示，可观察到明显的幅值调制和频率调制成分，证明了前面所建立的振动信号模型的合理性。

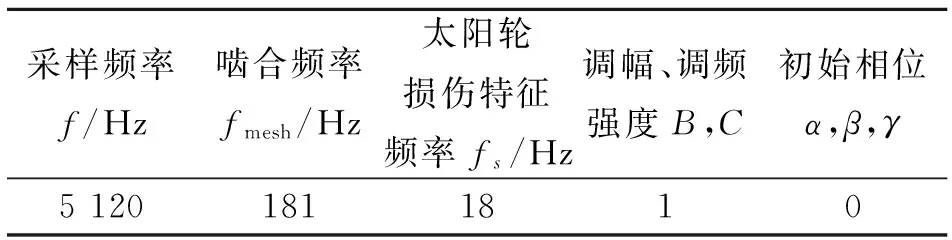
表1 仿真信号参数设置

图2为原始信号y(t)经EEMD方法分解而得到的各IMF分量的时域图，对比IMF1～IMF12分量的时域图，发现信号的频率依次减小，齿轮损伤产生的冲击特征在高频段的IMF分量中更加明显。分别计算前4个IMF信号的瞬时频率并求其平均值，最后对瞬时频率的平均值进行傅里叶变换，得到图3。在图3所示的瞬时频率傅里叶频谱图(其纵坐标仅具有相对意义)中，峰值频率出现在横坐标的18，36，54，72 Hz等处，即太阳轮的局部损伤特征频率fs及其倍频nfs处，而且fs处的峰值最明显，符合理论预期效果。可以判定太阳轮产生了局部损伤，从而验证了基于EEMD的频率解调分析方法的准确性，而且瞬时频率傅里叶频谱图更加简单直观，更易有效地提取齿轮局部损伤的特征频率。

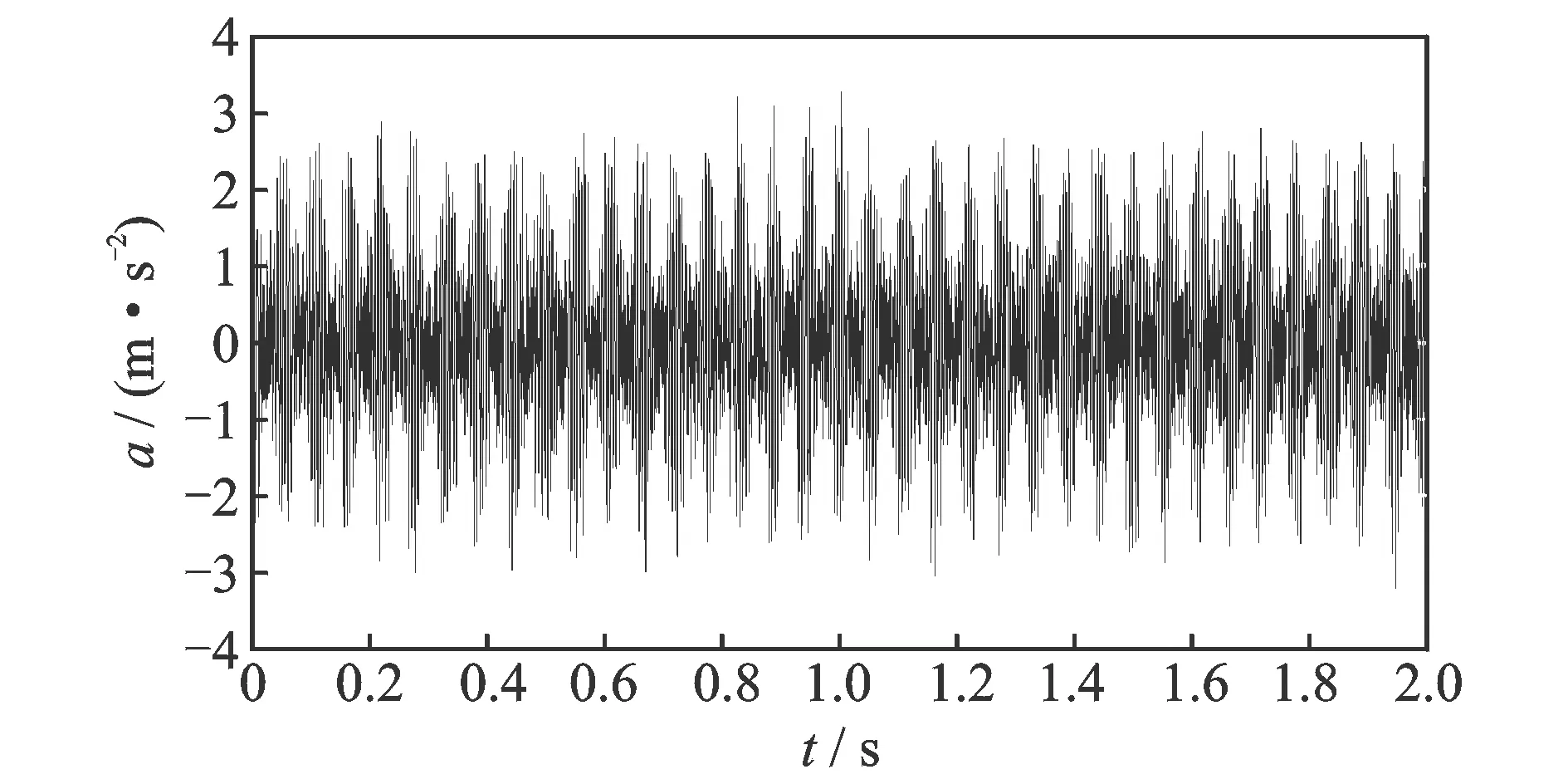
图1 仿真信号的时域图Fig.1 Time-domain plot of the simulation signal

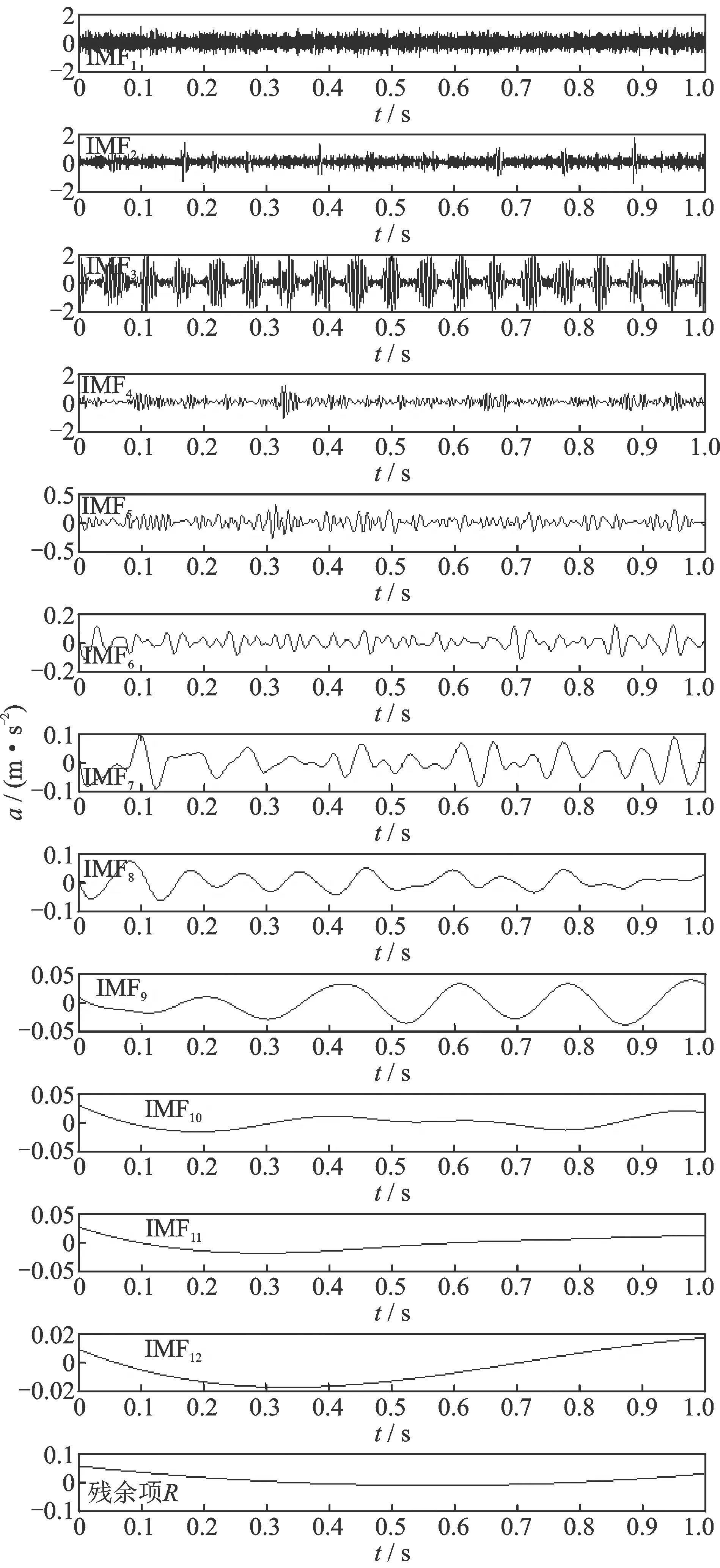
图2 EEMD分解得到的各IMF分量时域图Fig.2 Time-domain plot of IMFs decomposed by EEMD

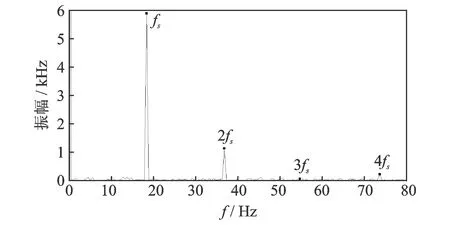
图3 瞬时频率的傅里叶频谱图Fig.3 Fourier spectrum of the instantaneous frequency

4 行星齿轮式变速箱齿轮裂纹损伤定位实例分析

4.1 试验说明

根据试验台架的性能参数，变速箱的输入转速设置为700 r/min，负载设置为200 N·m，采样频率设置为5 120 Hz，把采集振动信号的加速度传感器置于变速箱输入端轴承盖的上方。以线切割方式分别加工宽为0.4 mm、深为5 mm的太阳轮、齿圈和行星轮齿根裂纹，其中行星齿轮式变速箱结构及3种齿轮的裂纹损伤形式如图4所示。最后，根据行星齿轮式变速箱的结构参数，由式(13)～式(16)计算得到第2级行星齿轮系的啮合频率与各齿轮局部损伤的特征频率[14]，如表2所示。

fmesh=fcarrierZr

(13)

fs=(fmesh/Zs)N

(14)

fr=(fmesh/Zr)N

(15)

fp=fmesh/Zp

(16)

其中：fmesh为啮合频率；fcarrier为旋转的行星架的频率；fs，fr，fp分别为太阳轮、齿圈、行星轮的局部损伤特征频率；Zs，Zr，Zp分别为太阳轮、齿圈、行星轮的齿数；N为行星轮的个数。

图4 试验说明Fig.4 Test introduction

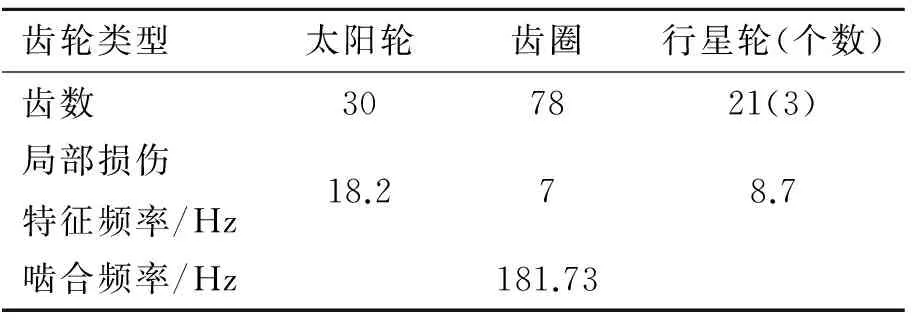
齿轮类型太阳轮齿圈行星轮(个数)齿数307821(3)局部损伤特征频率/Hz18.278.7啮合频率/Hz181.73

4.2 太阳轮裂纹损伤定位实例分析

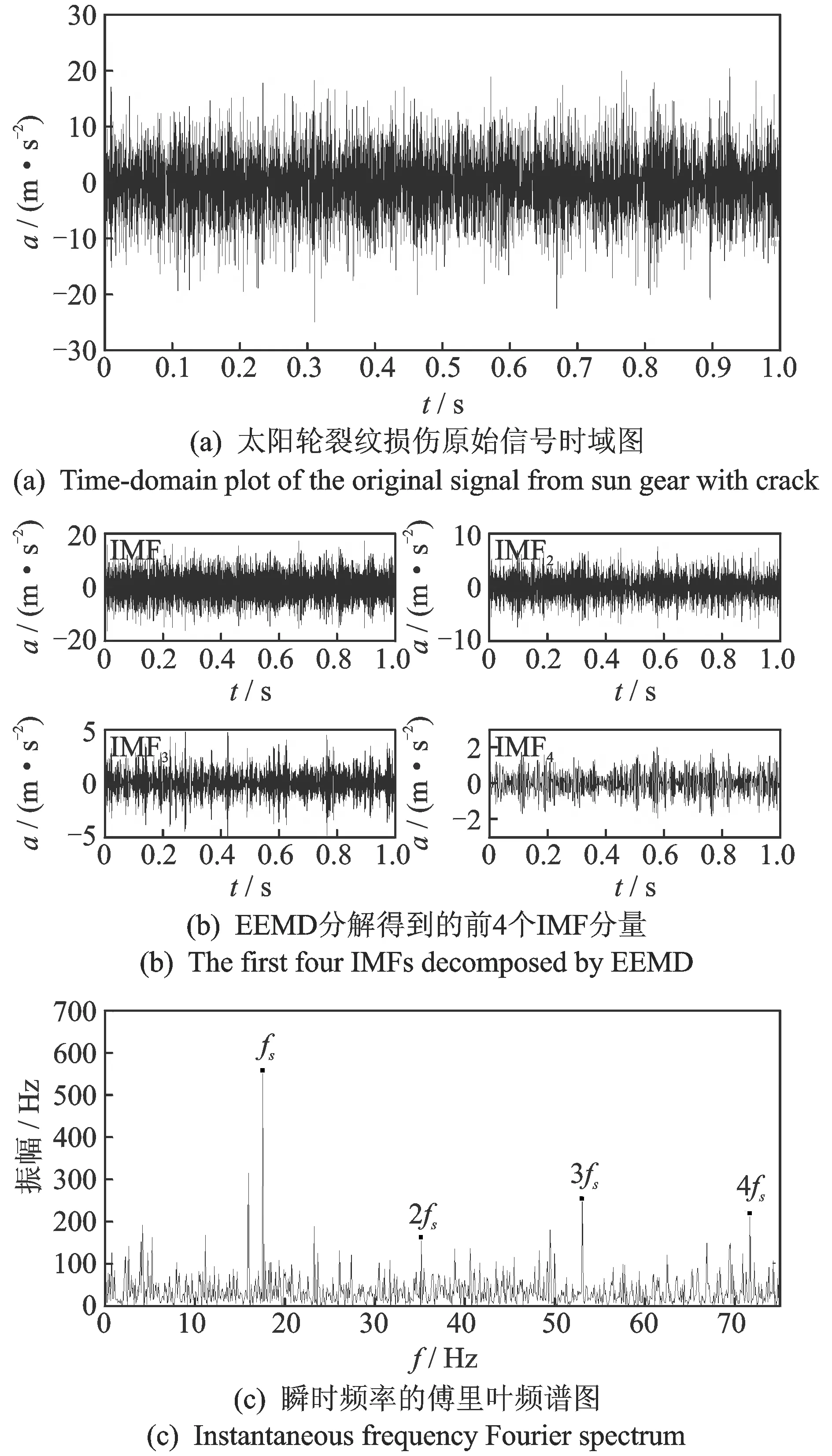
图5 太阳轮裂纹损伤定位试验分析Fig.5 Damage localization test analysis of crack sun gear

应用前面提出的基于EEMD的频率解调分析方法，处理行星齿轮式变速箱的太阳轮裂纹损伤试验信号。由表2可知，太阳轮的局部损伤特征频率fs=18.2 Hz。太阳轮裂纹损伤的原始信号时域图如图5(a)所示，可以发现裂纹损伤对振动信号的调制作用较弱，时域图中没有明显的周期性成分出现，且振幅较小，所以齿轮裂纹损伤的特征信息很难提取。图5(b)为原始信号经EEMD方法分解得到的前4个IMF分量的时域图。图5(c)为借助基于EEMD的频率解调分析方法得到的瞬时频率傅里叶频谱图(其纵坐标仅具有相对意义)，可见峰值主要出现在横坐标的18.2，36.4，54.6和72.8 Hz等处，即太阳轮的局部损伤特征频率fs及其倍频nfs处，而且fs处的峰值占主导地位。这些特征表明太阳轮产生了局部损伤，符合做试验时的实际情况，实现了行星齿轮式变速箱中太阳轮裂纹损伤的定位。

4.3 齿圈裂纹损伤定位实例分析

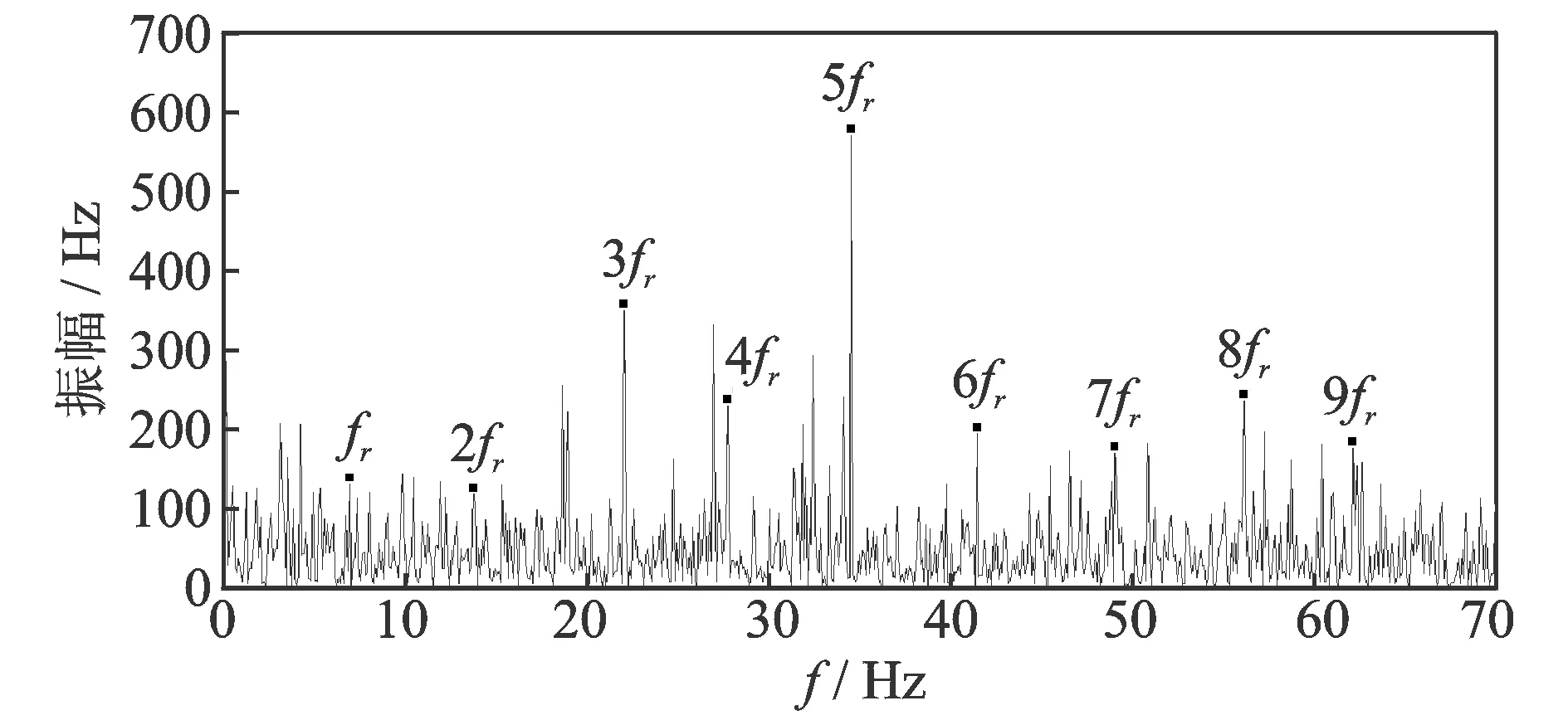
图6 齿圈裂纹损伤瞬时频率的傅里叶频谱图Fig.6 Instantaneous frequency Fourier spectrum of the ring gear with crack

图6为基于EEMD的频率解调分析方法得到的齿圈裂纹损伤的瞬时频率傅里叶频谱图(其纵坐标仅具有相对意义)，可见峰值主要出现在齿圈的局部损伤特征频率fr(由表2知，fr=7 Hz)及其倍频nfr处，而且3fr，5fr，6fr，7fr和8fr处的峰值占主导地位。这些特征表明齿圈产生了局部损伤，与做试验时的实际情况相符。

4.4 行星轮裂纹损伤定位实例分析

图7为基于EEMD的频率解调分析方法得到的行星轮裂纹损伤的瞬时频率傅里叶频谱图(其纵坐标仅具有相对意义)，可见峰值主要出现在行星轮的局部损伤特征频率fp(由表2知，fp=8.7 Hz)及其倍频nfp处，而且fp，4fp，8fp和11fp处的峰值占主导地位。由于行星轮损伤信号的传递路径比太阳轮的更长，导致其损伤信号的能量在传递过程中衰减更多；而且行星轮同时与另外两个齿轮啮合，振动信号的噪声成分更加复杂，所以行星轮的损伤特征频率最难提取，图7中的杂频干扰现象最严重。这些特征表明行星轮产生了局部损伤，与做试验时的实际情况相符。

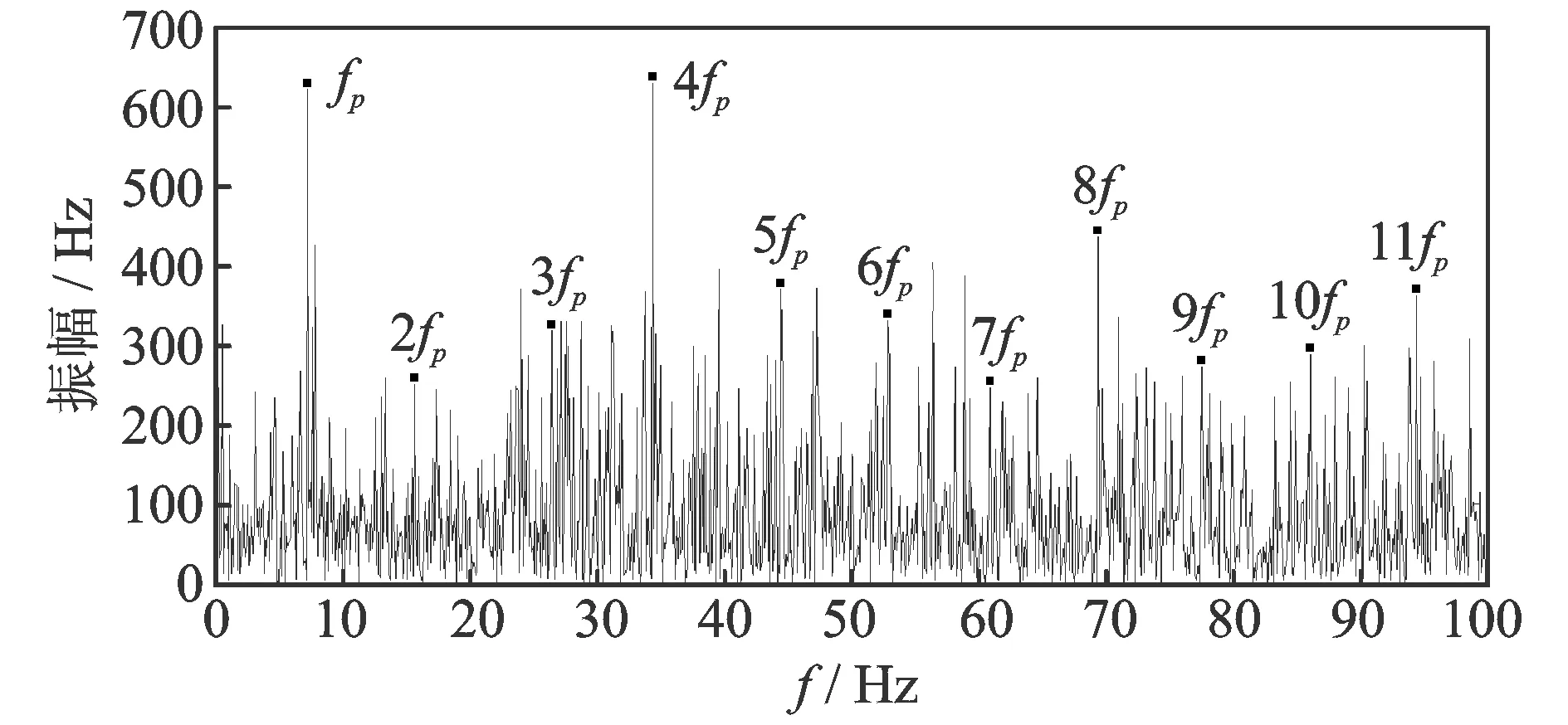
图7 行星轮裂纹损伤瞬时频率的傅里叶频谱图Fig.7 Instantaneous frequency Fourier spectrum of the planet gear with crack

5 结 论

1) 建立了行星齿轮式变速箱齿轮局部损伤振动信号模型，提出了基于EEMD的齿轮局部损伤频率解调分析方法，同时结合仿真分析和试验分析，证明了模型和该方法的准确有效性。

2) EEMD方法可以将非平稳、复杂的变速箱振动信号分解为单分量的IMF信号，并能有效改善EMD方法存在的模式混叠问题。

3) 基于EEMD的齿轮局部损伤频率解调分析方法，能成功提取太阳轮、齿圈和行星轮裂纹损伤的特征频率，实现了行星齿轮式变速箱中齿轮裂纹损伤的定位。但该研究方法的局限性在于未能实现齿轮局部损伤的定量分析，不易确定局部损伤的具体程度(如断齿、裂纹、点蚀)。

[1] 桂勇, 韩勤锴, 李峥,等. 风机行星齿轮系统齿轮裂纹故障诊断[J]. 振动、测试与诊断, 2016,36(1):169-175.

Gui Yong, Han Qinkai, Li Zheng, et al. The fault diagnosis of cracks in the planetary gear system of wind turbine[J]. Journal of Vibration, Measurement & Diagnosis, 2016,36(1):169-175. (in Chinese)

[2] Li Guoyan, Li Fangyi, Liu Haohua, et al. Fault status assessment for fault diagnosis of a multistage planetary gear set based on dynamic simulation and experimental analysis[C]∥Smart Innovation, Systems and Technologies, Sustainable Design and Manufacturing 2016. Germany: Springer International Publishing, 2016:673-686.

[3] Li Guoyan, Li Fangyi, Wang Yifan, et al. Fault diagnosis for a multistage planetary gear set using model-based simulation and experimental investigation[J]. Shock & Vibration, 2016,23(1):1-19.

[4] 桂勇, 韩勤锴, 李峥,等. 变速行星齿轮系统故障诊断方法[J]. 振动、测试与诊断, 2016, 36(2):220-226.

Gui Yong, Han Qinkai, Li Zheng, et al. Fault diagnosis of planetary gear system under time-varying speed conditions[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(2):220-226. (in Chinese)

[5] Rajeswari C, Sathiyabhama B, Devendiran S, et al. Diagnostics of gear faults using ensemble empirical mode decomposition, hybrid binary bat algorithm and machine learning algorithms[J]. Journal of Vibroengineering, 2015, 17(3):1169-1187.

[6] Žvokelj M, Zupan S, Prebil I. EEMD-based multiscale ICA method for slewing bearing fault detection and diagnosis[J]. Journal of Sound & Vibration, 2016, 370:394-423.

[7] 孙曙光, 庞毅, 王景芹, 等. 一种基于新型小波阈值去噪预处理的EEMD谐波检测方法[J]. 电力系统保护与控制, 2016, 44(2):42-48.

Sun Shuguang, Pang Yi, Wang Jingqin, et al. EEMD harmonic detection method based on the new wavelet threshold denoising pretreatment[J]. Power System Protection and Control, 2016, 44(2):42-48. (in Chinese)

[8] 陈虹屹, 王小敏, 郭进, 等. 基于 EEMD 奇异熵的高速道岔裂纹伤损检测[J]. 振动、测试与诊断, 2016, 36(5):845-851.

Chen Hongyi, Wang Xiaomin, Guo Jin, et al. High-speed turnout flaw detection based on EEMD singular entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(5):845-851. (in Chinese)

[9] Feng Zhipeng, Zuo Mingjian. Vibration signal models for fault diagnosis of planetary gearboxes[J]. Journal of Sound & Vibration, 2012, 331(22):4919-4939.

[10]冯志鹏, 褚福磊. 行星齿轮箱故障诊断的频率解调分析方法[J]. 中国电机工程学报, 2013, 33(8):112-117.

Feng Zhipeng, Chu Fulei. Frequency demodulation analysis method for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(8):112-117. (in Chinese)

[11]Lei Yaguo, Lin Jing, He Zhengjia, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical Systems & Signal Processing, 2013, 35(1-2):108-126.

[12]张超, 陈建军, 郭迅. 基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J]. 中南大学学报:自然科学版, 2012, 43(3):216-220.

Zhang Chao, Chen Jianjun, Guo Xun. Gear fault diagnosis method based on ensemble empirical mode decomposition energy entropy and support vector machine[J]. Journal of Central South University：Natural Science Edition, 2012, 43(3):216-220. (in Chinese)

[13]何正嘉, 陈进, 王太勇, 等.机械故障诊断理论及应用[M]. 北京: 高等教育出版社, 2010: 74-83.

[14]王一凡. 浮动式齿圈行星齿轮箱齿轮故障振动频谱模型研究[D]. 济南: 山东大学, 2016.

10.16450/j.cnki.issn.1004-6801.2017.03.002

国家高技术研究发展计划(“八六三”计划)资助项目(2013AA040204)

2016-12-20；

2017-02-04

TH113； TH132.4

刘浩华，男， 1993年2月生，硕士生。主要研究方向为再制造振动检测。 E-mail: liuhh0223@163.com