例题选择：从“浅层练习”走向“深度素养”

【摘要】例题的价值体现不仅要有增加知识、培养能力、启迪智慧的“基本功效”，还应该具有一定的“深度目标”：让学生能够在自主探索、灵活思辩中培养思维习惯、发展创新意识和提升数学素养.本文以例题选择为抓手，从依据课程标准，提升数学素养；重视例题选择，增强创新意识；落实目标达成，关注学生发展三个角度进行了思考，指向“让每一个学生都能够得到不同的数学体验和发展”.

【关键词】例题；创新；数学素养；学生发展

一直以来，我们很喜欢用“授人以鱼，不如授人以漁”来说明数学教学中蕴含的道理.其中，用“鱼”表示知识，用“渔”表示知识获得过程中的方法、思想等[1].数学教学中的例题，基本上都有高度抽象、高度概括和高度凝练的特征，因此，我们在进行例题教学时，不仅要有巩固知识、规范过程、锻炼能力的浅层思考，更应授人以渔，有着理解本质、领悟意蕴、提升素养的深度目标.近期，备课组内就集体备课中的例题选择进行了专题研讨，感想颇多，现整理成文，与同行交流、商榷.1初备例题

在八年级上册“三角形全等的判定方法”学习结束时，我们拟组织进行一堂判定方法综合习题课，旨在巩固学生对几种全等判定方法的掌握，培养学生综合运用的能力，提升学生数学学习意识，让每一个学生都有一定的收获.备课组任老师先给出了课堂教案“主备”内容，其中选用了如下三个例题：

例1：如图1.（1）若AB=CD，AD=BC，求证：∠A=∠C；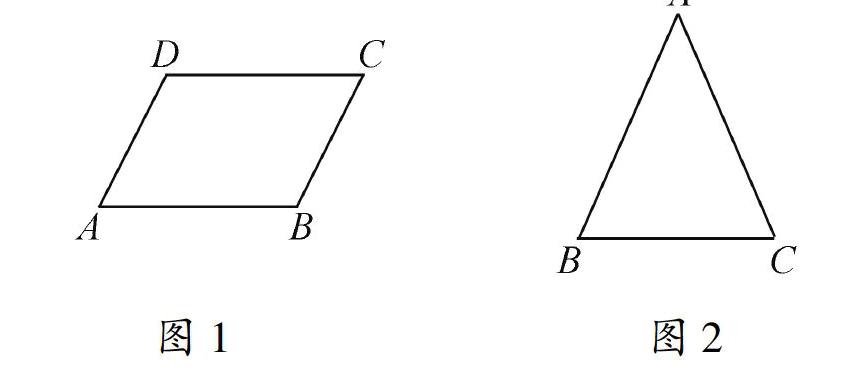

（2）若AB∥CD，AB=CD，求证：AD∥BC；

（3）若AB∥CD，AD∥BC，求证：AB=CD；

（4）若∠A=∠C，AB∥CD，求证：AD=BC.

例2：如图2，已知：AB=AC，求证：∠B=∠C.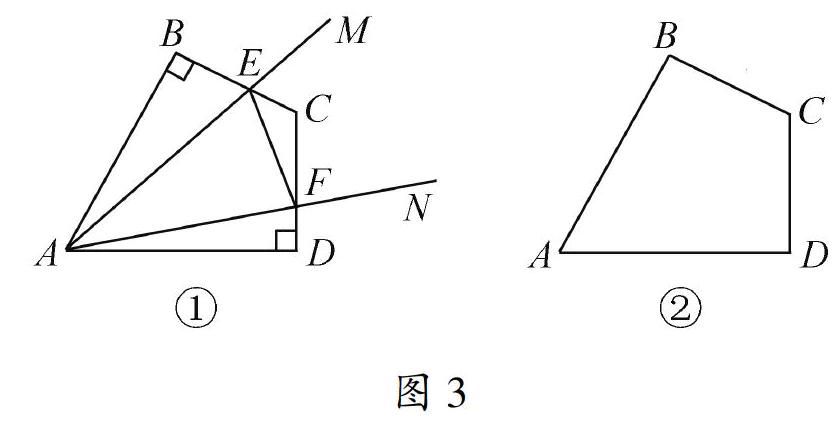

例3：如图3，在四边形ABCD中，AB=AD，∠B=∠D=90°，∠BAD=60°.现将一个30°角（∠MAN）的顶点落在点A处.

（1）如图3①，当该角的两边分别与BC、CD边相交于E、F时，求证：EF=BE+DF；

（2）现在将∠MAN绕点A进行旋转，其两边分别于BC、CD边的延长线相较于点E、F，那么（1）中的结论是否仍然成立？若成立，说明理由；若不成立，试探究线段BE、EF、DF之间的等量关系，并加以证明.

任老师给出了三个例题的选择意图：

选择例1的意图是想考查学生对四种不同全等判定方法的掌握情况，题目呈现简单易懂，知识点考查方向明确，内容基础，学生易于上手，预计独立完成正确率80%以上.

选择例2的意图主要有：相对于例1的一图多问，例2是一题多解，不同的同学可能会通过不同的方式进行解答，能够体现解答的多样性，培养学生一题多解的意识.此外，在几何学习中也常常要用到类似的“等边对等角”或“等角对等边”的知识，可以先铺垫，为学生后继学习做好准备，也为优秀学生自主学习提升知识助力.

选择例3的意图主要有：构造二次全等，介绍如何证明两条线段的和等于第三条线段的具体方法（即截取法和延长法），并让学生认识和体会如何在复杂图形中选择和判别全等三角形，会参考原有图形，根据题意画出变式问题的图形.2问题研讨

问题是思考的起点，也是研究的心脏.为了更好地研究这堂课，既尊重任老师的劳动，又能为老师们的二次备课提供帮助，从章建跃老师的“三个理解”出发，备课组提出了以下几个研讨问题：

（1）这节习题课的教学目标是什么？如何达成这样的目标？当堂能否达成？

（2）例题的知识层面达到了，但数学综合学力的培养还不够，有了“鱼”而少有“渔”.例题呈现形式有些陈旧，不够开放和新颖.

（3）从我校学生学情出发，选择例题应该有一些层次性.例3的选择目的性很明确，能够加深学生对二次全等的认识，但与前两题相比跨度较大，图形相对复杂，综合性很强，且在证明两条线段的和等于第三条线段的具体方法上有缺点，思路单一，不能够同时运用截取法和延长法两种方法解题.学生识别复杂图形的能力，理解运动变化，学会变式思考等能力还没有达到这个层次，在刚刚学习几种判定方法的情况下就处理这样的习题，明显要求过高，不太适宜.

（4）如何调整更合理？让学生的学习能力、学习意识更强，对数学更有兴趣，更愿意参与思考、参与问答，确保每一个学生都有一定的收获.3重新选择

典型例题的价值体现不仅仅是全面地考查所学知识，达成课堂目标，起到增加知识、培养能力、启迪智慧的“基本功效”[2]，更要有一定的“深度目标”，让学生在自主探索、灵活思辩、提升思维中，达到发展创新意识和提升数学素养的高度.因此，经过思考，我们对例题作了适度调整，期望能够在围绕原有思考的基础上逐步提升，巩固所学知识，拓宽解题视野，提升数学学力.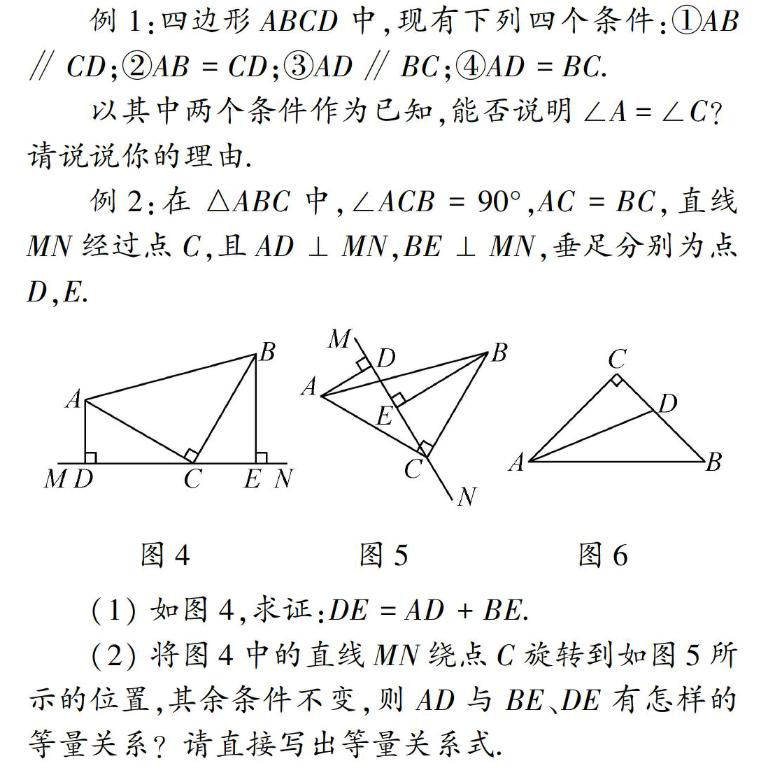

例1：四边形ABCD中，现有下列四个条件：

①AB∥CD；②AB=CD；③AD∥BC；④AD=BC.

以其中两个条件作为已知，能否说明∠A=∠C？请说说你的理由.

例2：在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN，BE⊥MN，垂足分别为点D，E.

（1）如图4，求证：DE=AD+BE.

（2）将图4中的直线MN绕点C旋转到如图5所示的位置，其余条件不变，则AD与BE、DE有怎样的等量关系？请直接写出等量关系式.

例3：已知：如图6，△ABC中，∠ACB=90°，CA=CB，AD平分∠CAB，交CB于点D，

求证：AB=AC+CD.

不难看出，例题调整前后对比，更有新意、有方法、有思维，更灵活、更实效.立足于教材、立足于通法、立足于过程，重视了基本知识技能的复习，重视了思考策略的优化，重视了解题方法的渗透，更重视了学生数学素养的提升.

（1）三个例题基本图形简洁，层次分明，梯度明确，难易适中，既有知识的复习，又有能力及素养的要求，符合学生的认知规律，有助于学生的理解和掌握，让不同的学生会有不同的收获，预计基本目标达成度高.

（2）例1更改了呈现形式，显得灵活多变，但解题思路依然很明确，既能够考查不同的全等判定方法，又有不能证明全等的“尴尬”（如①④和②③组合就不能够证明全等），学生在解决知识应用的同时，需要增加一个组合、猜想的过程，这就是能力立意的展现，让不同的学生有不同条件的组合，不同程度的思考，不同角度的体验.

例2增加了一个典型题，源于课本，让学生初步了解有“两条线段的和等于第三条线段”这样的证明题，并可以通过全等得到“转化”：将两条“小线段”放到一条“大线段”上来.这样的构造学生不难理解，课堂学习效果应该很好.而第2小问其实是第1问题的一个深度推广，让学生动起来，从不同的图形中看同一类问题，增加了学生的观察、判别、类比、猜想、说明等体验过程，对学生能力要求相对较高.当然，对于不同层次的班级，不同学力的学生，我们也可以有不同层次的思考，对于基础班级，我建议例2的第2问重在思路的分析及第1问与第2问的类比、感知，但对于提高班级，可以进一步思考直线绕点C继续旋转的其他情况.这样可以让不同的学生有不同的收获，力求课堂效率最大化.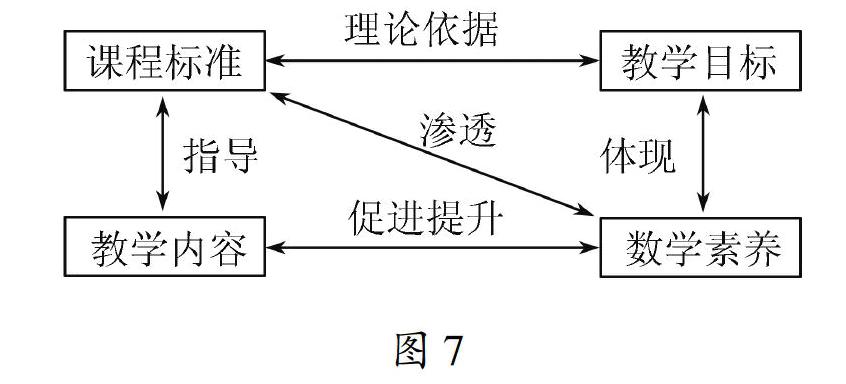

相比而言，现例3图形简洁，所换例题能够体现主备人的意图，需要构造全等，且在介绍证明两条线段的和等于第三条线段的具体方法（即截取法和延长法）中有选择性，思路不再单一，两种方法均可以用，同时也解决了原例3文字冗长、阅读困难、图形复杂、思路单一、难度过大等一系列问题.有了例2做铺垫，学生对两条线段的和等于第三条线段的证明也相对熟悉，理解相对自然，难度上也没有太大的跨度，这样的选择也符合学生已有的知识基础和认知规律.

（3）从现例1中简单、常见的辅助线，现例2中的动态变式、深度拓展，现例3中构造图形证明全等，层次清晰，由易到难，有梯度、有深度，即考查了知识层面，又有能力立意，能让学生在解决问题的同时巩固全等判定的应用.三个例题的选择，源于课本，基于本质，能够凸显课本习题的经典性和知识的应用性.现例3的选择有一定的挑战性，除了有以点及面，由知培能，由能启智的功能，更立足于拓宽学生视野，加深学生认知，提高复习的立意和品位.当然，如果学生的基本情况良好，在理解常用的“截取法”和“延长法”后，不排除增加原例3这样的习题，供学有余力的学生深度思考.

4反思教学

4.1依据课程标准，提升数学素养

学生的素养是一种稳定的内在心理品质，一种综合了的知识、能力、行为习惯等人格化特征的集中反映，是学生在学习中形成的.通过对数学的学习，使学生在数学理解，审美能力，数学表达、交流、合作能力等方面得到相應的发展[3].而数学核心素养是数学课程标准的集中体现，通过教学目标为指导，教学内容为媒介在课堂内外进行渗透与提升（如图7）.

个人认为，对于初中的数学课堂，借助适合的教学过程或典型例题、习题，通过探究的过程，合理的思辩，积极的归纳提炼，课程目标可以实现，学生的素养也必然会有所提升.

4.2重视例题选择，增强创新意识

叶圣陶先生认为：教是为了达到不需要教，教育过程是引导学生自己学习，学会自学，以至坚持终身自学的过程.长期以来，习题课是学生最不喜欢的课型之一，枯燥、机械的练习，大量重复的作业，让学生很难有热爱之情.面对原来的例1这种类型的传统习题，学生只有一个选择，那就是冲上去直接啃题.原例1中4个小题4种不同方法，看似类型全面，实则思维单一.而更改后的例1、例2都更具开放性、探究性、创新性，学生需要多方位的思考，不仅仅要寻求不同的组合、不同的思路来搭建“起点”与“终点”的桥梁，而且也需要学生在组合中选择，在选择中辨别，在辨别中思考，在不同图形、不同状态的变式中寻求新的结论，体会“变与不变”.

传统的习题教学强调知识本位，通过讲解、记忆、再练来进行夯实和巩固，但是这样一成不变的机械式学习方式老师和学生都会感到枯燥、无趣，当堂学习效果也许尚好，能够达成知识目标，但长期这样，不利于学生创新精神和实践能力的发展，让能力目标和情感目标成为空谈[3].因此，让题目新一点、活一点、开放一点，对提高学生学习兴趣、增强学生学习信心，树立勇于思考、敢于质疑等数学精神都是有好处的.当然，需要指出的是，本节课的三道例题我们可以这样选择，但不是必须选这三题，我们的思考是建立在对自己的学生相对了解的前提下的选择.题目只是媒介，课堂只是练兵场，创新意识的提升需要的不只是题目，更需要题目中的思想、思考、思辩，需要老师作为“有心人”不断的渗透和实践.

4.3落实目标达成，关注学生发展

本节习题课的教学目标比较明确，不仅要求学生能“温故”全等三角形的几种判定方法，而且希望学生能够“知新”，这个“新”，既是指数学课本知识，也是指学生的能力、方法、思想、思维、素养等.

曾经有人就教育的价值和目的如此评说：以育人为本，以兴国为旨，面向全体国民和每个学生，着眼整体人生和终身受用，培养能够全面发展、具有良好习惯的现代中国人.我们的数学教育，是科学的教育，更是人的教育.适合的才是最好的.三个新例题的选择，更适合本校学生的实际，课堂上教师不包办代替，给定学生适当的探索时间，让思维和推理搭“脚手架”，为学生提供元认知的思考方法，并重视对解题过程的回顾和总结.通过增强判断、归纳、推理意识，体会一题多变、一题多解等数学方法与技能，更多的关注了学生学习能力和学习意识的发展.

其实我们平时的教学过程也是一个不断试验、不断总结、不断提升、不断创新的过程.只有我们老师认真研究例题、习题，结合课堂目标及内容，吃透各个例题的综合功能，驾驭好题目的思想方法，才能引领学生对知识进行“统筹”“拓展”“加工”，才能达到从“浅层练习”走向“深度素养”的内在价值.而这些需要我们老师创新、灵活地教，更需要学生积极、主动地学.习题目标的综合功能需要通过典型例题来实现，这是高效学习的基础，是增知启智的前提，是培能育德的抓手，是终身学习的保障[2].这不仅是对数学知识的考查和运用，也是对学生数学解题意识、图形意识的培养，更是对应用意识、几何直观等数学素养的提升.让我们重视例题的选择，着眼于学生数学素养的提升和学生创新能力的培养，让每一个学生都能够得到不同的数学体验和收获.

参考文献

[1]裴光亚.关于“授人以鱼与授人以渔”的思考[J].中学数学教学参考，2016（3）.

[2]范建兵.从两个“度”上谈数学复习课[J].中学数学教学参考，2012（6）.

[3]张奠宙.数学教育概论[M].北京：高等教育出版社，200410.

作者简介范建兵（1977—），男，中学高级教师，主要从事初中数学教学研究.