磨刀不误砍柴深“悟”方能浅出
——初中数学“同位角、内错角、同旁内角”教学实践与思考
顾银芳
磨刀不误砍柴深“悟”方能浅出
——初中数学“同位角、内错角、同旁内角”教学实践与思考
顾银芳
同位角、内错角和同旁内角是平面几何中三个重要的角,在解题中正确识别这三种角,才能在后续的从一般到特殊的平行线知识的学习中正确判定、推理和应用。本文主要用“悟学”理念设计和组织教学过程。
预学导学悟学
“同位角、内错角和同旁内角”是一节以概念教学为主的数学课。清晰的概念是正确思维的前提,准确掌握数学概念是学好数学不可或缺的一项基本功。就本节课来说,学生只有吃透“同位角、内错角、同旁内角”这三种角的本质内涵,才能在生活中、解题中正确识别这三种角,才能在后续的从一般到特殊的平行线知识的学习中正确判定、推理和应用。数学概念概括抽象、语言简练,让学生机械识记并不难,甚至在很短的时间内就能解决,但认知心理学告诉我们:真正掌握一个概念必然要历经“由特殊到一般”“由一般到特殊”的认知发展过程,在一定意义上,学习结果的质量是由学习过程的质量决定的。在“同位角、内错角和同旁内角”的教学中,我十分注重学生学习的过程体验,用“悟学”理念设计和组织教学过程。
一、趣味导入——激发学生学习的主动性
首先,在导入新课时,回顾两条线相交时角的位置关系,再添加一条直线后,研究不同顶点处8个角的位置,激发学生的好奇心,将学生的注意力和思维活动调节到积极的状态。
其次,利用手势,跟学生互动。将两只手做成八字形(如下图),变换手势,形成同位角、内错角、同旁内角,可以让同桌互猜,避免了过多的枯燥讲解,还能加深对抽象概念的理解。
再次,让学生去观察身边的事物,从教室中寻找同位角、内错角、同旁内角,使学生感觉到数学就在我们身边,体现数学来源于生活,感受数学的价值,而且为后续平行线的学习起到很好的铺垫作用。
二、自主预学——以学案驱动学生先学初悟
教育的根本目的就是培养和发展学生的主体性。“同位角、内错角和同旁内角”是一节概念课,在进行概念的讲解时,如果直接给出它们的定义,学生不易理解,且只会通过死记硬背来识别同位角、内错角和同旁内角,效果并不好。新课标提出,教学过程是教师与学生相互作用的双边活动,而学生是数学学习的主体,教师是数学学习的组织者、引导者与合作者。我在进行这一节课的教学时,主要采用“悟学”课堂的方式,在课堂中充分发挥学生的主体性。我以导学案为媒介,通过“预学引导—合作探究—导学点拨—当堂检测”4个流程,且在教学过程中,不断交替进行“合作交流”与“导学点拨”,引导学生自主学习、合作、探究,我还对学生进行及时点拨,落实“限时讲授、合作学习、踊跃展示”的课堂教学12字方针。学生通过导学案中确定的导学目标、重难点和导学过程等自主预学,教师真正把主动权还给学生。
三、合作探究——以新情境、新问题激发学生合作思悟
在整个教学过程中,我进行了多次的合作探究。在合作探究同位角、内错角和同旁内角的概念时,我设计了如下3个表格。

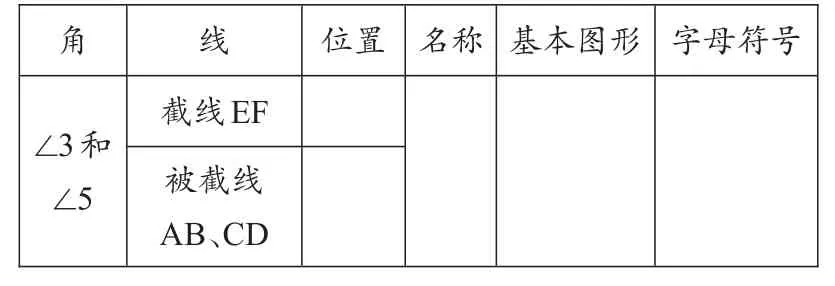
表一
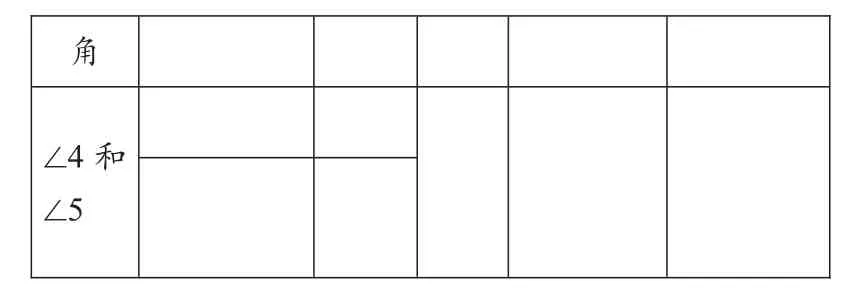
表二
表三
在研究同位角的概念时,我没有直接给出同位角的概念,而是让学生观察一组同位角与截线和被截线的位置关系,通过位置关系让学生给出同位角的定义,再通过多媒体简化图形,得到同位角的基本结构,从而找出其他同位角,再利用多媒体将这几组同位角都简化开来,让学生非常形象地观察出“F”形。在这个过程中,学生通过观察图形、探究定义、提炼和简化图形、找出基本结构,将新知识内化为自己的知识体系,从而认识同位角,完成表一。再让学生利用探索同位角的方法去探究内错角,由学生独立自主完成表二,再由师生共同小结归纳出内错角的概念和基本结构。而表三则完全交给学生,学生先自主思考,然后小组合作交流,学生在交流中思维的火花得到碰撞,同时发挥小组长的作用,让后进生也能及时掌握新知。在学生交流合作的过程中,教师及时关注各个小组的进程,着眼于学生的最近发展区,调动学生的积极性,发挥其潜能,提高学生学习几何的自信心。学生小组合作交流结束后,教师将学生的成果在全班进行展示交流,我在展示的时候,会选择中等生的导学案进行展示,然后让优等生进行点评、补充、归纳得出结论,让学生自己把概念说出来。最后再次回归原图形,总结概念,结合图形,加深对概念的理解。
四、相机引导——在必要时教师适度引导,点拨提悟
在“导学点拨”这一模块的合作探究中,教师评讲例题之后,先由学生独立思考,再组内交流,如果组内4人也无法解决,可请教其他小组。在此过程中,我穿梭在各小组之间,参与学生之间的讨论,将学生的成果及时投影,再由学生走向讲台及时补充、完善、更正、质疑,使学生在课堂上成为真正的主人。而在学生讲解中,我仔细聆听学生讲解的解题思路,适时评价、捕捉他们思维的亮点,对于他们解释不到位的地方进行补充,以引导学生掌握必要的学习方法。比如学生得到同位角这个正确答案了,我就会问怎样得到答案的,学生说是“F”形,我就再发问还有没有其他的方法,从而得到解决问题的两种途径,一是从定义出发,二是从基本结构出发。在学生学会如何从一个角出发去找出它对应的同位角、内错角和同旁内角时,教师再及时点拨,将这个角的两条边所在直线,一条作为截线,另一条作为被截线分类讨论的思想方法。在最后总结时,学生组内互相讨论,由组长总结本节课的概念和解题技巧、思想方法等。
五、当堂应用——巧设习题,在自主练习中消化领悟。
练习是数学教学过程学生实践的主要形式,是掌握知识、形成能力的重要手段。如何在复杂图形中识别同位角、内错角、同旁内角是本节课的一个难点,所以在概念讲解非常透彻的情况下,精心设计习题进行巩固新知就显得尤为重要。我先以最简单的一种情况即三线不相交时的3个习题作为例1,学生能非常快速地找出对应的同位角、内错角、同旁内角,让学生获得成功的喜悦,从而增强解决问题的信心。再以判断题的形式出题,举一反三,此时的变式则会出现四线的情况,突出其本质,让学生紧扣概念去辨析。再将简单的三线略微变形,将三线全部相交,给出被截线和截线,学会找出一个角的同位角、内错角、同旁内角,突显截线的重要性,在此基础上,再换已知条件,在三角形内部找出一个角的同旁内角,师生总结出规律,体现分类讨论的思想方法。这样根据学生水平合理编写、安排习题,调动了学生参与课堂的积极性,不断发展学生思维能力,实现“教少学多”的高效教学。而以书上例题作为例2,初步培养学生逻辑推理能力,为后续的几何证明做好铺垫。在最后我还设计了5分钟的课堂检测,习题以基础题为主,用以当堂巩固所学知识。
另外,充分用好多媒体,对于抽象的数学概念教学大有裨益。数学教学手段似乎就是那么单调,黑板加粉笔,偶尔加一些模型。由于学科自身的特点,的确没有某些学科形象、生动、具体,学起来有点枯燥无味,从而直接影响学生学习积极性。多媒体技术对文本、声音、图形、图像、动画等的综合处理及其强大的交互式特点,教学中如果能适时充分利用,丰富学生的直观感,变静止为运动,变抽象为直观,在教学上能起到事半功倍的作用。“同位角、内错角和同旁内角”这节课,在引入时,我由已学过的两线相交构成4个角的关系,利用多媒体,再增加一条线,使它动起来去截这两条直线,从而得到8个角,由旧知引入新知,“线动”使其自然过渡,拓展学生认知的时空情境,激发他们的学习兴趣。而如何在这8个角中准确找出同位角、内错角和同旁内角,并不是一件容易操作的事情,我在讲解的过程中,利用多媒体使“角”动起来,把这三种类型的角分离出去,使学生非常形象直观地观察出他们的基本结构,得到相应的字母形状“F”形、“Z”形、“U”形,从而分散难点,寻找了突破口。而在识别同位角、内错角和同旁内角的时候,最关键就是找准截线,通过图像的闪烁、色彩变化及声响效果等激发学生学习的积极性。多媒体技术适当、适度地融入数学教学中,优化了教学方式,提高了学生的学习兴趣,加深了对“三线八角”概念的理解,提高了教学效率。
总之,“磨刀不误砍柴,深‘悟’方能浅出”是我上完这堂课的最大体会。本节课展示了我校“悟学课堂”的魅力。而“预学——导学——悟学”的主线含而不露,有教无痕,以学校课模为底色,深化教学研究,自主创新,个性发展,在“去模”中实现自我超越,智慧地应用各种教学方法和手段实现课堂教学的最优化、艺术化。
(作者为江苏省南通市通州区育才中学教师)

