前瞻后顾 整体构建——以苏科版七(上)“5.4 主视图、左视图、俯视图(1)”教材解读

王晓华

前瞻后顾 整体构建
——以苏科版七(上)“5.4 主视图、左视图、俯视图(1)”教材解读

王晓华

《义务教育数学课程标准》（2011年版）指出：“数学知识的教学，要注重知识的生长点与延伸点，把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系。”基于此，笔者在近期参加的大市级评优课活动中，做了一些思考和实践，现以“5.4主视图、左视图、俯视图（1）”为例，谈谈如何对教材进行解读与设计，从而实现数学课堂的“前瞻后顾、整体构建”。

一、点全、线联、面融的教材解读

1.“点全”视角解读，关注来龙去脉。

“点全”即对某一课时的知识点进行全面解读，明白“它建立在什么基础上？它从哪里来？它是如何建立的？它将向哪里去？它有什么作用？”。基于这样的理解，在进行教学设计和实施课堂教学时，教师可以紧紧围绕“为什么要学三视图？什么是三视图？怎么看（画）三视图？学三视图有什么作用？”来展开，按照这样的知识发展线索帮助学生全面理解。

考虑到主视图、左视图、俯视图的相关知识在小学、初中、高中各个学段都有所涉及，难度又呈螺旋式上升，所以教师在教学中应立足学生已有经验，准确把握教学重难点。同时，考虑到七年级学生的抽象思维能力还有待发展，教学时仍需引导学生通过观察思考、动手实践，发展正确的空间观念。在知识拓展过程中，不妨探讨一下简单几何体三个视图的规范画法，这一方面符合“学生的最近发展区”的理念，另一方面也为下一学段的学习埋下伏笔。这样，各学段的知识便可形成一个相互联系的整体，学生也会对空间图形形成整体认识。

2.“线联”视角解读，串联前后知识。

“线联”要求充分关注本课时的知识与整个知识体系中其他知识的联系，将前后知识串联起来，追求新知的自然生成，时刻体现一条整体的知识线。

现实世界中呈现在我们眼前的物体，较多地可以抽象成立体图形，而小学、初中研究较多的是平面图形，学好平面图形可以更好地为以后学习复杂的立体图形打基础。基于这样的理解，在引入环节，教师可抓住新旧知识的联系，通过前一节课的复习，从“展开与折叠”的视角研究立体图形与平面图形出发，有效地过渡到本节课研究的方向。在总结环节，教师再从“分解与组合”的视角对立体图形与平面图形之间的关系出发，进行归纳与思想方法的提升——本节课由空间物体联想到对应的平面图形，反过来，还可以用平面图形即三视图描述立体图形——从而揭示下一节课的研究方向，留下生长式的课堂小结。

3.“面融”视角解读，提升数学素养。

“面融”即把某一课时的知识从“四基、四能”的整体层面加以解读。这里选择从宏观的角度解读教材，按照“生活—数学—生活”的顺序进行设计。

教师可选择具有现实意义的生活情境，激发学生的兴趣，引导他们由生活问题联想到其中蕴含的数学哲理。然后，让他们懂得用数学的眼光探究，需要从几个方向观察简单物体，使其感受概念提出的合理性。最后，再从数学回到生活，通过本课的知识与方法，解释生活中的现象并且学会解决实际问题；同时，还可以引申到哲学的高度，鼓励学生今后可以用数学的视角思考生活中的事物和现象。

二、基于教材解读的教学设计

基于以上的教材解读与分析，笔者进行了如下教学设计：

1.回顾旧知，方法引领。

师：前面我们经历了将现实世界中的物体抽象成数学中的立体图形的过程，但在从小学到初中的数学学习中，我们研究得更多的是平面图形。那么，我们怎样才能更好、更全面地认识立体图形呢？

（生回忆，教师板书。）

师：事实上，认识立体图形与平面图形，除了展开与折叠以外，还有没有其他的方法呢？这就是本节课我们要探讨的问题。

2.创设情境，聚焦“视角”。

（1）以图激趣，不能从单一方向观察事物。

师：大家看图1，猜猜他们是什么关系？再看图2，从中你得到什么启发？

图1

图2

小结：一般情况下，只从一个方向观察，无法准确判断物体的特征。

（2）古诗引入，多角度观察。

（投影古诗《题西林壁》:横看成岭侧成峰，远近高低各不同。不识庐山真面目，只缘身在此山中。）

师：《题西林壁》这首诗给了我们什么样的数学启发？

小结：从不同方向欣赏庐山的美，我们可以领略到不同的景致。这虽是一首诗，却隐含着一定的数学知识。

3.初步认识，体会“合理”。

（1）特殊对象，展开讨论。

师：在数学中，应选择从几个方向进行观察，可以表示出简单几何体的形状特征？

（学生讨论，然后教师点拨，以长方体为例开始研究。）

小结：在几何中，通常选择从正面、上面、左面三个方向对物体进行观察。

（2）基本图形，重点观察。

（学生列举常见几何体，教师出示模型，通过观察、思考，得出从三个方向看到的图形。对于圆锥、四棱锥从上面看得到的结果，如有争议，组织学生重点探讨。同时，教师强调并示范“如何看”。）

4.引出概念，获取新知。

（教师引出三个视图的概念，学生说出基本图形的三视图。）

师：如果把圆柱水平放置在桌面（实物演示），它的三视图还和原来一样吗？如果改变圆锥摆放位置呢？

5.利用新知，解决问题。

（1）立体图形，三视视角。

师：从不同方向观察桌面上放着的1个长方体和1个圆柱体，指出图（1）（2）（3）分别是从哪一个方向看到的？对应的是什么视图？

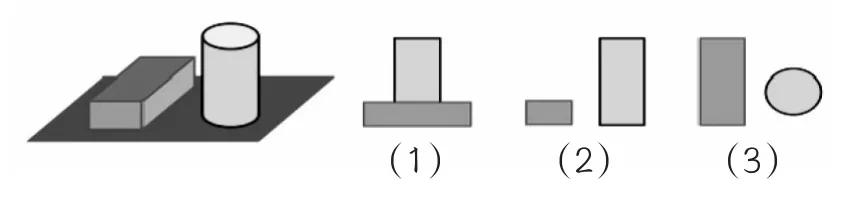
师：圆柱体和长方体的摆放位置不变，仅仅改变观察者站的位置，结果有没有变化？

小结：从单个的基本几何体到组合体三视图的研究，遵循由易到难的原则。前面改变几何体的摆放位置进行探究，此处改变观察者的观察位置来探究对应的视图，明确物体的三视图不是固定的。

（2）加深理解，寻找对应。

师：根据已给的视图，在括号内填出相应的名称，并补出剩余的视图。

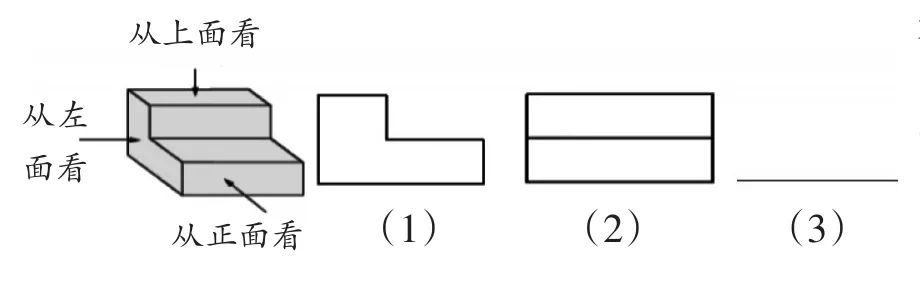
小结：为了加深对三视图的理解，通过图形基本元素的确认来判断视图并补出剩余的视图。

（3）拓展提高，强调规范。

师：如何画出几何体的三视图？请大家以长方体为例展开讨论。

（学生描述各个视图，教师示范作图。）

师：进一步思考三个视图分别反映哪个方向上的尺寸，并且探究它们之间的关系？

小结：概括出三个视图长、宽、高之间的关系，从而也明确了画图时对三个视图位置的安排的合理性。

练习：画出下列几何体的三视图。

（在几何体上标注数据，目的就是便于学生相互检查。学生先独立画图，然后相互讨论、纠正，最后教师投影学生的作品，并总结画图的要点。）

（4）学以致用，回归生活。

（课件展示部分零件及汽车、飞机的图纸，出示校园的图片。）

师：如果你是设计师，怎样才能让建筑师按你的意图来建造呢？

6.前后呼应，总结提升。

师：通过本课的学习，谈谈你的收获与体会？

（学生从知识本身、思想方法与生活哲理等方面进行总结。）

（教师从分解与组合的角度进行再归纳，同时引出下节课要探讨的问题。）

（作者为无锡市中小学浦叙德名师工作室成员，无锡市新安中学教师）

领衔人点评：

“主视图、左视图、俯视图”教学共分“由立体图形得视图”与“由视图得立体图形”两课时进行。根据“点全—线联—面融”式课时解读的要求，探寻知识的源头和方法显得非常重要，本文的解读为设计指明了方向。生活中有许多例子和经验都表明，认识事物可以从局部到整体，也可以从整体到局部，“三视图”正好是一个整体到局部的过程。另外，前面学过的立体图形与平面图形“展开与折叠”中“分解与组合”的思想方法，也为本课的学习奠定了坚实的基础。这样的设计直接服务于课堂教学的长效。