换个角度理解

文︳廖晓岚

换个角度理解

文︳廖晓岚

人教版六年级上册中的数学广角“数与形”中有如下例题：计算

教材使用的方式是数形结合（如图所示）。

但图形中始终存在的那一小块扇形或那一小段线段不在例题所示的加数之内，也就等于直观地告诉学生，总和不等于1。无限是不能用直观表达出来的，学生通过观察图形，认为不等于1是非常自然的，甚至许许多多的成年人也会认为不等于1，何况小学生呢？

有人这样考虑：

=…

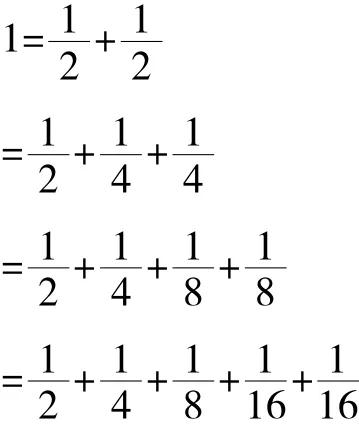
这样不断下去，似乎能说明问题。但学生会发现，这里的每一个加法算式的结果都是1，但这里的任何一个加法算式都与题目中的加法算式不同。

当然，我们可以说一句：这是极限。但用一个“极限”对付过去，与其说是解决了问题，不如说是回避或拒绝了讨论——凭什么极限就要相等？因此，如何使小学生对例题有一个比较清晰的认识，老师们需要动动脑子。

在教学实践中，笔者试图带领学生换个角度理解问题。

首先，我们要认识，不是随便无限多个数都可以相加的。比如1+2+3+4+5+6+…就没有意义。所谓没有意义，是说你不可能找到一个数，能作为这个加法算式的和。这个不难理解：随你找个什么数，这个和式都会超过，而且是远远地超过你所找的那个数。

第三，我们来确定这个和。或者说，我们要找一个数，使得这个数作为例题中这个无限多个数相加的加法算式的和是合理的。

显然，这个数不应该大于1。事实上，以上图中的圆形图形为例。圆的面积用1表示，则上述加法算式的每一个加数都对应着一个小扇形。容易理解，所有的小扇形都在圆内，都是从圆中分割出来的，没有重复。它们的和不可能超过圆。

此时，还有两个可能，或者有一个小于1的数可以作这个和，或者1就是这个和。下面我们来说明，任何一个小于1的数，都是不可能作这个和的。

容易知道，这样的分析，不仅仅对这两个数管用，对任何一个小于1的数a，我们都可以确定，这样不断地加下去，和总会超过a的。

从上面的讨论可以看出，如果我们承认有些情况下，无限多个数也是可以相加的，比如，我们承认是有意义的，那么，我们就必须承认

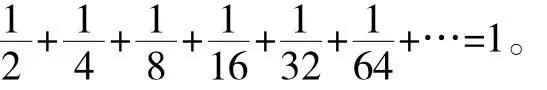
必须说明的是，由于这个算式涉及无限，而无限对于小学生来说，是很难理解的。因此，无论采用什么样的办法，我们都不太可能将这个算式的理解变得太简单。从这个意义上讲，也许最好的办法是：在小学里暂时不讨论这个问题。

（作者单位：娄底市第六中学）