9.1平面的基本性质教案

云南省玉溪市澄江县职业高级中学 郑苏拉

课题：

平面的基本性质

教学目标：

知识目标：通过列举实例，类比直线，准确抽象出平面的特点；掌握平面的表示法和画法；理解和掌握平面的三个基本性质，会用集合的语言描述空间中点、线、面之间的位置关系。

能力目标：通过实例和多媒体进行直观教学，培养学生的观察能力和空间想象能力，培养学生在数学语言之间相互转化的能力。

情感目标：结合生活中大量的实例进行“数学来源于生活”的唯物主义观念教育，通过各种实践性解决问题的思维模式培养学生合作交流、独立思考等良好的个性品质。

教学重点：

平面的表示法与画法；平面的三个基本性质。

教学难点：

对平面的概念理解及平面的基本性质的理解与运用。

授课类型：

新授课

教具：

多媒体、直尺、三角板、笔、书等

课时：

2学时

教学过程：

一、创设问题情境，导入新课

1.观察抚摸玻璃面、墙面、桌面、黑板面你会发现它们有什么共同之处？

2.教师用多媒体展示一些平面的图片：“海平面”“冰天雪地”等。

提问：谈谈你对平面的感受？生活中还有那些事物给我们以平面的形象？

二、概念解剖分析，认识平面

认识平面：

平面是一个只进行描述而不加以定义的几何中的最基本概念之一，是平坦而且可以无限延展的图形。

1.概念辨析

（1）一个平面长4m ,宽2m.

（2）铺得很平的一张白纸是一个平面吗？那么黑板面、桌面、墙面呢？生活中存不存在真正的平面？

（3）通常80页书会比8页书厚一些，那么80个平面重合在一起时比8个平面重合在一起时厚吗？

（4）怎样理解无限延展？（类比直线）

（教师通过教室这个空间、学生的学习用具进行演示讲解）

2.总结归纳

以上问题给了我们“平面”的直观形象，不仅揭示了平面的特点：“平”“无限延展”“无厚薄”，更重要的是让学生深入的理解了平面最本质的属性：无限延展。

三、平面的基本性质

1.空间中点、直线、平面的位置关系

问题1.我们知道怎样三角形、圆等式怎样形成的，但我们可以通过怎样的方式形成平面呢？

问题2.“点动成线 线动成面面动成体”，直线可以看成是以点为元素的集合，那么平面是否可视为点构成的集合呢？可以用怎样的数学符号表示点、直线与平面之间的关系？

通过两个问题的引导，自然的利用多媒体给出点与直线，点与平面、直线与直线的位置关系及图像.

2.平面的基本性质（1）

问题1.将手中的笔假想为一条直线，将课桌面或者课本面假想为一个平面，能否摆出直线和平面只有一个交点的情况？

问题2.能否摆出直线和平面不存在交点的情况？

问题3.能否摆出直线和平面只有两个交点的情形？

性质1：如果一条直线的两点在一个平面内，那么这条直线上所有的点都在这个平面内。

问题4：你能否用图形和符号语言将性质1表述出来吗？

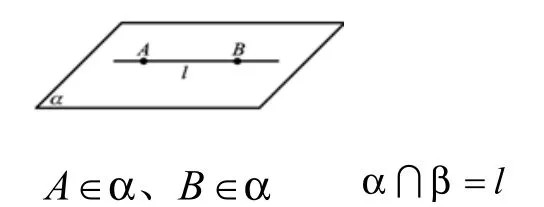
问题5：你认为性质1有什么用？

平面的基本性质（2）

问题1.将手中的课本假想成一个平面，将课桌面假想成另一个平面，能否摆出没有交点的情形？

问题2.能否摆出平面和平面只有一个交点的情形？

总结：

性质2：如果两个平面有一个交点，那么它们还有其他的公共点，这些点的集合是经过此公共点的一条直线.

问题3.你能用图形和语言符号将性质2表述出来吗？

问题4.你认为性质2有什么用？

平面的基本性质（3）

问题1.我们已经学过：两个点可以确定一条直线。这里“确定”的含义是什么？

问题2.用笔尖代表点，尝试一下至少要用几支笔的笔尖擦岂能将一页纸所代表的平面稳定的托起来？

问题3.观察笔尖在纸上留下的三个点，有什么特点？

总结：

性质3：不共线的三个点可以确定一个平面。

问题4.“不共线的三个点”还可以用其他的意思表示出来吗？

推论：（1）两条相交直线可以确定一个平面。

（2）一条直线与直线外一点可以确定一个平面。

（3）两条平行直线可以确定一个平面。

请用平面的性质说明这三个结论

工人常用两根平行的木条来固定一排物品（1）；营业员用彩带交叉捆扎礼品盒（2），都是上述结论的应用

四、运用知识 强化练习

1.“平面α与平面β只有一个公共点”的说法正确吗？

2.梯形是平面图形吗？为什么？

3.已知A、B、C是直线l上的三个点，D不是直线l上的点．判断直线AD、BD、CD是否在同一个平面内．

五、归纳小结 强化思想

本次课学了哪些内容？重点和难点各是什么？

六、继续探索 活动探究