小学图形面积问题中化归思想的教育价值

广西壮族自治区桂林市永福县龙江乡龙应民族学校 张 钰

化归方法是指把待解决的问题通过某种恰当而又可行的转化，归结为我们已经解决过的或比较容易解决的问题，从而最终获得原问题的解答的手段、方式和方法。

一、化归思想

假如在你面前有煤气灶、水龙头、水壶和火柴，你想烧开水，应当怎样去做？回答：“倒掉壶中的水，并声称我已把后一问题化归成原先的问题了。”

感悟：“把水倒掉”这是多么简洁的回答，但却说出了化归的根本特征，目的是引导我们感悟他独特的思维方式——转化。学习数学不是问题解决方案的累积记忆，而是要学会把未知的问题转化为已知的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题只有这样转化，学习数学起来就简单多了。

（一）化归的定义

化归，就是将一种形式转化归为另一种形式的过程。化归思想作为一种数学的思想方法，其基本的思维方式“不对新问题做出正面的解答，而是将新问题不断的变形，直到把它转化为能够解决为止”。

（二）化归的原则

基本原则主要有熟悉化原则、正难则反原则、简单化原则等。数的认识来源于生活，又应用于生活。比如三年级有分数的初步认识、小数的认识，四年级有大数的认识、小数的意义等，都是密切联系生活，我们在教学中应根据实际问题，转化为数学问题。

如教学四上“大数的认识”中亿以内的数时，教师就可以根据化归思想创造性地使用教材，通过创设身边的生活情境来表示数，让学生感知所学的数并不能用来表示现实的数，产生一种大数的需要。这就需要教师有丰富的知识，有一颗爱学生之心，善于跟他们交朋友，在课堂教学中，循序渐进地引导学生去理解，感悟，以及运用。

二、化归思想在图形面积教学中的教育价值

（一）有利于深刻地认识数学教学内容

在学习平面图形的面积计算时，我们通过动手操作探究长方形的面积公式，而学习平行四边形、三角形和梯形面积时，则是在已有的认知基础下进行转化探究，得出面积计算的公式。所以，在认识平面图形中就应渗透化归思想，为图形面积的计算打下基础。

（二）有利于提高学生的数学素养

掌握数学思想方法能增强学生的数学素质，数学知识离不开数学思想方法。三角形的面积，是把三角形转化为长方形或平行四边形，得出三角形的面积=底×高÷2；圆的面积：我们用剪一剪、拼一拼、旋转、平移的方法，把圆形化归为一个近似于长方形的图形。我们把没有学过的知识转化为我们已经学过的知识来解决新问题，这种解决数学问题的方法就是——化归的数学思想方法。

（三）有利于教师以较高的观点分析和处理小学教材

在三角形的面积计算中，引导学生用两个相同的三角形通过“拼一拼”的方法把两个相同的三角形拼成一个平行四边形。在圆的面积学习中运用已有的转化思想进行探究，潜移默化的运用化归的思想方法解决面积计算中的问题。

在小学教学教材中一是数学知识，它明明白白地写在课本里，是有形的；二是数学思想方法，它是渗透在知识体系中的，是潜在的。教师以较高的观点分析教材和处理教材，科学地、灵活地设计教学方法，提高课堂教学效率。例如，《圆的面积》教学中化归思想方法的渗透。教学过程如下。

1.确定“转化”的策略

预设：（出示画有长方形、正方形、平行四边形、三角形、梯形的图）

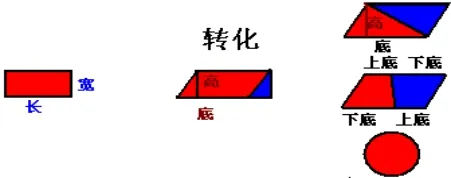
2.尝试“转化”

师：圆的面积能不能也可以化（？）为（？）来得出它的计算公式。

生：我们可以先切割，再转化。师：那又怎样切割？生：沿着它的直径切下去。

师：这样会有什么效果呢？想不想看看？（想）我们看（师演示），你们发现了什么？（生：出现了两条直的直径、线段）

师：对，刚才我们说化曲为直，终于完成了这一步，但还不够，还要化圆为方。同学们，我们已经切了一刀了，还想不想再切？（想）那怎样切？（生：沿直径竖着切。）

师：我们再切看看，这四个是什么图形？（生：是近似的等腰三角形。）

师：现在我们能不能有办法求圆的面积？

师：我们再切，然后再拼一拼看看。（先后把圆分成4等份、8等份、16等份的圆演示。）我们所拼的这些图形越来越近似什么图形？

生：这些图形越来越近似（平行四边形）长方形。

师：如果这样无限地切分下去，就慢慢地转化成了长方形是吧？

师：同学们看，老师把圆分成的64等份、128等份的圆，它们是不是更近似长方形？

3.学生合作探究，推导公式

（1）讨论探究，出示提示语

问题一：转化后长方形的长相当于圆的______，宽相当于圆的______

问题二：你能从计算长方形的面积推导出计算圆面积的公式吗？

（2）演示公式推导过程（重点详细讲解）

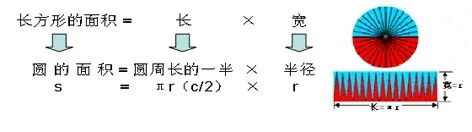
（3）揭示字母公式

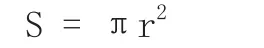
通过渗透一种转化的思想，引导学生抽象概括出新的问题可以转化成旧的知识，利用旧知识解决新的问题。生动形象地展示了化曲为直的剪拼过程。这样处理教材，有利于学生更好地理解与掌握相关数学内容，有助于学生形成良好的认知结构，学生更乐意参与数学学习。

三、小结

化归思想方法能帮助学生化未知为已知，化难为易，化繁为简，化曲为直。我国古人也说：“授人以鱼不如授人以渔”。所以，一堂真正具有思想深度的数学课，留给学生是心灵激荡的数学思考和长久受用的解决问题的数学方法，这是研究与学习数学思想方法的价值所在。