重“化”抓“法”“优”然自得——“优化”一课的教学思考与实践

◇陈新福 方 鑫

重“化”抓“法”“优”然自得
——“优化”一课的教学思考与实践

◇陈新福 方 鑫

“优化”一课是北师大版教材四年级下册“数学好玩”中的内容，共安排了两个学习内容：一是沏茶问题，二是烙饼问题。沏茶问题主要是通过学习流程图，学习几件事情“包含式”的“同时”安排进行的优化；烙饼问题主要是通过一个锅里的两张饼正反“交替式”的“同时”安排进行的优化。另外，烙饼问题还含有规律性知识内容的学习，具有较高的思维性要求。

教学中，如何引导学生从数学的角度，运用所学知识和方法寻找解决问题的策略，并达成数学思维训练等隐性的目标呢？为此，我们展开了相关的教学实践。

一、重“化”：借助直观，积累经验，感悟优化

众所周知，运筹优化对小学生来说是比较抽象的学习内容。如何让学生更好地感受、理解优化思想呢？教学中需要借助直观图、操作体验，在切身感受、亲身体验中积累经验，为优化思想的学习理解奠定基础。

1.引入新资源，对比流程图，鼓励学生在较高的起点上展开学习。

学生对要学习的“优化”内容已有一些生活经验，课前，教师可以通过调查、访谈等手段，掌握学生的学习起点，进而确定教学导入方式。

（1）现状描述。

课前，我们把教材上沏茶问题的主题图（如图1）给一些学生看，让他们说一说、画一画。

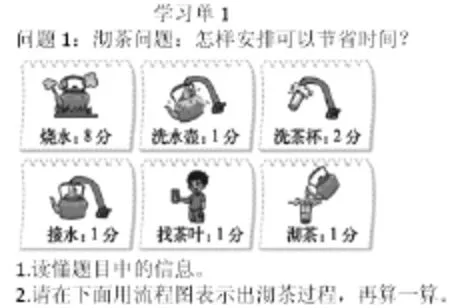
图1

结果发现，部分学生虽然不能优化，但能用较为清晰的表达方式，得出沏茶问题总时间是14分；另一部分学生则能基本解决，还能比较好地用图来表达。大体情况如下：

①生1：洗水壶→洗茶杯→接水→烧水→找茶叶→沏茶。1+2+1+8+1+1=14（分）。

②生2：找茶叶→洗水壶→接水→烧水→洗茶杯→沏茶。1+1+1+8+2+1=14（分）。

③生3：先洗水壶，再接水，然后烧水。在烧水时，可以洗茶杯、找茶叶，最后沏茶。1+1+8=10（分），10+1=11（分）。

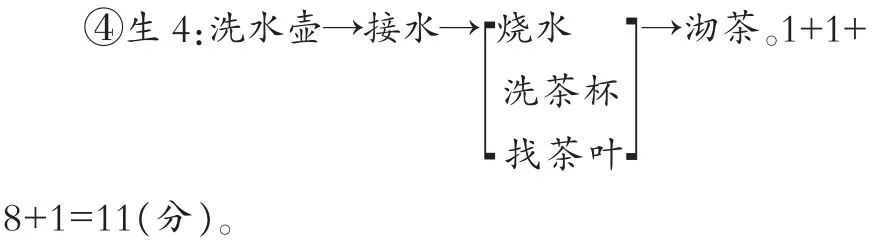
（2）教学安排。

既然部分学生可以独立解决这个问题，我们就从这一较高的学习起点展开教学。为了兼顾部分学生不知道优化的实际情况，我们特意安排小组学习交流，具体教学安排如下。

环节一：呈现情境，理解题意。

教师呈现书本里的问题1，鼓励学生读一读题，理解题的意思。

环节二：呈现解法，小组讨论。

在读题的基础上，教师呈现解法（即上面4个学生的解法），并安排小组讨论：你赞同谁的方法？说一说你的理由。

环节三：集体汇报，提炼思考。

在小组交流的基础上，教师安排集体反馈，组织学生讨论、对比，得出沏茶问题优化的实质是：烧水时，可以同时做一些其他事情，这样用时就会节省。同时，在汇报解决问题的过程中，指导表达的符号，突出简洁性的要求，学习理解“包含式”的“同时”安排进行的优化。

2.构建情境串，借助直观图，让学生在动态操作中展开学习。

（1）现状描述。

如果说前面的沏茶问题，学生具有较好的学习基础，那接下来的烙饼问题，学生的学习起点并不乐观。其原因有二：一方面，学生对怎样烙饼不熟悉，即便有的学生知道，也只是知道一个锅里烙一张饼；另一方面，一个锅里烙两张饼，正反都要烙，这个事件较难用图来刻画，更难用一幅图来表达，需要连续的几幅图才能表达完整，所以学习难度大。为此，我们认为对此内容的学习，需要直观化教学，通过动态直观操作，发展学生的符号化表达能力，切实理解“交替式”的“同时”安排进行优化的本质内涵。

（2）教学安排。

环节一：情境串联，激发学习意愿。

一般来说，一个锅里烙一张饼，烙好正面，再烙反面。今天的要求是一个锅同时烙两张饼，怎样才能尽快烙完所有饼呢？如此，通过情境串联，引发学生积极的学习意愿。

环节二：操作理解，分步展开、分步刻画更扎实。

教学中安排两个步骤：步骤1是学习烙1张饼、2张饼、4张饼等所需要的时间；步骤2提出烙3张饼，你认为需要多少时间？

在教学中，重点学习烙2张饼的内容。先借助学具理解烙饼的操作流程（如图2）。

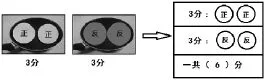
图2

通过对直观操作的再“操作”，表达刻画成按照时间先后来描述的表格图；在此基础上，再学习烙4张饼等内容。接着学习烙3张饼的情况，学生通过估计、操作、刻画，最后得到优化安排的时间（如图3）。

从上面的教学叙述我们可以知道，“化”就是一个行动，是学生参与活动的过程。通过活动明确数学条件，为学习交流提供学习材料与资源，并为数学思考、数学分析提供新的思考对象，在对比、分析、交流的过程中，发现、掌握优化的内涵。

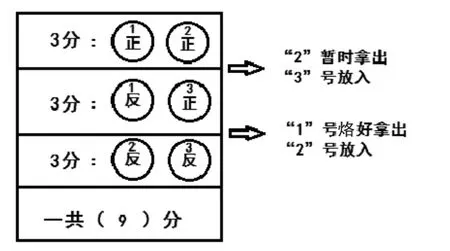
图3

二、抓“法”：紧扣难点，关注策略，提炼优化

在前面的教学描述中，我们关注了“化”，着重提出直观性的学习要求。但是，仅仅如此是不够的。因为“化”是手段，手段需要“法”来规范与牵引，这个“法”，就是指数学方法、数学思想。为此，我们认为，在活动过程中，教师还需要引发学生透过对内容的操作，体验并提炼出优化的方法，学生只有理解掌握了数学思想、方法，才算是学到有价值的数学知识。

1.对比引导，突出“优化”的符号化。

在“沏茶”问题的调研中，我们发现这个内容，对学生来说虽然不难理解，但很难用语言清晰地表达，特别是把几个事件“同时”完成，会用合理的符号表达出来的则少之又少。为此，在“沏茶”问题的学习中，通过讨论与展示学生作品，在对比、辨析中大家一致认为“生 4”的表达方法最好，把烧水和洗茶杯、找茶叶并列、竖着排列，让大家明白这三件事可以同时进行。

在“烙饼”问题中，用简洁、明确的符号来表示事件的发生过程，显得尤为重要。因为“烙饼”问题中有正反之别，加之奇数张时还需要交替进行，所以，教师在学习中安排学具操作环节，然后再讨论符号化表达，鼓励采用表格来刻画烙饼过程。

2.问题相助，提升“优化”的概念化。

优化是一个过程，不是一个固定的结论。刚才提到的符号化，更多的是指优化的直观性要求，如何引导学生由形入数，由数到式（算）呢？我们需要在教学关键处，借助数学问题的设计，来促使学生数学化思考，提炼概念。

如“沏茶”问题的教学中，当学生一致认为“生4”的表达方式好，总时间是11分时，教师提出问题：难道洗茶杯、找茶叶不用时间吗？为什么这些可以不计算到总时间里？学生讨论后知道：连续进行的一些事件所用时间是各个环节总时间的和，其中某个环节中几个事件同时进行，就取用时最多的事件所用的时间。

再如“烙饼”问题中的环节二，我们分为两个步骤展开。步骤1是学生通过直观操作得出烙1张饼、2张饼和4张饼的时间，接着提出问题：你能很快知道烙6张饼的时间吗？如果烙8张饼呢？你发现了什么规律？步骤2是当学生操作后，知道烙3张饼的时间，教师则提出：烙5张饼呢？7张呢？教师可在学生操作后，有序地提出烙更多张饼所需要的时间，引导学生离开“具体操作”，进入“头脑操作”的环节，鼓励学生关注事件背后的规律，推理形成结构化、概念化的数学思考，建构数学模式，发展学生的数学能力。

（作者单位：浙江衢州市柯城区教研室，衢州市衢江第一小学）