寻例合情 演绎明理——由『被学生问住了』谈起

◇ 李小强

寻例合情 演绎明理
——由『被学生问住了』谈起

◇ 李小强

一、缘起

1.案例1：3的倍数特征。

“李老师，你说一个数各个数位上的数的和是3的倍数，它就是3的倍数。为什么呀？”一个男生提出自己的疑问。这是在学习北师大版教材五年级 “3的倍数特征”一课时，课堂上发生的一幕，至今令我记忆犹新。

面对这个突如其来的问题，我有点儿不知所措。

但还没等我回答，就有一个“好事”的学生开口了：“这还不明白，你看黑板，老师在百数表中已经找到了所有是3的倍数的数，很明显这些数每个数位上的数的和是3的倍数呀！你还问为什么？”他洋洋得意地坐下了。

冷静下来后，我这样回答：“我们是通过寻找是3的倍数的数并研究它们的特征发现了规律，你再想一想。”学生疑惑地坐下了。

课后，回想起那一刻及我的回答，深感无力与惭愧。虽然不愿意承认，但我明白我的的确确被他问住了。

回顾我们的教学，类似的案例并不少见。

2.案例2：三角形边的关系。

北师大版教材四年级“三角形边的关系”，教材是通过如下三个问题的探讨逐步归纳出结论的。

问题1：哪一组小棒可以摆成三角形？

为学生提供4组小棒（每组3根，长度不同），学生自主尝试利用小棒摆三角形，并思考能或者不能摆成三角形的原因是什么。

问题2：怎样的3根小棒能摆成一个三角形？

在问题1的基础上进一步观察、研究、讨论每组中能够摆成三角形的3根小棒之间的关系或特征。还可以从反面思考：怎样的3根小棒摆不成三角形？

问题3：明晰三角形三边的关系。

借助算一算、比一比的活动，发现能够摆成三角形的三边长度之间的关系。

课堂很顺利，最终得到“三角形任意两边之和大于第三边”的结论。

面对这个结论，学生并没有提出异议。但在教学研讨时，一位听课教师提到：课堂上，能不能从另外一个角度来解释（或证明）三角形中任意两边之和大于第三边呢？

二、寻例合情

仔细分析两个案例，不难看出教材的安排与设计思想是一致的，都是从具体的实例（实验）出发，通过观察、操作、猜想、归纳等方法得出一个可能性的结论，即合情推理。由于合情推理更加符合小学生的认知水平，实例具体、形象直观、易于理解，所以现行教材编写更倾向于合情推理。

正是因为合情推理是通过经验和直觉得来的可能性结论，它的准确性就受到很多因素的影响。如，在探索3的倍数特征时，由于学生有了2和5的倍数特征的探索经验，于是有一部分同学会给出“个位是3、6、9的数就是3的倍数”这样的错误结论；再如，探索三角形三边关系的操作中，由于学生操作的不规范或者测量中的较大误差，结论也会不尽相同。

显然，上面那些客观存在的经验、因素都会制约结论的准确性。即便通过观察、操作、猜想、归纳得到的结论是准确的，但它毕竟还是可能性结论，其正确性也有待进一步验证或证明，所以无论是案例1中学生的问题，还是案例2中听课教师的疑问，都不是无中生有，需要认真思考并研究。

谈到推理，《数学课程标准（2011）》指出：推理是数学的基本思维方式，一般包括合情推理和演绎推理……在解决问题的过程中，两种推理的功能不同，相辅相成：合情推理用于探索思路，发现结论；演绎推理用于证明结论。

可见两种推理方式是相辅相成的。合情推理是必要的，它从数学的具体案例中抽象出一般性结论，见证了数学的发展；演绎推理也是必需的，它能判断合情推理中发现的结论是否正确、严谨，让数学的发展更加“健康”。所以，在小学数学教学中，虽然应该侧重于合情推理，但也不能偏废了演绎推理。

三、演绎明理

1.对3的倍数特征的证明。

案例1中学生提出了自己的问题，我并没有给出合理的回答。这个学生整节课一直专注于思考自己的问题，第二天他给了我这样的理由：

如果用 ab代表一个两位数。由于a在十位上，b在个位上，这个数就可以记作10a＋b，进而等于（9+1）a＋b＝9a+（a＋b）。因为9a一定是3的倍数，所以只要a＋b是3的倍数，那么两位数ab就是3的倍数。这样就证明了：一个数各个数位上的数的和是3的倍数，它就是3的倍数。

因为在研究3的倍数时，我们是在100以内寻找3的倍数的，所以学生以任意两位数为例证明了这个结论在百以内是正确的。

学生对问题的钻研精神和深刻的思考，让我佩服。按照他的思路，如果是任意一个正整数，证明如下：

假设n=asas-1…a2a1a0是任意一个正整数，0≤as≤9（as是整数），s＝0，1，2，3……

那么n就可以表示为：

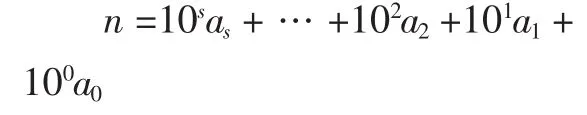
对n变形得：

在算式 （10s-1）as＋…＋（102-1）a2＋（101-1）a1中，每一项都是3的倍数，它们的和也是3的倍数。所以，只要保证as＋…＋a2＋a1＋a0是3的倍数，则正整数n就是3的倍数，而as＋…＋a2＋a1＋a0表示的就是n的各个数位上的数的和。

所以，一个数各个数位上的数的和是3的倍数，它就是3的倍数。

2.三角形三边关系的证明。

在北师大版《教师教学用书》中关于“三角形三边关系”还提供了另一种思路：首先通过情境图认识“两点之间线段最短”，再画出两个点并在两点之间画出一条线段和若干条折线（每条折线只有两条线段），这样这条线段和折线就构成了一个个三角形，那么折线的长度（两条线段的长度和）一定大于这条线段的长度。

所以，三角形任意两边之和大于第三边可以追溯至“两点之间所有连线中线段最短”，也就是说我们可以通过“两点之间所有连线中线段最短”证明“三角形任意两边之和大于第三边”。对于任意三角形ABC中，证明过程如下：

∵两点之间的所有连线中线段最短

∴在△ABC中AB＋BC＞AC

同理可得：在△ABC中AC＋BC＞AB，AC＋AB＞BC

∴三角形中任意两边之和大于第三边

这样的演绎推理，既证明了结论的正确性，又能让学生明白研究数学的方法。

数学是思维的科学，小学数学教学虽然更重视直观形象的感知与反复尝试的体验，但逻辑思维水平的提升也是不可缺少的。曹培英老师说过：如果一个人只相信眼见为实，不知道思维的能动性可以通过推理帮助人类突破感觉、经验、尝试的局限性，那就是个人素养的一大缺失。所以在小学数学教学中，尤其是高年级教学中需要将合情推理与演绎推理相结合，在学生能理解与接受的基础上，从这两个角度给学生更加合理的解释，引导学生建立正确的思维观，为学生的可持续发展奠定良好的基础。

（作者单位：陕西咸阳市秦都区陕西师范大学奥林匹克花园学校）