经历活动过程 积累无形经验——《烙饼问题》教学实录与思考

俞瑶璟 朱长生

一、情境引入，明确问题

师：（呈现主题图）从图中你发现哪些数学信息？

生：每次只能烙2张饼，两面都要烙，每面需要3分钟，要烙40张饼。

师：你找的信息很完整！每次只能烙2张饼是什么意思？

生：一只锅同时只能烙2张饼。

师：也就是说烙一次最多烙熟几个面？

生：2个面。因为烙2张饼，一张饼一个面，所以能烙熟2个面。

师：怎样才能尽快吃上饼？

生：时间尽量短。

师：烙熟40张饼最少时间是多少？

【思考：对数学信息正确透彻的理解是本课的关键，通过提出关键性问题促使学生读懂信息，感知烙饼的过程，为下一步研究问题奠定扎实的基础。】

二、自主探究，转化问题

1.揭题并板题：烙饼问题。

师：40张饼数字有点大，怎么研究？

生：先从小一点的数据来研究。

师：你想到了好办法，可以先研究1张饼、2张饼、3张饼。这是从小数据开始研究。

（板书：小数据）

2.同桌合作，操作汇报。

（1）学生利用手中的学具（3张圆片）摆一摆，完成表格后和同桌交流。

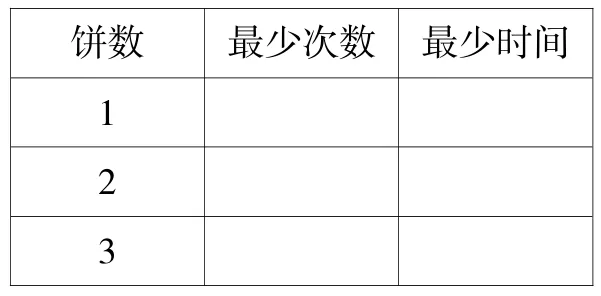
饼数最少次数最少时间1 2 3

（2）全班同学交流汇报。

师：烙1张饼要烙几次？需要几分钟？

生：烙2次，需要6分钟。正面3分钟，反面也要3分钟。

师：烙2张饼最少需要几次？最少时间是?

生：2次，最少需要6分钟。

生：第一次是1正2正，第二次1反2反。

师：像这样的烙法我们给它取个名字叫“2张同时烙”。

师：烙1张饼和2张饼为什么时间都是6分钟？

生：2张饼是同时烙，而1张饼空间有浪费。

师：从烙的过程看，烙2张饼有没有更加省时的方法？为什么？

生：没有。每次锅里都是2张饼，空间没有浪费。

师：看来每次锅里有2张饼时间是最少的。

师：3张饼最少烙几次？最少时间是多少？

生：最少4次，最少时间是12分钟。

（学生上台边摆边说：第一次1正2正，第二次1反2反，第三次3正，第四次3反）

生：最少3次，最少时间是9分钟。第一次1正2正，第二次1反3正，第三次2反3反。

师：像这样有交替过程的烙法我们叫“3张交替烙”。

师：后一位同学对前一位同学的方法进行了优化，想到了最佳方法。

师：两张饼我们用了2张同时烙的方法，3张饼用了3张交替烙的方法。

（3）思考烙4、5张饼。

师：刚才我们学习了2张同时烙和3张交替烙。请你思考烙4张饼怎么烙？最少次数是多少？最少时间呢？

生：最少4次，时间是12分钟。第一次1正2正，第二次1反2反。

师：也就是说这两张饼采用了什么方法？

生：2张同时烙的方法。

生：第三次3正4正，第四次3反4反，后面又是2张饼同时烙的方法。

师：刚才这位同学是怎么烙的？

生：转化成了两次2张同时烙的方法。

师：那可以记作：2，2。5 张饼怎么转化呢？

生：先烙3张饼，采用3张交替烙的方法，另2张饼采用2张同时烙的方法。最少次数5次，时间15分钟。

师：记作：2，3。回顾我们探索烙4张饼和5张饼的过程，你们用了什么重要的数学方法？

生：用到了转化，转化成刚才学过的两种最简单的烙法：2张同时烙和3张交替烙。

（4）运用转化方法。

师：6张饼怎么转化呢？

生：转化成3次2张同时烙，也就是 2，2，2。

生：我有不同想法，转化为2次3张交替烙。也就是3，3。最少次数6次，最少时间18分。

师：7张饼怎么转化？

生：转化为2次2张同时烙，最后3张交替烙。记作2，2，3。最少次数7次，最少时间3×7=21（分）。

师：饼数不断增加，咱们全班同学都要吃到饼，40张怎么转化呢？

生：20 个 2。

生：12个3加上2个2。

生：13个3加上1个。

生：我认为他的想法不对。因为最后一个单独烙的话，那最后两次锅里没有两张饼的，最后两次只有1张饼，空间有浪费，不是最短时间。

师：你们这么多方法，什么是一样的？

生：最少次数40次，最少时间120分钟。

师：那如果是998张饼呢？

【思考：当学生面对数据比较大的时候，习得了一种分析问题的方法：从小数据着手。在研究烙1、2、3张饼时，每位同学都有充分的时间和空间，借助小圆片这一学具将烙的过程外显化。正是学生经历的这一探索过程才让学生掌握2张同时烙和3张交替烙两种最优化的方法，操作过程让学生的思维变得形象直观。对3张饼怎么烙时间最短我们还看到了优化思想的渗透。当然数学思维不该仅仅停留在形象思维上，还必须上升到抽象思维。研究烙4、5张饼不采用操作，这激发了学生的思维，想到了转化这一重要的数学思想。整个环节，学生动手操作，动脑思考，充分展示在操作中思考，在过程中学习。】

三、探索规律，建立模型

1.发现规律。

师：998张饼要去转化就太麻烦了，而且转化的方法也多种多样。你是否能从表格中发现奥妙呢？

生：饼数是多少，最少次数就是多少。

生：除了1以外，其余的饼数=最少次数。

师：为什么呢？

生：2张饼，2×2=4个面，需要2×2÷2=2次。

生：3张饼，2×3=6个面，需要2×3÷2=3次。

生：4张饼，2×4=8个面，需要2×4÷2=4次。

师：n张饼呢？

生：n×2 个面，n×2÷2=n次。最少时间是n×3分钟。

师：n可以等于1吗？为什么？

生：1张饼要烙2个面，最少时间是6分钟，而按照这样算是3分钟，所以n＞1。

2.运用规律。

师：俞老师班里有45位学生，每位学生一张饼，最少时间是多少？

生：45×3=135（分钟）。

师：二年级210人，每人一张饼，最少时间是多少？

生：210×3=630（分钟）。

师：还有其它方法可以验证“饼数=次数”这个规律吗？老师带来了一种方法，现在我把这个锅对折起来，烙1次烙熟了几张饼？

生：对折以后相当于一张饼的正反面同时烙熟了，n次就把n张饼烙熟了。

师：烙饼问题刚开始看确实是有一定挑战性的任务，但只要找对策略，就能事半功倍。回顾一下，我们是怎么探索的？

（板书：小数据→转化→规律）

生：先研究 1、2、3 张饼的烙法，在探索4、5、6张饼时用到了转化，最后找到规律，可以求任意张饼数。

【思考：前面学习的两种最优烙法和转化的重要思想为后面发现规律奠定了基础。学生借助观察、归纳、概括获得了计算最少时间的方法，即时间=饼数×一面需要的时间，这个算法其实是一个模型。学生在学习过程中，真正经历了自己探索，自己总结结论，自己概括模型，充分展示了“过程教育”。】