Ti-Ni形状记忆合金复合悬摆减震系统性能试验研究

王社良， 余滨杉， 樊禹江， 杨 涛

(1. 西安建筑科技大学 土木工程学院，西安 710055；2. 长安大学 建筑学院，西安 710061)

Ti-Ni形状记忆合金复合悬摆减震系统性能试验研究

王社良1， 余滨杉1， 樊禹江2， 杨 涛1

(1. 西安建筑科技大学 土木工程学院，西安 710055；2. 长安大学 建筑学院，西安 710061)

系统研究了Ti-Ni形状记忆合金丝应力-应变曲线、特征点应力、耗能能力、等效阻尼比等随材料直径、应变幅值、加载循环次数的变化规律，结果表明：丝材直径的增加会导致SMA丝力学性能趋于劣化；当应变幅值为6%、加载循环次数达15次时，可获得滞回性能良好、工作稳定的SMA丝材。将训练后所得SMA丝材，利用其超弹性特性，结合调谐质量阻尼器基本工作原理，设计制作了一类可便于拆卸的SMA复合悬摆减震系统。针对该类减震系统，完成了相应的性能试验，分析了该系统自振频率、质量振子与受控结构间的相位关系、等效阻尼力随振子质量、摆杆长度的变化规律，结果表明：该减震系统在正弦波和真实地震激励下质量振子与受控体结构之间相位关系始终较好的保持在150°～180°之间；同时，等效阻尼力随外荷载幅值的增大，控制效果更加明显。综上，该系统能够简便应用于结构振动控制之中，并提供稳定、高效的阻尼力，从而保护结构免于强动力灾害。

超弹性特性；形状记忆合金复合悬摆减震系统；相位关系；等效阻尼力

消能减震装置是实现结构被动控制，保护/减轻结构在地震、强风等强动力灾害作用下振动损害的有效措施。目前，传统的被动消能减震装置常采用橡胶隔震、黏滞流体、黏弹性材料、低屈服点金属等[1]，该类型阻尼器在实际工程的应用中存在诸多问题，如材料易老化、长期可靠性差、残余变形不可恢复等[2]。同时，亦无法满足既有建筑(如古塔等亟待保护的建筑结构等)进行简便安装、保护效果明显等需求，因而其应用范围受到了一定的限制。

形状记忆合金(Shape Memory Alloy，SMA)作为一种新型智能材料，具有独特的形状记忆效应、超弹性效应和高阻尼特性等特点[3]，因而在结构振动控制领域受到广泛的关注。国内外诸多学者针对SMA基本材料性能及其在结构振动控制中的应用进行了相关研究，Corbi等[4]比较了SMA拉索和弹塑性拉索对单层框架结构弹塑性振动反应的控制效果，指出SMA拉索在抑制结构振动的同时赋予了结构良好的复位功能。陈云等[5]提出一种新型耗能增强型SMA阻尼器，该阻尼器的滞回环饱满，耗能能力强，性能优于SMA拉索的耗能效果。任文杰等[6]利用 SMA提出一种新型自复位SMA阻尼器，并对安装有该阻尼器的框架结构进行了理论分析，结果表明阻尼器能有效抑制结构的位移、层间位移和残余位移，但会增大结构加速度。

本文基于SMA超弹性特性等理论，系统研究SMA应力-应变、耗能能力等随材料直径、应变幅值、加载循环次数的变化规律，确定适用于阻尼器开发的SMA材料。结合调谐质量阻尼器基本工作原理，设计制作了一类可便于拆卸的SMA复合悬摆减震系统。通过改变摆锤质量、摆杆长度两种参数，对该减震系统进行了性能试验研究，分析了该系统质量振子与受控结构间的相位关系和等效阻尼力的变化规律，验证了该套系统应用于结构振动控制中的有效性。

2 SMA丝材力学性能试验

2.1 试验概况

本文系统研究了SMA丝材直径、应变幅值、加载循环次数各因素对其应力-应变曲线、特征点应力、耗能能力、等效阻尼比等的影响规律，试验工况，如表1所示。

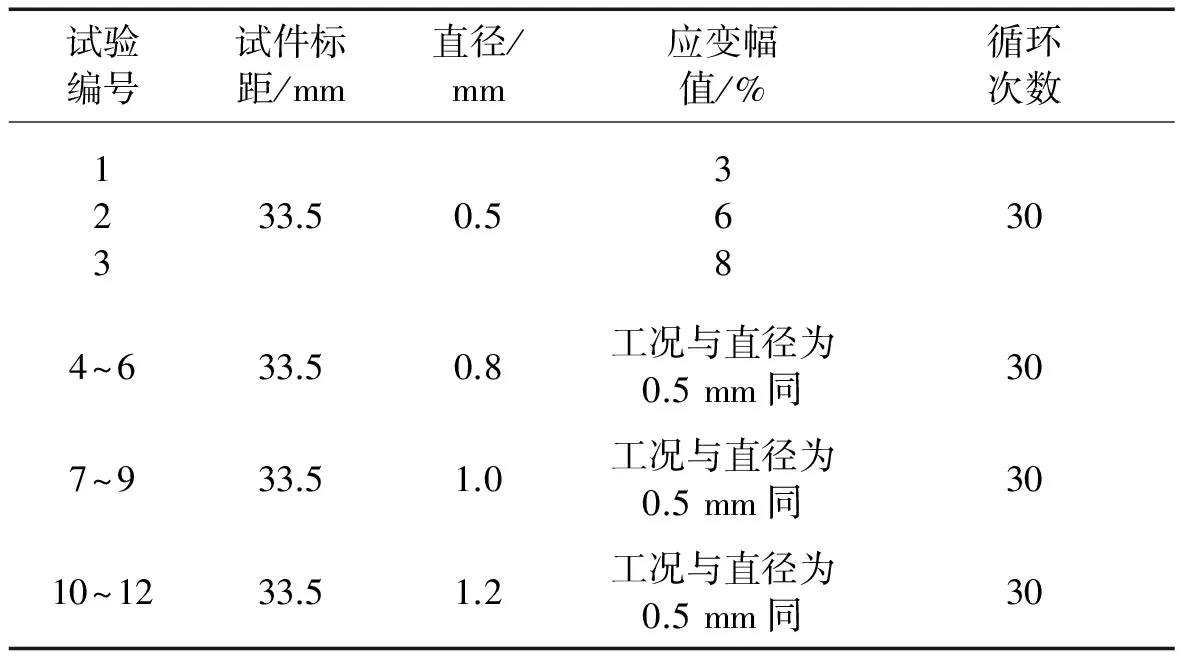
表1 SMA丝超弹性性能试验工况

试验中SMA丝由西北有色金属研究院赛特金属材料开发有限公司提供，化学成分为Ti-50.8at%Ni，试件长度300 mm，有效长度100 mm。相变温度：Mf为-42 ℃，Ms为-38 ℃，Af为-13 ℃，As为-9 ℃。本试验在西安理工大学材料科学实验室进行，试验采用弘达HT-2402电脑式伺服控制材料试验机。该试验机最大拉、压荷载为100 t，荷载精度为±5%，轴向变形由位移引伸计测量，标距为33.5 mm；试验中加载/卸载模式均采用定速率加载/卸载；其中加载时以丝材应变达到预设应变幅值作为终止条件，卸载时以丝材所受轴向力小于5 N作为终止条件，同时对每种工况循环加载30圈。

2.2 试验分析

对常温下为奥氏体的SMA丝进行加载/卸载循环试验，其单圈应力-应变曲线如图1所示。加载段以应力-应变曲线平台开始点作为特征点a；以经过加载平台，加载段曲线斜率明显增大点作为特征点b；以应力应变下降开始偏离线性关系的点作为特征点c；应力-应变曲线在卸载末期，从非线性变为线性，以应力应变开始近似成比例下降的点为特征点d[7]。

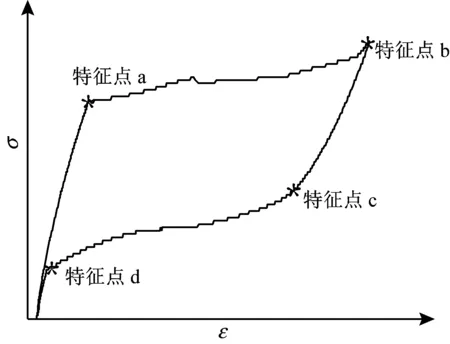
图1 本构曲线特征点

2.2.1 丝材直径的影响

分别选取直径为0.5 mm、0.8 mm、1.0 mm、1.2 mm的SMA丝，加载应变幅值为6%，以研究材料直径对SMA丝材力学性能的影响，所得结果，如图2及表2所示。随着材料直径的增大，SMA丝的应力-应变曲线趋于平滑，材料的累计残余变形增大，各特征点应力均有不同程度的降低；直径从0.5 mm增大到1.2 mm，特征点a，b，c，d的应力分别降低了27.81%、20.74%、25.21%和65.27%。材料直径小于0.8 mm时，SMA丝的耗能能力和等效阻尼比变化较小；材料直径大于0.8 mm时，二者随直径的增大，呈明显减小的趋势，其中耗能能力降低了21.19%，等效阻尼比降低了22.96%。

2.2.2 应变幅值的影响

选取直径为0.5 mm的SMA丝，以分析不同应变幅值对SMA丝力学性能的影响，所得结果，如图3和表3所示。随着SMA丝应变幅值的增大，特征点a，b，c的应力变化不大，而特征点d的应力随着应变幅值的增大而减小，表明随着应变幅值的增大，SMA的应力应变曲线趋于饱满，耗能能力增大。其中，当应变幅值由3%增大至8%时，SMA丝的单圈耗能从4.46 MJ·m-3增大到20.76 MJ·m-3，耗能能力增大了近4.7倍。等效阻尼比在应变幅值小于6%时，阻尼比显著增大；当应变幅值大于6%时，阻尼比变化较小，说明虽然SMA丝的绝对耗能能力随着应变幅值的增大而增大，但是其耗能效率在应变幅值为6%左右时达到最优。

(a) 应力-应变曲线的变化

(b) 特征点应力的变化

(c) 耗能的变化

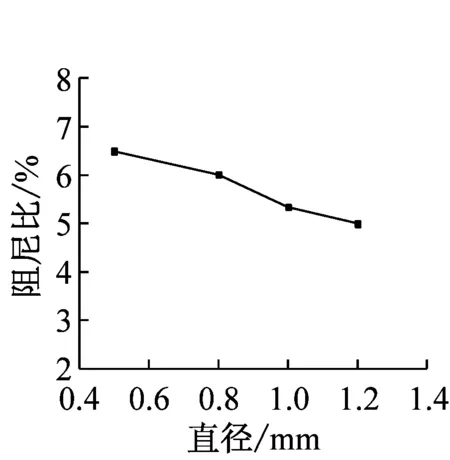
(d) 等效阻尼比的变化

表2 不同直径对应的奥氏体SMA丝力学性能参数值

(a) 应力-应变曲线的变化

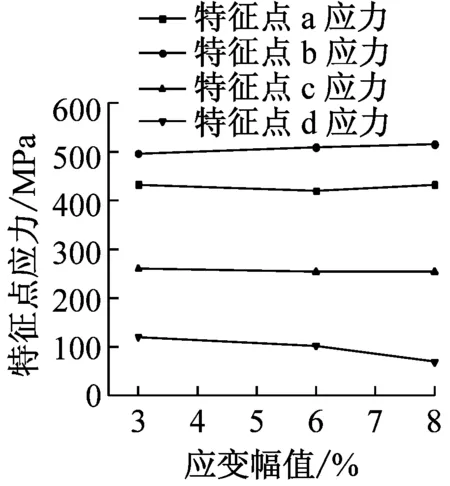
(b) 特征点应力的变化

(c) 耗能的变化

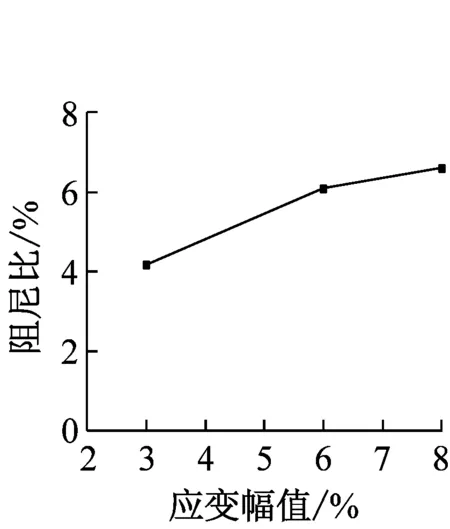
(d) 等效阻尼比的变化

应变幅值σa/MPaσb/MPaσc/MPaσd/MPaΔW/(MJ·m-3)ζa/%3%426．90496．56260．65120．964．464．186%420．17509．30254．65101．8612．706．098%432．90515．66254．6570．0320．766．60

2.2.3 循环加载次数的影响

选取直径为0.5 mm，应变幅值为6%的SMA丝，以分析不同循环加载次数对其力学性能的影响，所得结果，如图4及表4所示。随着循环次数的增加，SMA丝应力-应变曲线逐渐变光滑，累计残余变形逐渐增大，单次循环的残余变形减小，第16循环的单圈残余变形仅为0.003%；针对马氏体相变，经过15个循环降低了140.06 MPa，30个循环后，特征点a的应力降低了171.89 MPa， 其中前15个循环降幅占总降幅的81.49%；同样，特征点b的应力下降也主要发生在前15个循环。对奥氏体相变，经30个循环后，特征点c，d的应力、分别降低了57.30 MPa和25.46 MPa，降幅为20.93%和14.28%，而前10个循环的降幅分别占总降幅的88.89%和75.02%，特征点c，d的应力在第10循环以后趋于稳定。同时，SMA丝的单圈耗能和等效阻尼比随循环次数逐渐减小，30个循环后，单圈耗能降低了2.405 MJ·m-3，降幅达35.16%；等效阻尼比降低了1.95%，降幅达31.91%，前期循环耗能和等效阻尼比下降较快，15个循环后耗能能力和等效阻尼趋于稳定。

由此可见循环次数对奥氏体SMA丝的力学性能影响很大。为此，在实际的工程应用中，为了得到SMA材料稳定的超弹性性能，必须预先对其进行循环加载训练，即：加卸载循环15圈左右后，SMA丝力学性能可趋于稳定。

(a) 应力-应变曲线的变化

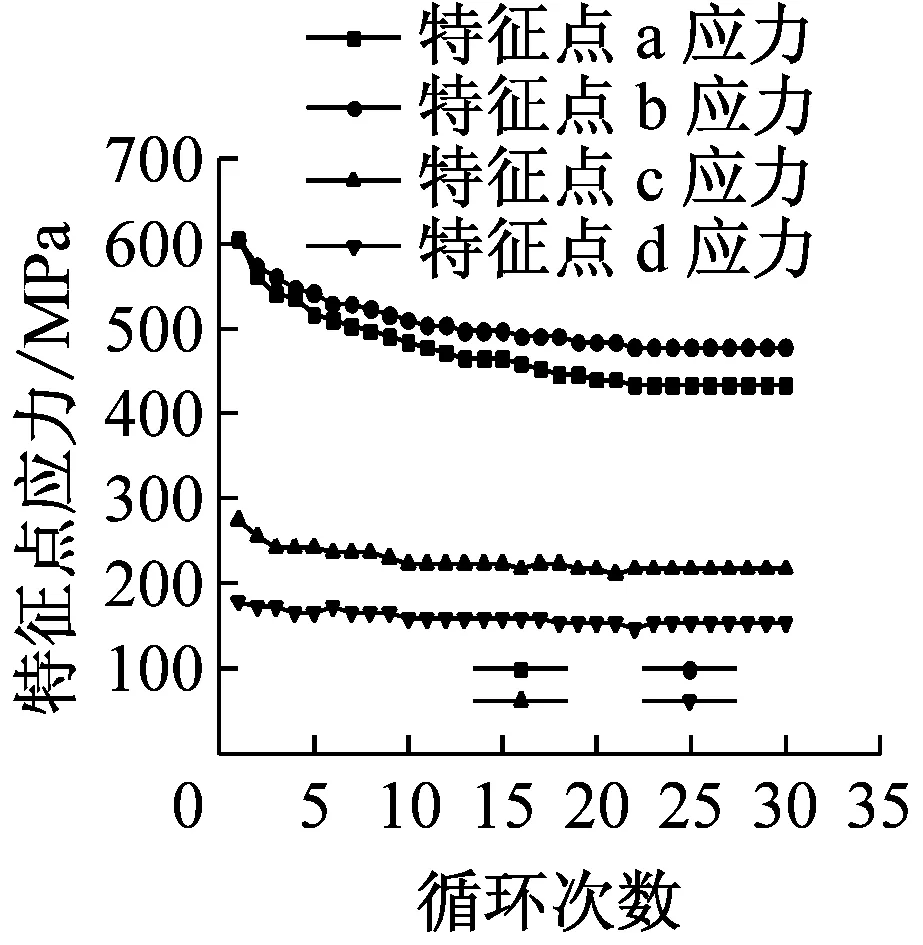
(b) 特征点应力的变化

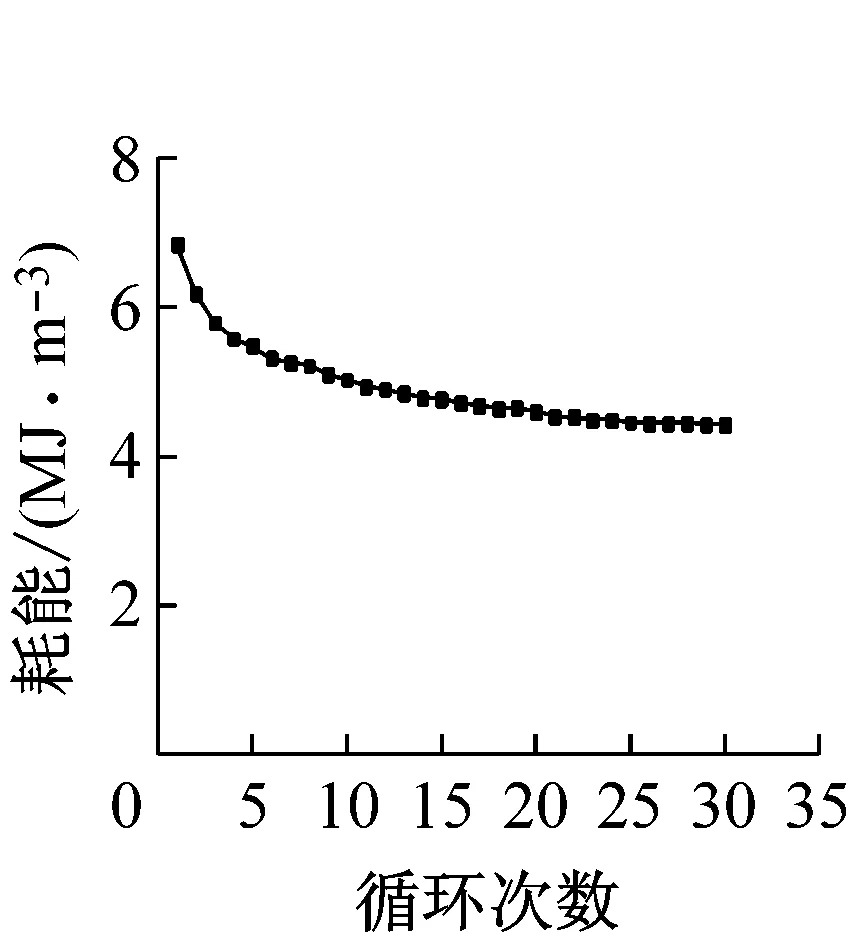
(c) 耗能的变化

(d) 等效阻尼比的变化

循环次数σa/MPaσb/MPaσc/MPaσd/MPaΔW/(MJ·m-3)ζa/%1604．79604．79273．75178．256．8436．112560．23572．96254．65171．896．1905．813541．13560．23241．92171．895．7965．445515．66541．13241．92165．525．4815．1810483．83509．30222．82159．155．0354．7615440．73496．56222．82159．154．7694．4820439．27483．83216．45152．794．6034．3725432．90477．46216．45152．794．4614．1830432．90477．46216．45152．794．4384．16

3 SMA复合悬摆减震系统设计

考虑上述SMA丝材性能试验结果，利用SMA丝的超弹性性能，结合悬摆减震原理，本文设计并制作了一类SMA复合悬摆减震系统，模型如图5所示。该系统由质量振子、摆杆、单向铰、滑块、训练后SMA丝及转向滑轮等几个部分构成。其基本构造设计如下：① 采用单向铰作为摆杆上端的连接点，单向铰垂直于摆动平面，摆杆上端设置穿入孔，可自由穿入单向铰转轴，转轴两端设置螺纹，中间足够光滑，以保证摆杆自由转动。② 摆杆吊点两端设置阻尼片，阻尼片外侧转轴分别套装等刚度弹簧，通过紧固螺栓改变阻尼片的预压力，可调整悬摆减震系统的阻尼。③ 摆杆下端与质量振子中心处的螺孔相连，质量振子上对称设置多个安装点，方便调整质量。④ 质量振子两侧与形状记忆合金丝一端设置的滑块相连，另一端通过转化接头与钢索连接后固定于结构。以一次循环为例，说明该阻尼器的工作原理，当悬摆由右向左摆动时，可带动右侧滑块沿水平滑道运动并拉动右侧SMA丝材产生相对位移Δε，此时左侧的SMA处于松弛状态，当质量振子恢复到平衡位置时SMA丝放松，其经历了一个耗能循环过程，形成饱满的滞回曲线，实现了对结构的耗能过程，同时质量振子的惯性力通过钢索反作用到结构上，对结构的振动产生控制作用，使结构的振动反应得到衰减。同理当质量块由左侧摆向右侧时，则是左侧滑块被带动从而使左侧丝材拉紧并产生位移，右侧丝材松弛。在质量块的摆动过程中，SMA丝材经历了由拉紧到收缩的循环过程，构成了饱满的滞回曲线，实现了对结构的耗能过程。

图5 SMA复合悬摆减震系统示意图

4 SMA复合悬摆减震系统性能试验研究

SMA复合悬摆减震系统性能试验主要分析了频率、质量振子与振动台台面之间相位关系、等效阻尼力等随振子质量、摆长的变化规律，工况如表5所示。该试验在西安建筑科技大学结构与抗震试验室WS-Z30-50精密振动台上完成，如图6所示。试验时在质量振子处设置X向位移和加速度传感器；同时，为分析减震系统与台面的振动相位关系，在台面处X向亦设置位移、加速度传感器。

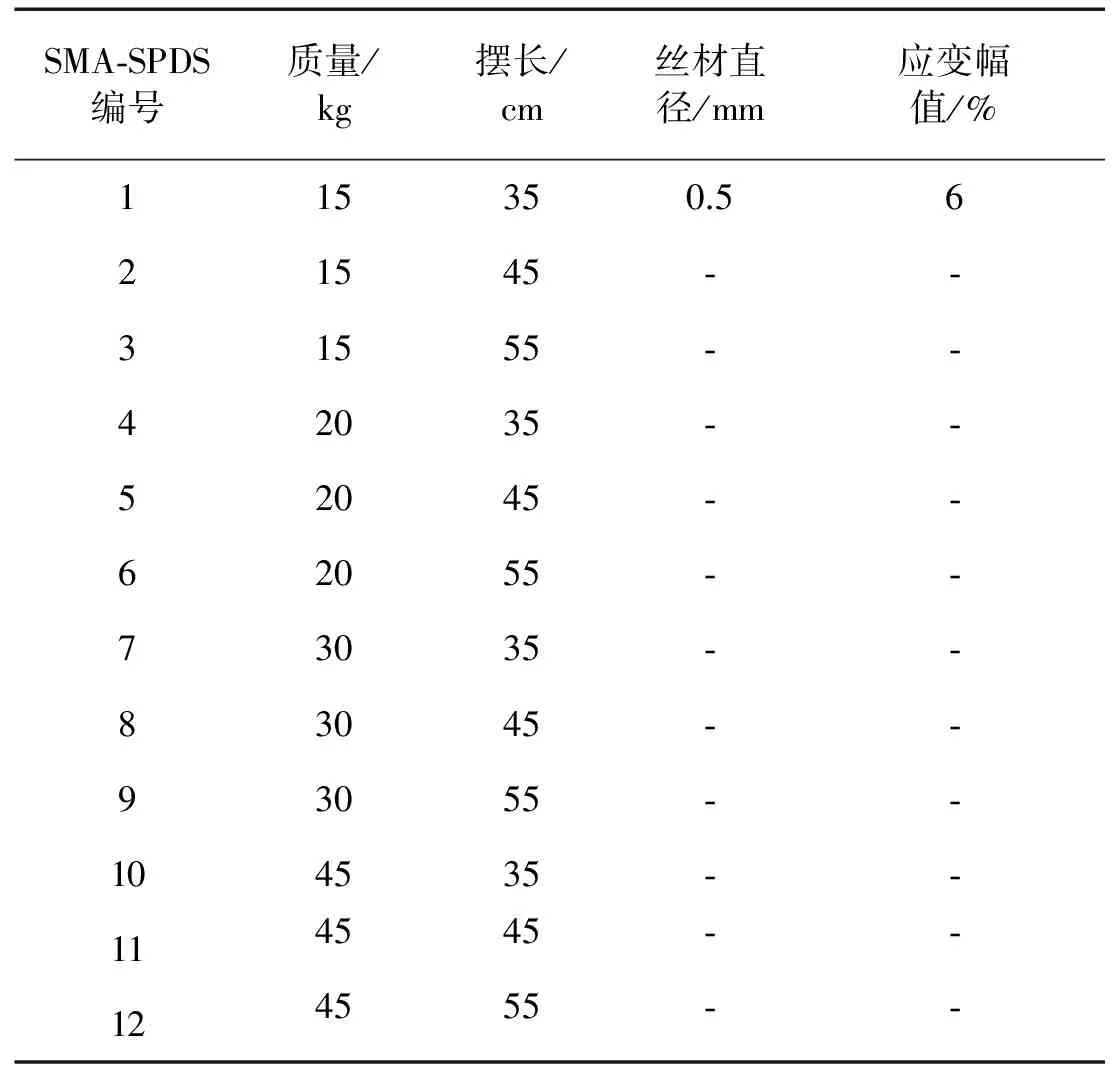
表5 SMA复合悬摆减震系统性能试验工况

图6 SMA复合悬摆减震系统性能试验照片

4.1 频率分析

采用初位移法得到减震系统位移衰退曲线，对其进行相应的FFT频谱分析，即可得到SMA复合悬摆减震系统振动频率，如表6所示。

表6 减震系统的自振频率

由表6可得：所设计的减震系统自振频率集中于0.8 Hz附近；随着摆线长度的增加，频率逐渐下降；同时，随着振子质量的增加，频率逐渐增加。

4.2 相位分析

SMA复合悬摆减震系统能否对受控结构实现所谓的“反共振”，即质量振子是否与受控结构产生“相反”的运动[8]。若出现迟滞或同向运动，则可能没有效果甚至会加剧受控结构的动力响应。为此，必须使所设计的SMA-SPDS中质量振子相对受控结构的位移与台面速度方向完全相反，此时即可获得最优的减震效果[9]。

根据前述所得减震系统自振频率，采用正弦激励下的共振试验法，在减震系统自振频率(0.8 Hz)附近对其进行强迫振动，以分析质量振子相对台面的位移与台面速度方向之间的相位关系。图7为1，2号减震系统的质量振子相对台面位移与台面速度的时程曲线。1～12号减震系统的质量振子与台面相位关系，如表7所示。

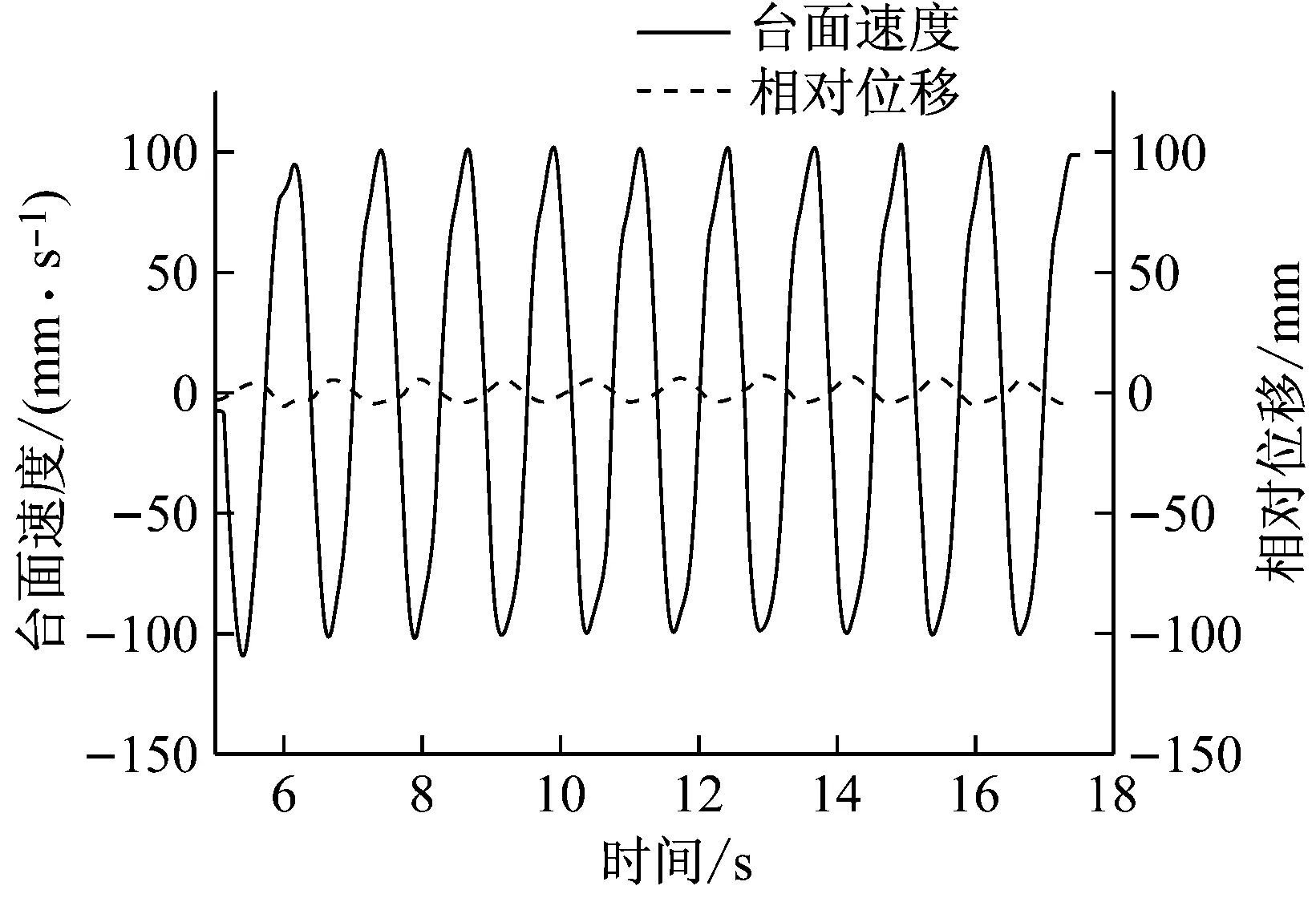
(a) 1号减震系统

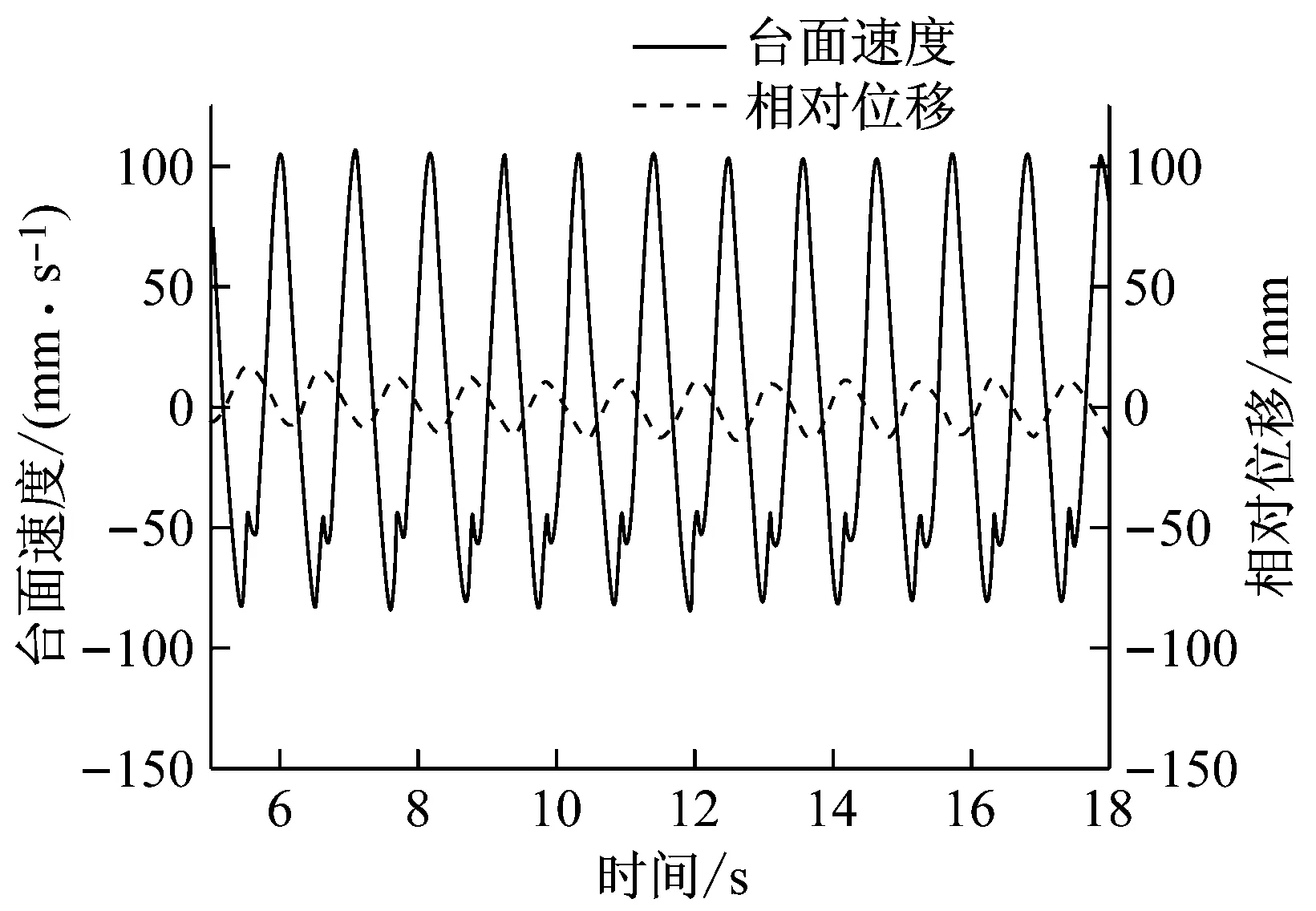
(b) 2号减震系统

根据图7和表7可得：SMA复合悬摆减震系统的质量振子相对台面的位移与台面速度方向之间的相位关系始终保持在在150°～180°之间，即质量振子与台面的运动方向始终“相反”，从而验证了该减震系统的有效性。

表7 SMA复合悬摆减震系统的相位关系

4.3 SMA复合悬摆减震系统等效阻尼力

为描述SMA复合悬摆减震系统的出力性能，定义如下力学参数：将受控结构简化为单自由度体系，在振动荷载F(t)作用下受控系统(原结构)和减震系统的动力学方程分别[10]为

(1)

(2)

式中：Fe(t)即为该减震系统附加给原结构的等效阻尼力。由受控结构和减震系统的相互作用关系，可知等效阻尼力的计算公式

(3)

针对上述12种阻尼器，分别进行正弦、真实地震荷载作用下的SMA复合悬摆减震系统等效阻尼力变化规律的研究。其中正弦荷载作用时，位移幅值分别 为2 mm、4 mm、6 mm、8 mm，加载频率为0.8 Hz；真实地震荷载采用EL-Centro波，加速度分别为100 gal、200 gal、300 gal、400 gal、500 gal。限于篇幅，文中仅列出8号减震系统在正弦荷载(幅值6 mm)及400 galEL-Centro波作用下的等效阻尼力时程曲线，如图8所示。图9为1～12号减震系统分别在正弦、EL-Centro波激励下等效阻尼力幅值的变化规律。

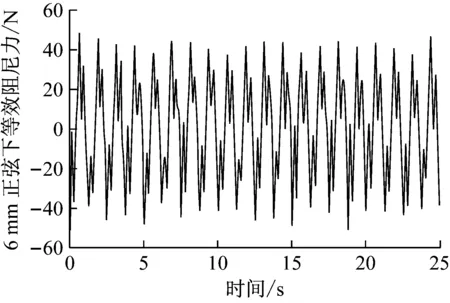
(a) 6 mm正弦荷载作用

(b) 400 gal EL Centro波作用

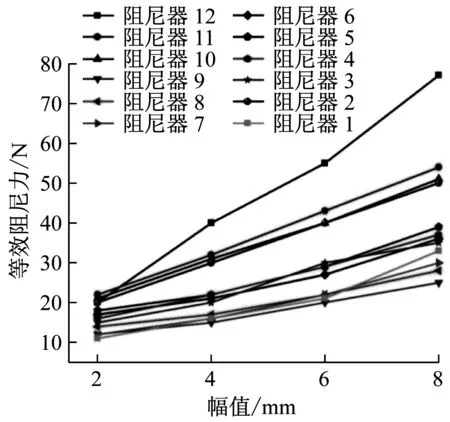
(a) 正弦荷载作用

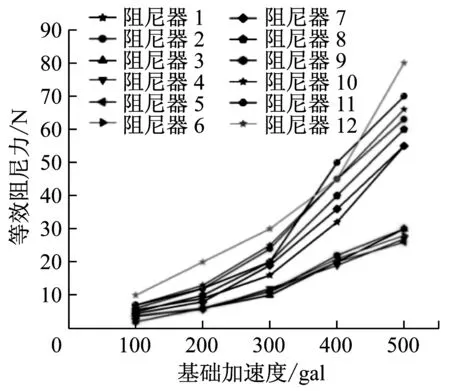
(b) EL Centro波作用

由上述试验结果可得：文中所提出的SMA复合悬摆减震系统具有良好的出力性能，并且等效阻尼力随荷载幅值的增加而增大。其中，振子质量对等效阻尼力有较大的影响，在相同荷载输入下，该减震系统的等效阻尼力随着振子质量增大有明显的提高，最大增幅可达43%，摆杆长度对该减震系统的等效阻尼力影响较小。同时，该套减震系统等效阻尼力随着地震强度的增加，其值亦明显增大，即：SMA复合悬摆减震系统对于结构在较大振动荷载作用下的控制效果更加明显。

5 结 论

本文系统研究了SMA丝随材料直径、应变幅值、加载循环次数变化下的应力-应变曲线、特征点应力、耗能能力、等效阻尼比等变化规律。基于上述规律，选用合适的SMA丝材，经过训练，结合调谐质量阻尼器基本工作原理，设计制作了一类可便于拆卸的SMA复合悬摆减震系统，并对其进行了相关的性能试验，结论如下：

(1) SMA丝各力学性能特征值等随着其直径的增加，均出现不同幅度降低；耗能效率在应变幅值为6%左右时达到最大；随着加载循环次数的增加，各特征点值均有不同程度的降低，但经过15周循环加载后，各特征值趋于稳定。为此，按照上述规律，选用直径为0.5 mm，应变幅值为6%，并预先经过15周循环加载训练的SMA丝材应用于SMA-SPDS系统的开发。

(2) 采用正弦激励下的共振试验法，对SMA复合悬摆减震系统进行相位分析，结果表明，该减震系统中质量振子与受控结构相对位移和台面速度二者之间的相位关系始终保持在150°～180°之间，即：该套减震系统能够实时的为受控结构提供可靠、有效的阻尼力。

(3) 对不同振子质量、不同摆长等12种SMA复合悬摆减震系统进行不同位移幅值下的正弦波和不同强度的EL-Centro波激励，结果表明该减震系统的等效阻尼力随着振子质量增大有明显的提高，最大增幅可达43%，但摆杆长度对减震系统的等效阻尼力影响较小。同时，该套减震系统等效阻尼力随着地震强度的增加，其值亦明显增加，即：SMA复合悬摆减震系统对于结构在较大振动荷载作用下的控制效果更加明显。

[1] 薛素铎，石光磊，庄鹏. SMA复合摩擦阻尼器性能的试验研究[J].地震工程与工程振动，2007(2):145-151.

XUE Suduo, SHI Guanglei, ZHUANG Peng. Performance testing of SMA incorporated friction dampers[J].Journal of Earthquake Engineering and Engineering Vibration,2007(2):145-151.

[2] 孟庆利.SMA金属橡胶阻尼器减振效能试验研究[J].西安建筑科技大学学报(自然科学版)，2015(6):804-807.

MENG Qingli. The study on dissipation behavior of SMA pseudo-rubber metal damper by experiments[J].Journal of Xi’an University of Architecture & Technology(Science and Technology), 2015(6):804-807.

[3] 邢德进.新型SMA阻尼器及结构减震控制应用研究[D].天津：天津大学，2008.

[4] CORBI O. Shape memory alloys and their application in sturctural oscillations attenuation[J]. Simulation Modeling Practice and Theory, 2003, 11(5/6): 387-402.

[5] 陈云，吕西林，蒋欢军.新型耗能增强型SMA阻尼器设计和滞回耗能性能分析[J].中南大学学报(自然科学版)，2013(6):2527-2536.

CHEN Yun, LÜ Xilin, JIANG Huanjun. Design and hysteretic energy analysis of new enhanced energy dissipation SMA damper[J]. Journal of Central South University(Science and Technology), 2013(6):2527-2536.

[6] 任文杰，李宏男，宋钢兵，等.新型自复位SMA阻尼器对框架结构减震控制的研究[J].土木工程学报，2013(6):14-20.

REN Wenjie, LI Hongnan, SONG Gangbing, et al. Study on seismic response control of frame structure using innovative re-centring SMA damper[J].China Civil Engineering Journal, 2013(6):14-20.

[7] 吴昀泽.形状记忆合金的力学性能与本构模型研究[D].广州：华南理工大学,2012.

[8] ANH N D, NGUYEN N X. Design of TMD for damped linear structures using the dual criterion of equivalent linearization method[J]. International Journal of Mechanical Sciences, 2013, 77(12): 164-170.

[9] 覃方芳.被动调谐质量阻尼器用于多层厂房振动控制的研究[D].兰州：兰州理工大学，2012．

[10] CLOUGH R W, PENZIEN J. Dynamics of structures[M]. McGraw-Hill, 2007:15-17.

Tests for performance of Ti-Ni SMA suspension pendulum vibration reduction system

WANG Sheliang1, YU Binshan1, FAN Yujiang2, YANG Tao1

(1. School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China; 2. School of Architecture, Chang’an University, Xi’an710061, China)

The varying laws of stress-strain curve, feature points’ stress, energy-dissipation capacity, and equivalent damping ratio of Ti-Ni shape memory alloy (SMA) wires were studied with the variation of diameter of wires, strain amplitude and loading cyclic number. The results showed that increase in SMA wires’ diameter can degrade the mechanical properties of SMA wires; SMA wires can have good and stable hysteretic performance when the strain amplitude is 6% and the loading cyclic number is 15. Utilizing the super-elastic characteristics of SMA wires obtained with training and combining the operating principle of tuned mass dampers, a kind of SMA suspension pendulum vibration reduction system being easy to disassemble was designed and fabricated. The system’s corresponding performance tests were conducted to analyze the system’s natural frequency, the phase relation between the mass vibrator and the controlled structure, and the varying laws of the equivalent damping force with variation of vibrator mass and swing link length. The results showed that the phase relation between the mass vibrator and the controlled structure can retain well in the range of 150°-180° when this system is subjected to sine waves and real earthquake waves; meanwhile, the control effects of the equivalent damping force can be improved significantly with increase in amplitude of external loads; generally speaking, this system can be applied simply and easily in vibration control of structures to provide a stable and effective damping force and protect structures from strong dynamic disasters.

super-elastic characteristics; SMA suspension pendulum vibration reduction system; phase relation; equivalent damping force

国家自然科学基金(51678480)；陕西省工业攻关项目资助(2014K06-34)；陕西省博士后基金(SX2014120057)

2016-07-18 修改稿收到日期：2016-10-11

王社良 男，教授，1956年11月生

TU502+.6

A

10.13465/j.cnki.jvs.2017.11.007