基于LS-DYNA的扇形中深孔逐孔起爆段别优化
邓红卫, 杨懿全, 高 峰, 周科平, 张 健
(中南大学 资源与安全工程学院, 长沙 410083)
基于LS-DYNA的扇形中深孔逐孔起爆段别优化
邓红卫, 杨懿全, 高 峰, 周科平, 张 健
(中南大学 资源与安全工程学院, 长沙 410083)
梅山铁矿是典型的“城市矿山”,控制爆破振动效应对周边建筑安全意义重大。为优化其微差参数,降低爆破振动效应,利用LS-DYNA建立了准二维扇形中深孔爆破模型,在原典型微差方式的基础上,设计了五种不同段别组合的逐孔起爆方案,识别了各孔段振动速度波形,比较了各方案各孔段波形峰值。结果表明:间隔一至两个段别的微差方式更有利于应力波干涉减震;对于多孔段逐孔爆破,统一地改变孔间间隔时间往往不达到整体减震的目的;对于梅山铁矿的爆破参数,起爆段别调整为1-3-4-5-6-8-9-10-11段更有利于爆破振动效应的控制。针对模拟得出的最优方案进行了现场对比验证,现场试验表明:相对于原方案,优化后方案井下减震11.4%,地表减震15.2%,说明优化方案具有一定的应用价值。
爆破振动; 扇形中深孔; 多孔段波形; 段别组合; LS-DYNA
井下中深孔采矿爆破药量大,其振动效应也往往较大。梅山铁矿采用无底柱分段崩落法落矿,一次爆破药量超过1 t,距离南京市区仅12 km,随着南京城市建设的不断向外扩展,已逐渐成为了“城市矿山”,居民区与回采爆破区域最近水平距离300~400 m,针对该矿山的爆破振动效应控制显得尤为重要。目前矿山基本上采用逐孔起爆技术,降低了最大单段药量,因而合理优化其孔间微差时间是震源处减震方法中为数不多的有效途径。
目前,关于微差时间的理论研究与计算方法众说纷纭,大体上可分为自由面原理、应力波叠加原理、增强碰撞作用原理、地震波干扰降震原理等,但爆破过程的复杂性和作用机理的综合性使得最优微差时间尚未有一个明确的定论。国内外学者基于上述理论、利用单孔波形、时频分析、能量分析、数值模拟、现场试验等方法做了大量的研究,其中崔正荣等[1]利用基于VB6.0平台建模进行波形叠加,得到使得爆破振动速度最小的微差时间为23 ms;史秀志等[2]对不同微差时间爆破地震波进行时频特性分析,得出较优的微差间隔时间为30 ms、40 ms;叶海旺等[3]利用小波分析技术,从能量的角度探索了适合金堆城露天矿生产爆破的合理微差时间为孔间42 ms,排间100 ms;张大宁[4]运用LS-DYNA程序建立二维双孔模型,对大孤铁矿合理微差时间进行了研究,得出使用高精度非电导爆管雷管的最优微差时间为孔间25 ms和排间65 ms,使用数码电子雷管,则分别为35 ms和70 ms;张袁娟等[5]结合LS-DYNA与MATLAB程序分析了不同微差时间下的爆炸模型的振动速度与能量的衰减规律,得出了最优微差时间为42 ms;吴贤振等[6]利用LS-DYNA程序计算了不同为微差时间下的采空区顶板振动速度,结果表明7 ms/s的间隔时间干涉减震效果最优;严加刚[7]对西石门铁矿扇形中深孔微差爆破进行了现场试验;占时春等[8]对兰尖铁矿进行了孔内孔间微差爆破技术的试验研究。
由于地质条件和爆破参数的变异性,最优微差时间的结论也存在较大差距,同时爆破振动效应受众多因素影响[9-11],从单一理论出发计算微差时间也具有一定的局限性,而通过数值计算可直接反映微差爆破过程,简便经济。但目前的数值模拟往往是通过双孔模型验证单一的最优微差时间,对于多孔多段扇形中深孔的段别组合的研究较少。本文利用LS-DYNA程序建立准二维排面模型,设计不同段别组合,通过识别各孔段振动速度波形并比较其峰值,验证其干扰减震的整体效果。
1 数值模型的建立
1.1 梅山铁矿爆破参数
梅山铁矿回采用上向扇形中深孔,扇形倾角为90°,边孔角为60°,孔底距为2.5~3.2 m,单孔孔深为13~25 m,孔径90 mm,崩落排距2.4 m,每排9~10孔,炸药单耗为0.25~0.35 kg/t,装药密度为6.5 kg/m,装药系数0.8。使用奥瑞凯非电雷管,各段别微差间隔时间为25 ms,起爆药包布置在孔底,直接引爆主爆药。扇形孔布置见图1。
1.2 LS-DYNA模型的建立
根据回采爆破参数在LS-DYNA中建立由炸药、矿石、覆岩组成等比例准二维模型,模型采用六面体单元,流固耦合算法,在炮孔周围建立一层空体积网格,与炸药网格耦合,炸药网格与矿石网格耦合,空体积与矿石网格重合,定义炸药、空体积组成的ALE网格与矿石、围岩组成的Lagrange网格流固耦合。计算单位制为cm-g-us。模型见图2。

图1 扇形中深孔布置剖面图

图2 有限元单元网格图
为描述无限岩体的情形,在模型四周施加无反射边界,采矿进路为自由边界,准二面施加对称约束。
1.3 材料参数
1.3.1 矿岩参数
梅山铁矿矿体赋存于花岗岩中,岩体材料选用塑性随动模型(MAT_PLASTIC_KINEMATIC)。主要物理参数见表1。
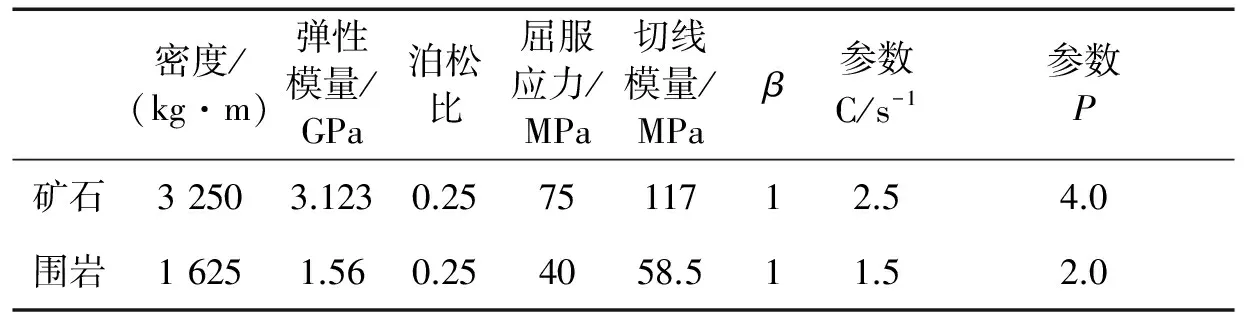
表1 矿岩主要物理力学参数
1.3.2 炸药参数
梅山铁矿采用粒状铵油炸药,选用高能炸药模型(MAT HIGH EXPLOSIVE BURN),结合描述爆轰产物压力-体积JWL状态方程计算爆轰过程中的压力。JWL状态方程如下:
(1)
式中:p为压力;V为相对体积;E0为初始内能密度;A,B,R1,R2,ω为试验确定的常数。

表2 炸药参数
2 模拟过程与结果
2.1 原典型方案
目前,梅山铁矿典型微差方式主要分两大段,即中心三孔起掏槽作用为第一大段,周边孔为第二大段,两大段起爆时间相隔300 ms,间隔时间较长,具体段别为1-2-3-15-16-17-18-19-20,每段间隔25 ms,见图3。

图3 现用典型微差方案
一方面,较长的时间间隔会减小两段波的在爆破近区的叠加,另一方面时间间隔长也意味着爆破振动时间的增加,对于应力波的叠加可至弱也可至强,受诸多因素影响,较难通过理论方法精确计算,故原方案微差方式存在一定的优化空间。可通过设计各段不同段别组合,进行数值模拟,对比分析,比较确定最佳微差方式。
2.2 孔段波形的确定
孔段波形指的是各孔爆炸引发的某质点振动合速度时程曲线波形。在实际过程中,由于多段爆炸的干扰叠加和传播过程中的反射、折射等,难以从监测到的振动合速度提取分解出孔段波形,但近爆区振动速度波形特性受地质影响干扰较小,微差间隔也较为明显,往往能反应孔段波形。但若监测点距离炮孔太近,其受最近的单个炮孔爆炸应力波影响较大,波形局部特征明显。为反映波形的整体情况,选取模型边角上的两节点,即采矿进路底板右7 m、高1 m处节点和围岩内对称节点作为监测点,监测其振动合速度。
对典型方案进行数值计算发现,由于围岩的弹性模量等物理力学参数较矿岩弱,且监测到的应力波在传播过程需经过介质界面,发生了较多的反射、折射,振动特性较为复杂,振动速度峰值多而杂,已无法辨别孔段波形。

图4 监测点位置

图5 典型方案不同监测点振动速度
矿岩内节点振动速度曲线波峰离散而清晰,其出现时间也与微差控制时间较为吻合,这是由于矿岩为炸药爆炸直接介质,质点振动速度曲线特性受各单孔爆炸应力波影响,规律性强,孔段波形较为显著,可结合微差间隔与应力波传播时间,判断各波形对应的段别,进而分析比较其振动叠加情况:第一、二个波峰即对应第一二段别,而第三段爆破炮孔处于监测点另一侧,波形峰值出现时间应较第一二次波峰间隔时间较长,故第三段别对应时间上更为符合的第四个波峰,第三个波峰实质为前两段爆破的应力反射波所致,第十五段别对应波形出现350 ms以后,即五个波峰,第十六段爆破炮孔位于监测点异侧,第六个波峰在出现时间上满足要求,故十六段别即对应第六个波峰,同理,可依次确定各个段别对应的波峰。

图6 典型方案的各孔段波形曲线
2.3 微差优化方案
由于原典型方案两大段起爆时差为300 ms,间隔时间较长,可以考虑缩短两大段爆破时间间隔,设计方案一、二;由于首段爆破药量最大,引发的孔段波形峰值高,可考虑延长下一段的延迟时间,改变首段与后段爆炸应力波叠加,设计方案三;由于国内矿山爆破间隔时间一般为每米最小抵抗线取15~25 ms[12],由此,原方案孔间延时间隔25 ms较短,可考虑增加逐孔间隔时间,设计方案四;继承原方案分大段减震的思想,增加为3大段,设计方案五,如表3所示。

表3 设计方案
2.4 计算结果
各方案计算结果如下:
统计各方案各段别振动速度波形峰值,如表4所示。
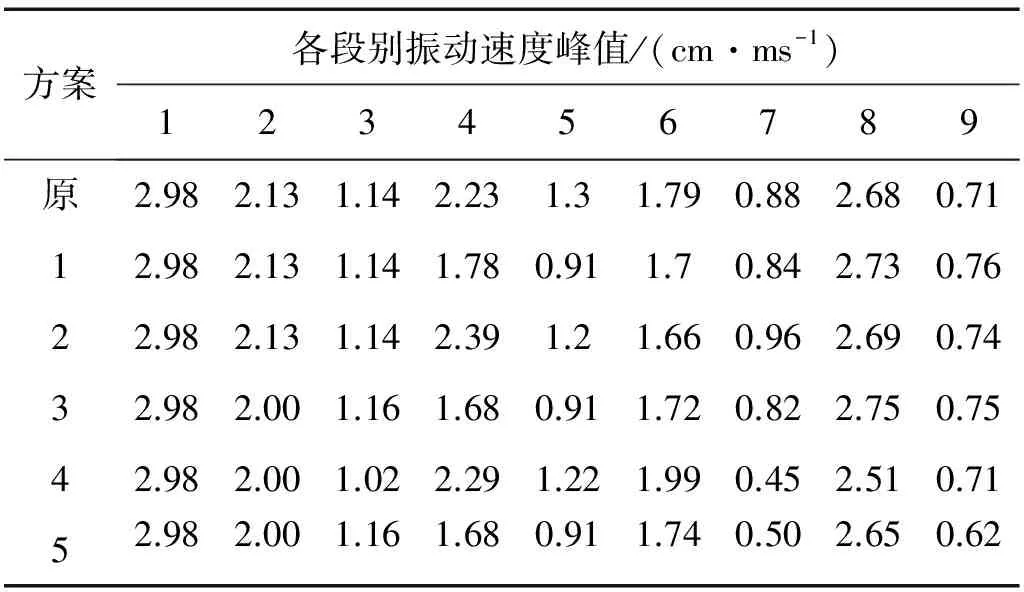
表4 各方案各段别振动速度峰值
2.5 对比分析
(1) 缩短两大段间隔时间
对比原典型方案、方案一、方案二发现,将第3次序孔爆破与第4次序孔爆破间隔时间缩短后,各孔段波形峰值改变最明显的是4,5次序孔。当间隔时间减小为50 ms时,第4次序孔波形峰值增大,而第5次序孔波形峰值略有减小,当间隔时间减小为25 ms时,第4,5次序孔波形峰值分别从2.23 cm/ms和1.3 cm/ms减小为1.78 cm/ms和0.91 cm/ms,减振率达20%~30%。这是由于随着爆破间隔时间的缩短,前三孔爆破应力波与第四、五孔应力波发生叠加干扰发生变化,当间隔时间为50 ms时,叠加增强,间隔25 ms时,叠加减弱。综上所述,缩短两大段别微差时间25 ms,更有利于应力波干扰减震。
(2) 增加首段与下一段间隔时间

(a) 方案一

(b) 方案二

(c) 方案三

(d) 方案四
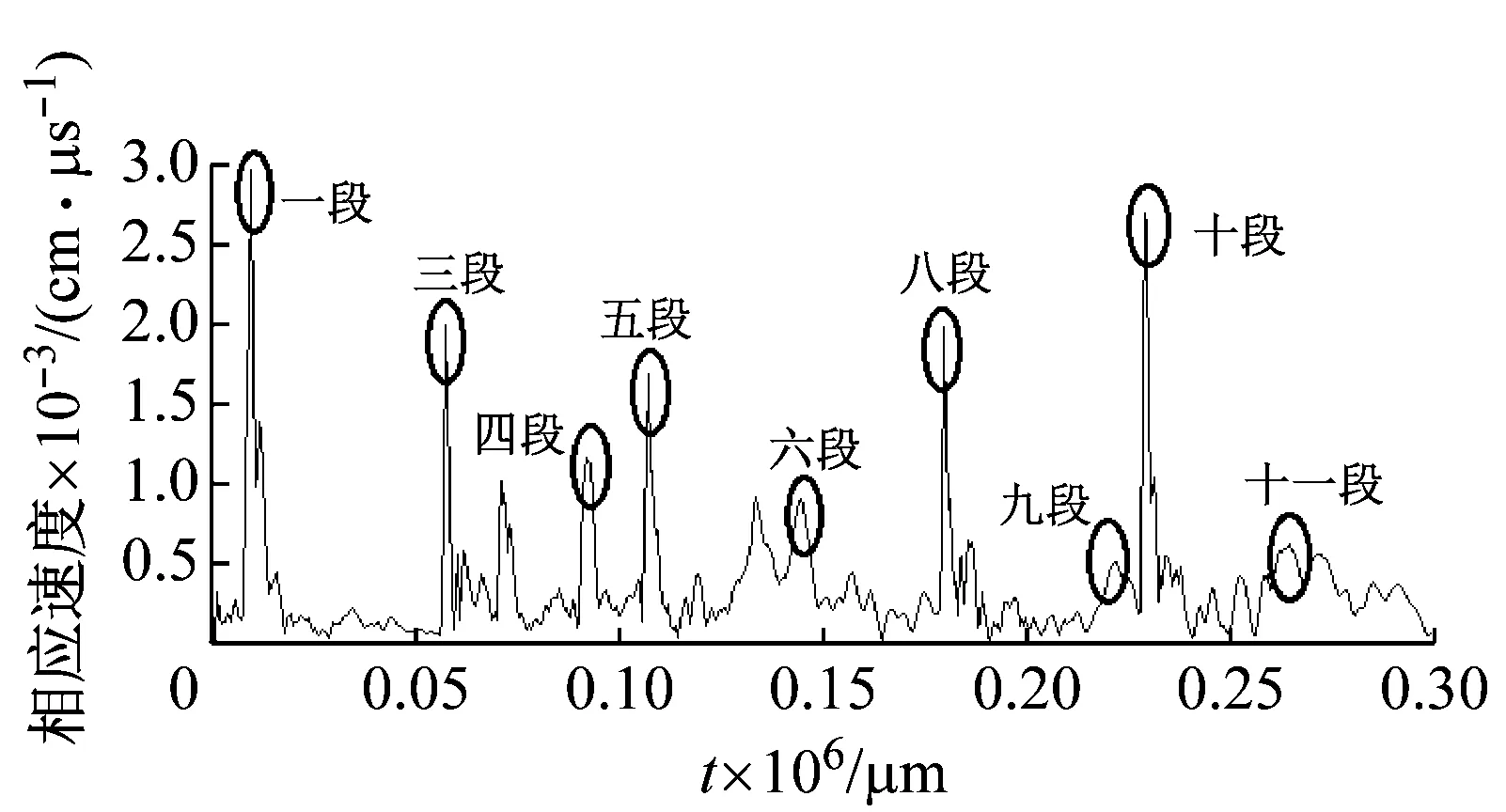
(e) 方案五
对比方案一与方案三发现,当增加首段与下一段间隔时间至50 ms时,对第2,4次序孔振动速度略微减小,说明间隔50 ms使得第一、二孔爆破振动应力波叠加干扰程度大于间隔25 ms的情形,故第一二次序孔间隔50 ms更有利于爆破振动的控制。
(3) 增加逐孔间隔时间

图8 两大段不同间隔时间的孔段波形峰值

图9 首后段不同间隔时间的孔段波形峰值
对比方案一与方案四发现,将所有孔间隔时间从25 ms增加到50 ms,各孔段波形峰值变化具有周期性,其中2,3次序孔振动减弱,4,5,6次序孔振动加强,7,8次序孔振动再减弱,这说明改变逐孔间隔时间使得各孔段应力波叠加发生整体改变,某孔段的波形叠加后减弱往往会导致下孔段的波形叠加增强,在多孔段爆破中,单一改变逐孔微差时间,往往达不到整体干扰降震的目的。

图10 不同逐孔间隔时间的孔段波形峰值
(4) 增加微差大段数
对比方案三与方案五发现,增加大段数量为3段,即延长第5次序孔与第6次序孔间隔时间至50 ms后,第6次序孔波形峰值从1.72 cm/ms略微增加至1.74 cm/ms,但第7,8,9序列孔波形峰值从0.83 cm/ms、2.75 cm/ms、0.75 cm/ms减小至0.50 cm/ms、2.65 cm/ms、0.62 cm/ms,应力波叠加减弱较大,说明增加第5,6次序孔爆破间隔时间50 ms能有效增加爆破应力波的叠加干扰,减小爆破振动效应。

图11 增加微差大段数量的孔段波形峰值
综上所述,原微差段别方案1-2-3-15-16-17-18-19-20中,第3次序孔与第4次序孔间隔时间较长,不利于应力波的叠加干扰,爆破振动效应较大,间隔时间缩短至25 ms,则能有效增加应力波干扰,减小爆破振动;由于多孔段爆破应力波叠加的复杂性,单纯改变逐孔间隔时间往往难以达到整体降震的目的;首段药量较大,延长后段的间隔时间为50 ms,有利于爆破减震,将5,6次序孔间隔时间延长为50 ms,增加大段数量,更有利于爆破振动效应的控制。模拟结果表明,1-3-4-5-6-8-9-10-11的三大段微差方式干扰减震效果最好。
对于干扰减震,一般认为前后段别微差时间确定为单孔波形半个周期奇数倍能达到最好的减震效果,但实际作用过程往往是多段叠加干扰,且受到孔网布置、地质结构、传播距离等因素的影响,情况更为复杂。较理想的设计思路是使得相邻段别主震相在时间轴上相互分离[13]。主震相持续时间与药量正关联,且存在一定的积累延长效应,模拟最优方案遵循上述原则,较好地错开了各段主震相。
3 现场试验
3.1 现场试验方案与地点
为验证模拟得出的最优方案的减震效果,选取爆破振动效应最为显著的西北区作为试验区域,采用井下和地面联合监测的方式,使用TC-4850爆破测振仪监测-318分段5-6L N17连续两个排面的回采爆破。两排面爆破除微差方式外,其余爆破参数相同。
试验对比方案,如表5所示。

表5 现场试验对比方案
具体爆点测点位置见图12。
3.2 现场试验结果
试验结果如表6所示。

表6 现场试验数据

图12 现场试验位置图

从表6可知,试验方案的地表和地下振动效应均小于原方案,其中井下振动合速度从4.350 cm/s减小到3.852 cm/s,减震率为11.4%,地表从0.302 cm/s减小到0.256,减震率为15.2%。说明改进后的方案具有一定的减震效果。
值得注意的是,相比原方案,试验方案爆破后的大块率有所增加,这是由于试验方案缩短了中心掏槽孔与两侧炮孔的微差时间,掏槽后自由面可能未充分形成,从而影响了爆破效果。
4 结 论
利用LS-DYNA建立了准二维扇形中深孔排面模型,分析梅山铁矿目前的典型微差方案,从缩短两大段间隔时间、增加首段与下段间隔时间、增加逐孔间隔时间、增加微差大段数量四个方面出发,设计了五种不同的段别组合方案,监测采矿进路侧壁内节点的振动合速度,分析了各方案振动速度时程曲线特征,依据微差时间和应力波传播时间确定各孔段对应的振动速度波形,通过比较各方案的波形峰值,确定了最优方案,并进行了现场对比试验。具体结论如下:
(1) 各孔微差时间不宜过长,孔间微差一至两个段别的微差方式更有利于应力波的叠加干涉,减小爆破振动。
(2) 对于多孔段逐孔爆破,统一地改变孔间间隔时间往往不达到整体减震的目的。
(3) 逐孔爆破前后孔段应力波叠加复杂,最优段别组合的确定是个循序渐进的过程。根据模拟结果,对于梅山铁矿的爆破参数,1-3-4-5-6-8-9-10-11的三大段微差方式干扰减震效果最好。
(4) 对最优方案进行了现场对比试验,相对于原方案井下减震11.4%,地表减震15.2%,但爆破后大块率有所增加。说明模拟的最优方案虽然爆破效果略有欠缺,但存在较好的减震效果,在距离保护区域较近的采区仍具有一定实际意义。
[1] 崔正荣,张西良.梅山铁矿深孔爆破合理微差时间研究[J].现代矿业,2014,5(5):9-39.
CUI Zhengrong,ZHANG Xiliang.Research on reasonable different time of deep hole blasting in Meishan iron mine[J].Modern Mining,2014,5(5):9-39.
[2] 史秀志,陈寿如.爆破振动信号时频特征的微差时间效应[J].湖南科技大学学报(自然科学版),2008,23(3):10-13.
SHI Xiuzhi,CHEN Shouru.Delay time interval effect for time-frequency characteristic of blasting vibration signal[J].Journal of Hunan University of Science & Technology(Natual Science Edition),2008,23(3):10-13.
[3] 叶海旺,石文杰,王二猛,等.金堆城露天矿生产爆破合理微差时间的探讨[J].爆破,2010,27(1):96-98.
YE Haiwang,SHI Wenjie,WANG Ermeng,et al.Research of reasonable delay intervals in Jinduicheng open-pit mine[J].Blasting,2010,27(1):96-98.
[4] 张大宁.大孤山铁矿微差爆破延期时间的优化研究[J].矿业研究与开发,2010,30(4):88-89.
ZHANG Daning.Delay time interval optimization of double holes millisecond blasting in Dagushan iron mine[J].Mining R&D,2010,30(4):88-89.
[5] 张袁娟,黄金香,农冬灵,等.某露天矿生产爆破合理微差时间探讨[J].煤炭技术,2013,32(12):201-203.
ZHANG Yuanjuan,HUANG Jinxiang,NONG Dongling, et al.Stusy on reasonable millsecond delay time in ope-pit mine[J].Coal Technology,2013,32(12):201-203.
[6] 吴贤振,尹丽冰,刘建伟,等.基于LS-DYNA的临近采空区多段爆破微差时间优化研究[J].爆破,2015,32(1):87-92.
WU Xianzhen,YIN Libing,LIU Jianwei,et al.Optimization of blasting delay time near underground goaf based on LS-DYNA[J].Blasting,2015,32(1):87-92.
[7] 严加刚.扇形中深孔孔间微差爆破在西石门铁矿的应用[J].矿业研究与开发,2003,23(5):53-54.
YAN Jiagang.Application of fan middle deep-hole millisecond blasting in Xishimen iron mine[J].Mining R&D,2003,23(5):53-54.
[8] 占时春,李山存.孔内孔间微差爆破试验研究[J].工程爆破,2006,12(2):53-54.
ZHAN Shichun,LI Shancun.Experimental study on millisecond blasing both in and among holes[J].Engineering Blasting,2006,12(2):53-54.
[9] 陈士海,燕永峰,戚桂峰,等.微差爆破降震效果影响因素分析[J].岩土力学,2011,32(10):3003-3008.
CHEN Shihai,YAN Yongfeng,QI Guifeng,et al.Analysis of influence factors of interference vibration reduction of millisecond blasting[J].Rock and Solid Mechanics,2011,32(10):3003-3008.
[10] 张青成,王家磊,李德璇,等.露天矿山爆破振动影响因素分析研究[J].辽宁工程技术大学学报(自然科学版),2013,32(10):1334-1338.
ZHANG Qingcheng,WANG Jialei,LI Dexuan,et al.Grey correlation method in application of influence fators analysis of open-pit mine blasting vibration[J].Journal of Liaoning Technology University(Natural Science),2013,32(10):1334-1338.
[11] 杨珊,陈建宏,郭宏斌,等.隧道爆破振动影响因素的灰色关联分析[J].中国安全科学学报,2011,21(6):65-71.
YANG Shan,CHEN Jianhong,GUO Hongbin,et al.Grey relation analysis of influence factors of tunnel blasting vibration[J].China Safety Science Journal,2011,21(6):65-71.
[12] 林大泽.降低地下矿深孔爆破落矿大块率的技术措施[J].中国安全科学学报,2007,17(1):86-90.
LIN Daze.Technical measures on lowering boulder yield during deep-hole blasting in underground mine[J].China Safety Science Journal,2007,17(1):86-90.
[13] 郭学彬,张继春,刘泉,等.微差爆破的波形叠加分析[J].爆破,2006,23(2):4-8.
GUO Xuebin,ZHANG Jichun,LIU Quan,et al. Analysis of waveform superimposed action of millisecond blasting[J].Blasting,2006,23(2):4-8.
Optimization of millisecond parameters for hole by hole initiation in fan-shape deep holes based on LS-DYNA
DENG Hongwei, YANG Yiquan, GAO Feng, ZHOU Keping, ZHANG Jian
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Meishan iron mine is a typical “urban mine”, it is very important to control its blasting vibration effects to ensure the safety of surrounding buildings. In order to optimize millisecond parameters and reduce blasting vibration effects, a blasting model for quasi two-dimensional fan-shape deep holes was built with LS-DYNA. On the basis of the current typical millisecond blasting parameters, five different millisecond patterns for hole by hole initiation were designed, the vibration velocity waveform of each hole in different patterns were identified, and their peaks were compared. Results showed that the reasonable blasting delay time of each hole should be 25ms~50ms to reduce blasting vibrations due to stress wave interference; for multi-hole hole by hole initiation, the whole vibration reduction can’t be achieved only with uniformly changing blasting delay time of each hole; for blasting parameters of Meishan iron mine, the detonator group 1-3-4-5-6-8-9-10-11 is more appropriate to control blasting vibration effects. Besides, field comparative test was conducted, the results showed that compared with the original blasting scheme, blasting vibrations caused with the optimized pattern 5 are reduced by 11.4% underground and 15.2% on surface, so the optimized pattern has a certain applicable value.
blasting vibration; fan-shape deep holes; multi-hole blasting waveform; millisecond parameters; LS-DYNA
国家自然科学基金(51204205)
2015-12-03 修改稿收到日期:2016-04-23
邓红卫 男,博士,副教授,1969年生
杨懿全 男,硕士生,1991年生
TD235.4
A
10.13465/j.cnki.jvs.2017.11.022

