滑动轴承摩擦故障趋势预测的系统自记忆模型

张峻宁， 张培林， 华春蓉， 吴定海

(1.军械工程学院 七系，石家庄 050003；2.西南交通大学 机械工程学院，成都 610031)

滑动轴承摩擦故障趋势预测的系统自记忆模型

张峻宁1， 张培林1， 华春蓉2， 吴定海1

(1.军械工程学院 七系，石家庄 050003；2.西南交通大学 机械工程学院，成都 610031)

针对滑动轴承时间序列非线性引起的接触摩擦故障趋势难预测的问题，提出一种基于系统自记忆预测模型的滑动轴承接触摩擦故障趋势预测方法。该方法首先根据信号激励源不同的特点，将采集信号分离为冲击声和随机声，然后采用函数拟合、求导和灰色理论分别反演出冲击声和随机声的系统微分方程，并运用双向差分求取不同微分方程对轴承接触摩擦故障信号系统动力核的影响系数。通过引入自记忆函数，将滑动轴承摩擦故障系统动力核反演成一个微分-差分方程，由此得到滑动轴承的自记忆预测模型。应用到静载荷和动载荷的滑动轴承接触摩擦故障实例中，验证了所提方法的有效性，为滑动轴承磨损退化趋势预测提供了一种新的途径。

滑动轴承；摩擦故障；发展趋势；非线性动力系统；信号分离；自记忆模型

滑动轴承是旋转机械(如柴油机)的重要支撑部件，准确预测轴承退化趋势对预防设备性能退化及失效意义重大。但是滑动轴承是一个不断发展变化，密闭的非线性动力学系统，采集的时序资料，规律性差、信息分散，信号激励源复杂，而常用的预测方法[1-5]是基于监测的轴承时序资料，通过建立各类时序预测模型预测故障发展。这些方法均是含参数模型，参数物理意义不明显，有效监测信息缺失。因此，针对滑动轴承时间序列非线性引起的接触摩擦故障，利用上述方法预测效果不佳。近年来，基于动力学不可逆的自记忆预测模型[6-7]得到了发展，广泛应用于气象、环境，经济等领域[8]。自记忆预测模型通过引入包含历史数据的记忆函数，将动力学原理和历史数据联合估计模型参数，是预测科学中确定论和随机论融合在数学上的表现。因此，针对滑动轴承时间序列非线性引起的接触摩擦故障趋势难预测的问题，本文将轴承接触摩擦故障随时间的变化视为动力学系统的非线性时间演化问题，应用自记忆原理预测轴承摩擦故障的发展趋势。在自记忆模型中，为了求解能够描述轴承接触摩擦故障非线性发展的动力核，本文从不同激励源激发轴承不同特点的信号出发，分析信号与激励源的周期性和随机性，尝试分离出对应的信号，利用曲线拟合、求导和灰色理论方法建立反应周期性和随机性特点的动力学微分方程，通过双向差分原则确定其在轴承摩擦故障系统动力核中的影响系数，最终提出一种适合预测滑动轴承接触摩擦故障发展趋势的自记忆模型，实例分析表明，所提方法能较好预测轴承摩擦故障的发展趋势。

1 轴承摩擦故障的动力学模型反演

1.1 轴承摩擦故障的动力学模型识别

由于滑动轴承摩擦系统演化机制复杂，目前还很难基于物理、力学的概念建立描述滑动轴承摩擦非线性演化的微分方程，本文借鉴数据的机理模型识别方法，将滑动轴承的接触摩擦故障变化视为动力学系统的演化问题。本文首先选取声发射(Acoustic Emission, AE)信号均方根值作为滑动轴承接触摩擦故障的监测序列[9-10]，该特征参数对摩擦状态敏感，响应时间快，频率范围宽，信息量大，且计算简单。再根据信号激励源不同的特点，将信号分离为周期声和随机声，然后将滑动轴承周期声和随机声信号的均方根序列视为描述滑动轴承摩擦非线性动力学模型的特解因式，反演出滑动轴承摩擦故障演化的非线性动力学模型。

设有一组描述滑动轴承摩擦故障的AE信号均方根序列：

(1)

作为一种新的滑动轴承AE信号特征序列的分析建模方法尝试，本文采用的滑动轴承摩擦演化的动力学模型的形式为

(2)

式中：x(1)是对滑动轴承AE信号均方根x累加后的变量，f1(z,λ,t)、f2(y,λ,t)是随机信号、周期信号的系统动力核，F(x,λ,t)是滑动轴承摩擦AE信号的动力核，a,β,δ分别为各项动力核的待定系数。当然，按照数据机理建模理论[11]，建模时应在式(2)中置入数据序列隐含的物理项。如序列有明显的周期性，则需要加入正弦、余弦项，序列增长显著应加入指数项。

1.2 信号分离

虽然轴承系统复杂，采集的AE信号干扰因素影响多，但是从统计学角度讲，不同激励源激发的信号可归类为周期性信号和随机性信号。以柴油机输出端主轴承为例，声发射传感器置于附近机体壁上，采集的AE信号主要由柴油机主轴颈的垂向运动惯性力和横向撞击力、进排气阀冲击力、自身轴瓦间的摩擦力等诱发[12]，可大致划分为两类信号，① 冲击声：由冲击性载荷引起的轴承座及设备弹性振动引起的弹性波，具有周期性；② 随机声：轴承出现接触磨损时，动态变化的轴瓦摩擦力激发轴承机座、以及金属表面磨损脱落等引发的AE信号，呈现随机性。对轴承信号的具体划分，如图1所示。

图1 轴承信号的划分

为了将冲击声和随机声分离，利用随机声随机性强的特点，借鉴信号中普通噪声降噪的方法，首先利用K均值奇异值分解(K-means Singular Value Decomposition，K-SVD)字典算法[13]，分离出包含工作脉冲特征的信号(冲击声)，然后再从原始信号中减去冲击声，便得到类似噪声的随机信号(随机声)。图2是对西南交通大学机械实验室柴油机主轴承的信号分离结果(具体实验见3.1节应用实例)。可以发现，图2(b)信号中的冲击成分明显，各脉冲的间隔大约为0.01 s，而柴油机发火燃烧循环所用的时间(T=60/750=0.08 s)，正好与曲轴转角在0°,90°,180°,…,630°时的主轴颈垂向运动惯性力较大值对应，符合柴油机滑动轴承冲击声的定义；图2(c)中信号虽然还含有残余的冲击声信号，但毕竟随机声占主体，利用游程检验检验信号随机性，可知在显著性水平α=0.2(双侧)下接受所检验的数据的序列是随机的，因此可认为是随机声。

设X(0)为归一化后的信号均方根值序列：

(3)

利用式(3)归一化3.2节实例中轴承全部冲击声和随机声，得到轴承从正常到接触摩擦故障的均方根值序列，见图3所示。其中前30 min为轴承摩擦故障早期，30～63 min为轴承严重摩擦故障时期。

分析图3可以发现，冲击声早期平稳后期直线型增长的趋势发展，体现的是冲击力对轴承的冲击反应，由于在轴承摩擦故障初期，轴瓦间存在的残余润滑油，减弱了冲击力激发声波的强度，使其维持在较低水平；严重摩擦故障时(润滑油枯竭)，轴瓦形成干摩擦，缓冲作用较小，脉冲强度呈现直线式递增。随机声则更多的体现的轴瓦摩擦力的变化，“S”型曲线的变化，表明了轴瓦摩擦力是往复逐渐波动，轴与瓦间的摩擦是间歇式的，从初期轴瓦点对点式的接触再到点对面式的接触，最后发展成为面对面式的严重接触，正好符合摩擦学理论。因此，本文将复杂的信号分离为规律相对简单的信号，再反演轴承摩擦故障动力核的思路，更容易捕捉曲线规律。

(a) 轴承接触摩擦故障时AE信号

(b) 冲击声

(c) 随机声

图3 轴承摩擦故障时冲击声和随机声的均方根值变化

1.3 轴承磨损动态预测的反导微分方程

根据分离信号的特点建立描述轴承信号的反演动力学微分方程。

在轴承摩擦故障过程中，由动态变化的摩擦力诱发的随机声信号，随机性强、规律性差，建立轴瓦摩擦反演模型十分困难。灰色模型GM(1,1)凭借数据累加(I-AGO)，将本来数据规律不明显的一组原始数据变得明显的规律，淡化了随机因素，提高了数据内在规律，为此，利用GM(1,1)模型，将数据序列变换为一个变量具有微分、差分和近似指数规律增长的灰色曲线，假设原始数据为

(4)

将该序列进行累加变换后：

(5)

易见，经过一次累加的序列Z(1)，随机性减弱且呈现出指数增大的趋势，以式(5)建立的微分方程

(6)

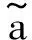
(7)

本文利用GM(1,1)的一阶微分方程式(6)描述随机声曲线的趋势变化，反导出随机声的系统微分方程

(8)

式中：f1(z,λ,r,t)是随机声系统动力核；z是随机声均方根变量;λ为参数；r为空间；t为时间；若考虑固定空间r，随机声系统动力核可简写为f1(z,λ,t)。

因此，随机声系统微分方程的计算，依靠灰色相关理论，在系统信息匮乏、信号序列随机性强的条件下得到解决。

对于轴承冲击声系统的反演微分方程求解，利用式(5)得到累加的冲击声均方根序列Y(1)，视为系统函数f2(y,λ,t)在ti的离散值。其次，由于冲击载荷稳定，随机性较弱的良好特点，假定冲击声均方根曲线大致沿着某一趋势发展，通过曲线拟合得到曲线函数关系

(9)

式中：m为曲线拟合次数；ai是各项系数。

并将冲击声均方根序列Y(i)(1)视为系统函数f2(y,λ,ti)在ti的离散值，即：

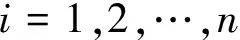
(10)

得到拟合函数与冲击声信号系统微分方程关系

(11)

式中：f2(y,λ,t)是系统动力核；y是变量；λ为参数；t为时间。由此，得到了轴承中冲击声和随机声的反演微分方程。

1.4 摩擦故障演化的动力学模型系数确定

假设信号序列为等间距监测，设Δt=ti+1-ti=1，则可将式(3)轴承动力核方程改写为差分方程：

(12)

又因差分可被表示为向前差分和向后差分，则式(12)表达为

Δxi=xi-xi-1=αf1(z,λ,t)+βf2(y,λ,t)+δ(f1(z,λ,t)f2(y,λ,t))+εbi

(13)

Δxi=xi+1-xi=αf1(z,λ,t)+βf2(y,λ,t)+δ(f1(z,λ,t)f2(y,λ,t))+εfi

(14)

式中：εbi,εfi分别为向前和向后差分误差；方程中α,β,δ系数可通过最小二乘法对极小差分误差函数计算获得

(15)

εbi=(xi-xi-1)-(αf1(z,λ,t)+βf2(y,λ,t)+δ(f1(z,λ,t)f2(y,λ,t)))

(16)

εfi=(xi+1-xi)-(αf1(z,λ,t)+βf2(y,λ,t)+δ(f1(z,λ,t)f2(y,λ,t)))

(17)

2 轴承摩擦故障的自记忆离散预测模型

(18)

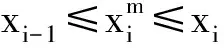
(19)

式中：αi=(βi+1-βi)/βt、θi=βi/βt为记忆参数， 其求解通过最小二乘法得到。

(20)

现给出滑动轴承摩擦故障的自记忆离散预测具体步骤(流程图见图4)如下：

(1)收集滑动轴承摩擦故障时的AE信号。采集相同间隔时间的滑动轴承AE信号，利用1.1节信号分离算法将其分离为随机声和冲击声，计算该信号的均方根值并组成监测序列，并利用式(3)～式(5)对数据预处理；

(2)反演轴承随机声和冲击声的系统微分方程。其中利用灰色系统理论GM(1,1)反演随机声的系统微分方程，冲击声系统微分方程通过冲击声均方根序列曲线函数求导获得；

(3)反演轴承AE信号的系统微分方程。根据摩擦故障曲线的变化特点，设定系统中随机声和冲击声可能的作用形式，包括线性和非线性部分，并利用双向差分原则确定方程各部分的系数；

图4 本文算法的流程图

(4)滑动轴承摩擦故障的自记忆预测方程的建立。运用自记忆原理，将反演的轴承摩擦故障系统微分方程变换成回溯为p阶的自记忆方程，利用历史数据求取方程系数，建立预测模型，并对未来轴承摩擦故障预测。

3 应用实例

为了验证本文算法预测滑动轴承摩擦故障发展趋势的有效性，分别对静载荷和动载荷中的滑动轴承实验数据建模。

3.1 静载荷滑动轴承的摩擦故障趋势预测

实验在西南交通大学静载荷滑动轴承试验台上进行，试验轴承选为S-195型柴油机主轴承，结构为剖分式，通过在轴承下部拉杆加载砝码模拟滑动轴承载荷，载荷设定为30 N·m，在轴承两端选用6010滚动轴承支承。旋转动力通过电机-无级变速箱-弹性联轴节输出。RNT-200型的声发射传感器放置于轴承盖上部平面，以500 kHz的采样频率采集滑动轴承AE信号，此外设置轴承背面温度的测量通道(将热电偶穿过轴承盖瓦孔测量轴承温度)监测滑动轴承的工作状态，实验装置如图5所示。

图5 静载荷滑动轴承实验系统示意图

实验中，启动电机至主轴转速稳定在1 500 r/min左右时，切断轴瓦的供油，模拟滑动轴承摩擦故障，同时每隔5 min采集轴承的温度和AE信号，直至轴承温度急剧升高，转速下降，表明轴承已严重损坏，此时停止实验，并规定切断润滑油路前为“-”时刻，切断油路后为“+”时刻，具体工况见表1。

在建立静载荷滑动轴承的摩擦故障自记忆预测模型时，选取断油前-7 min至断油后38 min的AE信号均方根值为建模样本，断油后43～58 min的均方根值为预测检验值。为确定回溯阶数，根据文献[14]采用试算法，确定回溯阶p=3，再分别反演随机声和冲击声系统微分方程，组成轴承摩擦故障AE信号系统微分方程为

f2(x)+1.757 6×f1(x)f2(x)

(21)

其中随机声、冲击声系统微分方程如下所示。

(22)

f2(x)=0.066 3x2-0.295 2x+4.888 3

(23)

表1 切断润滑前后滑动轴承的工况

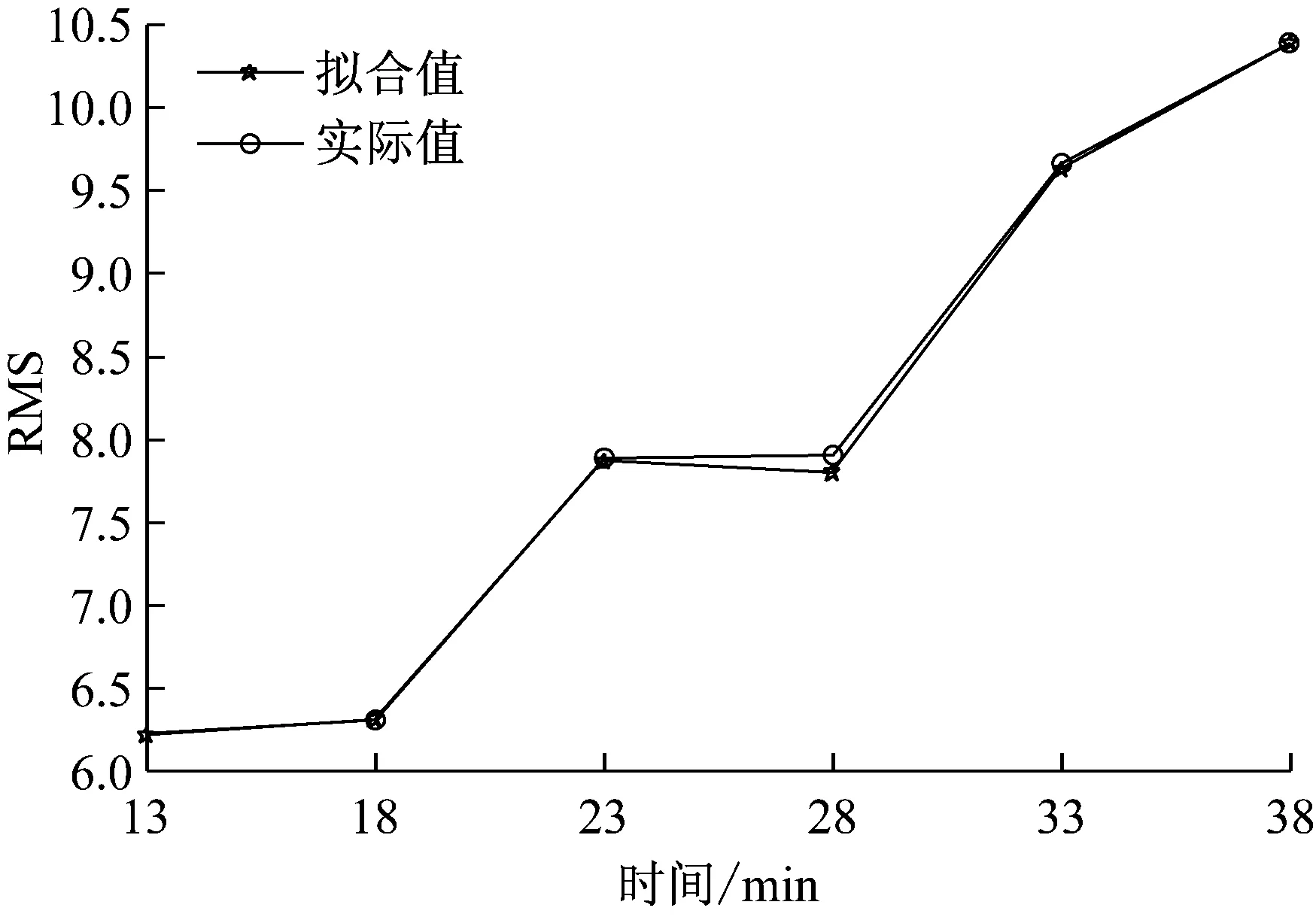
图6 AE信号均方根值与模型拟合值的比较

将微分方程式(21)作为轴承摩擦故障的动力核F(x,λ,i)，最终得到自记忆模型见式(24)所示。图6是利用此模型对断油前-7 min至断油后38 min的AE信号均方根值的拟合曲线。断油后43～58 min的摩擦故障发展预测结果见图7。可以发现，经本文算法计算的拟合样本与实际值误差范围为：0.01%～1.3%，平均误差为0.4%，预测结果中，预测误差范围0.5%～11.9%，平均误差为5.68%。为了验证本文算法的优势，再与其他预测方法比较，见表2所示。可知，原自记忆模型预测结果为：1.19%～17.92%，平均预测误差为9.93%，极限学习机预测结果为：0.92%～14.5%，平均预测误差为：8.04%，对比分析表明，本文算法预测精度高于原自记忆模型和极限学习机，由此说明，针对静载荷的滑动轴承磨损趋势预测，本文算法更有效。

(24)

式中：μ1=-1.894 9；μ2=2.849 1；μ3=-0.068 4；θ1=-7.555 9；θ2=10.475 1；θ3=1.911 1。

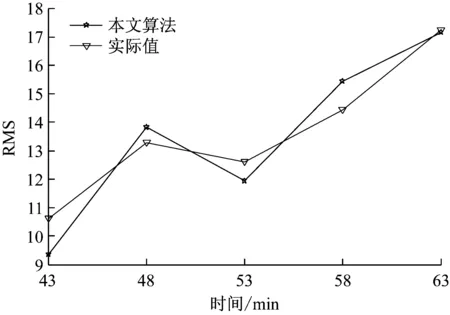
图7 AE信号均方根值与模型预测值的比较

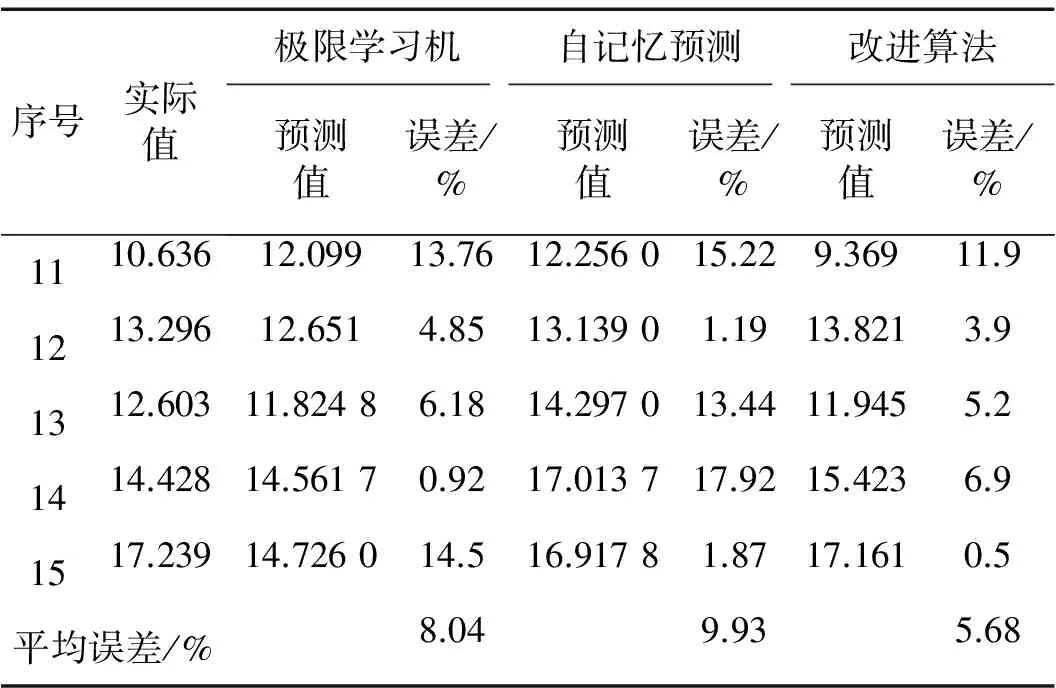
表2 预测结果比较

表3 柴油机滑动轴承实验的AE信号均方根值资料

3.2 柴油机滑动轴承的摩擦故障趋势预测

利用本文算法预测柴油机(动载荷)滑动轴承的摩擦故障发展。AE信号采集于S-195型柴油机的输出端主轴承，声发射传感器安装在靠近主轴承端的轴承座附近的机体壁上，具体实验装置见图8所示。故障转速设置为1 500 r/min，功率为P=4.62 kW，轴承摩擦故障过程借鉴静载荷实验方法，通过切断轴承润滑油路模拟轴承摩擦故障，实验中轴承不同摩擦时均方根值，如表3所示。

表4 预测结果比较

图8 柴油机滑动轴承实验系统示意图

选取断油前-2 min至断油后43 min的AE均方根序列作为自记忆预测模型样本，断油后48 min至断油后63 min的均方根值作为预测检验值。从AE信号中分离随机声和冲击声，并反演各自系统微分方程，最终得到柴油机滑动轴承摩擦故障的AE信号系统动力核：

f2(x)+0.234 7×f1(x)f2(x)

(25)

其中随机声、冲击声系统微分方程如

f1(x)=-0.056 7x+2.399 7

(26)

f2(x)=0.069 2x2-0.562 6x+5.399 8

(27)

据此建立自记忆方程，得到柴油机滑动轴承摩擦故障的自记忆预测模型见式(28)所示。通过此模型预测轴承摩擦故障的趋势变化，其中实验中断油前-2 min至断油后43 min的均方根值拟合曲线见图9所示。断油后48 min至断油后63 min的均方根值预测结果，见图10所示。可以发现，经本文计算的动载荷滑动轴承AE均方根值拟合结果与实际样本误差范围为0.1%～5%，平均相对误差为2.2%；预测结果与实际值相比，最小误差为0.9%，最大为5.3%，平均相对误差为2.5%，同时比较了原自记忆模型和极限学习机的预测结果，见表4所示。可知自记忆预测结果误差为：11.19%～21.55%，平均误差为15.58%，极限学习机预测误差范围为：2.78%～15.2%，平均误差为6.23%，对比表明，本文算法预测精度均要高于自记忆模型和极限学习机，其中本文算法预测最大误差为5.3%左右，从工程应用的角度出发，是能够满足工程应用的要求，而其他两者预测算法最大误差分别为21.55%、12.50%，基本不能满足工程要求。由此证明，本文算法适合于动载荷滑动轴承的摩擦故障的趋势预测。

综上所述，针对滑动轴承信号信息量大、信号规律分散的缺点，本文提出的滑动轴承自记忆预测模型是有效的。

(28)

式中：μ1=-0.519 8；μ2=1.406；θ1=-2.792 4；θ2=3.300 2。

图9 柴油机轴承AE信号均方根值与模型拟合值的比较

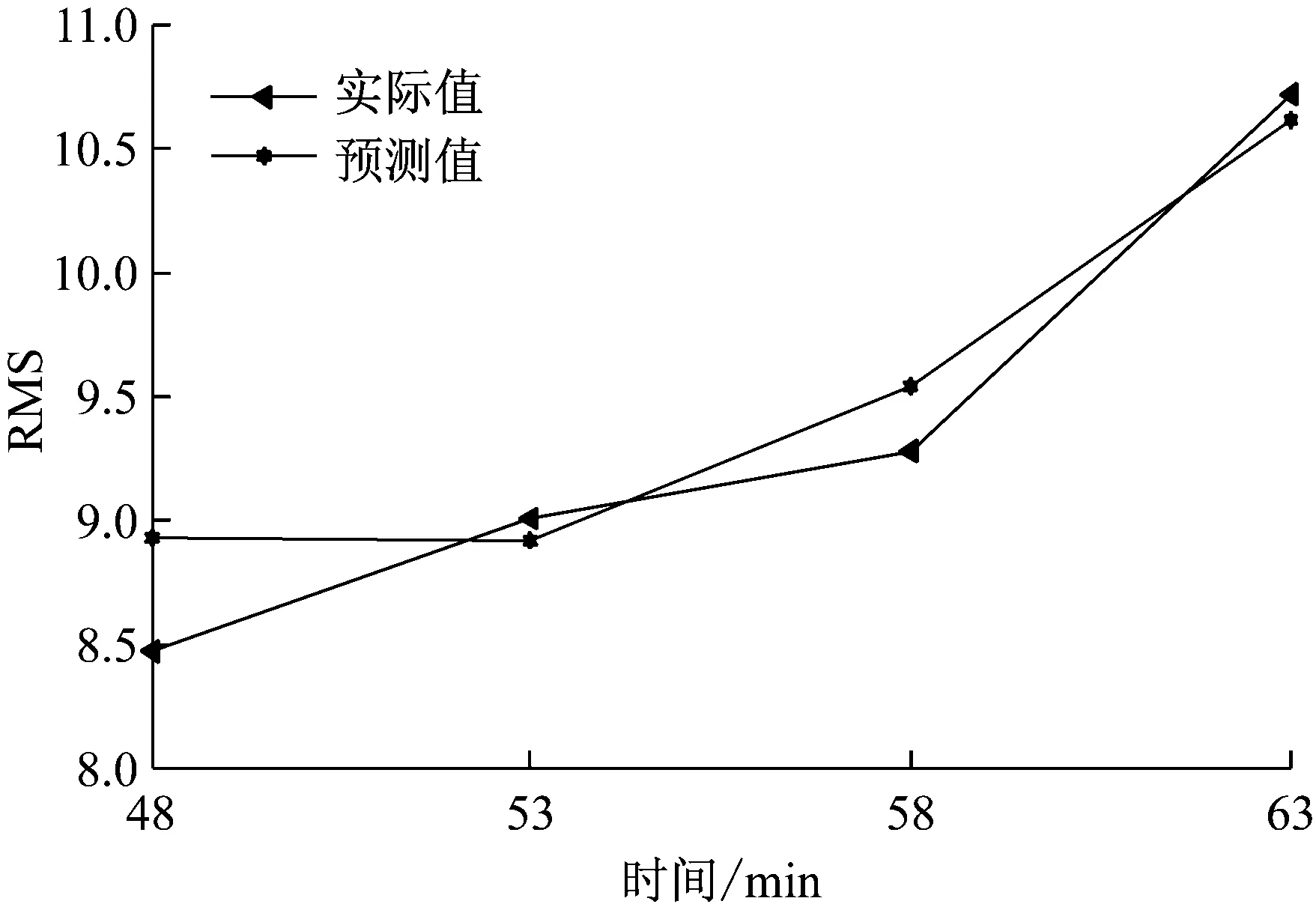
图10 柴油机轴承均方根实际值与模型预测值的比较

4 结 论

(1) 将轴承AE信号划分为冲击声和随机声，分别视为描述滑动轴承冲击性载荷和轴瓦摩擦力对轴承摩擦故障演化的特解，运用“动力系统自记忆原理”预测滑动轴承磨损趋势，取得了较好的精度，为滑动轴承摩擦故障状态预测提供了一条新的途径。

(2) 利用函数拟合、求导和灰色理论分别反演冲击声和随机声的微分方程，通过双向差分原则求取冲击声和随机声微分方程在轴承摩擦故障AE信号动力核中的系数，提出滑动轴承摩擦故障的自记忆预测模型。静载荷和动载荷的滑动轴承实例应用表明，所提方法能准确的反映滑动轴承摩擦故障的发展趋势。

[1] 陈瑞华, 杨宗伟. 基于时序AR与灰色GM模型的滚动轴承故障诊断研究[J]. 机械传动，2009, 33(6): 89-90.

CHEN Ruihua, YANG Zongwei. Roller Bearing Fault Diagnosis Based on Grey AR Combination Model[J].Journal of Mechanical Transmission, 2009, 33(6): 89-90.

[2] 肖婷, 汤宝平, 秦毅, 等. 基于流形学习和最小二乘支持向量机的滚动轴承退化趋势预测[J]. 振 动 与 冲 击, 2015, 34(9): 149-151.

XIAO Ting，TANG Baoping，QIN Yi，et al. Degradation trend prediction of rolling bearing based on manifold learning and least squares support vector machine[J]. Proceedings of the CSEE, 2015, 34(9): 149-151.

[3] 张志明,稈惠涛,徐鸿，等.神经网络组合预报投型及其在汽轮发电机组状态检修中的应用[J].中国电机工程学报,2003, 23(9): 204-205.

ZHANG Zhiming, CHEN Huitao, XU Hong, et al. Neural network based combining prediction model and its application in condition based maintenance of turbo-generator set[J]. Proceedings of the CSEE, 2003,23(9): 204-205.

[4] 李永祥,杨建国,郭前建,等.数控机床热误差的混合预测模型及应用[J].上海交通大学学报,2006,40(12): 2030-2033.

LI Yongxiang, YANG Jianguo, GUO Qianjian, et al. The application of hybrid prediction model to thermal error modeling on NC machine tools[J].Journal of Shanghai Jiaotong University, 2006,40(12): 2030-2033.

[5] WANG W，SU J Y，HOU B W，et al． Dynamic prediction of building subsidence deformation with data-based mechanistic self-memory model[J]． Chin. Sci. Bull.，2012，57(26): 3430-3435．

[6] CHEN X D，XIA J，XU Q． Differential hydrological grey model (DHGM) with self-memory function and its application to flood forecasting[J]． Sci. China Tech. Sci.， 2009，39(2): 341-350．

[7] FENG G L，CAO H X，GAO X Q，et al． Prediction of precipitation during summer monsoon with self-memorial Model[J]. Adv. Atmos. Sci., 2001, 18: 701-709.

[8] QIN P, YAN B, TAN D M. Study on fault diagnosis of sliding bearings using ae signals[J].Journal of Southwest Jiao Tong University, 2001, 36(3): 272-273.

[9] 王跃飞, 张振涛, 张波，等. 利用声发射的往复空压缩机环状阀泄露故障诊断试验[J]. 西安交通大学学报, 2012, 46(9): 26-28.

WANG Yuefei, ZHANG Zhentao, ZHANG Bo, et al. Experiment on fault diagnosis of air compressor ring valve leakage using acoustic emission[J]. Journal of Xi’an Jiao Tong University, 2012, 46(9): 26-28.

[10] 方杰. 基于采样技术的非正弦周期信号均方根值测量方法[J]. 机电技术, 2013, 5(1): 141-143.

FANG Jie. Measurement of RMS of non-sine period signal based on sampling techinques[J]. Mechanical & Electrical Techology, 2013, 5(1): 141-143.

[11] YOUNG P. Data-based mechanistic modeling，generalized sensitivity and dominant mode analysis[J]. Computer Physics Communica-tion, 1999, 117:125-129.

[12] 李新春.基于声发射监测的滑动轴承状态诊断技术研究[D]. 长沙:长沙理工大学, 2011(5): 33-34.

[13] AHARON M, ELAD M, BRUCKSTEIN A, et al. K-SVD an algorithm for designing of overcomplete dictionaries for sparse representa-tion[J]. IEEE Trans. on Signal Processing,2006,54(11): 4315-4320.

[14] 刘湘平, 谢学斌, 黄东，等. 基于动力系统自忆性原理的地下工程围岩变形预测方法[J]. 煤炭学报, 2010, 35(5): 739-744.

LIU Xiangping, XIE Xuebin, HUANG Dong, et al. Displacement prediction method of underground excavation based on self-memorization model of dynamic system[J]. Journal of China Coal Society, 2010, 35(5): 739-744.

System self-memory model for predicting friction fault trend of sliding bearings

ZHANG Junning1, ZHANG Peilin1, HUA Chunrong2, WU Dinghai1

(1. Department 7st Ordnance Engineering College, Shijiazhuang 050003, China;2. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The sliding bearings’ friction fault trend is hard to predict because bearing signals’ time series is nonlinear. To solve this problem, a friction fault trend prediction method for sliding bearings based on a system self-memory prediction model was put forward here. Firstly, according to different features of different signal excitation sources, a acquired bearing signal was separated into an impact sound and a random one. Then the function fitting, the differentiation and the grey theory were used, respectively to inverse out system differential equations of the impact sound and the random one. Bidirectional difference was used to obtain influence coefficients of different differential equations on the dynamic core of the bearing friction fault signal system. By introducing self-memory function, the dynamic core of the bearing friction fault signal system was inversed into a differential-difference equation. Further the self-memory prediction model of a sliding bearing was derived. By applying the proposed method in actual examples of sliding bearing friction fault under static and dynamic loads, the validity of the method was verified. The results provided a new way to predict the wear degradation trend of sliding bearings.

plain bearing; friction fault; development trend; nonlinear dynamic systems; signal separation; self-memory model

国家自然科学基金(51205405；51305454).

2016-03-04 修改稿收到日期：2016-04-20

张峻宁 男，硕士生，1992年生

张培林 男，教授，博士生导师，1955年生

TH117.2

A

10.13465/j.cnki.jvs.2017.11.004