一种融合多算法的面状要素空间聚类方法*

杨杰，张新长，何显锦

(1. 吉首大学生态旅游湖南省重点实验室∥城乡资源与规划学院，湖南 张家界 427000; 2.中山大学地理科学与规划学院，广东 广州 510275)

一种融合多算法的面状要素空间聚类方法*

杨杰1, 2，张新长2，何显锦2

(1. 吉首大学生态旅游湖南省重点实验室∥城乡资源与规划学院，湖南 张家界 427000; 2.中山大学地理科学与规划学院，广东 广州 510275)

空间聚类各算法均有各自的优缺点，可通过融合各算法优点达到对空间聚类算法改进优化的效果。提出了一种融合多算法的面状要素空间聚类方法。该方法利用遗传算法等优化算法优化K-means算法的初始聚类中心，利用基于密度的快速聚类算法选取K-means算法的k值，最终利用改进的K-means算法得到空间聚类结果。此外该方法针对遗传算法易受初始种群影响、运算效率低等缺陷进行了改进。经实验验证，文中方法结果稳定，算法效率、结果精准度较传统算法提升明显。

空间聚类；融合；智能优化算法；存储池

聚类分析是在没有先验知识前提下的一种重要的数据挖掘技术，其目的是找到数据的潜在自然分组[1]。而空间聚类则是聚类针对空间数据集的拓展。通过空间聚类可以发现空间数据集隐含的知识或信息，包括空间实体聚集趋势、分布规律和发展变化趋势等[2-3]。目前，国内外学者对于空间聚类方法进行了较为深入的研究，其现已在地理空间数据挖掘及知识发现等领域中广泛应用[4-7]。

顾及专题属性特征的空间聚类才能完整的获得空间数据集隐含的知识和信息，但其算法也更复杂。有学者提出了基于多约束的空间聚类方法[8]，并有学者提出了双重约束下的自组织空间聚类方法[9]，但研究更多的是针对点群的空间聚类，或者考虑的是空间要素空间绝对位置。本文主要研究面状实体的地理空间聚类问题，且其中单个面状实体几何形态、位置对全局问题不太重要，但需考虑面状实体邻接，并且重点考虑专题属性特征在空间分布上的差异的真实地理空间问题。空间自相关是针对上述问题的一种解决方式，其是对空间单元属性值聚集程度的度量与评价，可以揭示空间要素的区域结构形态[10]。该理论经多年发展逐渐成为地理空间分析重要方法，不少学者也在不断拓展其应用领域[11-12]。

常用聚类方法常难以解决现实地理空间的复杂优化问题，其可通过包括遗传算法(GA)在内的智能优化算法解决[13-14]。其也可和聚类算法融合，将聚类算法的目标函数作为其适应度函数的重要部分来指导进化，获得最佳聚类方案[15]。

本文首先利用GA等算法优化K-means算法的相关缺陷，并充分考虑空间数据的专题属性特征，优化适应度函数，进而得到最优的空间聚类结果，且对GA的相关缺陷进行了改进，提出了一种融合多种算法的，针对面状要素空间聚类问题的方法。

1 基本算法

针对空间要素的空间聚类算法各自的优缺点进行融合优化，这首先需要深入了解各算法的工作机制，找出其融合优化的突破口。

1.1 K-means

K-means是一种经典的快速聚类算法，应用极其广泛，但其有k值需事先给定、初始聚类中心对最终聚类结果影响较大且易陷入局部极值等缺陷。其基本思想为通过迭代将n个对象聚类为k个簇(类)(k≤n)，最终使簇(类)内相似度较高，簇(类)间相似度较低。该算法将n个样本对象xi(i=1,2,…,n)分为k个类，并求每类的聚类中心Ks(s= 1,2,…,k)，最终使得目标函数最小。常用的目标函数为：

(1)

式中，dis(xi,Ks)是xi与Ks之间的欧氏距离。

1.2 GA

GA通过模拟自然界生物进化机制得到某问题的最优解。GA首先将问题的可能解集进行相关编码操作并形成初始种群，并根据具体问题构造相应的适应度函数f(x)。对每代种群根据f(x)计算种群个体适应度函数值，再进行包括选择、交叉和变异的遗传操作产生下一代种群，之后迭代进化直到符合条件终止，最终代种群即最优解，再进行解码操作。

GA虽有收敛的全局性、无需对适应度函数限制条件等优点使其应用广泛，但因其较容易陷入“早熟”、计算后期效率较低且容易产生无效解等缺陷，还需相关优化与改进。

1.3 爬山法

爬山法是一种能快速收敛于局部最优解且效果较好的搜索算法。其和GA都属于优化算法，对单峰问题相当有效。其具有初始搜索点对结果影响较大、只能搜索到局部最优等缺点，但其可和其他优化算法融合，发挥局部寻优作用。算法首先需根据具体问题构造适应度函数f(x)，其主要流程[16]为：

1)在解集空间中随机选取一个点x0，令xnow(0)=x0，即将其作为当前点，并设置迭代代数计数器t=0；

2)在xnow(t)邻域内随机生成一个点xnei(t)，即xnow(t)的邻居点；

3)根据适应度函数，得到f(xnow(t))与f(xnei(t))，并令xnow(t) = arg max(f(x(t)))；

4)重复2)、3)，直到f(xnow(t))=f(xnow(t-1))，则终止迭代，并将xnow(t)作为最优解。

1.4 基于密度的快速聚类算法

基于密度的聚类方法因其成功克服了基于距离聚类只能识别“球形簇”的缺点，可发现任意形状数据集的聚类，且对“噪声”不敏感等特点而应用范围广泛。文献[17]提出了一种新的基于密度的聚类算法，其认为簇(类)中心被比其密度低的点包围，且这些点离该簇(类)中心的距离比其他簇(类)中心近。具体的算法流程如下：对于样本中每一个数据点i需计算两个量，点i的局部密度ρi和点i与比其密度更高点之间的最小距离δi。与i点距离在dc的范围内的点越多，ρi越大，dc为截断距离。ρi可用cut-off kernel(离散值)定义，也可用Gaussian Kernel(连续值)定义，因后者使不同数据点具有的相同局部密度值概率更小，所以本文使用后者定义局部密度。ρi和δi可表示为：

(2)

(3)

对于密度最大的点，可得到

(4)

式中，dij为点i与点j的距离。文献[17]认为dc为所有数据点之间距离值按从小到大排列后的前1%～2%区间，本文取其为1.5%。对于每一个数据点i来说，均可得到(ρi,δi)，其中ρi和δi均进行了归一化处理。ρi和δi均较大的点则为聚类中心。可定义γi=ρiδi，即综合考虑ρi和δi，γ越大，则越可能是聚类中心。绘制出以点顺序号为横轴，γ值为纵轴的决策平面图后，会发现从非聚类中心到聚类中心有明显的跳跃，此时可较易判断出聚类中心点，且这种决策图可用于其他聚类算法的数据预处理。剩余点的类标与到比自身局部密度大且距离最近的点一致。此聚类算法原理简单、处理效率高，且易与其他算法结合。

2 融合多算法的空间聚类

2.1 K-means与相关算法的融合

从上可以看出K-means具有受初始聚类中心影响较大，且需人工选择k的大小等缺陷。可结合遗传算法的全局寻优性得到最优的初始聚类中心，并可利用1.4提及的快速聚类算法结合聚类结果的可解释性选取k值。

2.2 GA与爬山法的融合及其改进

首先，GA的初始种群对整个GA运行的性能和结果都有着巨大的影响，本文利用爬山法得到的局部最优解作为GA的初始种群，进而使GA整体效能得到优化。第二，在解决实际问题时，适应度函数通常较为复杂，且为了保证种群多样性，种群规模一般较大，这导致GA计算效率尤其在进化中后期急剧下降，本文提出建立解集与其对应适应度值的映射关系存储池概念，规避GA重复无效解的计算，大大提高了GA的运算效率。第三，GA编码方式因研究对象为自然数而采用自然数编码，其较传统二进制编码方式更直观、计算量较小且不需特别编码与解码，算法效率高。第四，本文采用精英选拔法，较之传统轮盘赌选择算子其能保证每代都将最优的子代信息保留下来。

2.3 顾及面状要素属性特征的空间聚类

对于面状要素属性值聚集程度的度量可以用空间自相关系数表征，其有全局和局部两种指标，其中全局指标可用于描述某现象的整体分布情况。全局自相关指数中最常用的是Moran’I指数[10]，可表达为：

(5)

式中，n为参与分析的面状要素数目，面状要素在i和j处的属性值为xi和xj，Wij为空间权重矩阵，当面状要素i和j邻接时，Wij为1，否则为0。上式取值范围为-1～1，值越接近1表示越集聚，越接近-1表示越离散，值趋近0时表示随机分布。顾及专题属性特征的面状要素空间聚类能更真实地表达现实问题，因此本文构造的适应度函数充分考虑了面状要素的空间自相关，以期更好的模拟真实情况。

2.4 算法基本流程描述

本文算法详细流程如下：

1)输入n个面状对象pi(i=1,2,…,n)，pi的专题属性值对象为xi，xi为一个一维数组，内有元素m个。基于式(2)-(4)得到每个xi的(ρi,δi)，并令γi=ρiδi，得到γ值决策图，根据图中跳跃点数，得到输入数据集可分为k类；

2)构建进化算法的适应度函数：

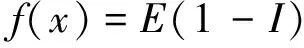
(6)

其中E为输入数据集xi的K-means聚类的目标函数值(见式(1))，Im为其对应的空间数据集的Moran’I指数(见式(5))，且I=∑Im/m；

3)根据1.3中的爬山法得到面状对象pi的局部最优解，即局部最优聚类中心k个对象；

4)重复3)过程M次，得到局部最优解集P(1)，将其作为GA的初始种群，个数为M，每个种群个体含有k个对象，并设置最大进化代数T、进化代数计数器t=1；

5)根据f(x)计算种群个体P(t)的适应度函数；

6)根据相应的选择算子、交叉算子、变异算子对种群进行选择、交叉、变异操作，得到下一代种群P(t+1)。其中选择算子为精英选拔，即将种群个体按f(P(t))值大小排序，根据优选率选择部分最优个体作为下代种群P(t+1)的成员。小于变异率进行变异操作，否则进行交叉操作，将P(t)经过变异、交叉操作后得到的种群个体补充进P(t+1)。交叉算子的交叉点为随机交叉点，变异算子为按步长变异；

7)若t≤T则重复5)、6)过程，直到t>T，则在P(T)中将获得最优适应度fmax个体作为全局最优解并解码输出，并终止重复；

8)将全局最优解的k个对象作为聚类中心，进行K-means聚类，得到pi的聚类结果。

3 实验分析

3.1 爬山法优化GA初始种群实验

首先对爬山法优化GA初始种群的效能进行相关实验。实际问题为从1到300中随机选可重复的24个数字，并选取3次，依次得到3个一维数组，即每个数组包含随机的24个数字，求这3个数组最小值的和及其对应的数字(下称为因子)。此实验保证了每次实验的独立性，并能快速获得真实解以进行比对。本文分别使用爬山法、GA、爬山GA优化法(下称优化法)进行实验，将结果与真实解比对获得其正确率(见表1)，表1中单因子代表只要有一个数组中因子正确则计为结果正确，全因子代表要3个数组因子全正确才计为结果正确。实验轮数代表第几轮实验。本实验共计8轮，每轮均运行算法1 000次来统计结果，这样结果比较可信。

表1 各算法正确率统计表

将表1中每种算法结果取平均值，可得爬山法、GA、优化法单因子/全因子正确率(%)分别为14.3/0.1，63.4/25.9，90.2/72.5，可以得出优化法较传统GA、爬山法大大提高了获得正确解的能力。

3.2 整体算法实验

武陵山片区作为国家扶贫战略重要的经济协作区，对其按县域经济进行分类进而指导区域经济协调发展具有重要意义。本文选取武陵山片区71个县(区)作为研究对象，因研究对象总体状况在短时间内沿时间序列空间差异变化不大，因此选取其近期某一年例如片区发展启动年的一、二、三产经济数据为代表作为研究数据。

本文首先将71个县(区)2013年一、二、三产数据输入，得到其三维空间中的分布散点图(见图1)，再根据式(2)-(4)，得到(ρi,δi)，i=1,2,…,71，其中ρi与δi均进行了归一化处理，再定义γi=ρi*δi，得到γ值决策图(见图2)。从图2可以看出，其点分布有一个明显的跳跃，在跳跃虚线之上有3个点，再结合聚类结果的可解释性，将研究数据聚类数定为3类。

然后根据2.4的算法流程最终获得最优聚类中心与聚类结果。但在实验中由于现实问题复杂，多次计算Moran’I指数等原因导致算法效率极低，急需优化。本文利用存储池概念优化算法，即将所有上代种群个体与其对应的适应度值的映射关系存入存储池，再将本代种群与存储池中的种群进行比较，如有相同值，则直接读取其对应的适应度值，如没有则计算其适应度值并存入存储池，这使得算法效率大大提高。本文以GA参数设置为初始种群为20、步长为1、变异率0.01、优选率0.2、进化代数30为例进行了相关实验，实验环境为Win7系统，CPU为3.1 GHz，内存8 GB，实验结果如表2，表中记录前15代的奇数代时间耗费：

GA优化前第15代所用时间已超过1 h，累计时间将近10 h，这对于数据量并不太大的研究对象来说已无法接受，而优化后每代耗费时间大大下降，且较平稳。

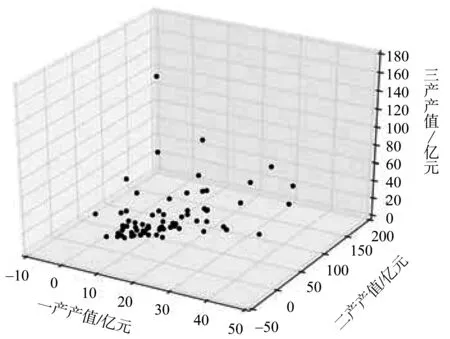
图1 数据集散点图Fig.1 Scatter plot of data set

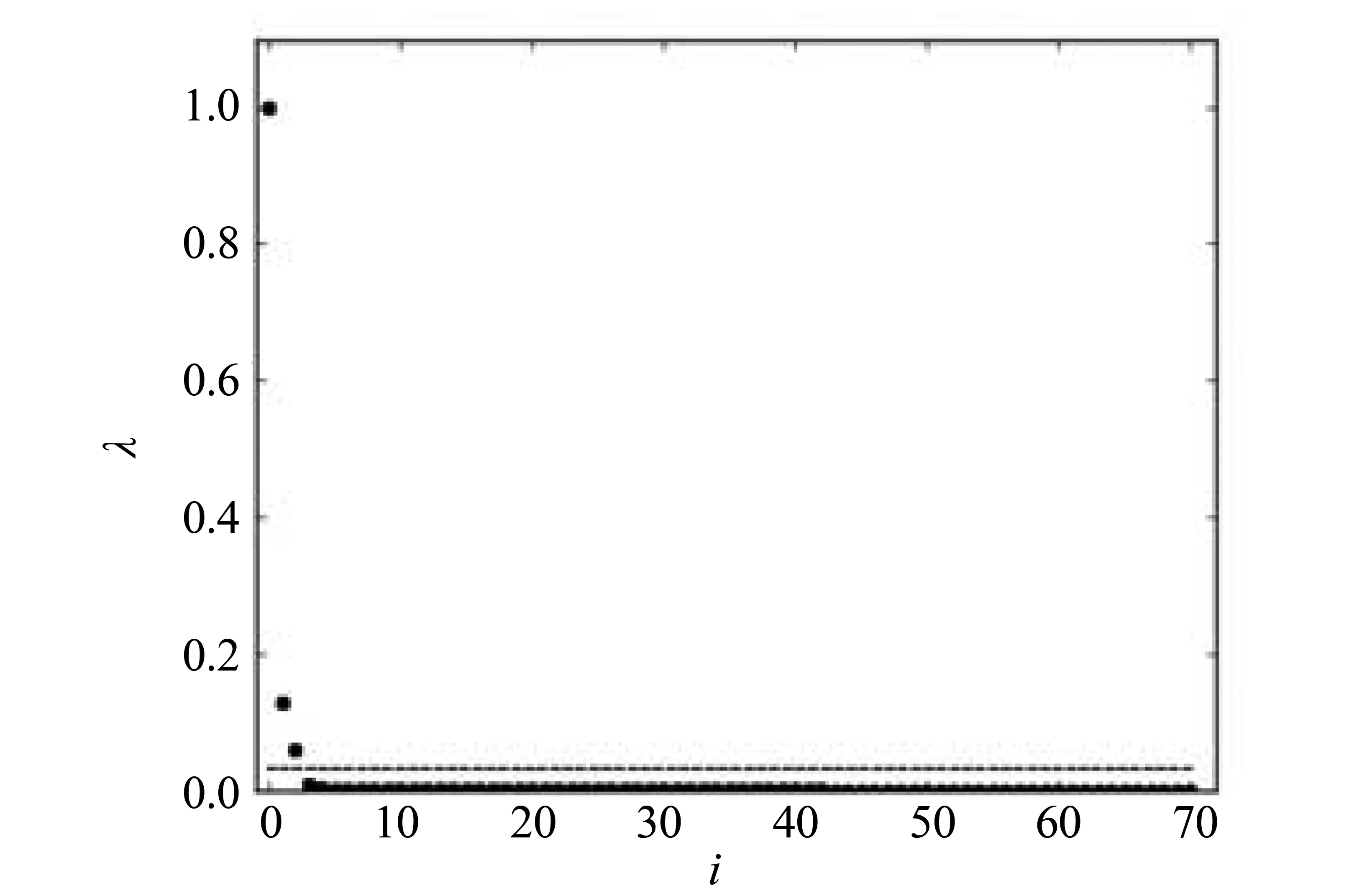
图2 γ值决策图Fig.2 Decision graph of gamma value

因GA的变异算子对GA影响较大，本文的最终优化GA采用3种参数实验，初始种群均为50、进化代数均为80、优选率均为0.2，第一种步长为1，变异率为0.01，第二种步长为1，变异率为0.2，第三种步长为2，变异率为0.2，实验结果如图3。

从图3可得第一种参数下优化GA最快得到了全局最优解，且3种参数的全局最优解的最佳个体适应度都相等，实际上3种参数下全局最优解相同。

最终的聚类分配结果，其区域空间分布如图4，另对研究数据使用常用的K-means方法进行对比，K-means方法聚类结果十分不稳定，本文取其一次较佳结果得到区域空间分布如图5，而本文提出的算法聚类结果十分稳定。

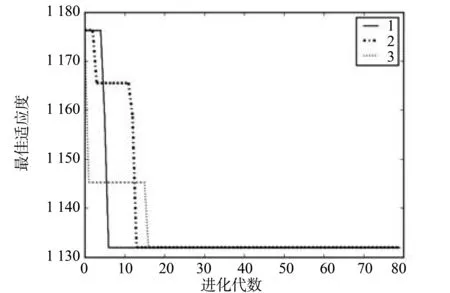
图3 三种参数GA的最佳适应度变化曲线Fig.3 Change curve of the genetic algorithm’ optimal fitness with three kinds of parameters

虽然有针对特定空间聚类算法结果检验的相关研究[18]，但目前尚未有通用的有效评价指标对空间聚类结果进行定量评价[8, 19]，本文主要通过领域内先验知识进行对比来判别结果。从上图可看出，本文提出的方法结果较K-means方法更符合实际，且结果稳定。K-means聚类结果面状要素1类太少，不利于带动整个区域的发展，2类比较少，且分布零散，因不相邻地区较难进行经济融合，其不利于区域经济协作，进而丢失大规模抱团发展机遇。

表2 GA优化前后时间耗费统计表

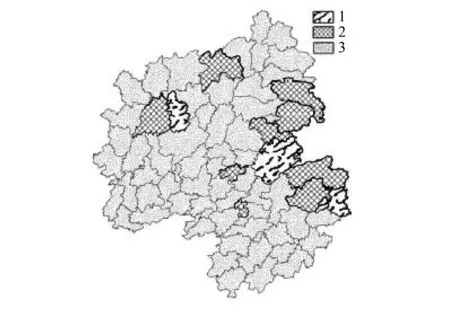
图5 K-means聚类结果Fig.5 Clustering result of K-means

本文聚类结果1类所在区域均位于各县域一、二、三产均值排名前列，3类所在区域均位于各县域一、二、三产均值排名末段，聚类结果的1、2、3类排序基本与各县域经济实力排序吻合，因此本文聚类结果与各县域一、二、三产数据空间分布集聚特征较为相似，说明聚类结果与实验数据吻合度较高。

4 结 论

本文提出的多算法融合的面状要素空间聚类方法综合了多种算法的优点，通过算法融合，弥补相应算法缺点，提高了相关算法的效率。整体方法更符合某些地理空间现实情况，原理简单，较易实现，具有较好的鲁棒性，自动化程度较高，算法效率、结果精度提升明显。该方法有如下几个特点：

1)对于K-means的k选择与聚类中心选择通过相关算法得到，剔除了人工与随机因素，更为科学。

2)GA的初始种群使用爬山法优化，且利用存储池概念优化了GA效率，这使得GA在解决复杂现实问题时得到的解更精确，效率更高。

3)方法得到的最终解稳定，不因参数等外界因素的改变而改变。

[1] JAIN A K. Data clustering:50 years beyond K-means[J]. Pattern Recognition Letters，2010，31(8): 651-666.

[2] MILLER H，HAN J. Geographic data mining and knowledge discovery[M].2nd ed. London：CRC Press，2009.

[3] LI D R，WANG S L，LI D Y. Spatial data mining：theory and application[M]. Berlin：Springer，2015.

[4] KIM H S，KIM J H，HO C H，et al. Pattern classification of typhoon tracks using the fuzzy C-means clustering method[J]. Journal of Climate，2011，24(2)：488-508.

[5] CRACKNELL M J，READING A M. Geological mapping using remote sensing data：A comparison of five machine learning algorithms，their response to variations in the spatial distribution of training data and the use of explicit spatial information[J]. Computers & Geosciences，2014，63(1)：22-33.

[6] HUI C M E，LIANG C. The spatial clustering investment behavior in housing markets[J]. Land Use Policy，2015，42(1)：7-16.

[7] 黄敏，李尔达，袁媛，等. 基于路网拓扑的聚类分析算法研究与实现[J] . 中山大学学报(自然科学版)，2015(6)：99-103. HUANG M，LI R D，YUAN Y，et al. Research and implementation of clustering analysis algorithm based on road network topology[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni，2015(6)：99-103.

[8] 刘启亮，邓敏，石岩，等. 一种基于多约束的空间聚类方法[J]. 测绘学报，2011，40(4)：509-516. LIU Q L，DENG M，SHI Y，et al. A novel spatial clustering method based on multi-constraints[J]. Acta Geodaetica et Cartographica Sinica，2011，40(4)：509-516.

[9] 焦利民，洪晓峰，刘耀林. 空间和属性双重约束下的自组织空间聚类研究[J]. 武汉大学学报(信息科学版)，2011，36(7)：862-866. JIAO L M，HONG X F，LIU Y L. Self-organizing spatial clustering under spatial and attribute constraints[J]. Geomatics and Information Science of Wuhan University，2011，36(7)：862-866.

[10] GETIS A. Reflections on spatial autocorrelation[J]. Regional Science and Urban Economics， 2007，37(4)：491-496.

[11] MARROT P，GARANT D，CHARMANTIER A. Spatial autocorrelation in fitness affects the estimation of natural selection in the wild[J]. Methods in Ecology and Evolution，2015，6(12)：1474-1483.

[12] GRIFFITH D A，CHUN Y W. Spatial autocorrelation in spatial interactions models: geographic scale and resolution implications for network resilience and vulnerability[J]. Networks and Spatial Economics，2015，15(2)：337-365.

[13] CUI M S，PRASAD S，LI W，et al. Locality preserving genetic algorithms for spatial-spectral hyperspectral image classification[J]. Selected Topics in Applied Earth Observations and Remote Sensing，IEEE Journal of，2013，6(3)：1688-1697.

[14] 赵元，张新长，康停军. 多叉树蚁群算法及在区位选址中的应用研究[J]. 地理学报，2011，66(2)：279-286. ZHAO Y，ZHANG X C，KANG T J. An ant colony algorithm based on multi-way tree for optimal site location[J]. Acta Geographica Sinica，2011，66(2)：279-286.

[15] AGUSTI L E，SALCEDO-SANZ S，JIMENEZ-FERNANDEZ S，et al. A new grouping genetic algorithm for clustering problems[J]. Expert Systems with Applications，2012，39(10)：9695-9703.

[16] RUSSELL S J，NORVIG P. Artificial intelligence:a modern approach[M]. 2nd ed. New Jersey: Prentice Hall，2003.

[17] RODRIGUEZ A，LAIO A. Clustering by fast search and find of density peaks[J]. Science，2014，344(6191)：1492-1496.

[18] 唐建波，刘启亮，邓敏，等．空间层次聚类显著性判别的重排检验方法[J]. 测绘学报， 2016，45(2)：233-240. TANG J B，LIU Q L，DENG M，et al. A permutation test for identifying significant clusters in spatial dataset[J]. Acta Geodaetica et Cartographica Sinica，2016，45(2)：233-240.

[19] YUE S H，WANG J S，WU T，et al. A new separation measure for improving the effectiveness of validity indices[J]. Information Sciences，2010，180(5)：748-764.

A spatial clustering method fusing multiple algorithms for area feature

YANGJie1, 2,ZHANGXinchang2,HEXianjing2

(1. Key Laboratory for Ecotourism of Hunan Provice∥College of Urban-Rural Resources and Planning Sciences，Jishou University，Zhangjiajie 427000，China； 2.School of Geography and Planning，Sun Yat-sen University，Guangzhou 510275，China)

Each spatial clustering algorithm has its own advantages and disadvantages. Spatial clustering algorithms can be improved and optimized through the fusion of the algorithms’ advantages. A spatial clustering method fusing multiple algorithms for area feature is proposed in this paper. This method optimizes the initial cluster centers of K-means algorithm by using genetic algorithm and other optimization algorithms, selects thekvalue of K-means algorithm by using a fast clustering algorithm density-based, and then obtains spatial clustering results with improved K-means algorithm. It improves the genetic algorithm which is easy to be affected by the initial population and has low efficiency. The experimental results indicate that the method is steady, and is more efficient and accurate compared to the traditional algorithm.

spatial clustering；fusion；intelligent optimization algorithm；storage pool

10.13471/j.cnki.acta.snus.2017.03.019

2016-05-12 基金项目：国家自然科学基金重点项目(41431178)；湖南省社科基金(14YBX026)；生态旅游湖南省重点实验室开放基金(JDSTLY201207)

杨杰(1985年生)，男；研究方向：空间数据挖掘，建模与分析；E-mail:yangj257@mail2.sysu.edu.cn

张新长(1957年生)，男；研究方向：空间数据智能化管理与数据库自动更新;E-mail:eeszxc@mail.sysu.edu.cn

P208

A

0529-6579(2017)03-0134-06