无标度网络累积分布的新方法*

王晓敏，姚兵，2

(1. 西北师范大学数学与统计学院，甘肃 兰州 730070; 2. 兰州交通大学电子与信息工程学院，甘肃 兰州 730070)

无标度网络累积分布的新方法*

王晓敏1，姚兵1，2

(1. 西北师范大学数学与统计学院，甘肃 兰州 730070; 2. 兰州交通大学电子与信息工程学院，甘肃 兰州 730070)

以算法的方式给出了具有无标度性的极大平面图网络，计算了极大平面图网络模型的顶点累积分布和边累积分布，并验证二者的等价性。此外，按照混合方式的不同，提出了新的统计指标:边点混合累积分布。随后，提出猜想：采用线性混合方式的边点混合累积分布与顶点累积分布是等价的。此猜想为全方位、多角度的探讨无标度网络提供了新视角。

无标度网络；顶点累积分布；边累积分布；幂律分布

自然界、生物界、工程界以及人类社会中的大量复杂系统成为当今的复杂网络科学的热门研究对象，如 Internet[1]、社交网络等[2]。复杂网络的规模随时间的推移不断变化，给全方位的探讨复杂网络的结构及功能带来了很大的障碍。因此，为复杂网络建立合理的演化模型，对于深入考查其拓扑结构、网络优化、网络资源的合理分配以及网络信息安全等具有重要的指导意义。一般情况下，复杂网络的规模较大，在缺少关于其节点间连接关系的前提下，最简单、最直接的复杂网络演化模型应该是 Erdös 和 Rényi的随机图模型。在该模型中，每个节点获得连接的机会均等，节点的度(即该节点连接的边数)服从 Poisson 分布。网络技术、计算机技术以及数据处理技术的提高使得人们有可能获得许多实际网络中节点间的连接关系，如万维网、神经网络以及物流网络等。对这些实际网络进行实证研究，发现这些复杂网络存在一个共同的特点，网络的节点的度数存在极大的差异，节点的度分布服从幂律分布，而不是像随机图模型所预测的那样服从 Poisson 分布，这样的复杂网络称为无标度网络。

自1999年 Barabási和Albert发表有关复杂网络的无标度性的文章以来，在此后的十几年里，各行各业的学者成功的运用复杂网络理论解决了一些问题，使得复杂网络已经渗透到许多不同领域的学科[3-6]。从微观的细胞网络到宏观的宇宙网络，发现许多具有无标度性质的网络。在验证幂律分布的时候，不少说明网络是无标度网络的文章均采用文献 [7] 中的技术手段，计算网络模型的顶点累积分布，验证顶点累积分布服从幂律分布，依据此标准来确定具有无标度性，文献[8] 给出了一类递归集团树的无标度性，文献[9]构造了全边增长网络并给出了寻找其最多叶子生成树的算法。文献[10]探讨一类增长网络模型的生成树，文献[11]中讨论了无标度网络的平衡集。文献[12]将低维的阿波罗网络推广到高维阿波罗网络，并验证了高维阿波罗网络的无标度性。文献[13] 的作者验证了极大平面图的 Sierpinski 网络的无标度性。此外，文献[14]的作者提出一个验证幂律分布的新方法，即边累积分布服从幂律分布，进而说明网络是无标度网络。此外，一些学者讨论了对网络添加简单图所构成的网络的性质，两个网络之间的运算，以及寻找网络的最大叶子生成树的算法等[15-17]。

用文献 [13] 建立的极大平面图网络模型，本文计算该网络模型的顶点累积分布和边累积分布，并证明边累积分布和顶点累积分布是等价的。随后，提出了按照混合方式区分的新的统计指标，即边点混合累积分布，并对边点混合累积分布的幂律特性进行计算和证明。

1 主要结论

1.1 Sierpinski 网络的建立

本小节先引入经典的Sierpinski 分形垫(也称Sierpinski三角形)。Sierpinski分形垫可以使用迭代的方法进行构造。用t表示迭代的次数，令S(t)表示经过t步演化后得到的Sierpinski分形垫，则其具体的构造过程可以用下面的Sierpinski算法给出。

Sierpinski-算法

初始化。t=0，S(0)是一个等边三角形。

运算。t=1，连接等边三角形S(0)的各边的三等分点，从而将原等边三角形分成 9 个小等边三角形，然后“舍弃”中间的3个倒立的小三角形，便得到S(1)。未舍弃的三角形称为活动三角形。

迭代。继续对剩下的6个活动小三角形按上面同样的方法继续分割，并“舍弃”中间倒立的3个小三角形，如此不断地重复“分割”与“舍弃”的过程，便得到Sierpinski三角形S(t)。

Sierpinski 分型垫的具体生长过程在图1 中给出。

图1 Sierpinski分型垫的构造过程S(0), S(1), S(2) (左边t=0, 中间t=1, 右边t=2)Fig.1 The construction process of the Sierpinski gasket S(0), S(1), S(2)(left t=0, middle t=1, right t=2)

根据 Sierpinski 分形垫，通过如下映射方法可构造 Sierpinski 网络:将 Sierpinski 分形垫中每个被删除的三角形映射为网络节点，将 Sierpinski 分形垫的所有被删除的三角形与初始等边三角形相交映射为网络的边。为了保持一致，分形垫中初始等边三角形的三条边也分别对应 3 个不同的节点。基于S(0)、S(1)、S(2)的生长过程可以构造出相应的Sierpinski网络在图-2 给出解释和说明。这样，便得到了一个Sierpinski网络。由于该网络描述了Sierpinski分形垫中被删除三角形边的接触关系，所以称之为Sierpinski网络。Sierpinski网络的N(0)、N(1)、N(2)如图2所示。

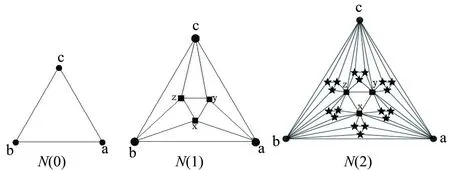
图2 Sierpinski 网络N(0), N(1), N(2)(圆点为t=0, 正方形点为t=1, 五角星点为t=3)Fig.2 The Sierpinski network N(0), N(1), N(2)(the circle vertices denote t=0, the square vertices represent t=1, the pentagram vertices stand for t=2)

1.2Sierpinski网络的参数

根据Sierpinski网络模型的构造来计算该网络的阶数和边数，令Δv(t),Δe(t)和Δ(t) 分别表示在t时刻网络新增加的节点数目以及新增的边数目和新增的活动三角形的数目。把按照S(t) 的构造演化出来的Sierpinski网络记为N(t)，根据N(t)的构造，t-1时刻的每一个活动三角形在t时刻将产生 6个活动三角形。因此，可推算出Δ(t)=6Δ(t-1)，又因Δ(0)=1，所以Δ(t)=6t。此外，在t-1时刻每一个活动三角形将产生3个新的节点和9条新边，容易计算，

(1)

对于任意的t>0，用V(t)，E(t) 分别表示Sierpinski网络N(t)的节点集合和边集合，则可用nv(t),ne(t)分别表示网络模型N(t) 在t时刻总的节点数目和总的边数目。因此，有

(2)

当t足够大的时候，Sierpinski 网络N(t)的平均度=2ne(t)/nv(t)→6，说明该网络是一个稀疏网络，也就是说，网络中实际存在的边数远远小于可能存在的最大边数nv(t)×[nv(t)-1]/2，并且与现实生活的网络现象相吻合。

1.3Sierpinski网络的度分布

节点i是在ti时刻进入网络N(t) 的，此时，节点i的度为4。令Δ(i,t) 表示t时刻产生的活动三角形的个数，这些三角形在t+1时刻将产生的新节点与节点i相连。在ti时刻，Δ(i,ti)=3，根据网络的迭代过程，可以看出网络N(ti) 新增加的一个活动三角形将会在下一时刻形成 6个新的活动三角形。令ki(t) 表示t时刻节点i的度数，因ki(t) 与Δ(i,t) 的关系满足Δ(i,t)=ki(t)-1，又有Δ(i,t) =3Δ(i,t-1)和Δ(i,ti) =3，则在t时刻，节点i的度为ki(t)=3t-ti-1+1，从而得到Sierpinski网络N(t)的度谱(见表1)。

表1 N(t) 的度谱

表1 告诉Sierpinski网络N(t) 的度分布是离散的文给出一种新的累积分布

将ti=t+1-ln(k-1)/ln 3代入上式，得

将ti=t+1-ln(k-1)/ln 3 代入上式，得

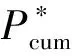
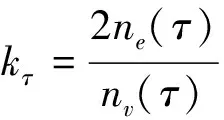
同理，可证明

分析可知，在τ足够大时，τ→，得β≅1。因此，顶点累积分布和边累积分布是等价的。除了顶点累积分布之外，还可以用边累积分布来确定网络N(t) 是无标度网络。

1.4 边点混合累积分布

本小节给出新的统计指标，叫做边点混合累积分布，有以下 3 种形式:

(i) 边点数乘累积分布

用ti=t+1-ln(k-1)/ln 3替换上式中的ti，整理可得

(ii) 边点差累积分布

用ti=t+1-ln(k-1)/ln 3替换上式中的ti，整理可得

(iii) 边点根式累积分布

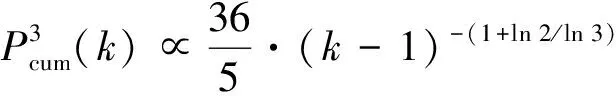
2 讨 论

本文借助于现有的无标度网络模型，验证了顶点累积分布和边累积分布的等价性。基于不同的混合方式，提出3种新的累积分布。为探索网络的无标度性提供了一个新的方法。大多数验证无标度网络的方式是说明顶点累积分布服从幂律分布。本文发现虽然采用不同的方式计算累积分布，例如顶点累积分布和边累积分布，仍可以得出网络服从无标度网络的结论。因此，我们猜想：顶点累积分布服从幂律分布和边累积分布服从幂律分布都可以作为来确定网络是无标度的依据，换句话说，顶点累积分布和边累积分布是等价的。但边点混合累积分布因混合的方式不同所得到的累积分布也不尽相同，需进行深入研究和实证。

[2] 吴泓润，覃俊，易云飞，等. 基于优化理论的社区无标度网络模型[J]. 计算机学报, 2015, 38(2)：337-348. WU H R, QIN J, YI Y F, et al. A model of community-structure and scale-free network based on optimization theory [J]. Chinese Journal of Computers, 2015, 38(2): 337-348.

[3] BANCONI G, BARABSI A L．Competition and multiscaling in evolving networks [J]．Europhysics Letters, 2001,54(4): 436-442．

[5] JUNG S, KIM S, KAHNG B. Geometric fractal growth model for scale-free networks [J]. Physica Review E 2002, 65(2): 056101.

[6] VIJAYAN A, BEULA J S. Edge-vertex dominating sets and edge-vertex domination polynomials of cycles [J]. Open Journal of Discrete Mathematics, 2015, 5(4): 74-87.

[7] NEWMAN M. The structure and function of complex networks [J]. SIAM Review, 2006, 45(2): 167-256.

[8] COMELLAS F, FERTIN G, RASPAUD A. Recursive graphs with small-world scale-free properties [J]. Physical Review E, 2004, 69(3 Pt 2): 281-285.

[9] 王晓敏, 赵喜杨, 姚兵. 全边增长网络模型的生成树[J]. 中山大学学报(自然科学版), 2016, 55(1): 48-53. WANG X M, ZHAO X Y, YAO B. Spanning trees of totally edge-growing network models [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(1): 48-53.

[10] 张婉佳, 刘霞, 姚兵. 一类增长网络模型的生成树[J]. 厦门大学学报(自然科学版), 2015, 54(4): 497-501. ZHANG W J, LIU X, YAO B. Spanning trees of a class of growing network models [J]. Journal of Xiamen University (Natural Science), 2015, 54(4): 497-501.

[11] 刘霞, 姚东任, 姚兵，等. 探讨无标度网络的平衡集[J]. 中山大学学报(自然科学版), 2015, 54 (1): 19-23. LIU X, YAO D R, YAO B, et al. On balanced sets in scale-free networks (graphs) [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2015, 54 (1): 19-23.

[12] ZHANG Z Z, COMELLAS F, FERTIN G, et al. High dimensional apollonian networks [J]. Journal of Physics A General Physics, 2005, 39(8): 2006.

[13] ZHANG Z Z, ZHOU S G, FANG L J, et al. Maximal planar scale-free sierpinski networks with small-world effect and power-law strength-degree correlation [J]. EPL (Europhysics Letters)， 2007, 79(3): 417-429.

[14] LIU X, YAO B, ZHANG W J, et al. Uniformly bound-growing network models and their spanning trees [C]∥ International Conference on Information and Communications Technologies, 2014: 1-5.

[15] WANG X M, YAO B, MA F, et al. Hierarchical structure and particular spanning trees of edge-bound growing network models [C]∥International Conference on Fuzzy Systems and Knowledge Discovery, 2015:444-449.

[16] WANG X M, YAO B, MA F, et al. On composition and decomposition of networks [C]∥ International Conference on Biomedical Engineering and Informatics, 2015:783-788.

[17] WANG X M, ZHAO X Y, YAO B, et al. Algorithms for maximum leaf spanning tress of edge-growing network models in information system [J]. Applied Mechanics & Materials, 2015, 775: 431-435.

New method for cumulative distribution of scale-free network

WANGXiaomin1,YAOBing1，2

(1. College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China; 2. School of Electronics and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

By applying algorithm method, the maximal planar network with scale-free properties is employed. The cumulative degree distribution and edge-cumulative degree distribution are computed, and the equivalence between them is testified. Besides, the new statistical index, namely, the mix cumulative distribution between edge and vertex on the basis of different mixed method is provided. A conjecture: If the mixed mode is linear, the mix cumulative distribution is equivalent to cumulative distribution is proposed. This conjecture makes a contribution to discussing scale-free network by applying all-round and multi-angle standpoint.

scale-free network; vertex cumulative distribution; edge-cumulative distribution; power law distribution

10.13471/j.cnki.acta.snus.2017.03.007

2016-09-19 基金项目：国家自然科学基金(61163054, 61363060, 61662066)

王晓敏(1989年生)，女；研究方向：复杂网络；E-mail: 704944897@qq.com

姚兵(1956年生)，男；研究方向：图着色与标号、复杂网络；E-mail: yybb918@163.com

O157.5

A

0529-6579(2017)03-0041-05