两类Liénard系统的小振幅极限环*
熊峰,黄文韬,2
(1. 桂林电子科技大学数学与计算科学学院,广西 桂林 541004; 2. 桂林航天工业学院理学部,广西 桂林 541004)
两类Liénard系统的小振幅极限环*
熊峰1,黄文韬1,2
(1. 桂林电子科技大学数学与计算科学学院,广西 桂林 541004; 2. 桂林航天工业学院理学部,广西 桂林 541004)
Liénard系统;奇点量;细焦点;极限环
Liénard 系统是微分方程中一类经典的系统。Liénard方程最早被发现于20世纪20年代。1928年,法国数学家Liénard将其一般形式推广总结出来,有如下二阶微分方程形式:
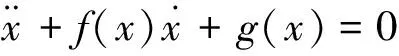
(1)
它有几类等价的微分方程组,其中一类有如下形式:
(2)
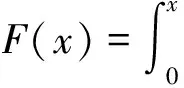

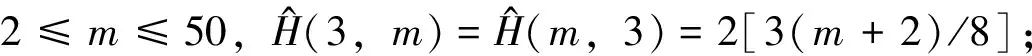
(3)
(4)
其中a2,a3,a4,a5,a6,a7,b3,b5,b6∈R,下面给出本文研究中需要的一些基础知识。
考虑如下实多项式系统
引理1[9-10]
(5)
通过变换

(6)
系统(5)被转化成下面的复系统
(7)
其中z,w,T是复变量,对于系统(7)可以逐项确定形式级数
(8)
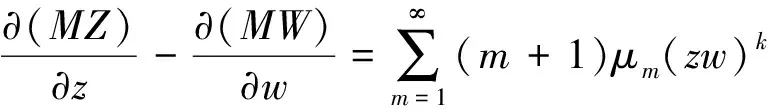
(9)
(10)
定义1 引理1中的μm称为系统(7)原点的第m个奇点量。若
则称原点为系统的k阶细奇点,如果所有的μk=0,则称原点为(7)的中心。归纳文[3-5]等的结论有如下结果。
引理2 对系统(5),其伴随复系统(7)原点的奇点量μi(i=1,…,k)有k个独立的参数θ=(θ1,…,θk),若θ=θ0时,系统(7)原点为k阶细奇点(相应地系统(5)的原点为k阶细焦点),且雅克比行列式满足
则系统(5)在原点的充分小邻域内可扰动出k个小振幅极限环。
1 系统(3)的奇点量与极限环
通过变换(6),系统(3)转化为其伴随复系统:
(11)
根据引理1的递推公式,经过仔细计算,得系统(11)原点的前九阶奇点量如下:
其中
F1= 490a2+ 2 646a6-2 205b3-8 82a2b5+
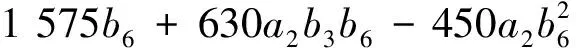
F2= -8 575 + 6 174a2-3 430a2b3+
15 435b5+ 4 900a2b6-11 025b3b6-4 410a2b5b6+
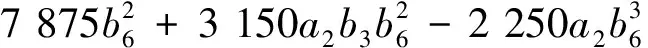
F3= 27 783 + 2 450a2-11 025b3-
4 410a2b5-7 875b6-2 268a2b6+
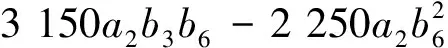
F4=-1 323-350a2+210a2b5+108a2b6,
76 919 220b5+ 138 454 596b6+
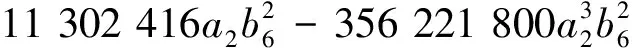
F6= 112 185 067 078 287 + 81 668 445 324 984a2+
定理1 对于系统(3)或者系统(11),原点均不是系统的中心。
证明 若原点是系统(11)的中心,则至少满足μi=0(i=1,…,9)成立。用Mathematica软件可算得μi的Groebner基,有
GroebnerBasis[(μ1,μ2,…,μ9),
从而得到μi(i=1,…,9)无公共实根,则μi不可能同时为0。证明完毕。
由奇点量表达式及定理1,经过仔细计算,有:
定理2 系统(11)的原点是9阶细奇点(相应的系统(3)的原点是9阶细焦点)当且仅当下列条件成立:
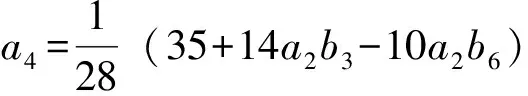
(12)
为了方便应用,取条件(12)的一组近似解如下:a2=-8.687 902 695 280 310 386 372 535 561→ ←267 497 861 887 667 656 914 8…
a3=0
a4=-7.819 112 425 752 279 347 735 282 005 → ←140 748 075 698 900 891 223 4…
a5=-3.475 161 078 112 124 154 549 014 224 → ←506 999 144 755 067 062 765 9…
a6=2.609 695 557 098 913 111 090 399 849 → ←304 541 527 966 817 539 057 8…
(13)
b3=2.332 203 415 494 509 727 338 816 257 094→ ←152 243 605 177 452 566 5…
b5=0.765 518 605 288 184 783 012 543 178 560→ ←337 250 998 721 644 575 5…
b6=0.342 225 757 741 530 933 853 094 928 710→ ←726 629 724 412 789 848 47…
定理3 对于系统(3),当系数满足条件(12)时,通过微扰在原点邻域可分支出九个极限环。
证明 由定理2知,原点是系统(3)的9阶细焦点。将系统(11)中奇点量表达式与式(13)代入雅克比行列式有:
0.007 957 122 583 684 067 743 343 108→
←392 562 154 328 468 624i≠0
(14)
由引理2知,系统(3)在原点的充分小邻域可分支出9个极限环。
2 系统(4)原点处的极限环
对复系统原点的奇点量进行计算,根据引理1,可算得复系统原点的前八阶奇点量。
定理4 对于系统(4)的伴随复系统,原点的前八阶奇点量为:
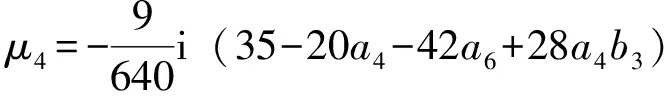
其中
与前述一致的讨论,我们有
定理5 系统(4)的伴随复系统原点是8阶细奇点(相应的系统(4)是8阶细焦点),当且仅当下列条件成立:
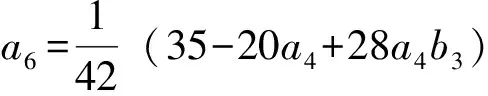
(15)
为了方便应用,取(15)式的一组近似解如下
a3=0,
a4=1.066 199 745 897 643 024 480 300 234→ ←879 325 174 247 617 416 339 2…
a5=0,
a6=2.499 999 999 999 999 999 999 999 999 → ←894 591 005 342 125 416 194…
a7=0.852 959 796 718 114 419 584 240 136→ ←842 496 399 959 665 416 154 5…
(16)
b3=3.059 062 112 534 832 064 433 729 022→ ←782 908 032 703 145 369 381 4…
b5=0.801 673 224 169 897 089 309 161 039→ ←794 232 564 336 279 331 615 5…
定理6 对于系统(4),当系数满足式(16)时,通过微扰在原点邻域可分支出八个极限环。
证明 由定理5知当式(16)成立时,原点是系统(4)的8阶细焦点,将式(16)以及定理5中的奇点量表达式代入雅克比行列式
0.007 957 122 583 684 067 743 343 102→
←619 368 852 012 419 584 579 936i≠0
(17)
由引理2知,系统(4)在原点邻域可分支出8个极限环。
[1] CHRISTOPHER C, LYNCH S. Small-amplitude limit cycle bifurcations for Lienard systems with quadratic or cubic damping or restoring forces [J]. Nonlinearity, 1999, 12(4):1099-1112.
[2] YU P, HAN M. Limit cycles in generalized Lienard systems [J]. Chaos Solitons Fractal, 2006, 30(5): 1048-1068.
[3] YU P, HAN M. Twelve limit cycles in a cubic case of the 16th Hilbert problem [J]. Int J Bifurcation Chaos, 2005,15(7): 2191-2205.
[4] LI J, LIU Y. New results on the study of Zq-Equivariant planar polynomial vector fields [J]. Qualitative Theory of Dynamical Systems, 2010, 9(1):167-219.
[5] YU P, CORLESS R. Symbolic computation of limit cycles associated with Hilbert’s 16th problem [J]. Comm Non Sci Num Simu, 2009,14(12): 4041-4056.
[6] 陈树辉,黄武林,徐兆. Liénard 方程半稳定极限环的计算[J]. 中山大学学报(自然科学版),1998, 37(6): 5-9. CHEN S H, HUANG W L, XU Z. Calculation of semi-stable limit cycles of Liénard equation [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 1998, 37(6): 5-9.
[7] 李时敏. 一类不连续广义Liénard 微分系统的极限环分支[J]. 中山大学学报(自然科学版),2015, 54(5): 15-18. LI S M. Bifurcation of limit cycles for a class of discontinuous generalized liénard differential system [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2015, 54(5): 15-18.
[8] 胡军胜. 一类三次Liénard方程的极限环分析[J]. 中山大学学报(自然科学版),2000,39(S3): 18-20. HU J S. Limit cycles analysis to a class of cubic Liénard equations [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2000, 39(S3): 18-20.
[9] 刘一戎,陈海波. 奇点量公式的机器推导与一类三次系统的前10个鞍点量[J]. 应用数学学报,2002, 25(2): 295-302. LIU Y R, CHEN H B. Formulas of singular point quantities and the first 10 saddle quantities for a class of cubic system [J]. Acta Mathematicae Applicatae Sinica, 2002, 25(2): 295-302.
[10] 刘一戎,李继彬. 论复自治微分系统的奇点量[J]. 中国科学(A辑), 1989(3): 245-255. LIU Y R, LI J B. Theory of values of singular point in complex autonomous differential systems [J]. Science in China (Series A), 1989(3): 245-255.
Small amplitude limit cycles for two classes of Liénard systems
XIONGFeng1,HUANGWentao1,2
(1. School of Mathematics and Computational Science, Guilin University of Electronic Technology, Guilin 541004, China; 2. School of Science, Guilin University of Aerospace Technology, Guilin 541004, China)
Liénard system; singular point; fine focus; limit cycles
10.13471/j.cnki.acta.snus.2017.03.010
2016-08-05 基金项目:国家自然科学基金 (11261013,11361017);广西省自然科学基金重点项目(2016GXNSFDA380031)
熊峰(1990年生),男;研究方向:微分方程定性理论及其应用;E-mail:1073620114@qq.com
黄文韬(1966年生),男;研究方向:微分方程定性理论及其应用;E-mail: huangwentao@163.com
O
A
0529-6579(2017)03-0066-05

