基于非标准Lagrange函数的动力学系统的Noether-Mei对称性与守恒量*
宋静, 张毅
(1.苏州科技大学数理学院, 江苏 苏州 215009; 2.苏州科技大学土木工程学院, 江苏 苏州 215011)
基于非标准Lagrange函数的动力学系统的Noether-Mei对称性与守恒量*
宋静1, 张毅2
(1.苏州科技大学数理学院, 江苏 苏州 215009; 2.苏州科技大学土木工程学院, 江苏 苏州 215011)
研究基于两类非标准Lagrange函数(指数Lagrange函数和Lagrange幂函数)的动力学系统的Noether-Mei对称性及其守恒量。首先,给出基于指数Lagrange函数和Lagrange幂函数的动力学系统的Noether-Mei对称性的定义与判据;其次,提出由系统的Noether-Mei对称性导致的Noether守恒量与Mei守恒量的存在条件及其形式,给出四个Noether-Mei对称性定理。最后,举例说明结果的应用。
非标准Lagrange函数;Noether-Mei对称性;Noether守恒量;Mei守恒量
动力学系统的对称性与守恒量因其具有重要的数学意义与物理意义,现已成为分析力学一个活跃的研究方向,并在现代数学、力学、物理学中占有及其重要的地位。力学系统的对称性主要有Noether对称性、Lie对称性和Mei对称性,相应的守恒量主要有Noether守恒量、Hojman守恒量和Mei守恒量[1-6]。随着研究的深入,诸多学者对两种以上对称性进行了研究,并已取得一些成果[7-11]。非标准Lagrange函数,又称非自然Lagrange函数,不同于经典的Lagrange函数,它没有动能与势能的明显区分。近年来,对于基于非标准Lagrange函数的动力学系统的研究已经取得一系列成果。Musielak[12-13]研究了耗散系统中获得非标准Lagrange函数的方法及其存在条件,El-Nabulsi[14-15]研究了非线性动力学系统基于两类非标准Lagrange函数的作用量及动力学方程,并将非标准Lagrange函数应用于Friedmann-Robertson-Walker时空中,讨论了非标准Lagrange函数在宇宙学中的影响。张毅等[16-17]研究了基于非标准Lagrange函数的动力学系统的Noether对称性和降阶法。本文研究基于非标准Lagrange函数的动力学系统的Noether-Mei对称性与守恒量,给出系统的Noether-Mei对称性的定义和判据,建立Noether-Mei对称性与Noether守恒量,Mei守恒量之间的联系,给出了四个Noether-Mei对称性定理,并结合具体算例说明了结果的应用。
1 基于指数Lagrange函数的Noether- Mei对称性与守恒量
1.1 Noether-Mei对称性
基于指数Lagrange函数的动力学系统的运动微分方程为[16]
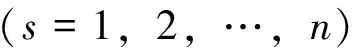
(1)
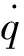
定义1 对于基于指数Lagrange函数的动力学系统(1),如果一个对称性既是Noether对称性又是Mei对称性,则称这个对称性为该系统的Noether-Mei对称性。
取时间t与广义坐标qs的无限小变换
(2)
其展开式为
(3)
其中ε为无限小参数,ξ0,ξs为无限小变换的生成元。
假设在无限小变换(2)下,指数Lagrange函数exp(L)变换为
(4)
其中
(5)
如果无限小变换(2)的生成元ξ0和ξs满足方程
(6)
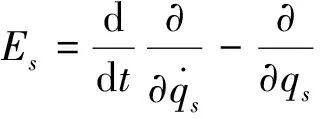
(7)
则相应的对称性为基于指数Lagrange函数的Noether对称性。于是有
(8)
则相应的对称性为基于指数Lagrange函数的动力学系统的Noether-Mei对称性。
1.2Noether-Mei对称性导致的守恒量
定理1 对于基于指数Lagrange函数的动力学系统(1),Noether-Mei对称性可导致Noether守恒量,形如
(9)

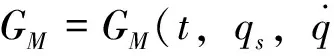
(10)
则系统的Noether-Mei对称性导致Mei守恒量,形如
(11)
证明
1.3 算例
已知某指数Lagrange函数为[16]
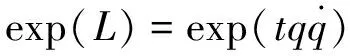
(12)
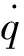
系统的运动微分方程为
(13)
由式(5)可得
(14)
取无限小生成元
(15)
则有
(16)
由式(12)容易验证生成元(15)满足Mei对称性的确定方程(6),故生成元(15)相应于系统的Mei对称性。由Noether等式(7)得
(17)
将生成元(15)代入式(17),得
GN=0
(18)
则生成元(15)相应于系统的Noether对称性。因此,生成元(15)是基于指数Lagrange函数的动力学系统的Noether-Mei对称性。据此给出与生成元(15)相应的Mei对称性结构方程
(19)
其中
(20)
由方程(19)和(20)得
GM=0
(21)
由定理2,系统存在Mei守恒量
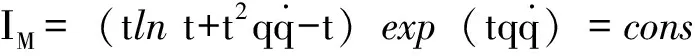
(22)
式(22)是由基于指数Lagrange函数的动力学系统的Noether-Mei对称性导致的Mei守恒量。再将生成元(15)和规范函数(18)代入式(9),得到Noether守恒量
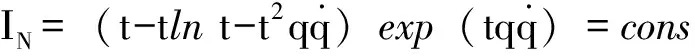
(23)
式(23)是由基于指数Lagrange函数的动力学系统的Noether-Mei对称性导致的Noether守恒量。
2 基于Lagrange幂函数的Noether- Mei对称性与守恒量
2.1 Noether-Mei对称性
基于Lagrange幂函数的动力学系统的运动微分方程为[16]
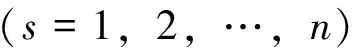
(24)
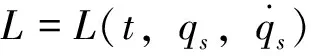
定义2 对于基于Lagrange幂函数的动力学系统(24),如果一个对称性既是Noether对称性又是Mei对称性,则称这个对称性为该系统的Noether-Mei对称性。
假设在无限小变换(2)下,Lagrange幂函数L1+α变换为
(25)
如果无限小变换(2)的生成元ξ0和ξs满足方程
(26)
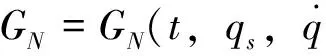
(27)
则相应的对称性为基于Lagrange幂函数的Noether对称性。于是有
(28)
则相应的对称性为基于Lagrange幂函数的动力学系统的Noether-Mei对称性。
2.2Noether-Mei对称性导致的守恒量
定理3 对于基于Lagrange幂函数的动力学系统(24),Noether-Mei对称性可导致Noether守恒量,形如
(29)

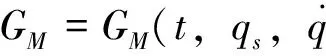
(30)
则系统的Noether-Mei对称性导致Mei守恒量,形如
(31)
证明
2.3 算例
已知某Lagrange幂函数为
(32)
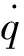
取α=1时,系统的运动微分方程为
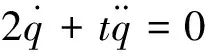
(33)
由式(5)可得
(34)
取无限小生成元
(35)
则有
(36)
由式(33)容易验证生成元(35)满足Mei对称性的确定方程(26),故生成元(35)相应于系统的Mei对称性。由Noether等式(27)得
(37)
将生成元(35)代入式(37),得
GN=0
(38)
则生成元(35)相应于系统的Noether对称性。因此,生成元(35)是基于Lagrange幂函数的动力学系统的Noether-Mei对称性。据此给出与生成元(35)相应的Mei对称性的结构方程
(39)
其中
(40)
由方程(39)和式(40)得
GM=0
(41)
由定理4,系统存在Mei守恒量
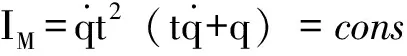
(42)
式(42)是由基于Lagrange幂函数的动力学系统的Noether-Mei对称性(35)导致的Mei守恒量。将生成元(35)和规范函数(38)代入式(29),得到Noether守恒量
(43)
式(43)是由基于Lagrange幂函数的动力学系统的Noether-Mei对称性导致的Noether守恒量。
3 结 论
本文给出了基于非标准Lagrange函数的动力学系统的Noether-Mei对称性,它既是系统的Noether对称性又是Mei对称性。由Noether-Mei对称性可以得到Noether守恒量和Mei守恒量。文中基于非标准Lagrange函数的动力学系统的Noether-Mei对称性推导出四个关于Noether守恒量和Mei守恒量的定理。本文的方法与结果具有普遍意义,可以推广到其他约束力学系统。
[1] 梅凤翔. 李群李代数对约束力学系统的应用[M]. 北京: 科学出版社, 1999.
[2] 梅凤翔. 约束力学系统的对称性与守恒量[M]. 北京: 北京理工大学出版社, 2004.
[4] HOJMAN S A. A new conservation law constructed without using either Lagrangians or Hamiltonians[J]. Journal of Physics A: Mathematical and General, 1992, 25: 291-295.
[5] 王树勇,梅凤翔. 相空间中完整约束系统的形式不变性[J]. 中山大学学报(自然科学版), 2002, 41(6): 10-13. WANG S Y, MEI F X. Form invariance of holonomic systems in phase space[J]. Acta Scientiraum Naturalium Universitatis Sunyatseni, 2002, 41(6): 10-13.
[6] 张毅. 相空间中类分数阶变分问题的Noether对称性与守恒量[J]. 中山大学学报(自然科学版), 2013, 52(4): 45-50. ZHANG Y. Noether symmetry and conserved quantity for a fractional action-like variational problem in phase space[J]. Acta Scientiraum Naturalium Universitatis Sunyatseni, 2013, 52(4): 45-50.
[7] 方建会,丁宁,王鹏. 非完整力学系统的Noether-Lie对称性[J]. 物理学报, 2006, 55(8): 3817-3820. FANG J H, DING N, WANG P. Noether-Lie symmetry of nonholonomic mechanical system[J]. Acta Physica Sinica, 2006, 55(8): 3817-3820.
[8] 刘仰魁, 方建会. 相空间中变质量力学系统Lie-Mei对称性的两个守恒量[J]. 物理学报, 2008, 57(11): 6699-6703. LIU Y K, FANG J H. Two types of conserved quantities of Lie-Mei symmetry for a variable mass system in phase system[J]. Acta Physica Sinica, 2008, 57(11): 6699-6703.
[9] 王雪萍, 张毅. Birkhoff系统的Noether-Mei对称性与守恒量[J]. 中山大学学报(自然科学版), 2016, 55(4): 53-55. WANG X P, ZHANG Y. Noether-Mei symmetry and conserved quantity of Birkhoffian system[J]. Acta Scientiraum Naturalium Universitatis Sunyatseni, 2016, 55(4): 53-55.
[10] FANG J H, LIU Y K, ZHANG X N. New conserved quantities of Noether-Mei symmetry of mechanical system in phase space[J]. Chinese Physics B, 2008, 17(6): 1962-1966.
[11] XIE Y L, JIA L Q. Special Lie-Mei symmetry and conserved quantities of Appell equations expressed by Appell function. Chinese Physics Letters, 2010, 27(12): 120201.
[12] MUSIELAK Z E. Standard and non-standard Lagrangians for dissipative dynamical systems with variable coefficients [J]. Journal of Physics A: Mathematical and Theoretical, 2008, 41(5): 295-302.
[13] MUSIELAK Z E. General conditions for the existence of non-standard Lagrangians for dissipative dynamical systems [J]. Chaos, Solitons and Fractals, 2009, 42(5): 2645-2652.
[14] EL-NABULSI R A. Non-linear dynamics with non-standard Lagrangians [J]. Qualitative Theory of Dynamical Systems, 2013, 12(2): 273-291.
[15] EL-NABULSI R A. Nonstandard Lagrangian cosmology[J]. Journal of Theoretical and Applied Physics, 2013, 7(1): 1-12.
[16] ZHANG Y, ZHOU X S. Noether theorem and its inverse for nonlinear dynamical systems with nonstandard Lagrangians[J]. Nonlinear Dynamics, 2016, 84(4): 1867-1876.
[17] 周小三, 张毅. 基于非标准Lagrange函数的动力学系统的Routh降阶法[J]. 力学季刊, 2016, 37(1): 15-20. ZHOU X S, ZHANG Y. Routh Method of reduction for dynamical systems with non-standard Lagrangians[J]. Chinese Quarterly of Mechanics, 2016, 37(1): 15-20.
Noether-Mei symmetry and conserved quantity for dynamical systems with non-standard Lagrangians
SONGJing1,ZHANGYi2
(1.College of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China; 2.College of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, China)
This paper focuses on studying the Noether-Mei symmetry and the conserved quantity for dynamical systems with non-standard Lagrangians (exponential Lagrangians and power law Lagrangians). Firstly, The definition and the criteria of Noether-Mei symmetry for dynamical systems with non-standard Lagrangians are given. Secondly, The conditions that Noether-Mei symmetry leads to Noether conserved quantity or Mei conserved quantity and the form of conserved quantities are put forward. And four theorems for Noether-Mei symmetry and conserved quantities are established. Two examples are given to illustrate the application of the results.
non-standrad Lagrangian; Noether-Mei symmetry; Noether conserved quantity; Mei conserved quantity
10.13471/j.cnki.acta.snus.2017.03.004
2016-10-08 基金项目: 国家自然科学基金(11272227,11572212);苏州科技大学研究生科研创新计划(SKYCX16_12)
宋静(1992年生),女;研究方向:力学中的数学方法;E-mail: sandyquiet@hotmail.com
张毅(1964年生),男;研究方向:动力学与控制;E-mail: zhy@mail.usts.edu.cn
O316
A
0529-6579(2017)03-0026-05

