雷达点元聚类算法性能的比较与分析

余渝生， 王志诚

（上海无线电设备研究所，上海200090）

0 引言

在高分辨雷达体制下，真实目标的雷达回波将覆盖多个距离-多普勒分辨单元，形成若干雷达点元。若以点元为单位进行目标检测和识别，则会将真实目标识别为多个目标。因此，需要对检测到的所有点元进行聚类。点元聚类是指将所有检测到的属于一个真实目标的雷达点元进行归类的操作。雷达点元聚类不仅有助于降低检测虚警概率，同时有助于真实目标的识别以及目标跟踪点的选取。点元聚类应同时具有完备性和排他性，即在将所有属于同一目标的点元归为一类的同时，将不属于该目标的点元排除。本文主要介绍了三种点元聚类常用的算法：圆心半径聚类算法、边缘聚类算法和逐点聚类算法，并对这三种算法的聚类效果以及聚类时间进行了比较。

1 圆心半径聚类算法

圆心半径聚类算法是一种较简单的聚类算法，该算法将雷达目标视为一个圆，以其圆心和半径进行聚类。如图1所示，假设目标T 中被设为圆心的点元A 在距离 -多普勒二维检测平面（简称：检测平面，下同）内的坐标为（xA，yA），某个待聚类的点元B在检测平面内的坐标为（xB，yB），再假设目标T 的半径为R。若点元A 与点元B之间的距离满足关系式：

则点元B属于目标T。

图1 圆心半径聚类算法原理示意图

在实际处理中，圆心半径聚类算法通常将雷达回波能量最大的点元作为圆心进行点元聚类。因此，需要将所有点元按照能量大小进行排序。然后按照能量从大到小的顺序对剩下的点元进行聚类。圆心半径聚类算法的具体流程：

a）对所有点元按能量大小排序；

b）以未被聚类的能量最大的点元为圆心，以预期目标最大尺寸的一半为聚类半径；

c）遍历剩下的点元，查询这些点元与圆心之间的距离是否满足式（1），若满足则将其与圆心归为一类，同时更新该类的属性；

d）重复b）、c）两个步骤，直到检测平面内的所有点元都被聚类。

圆心半径聚类算法的优点是原理简单，易于实施。但该算法存在聚类半径不可调，聚类形状单一以及无法边检测边聚类等缺点，无法完成复杂目标的聚类处理。

2 边缘聚类算法

边缘聚类算法是基于圆心半径聚类算法的改进算法。该算法以当前类属的边缘为基准进行聚类，随着聚类点元的增加，当前类属的边缘会不断向外扩展，能够有效地对复杂目标聚类。在实际操作中，当前类属的边缘由四个边缘点表示，边缘点的坐标分别由该类属中的所有点元在距离维和频率维上的最大值和最小值组成，分别为（xmin，ymin）、（xmax，ymin）、（xmin，ymax）、（xmax，ymax）。边缘聚类算法具备边检测边聚类的能力，无需等待点元检测操作完成，聚类效率较高。图2给出了边缘聚类算法的示意图。

图2 边缘聚类算法原理示意图

图2 中，虚线框表示当前的聚类范围，E1、E2、E3和E4表示类属范围的边缘点。待聚类的点元分别计算与这四个类属边缘点之间的距离。若任意一段距离小于等于设定门限，则待聚类点元属于当前类属。若该点元被聚类入当前的类属，则立即对当前类属的边缘点进行更新，为下一次聚类做准备。

边缘聚类算法的具体流程：

a）从检测平面中检测出一个新的待聚类的点元；

b）判断当前是否有类属可以进行聚类，若当前没有类属，则生成一个类属，并对该类属进行初始化，将该类边缘的四个点的坐标置为该点元的坐标，然后进行下一个点元的检测；

c）若当前有类属，则将待聚类点元与当前所有类属的边缘进行逐一比较，若满足聚类条件，则将该点元归为某个类属，若该点元在聚类为某个类属的同时已经具有自己的类属，且两个类属不相同，那么将这两个类属合并为一个类属；

d）若待聚类点元不属于当前任何类属，则生成一个新类，并对该类进行初始化，将该类边缘的四个点的坐标置为该点元的坐标；

e）重复以上四个步骤，直到整个检测平面遍历结束。

3 逐点聚类算法

圆心半径聚类算法和边缘聚类算法都是以待聚类点元与参考点之间的聚类为依据进行聚类的。与这两类算法不同，逐点聚类算法是以待聚类点周边其它点元的类属情况为依据进行聚类的，即对待聚类点元周边一定区域内的点元的类属情况进行查询。查询的范围和数量决定了聚类的范围和形状，聚类灵活性高。

逐点聚类算法需遍历查询待聚类点元周边指定区域和数量的点元的类属情况，并以此为依据对待聚类点元的类属进行判定。

如图3所示，原点o 上的空心点为待聚类点元，实心点为待查询的点元。算法对实心点的类属情况进行遍历查询。根据查询结果，分三种情况对待聚类点元的类属进行判定。分别以该点的坐标为基准，去查询其周围的规定范围的点的类属，每查询一个点，进行一次处理。

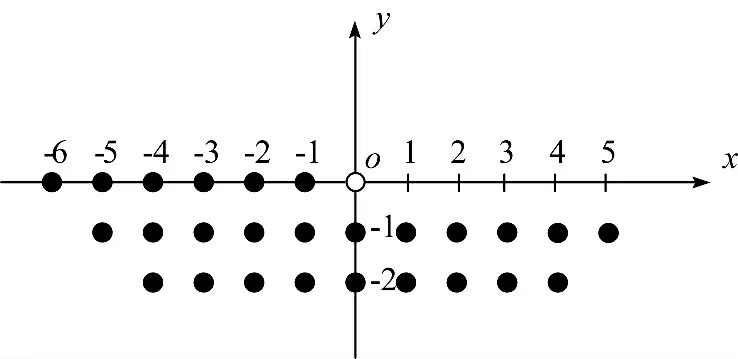
图3 逐点聚类算法原理示意图

（1）当前查询点无任何类属

若当前查询点无任何类属，则算法不进行任何操作，直接查询下一个点。

（2）当前查询点具有类属

若当前查询点有类属，则算法根据待聚类点元的类属情况，进行聚类操作。若待聚类点元没有类属，则将当前查询点的类属赋予待聚类点元；若待聚类点元有类属，但与查询点的类属不同，则将查询点的类属赋予待聚类点元所在类属的所有点；若待聚类点元与查询点元的类属相同，则不进行任何操作，直接查询下一个点。

（3）所有查询点均无类属

若查询的所有点都无类属，则算法将待聚类点元设为一个新的类属。

4 三种聚类算法的仿真与比较

采用模拟回波数据和真实回波数据分别对三种聚类算法进行验证。从聚类效果和聚类时间两个方面进行比较和评估。

4.1 模拟回波数据验证

利用模拟回波数据，在三种仿真状态下对聚类算法进行验证。对三种算法在软件优化和未优化两种情况下的聚类效果和聚类时间进行了对比。每种状态均包含100个点元，由此形成的目标个数在三种状态下分别为2 个、3 个和5 个。表1列出了三种仿真状态下的模拟回波数据规格。

表1 三种仿真状态下的模拟回波数据规格

（1）仿真状态Ⅰ

仿真状态Ⅰ包含2个目标，分别包含96个点元和4个点元。图4给出了仿真状态Ⅰ的模拟回波数据示意图。表2列出了三种聚类算法对该仿真状态Ⅰ中点元的聚类结果。

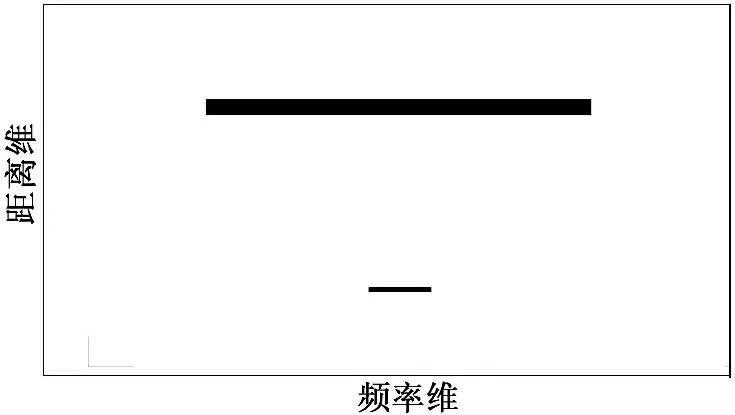
图4 仿真状态Ⅰ模拟回波数据示意图

在仿真状态Ⅰ下，圆心半径聚类算法将较大的目标聚类为几个小目标，聚类效果不理想；而边缘聚类算法和逐点聚类算法能够有效地聚类。从表2 中可以看出，逐点聚类算法的聚类时间较长。

表2 三种聚类算法对仿真状态Ⅰ的聚类结果

（2）仿真状态Ⅱ

仿真状态Ⅱ包含3个目标，其中2个目标各包含48个点元，一个目标包含4个点元。图5给出了仿真状态Ⅱ的模拟回波数据示意图。

表3列出了三种聚类算法对该仿真状态Ⅱ中点元的聚类结果。

在仿真状态Ⅱ下，圆心半径聚类算法仍将大的目标聚类为多个小目标，效果仍不理想。边缘聚类算法和逐点聚类算法仍能够有效地聚类，但逐点聚类算法的聚类时间仍较长。

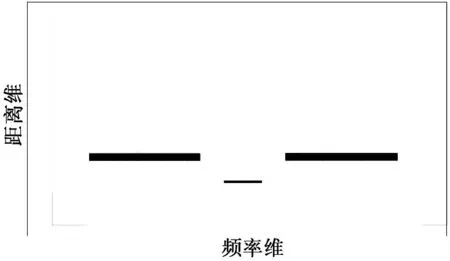
图5 仿真状态Ⅱ模拟回波数据示意图

表3 三种聚类算法对仿真状态Ⅱ的聚类结果

（3）仿真状态Ⅲ

仿真状态Ⅲ包含5个目标，其中4个目标各包含24个点元，一个目标包含4个点元。图6给出了仿真状态Ⅲ的模拟回波数据示意图。

表4列出了三种聚类算法对该仿真状态Ⅲ中点元的聚类结果。

图6 仿真状态Ⅲ模拟回波数据示意图

表4 三种聚类算法对仿真状态Ⅲ的聚类结果

在仿真状态Ⅲ下，随着目标中点元数量的减少，圆心半径聚类算法的聚类效果变好，且聚类时间与边缘聚类算法相当。另外，边缘聚类算法和逐点聚类算法仍能够有效地聚类，其中逐点聚类算法的聚类时间仍较长。

通过对以上三种仿真状态的验证发现，圆心半径聚类算法对于点元数量较多的目标不能够有效地聚类，而当目标所包含的点元数量减小到一定范围后，聚类效果变好。边缘聚类算法和逐点聚类算法均能有效聚类。在聚类时间方面，三种仿真状态下，边缘算法的聚类时间最短，圆心半径聚类算法次之，逐点聚类算法最长。因此，逐点聚类算法不适于对实时性要求高的系统。

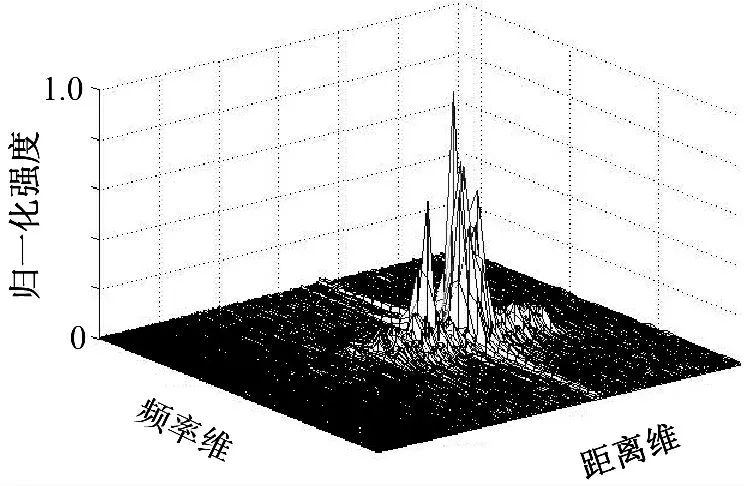
图7 真实回波数据平面三维视图

4.2 真实回波数据验证

采用真实雷达回波数据对三种聚类算法进行仿真。该数据为某型号雷达在进行抗箔条试验时所采集的舰船和箔条的回波数据。图7、图8 给出了该数据的“频率-距离-强度”三维视图以及“频率-距离”平面视图。

从图7、图8中可以看出，数据中含有两个目标。通过对该数据进行恒虚警检测，得到20个点元。其中，箔条目标包含18个点元；舰船目标包含2个点元。在验证时，将圆心半径聚类算法的聚类半径设为10个点元；将边缘聚类算法的距离门限设为10个点元；将逐点聚类算法的查询点总数设为26点。下面给出三种聚类算法的聚类结果。

图8 真实回波数据俯视图

通过表5可以看出，三种聚类算法均能有效地聚类。其中，圆心半径聚类算法和边缘聚类算法的聚类时间相当，而逐点聚类算法的聚类时间则要长于前两种聚类算法。

表5 三种算法对雷达回波数据的聚类结果

5 总结

点元聚类算法是高分辨雷达信号处理的一个重要的组成部分，较好地对检测平面内所检测到的点元进行聚类是目标搜索跟踪、目标识别以及抗干扰等处理的前提。通过以上的分析和对比发现，圆心半径聚类算法由于其聚类半径不能够自适应地改变，不适于大型复杂目标的聚类；逐点聚类算法能够对复杂目标进行有效聚类，但其聚类时间较长，对系统的实时性影响较大；边缘聚类算法能够在较短的时间内完成对复杂目标的聚类，聚类效果较好。

［1］ William K.Pratt.数字图像处理（原书第三版）［M］.北京：机械工业出版社，2005.

［2］ 章毓晋.图像处理和分析［M］.北京：清华大学出版社，1999.［3］ 赵荣椿.数字图像处理导论［M］.西安：西北工业大学出版社，1995.

［4］ 刘书明，罗勇江.ADSP TS20XS系列DSP原理与应用设计［M］.北京：电子工业出版社，2007.

［5］ 郑存红，张文艳，董静.红外小目标聚类算法研究及DSP实现［C］.电子技术学术委员会，2006.