相控阵天线波束指向误差的线性插值补偿法

李毓琦， 牟成虎， 周 焯， 唐文明

（上海无线电设备研究所，上海200090）

0 引言

相控阵雷达以其灵活的空域处理能力提高了现代雷达的功能和性能。不同于机械扫描雷达，相控阵天线不能通过位置传感器获取波束扫描位置角度，波束指向必须精确设计。在精确制导雷达中，对相控阵天线波束指向误差应进行补偿。

文献［1］给出了天线单元的幅度和相位误差引起的波束指向误差的计算式，文献［2］给出了天线单元之间相位误差为相互独立的随机变量时波束指向误差的计算式，但没有给出波束指向误差的补偿方法。文献［3］与文献［4］分别采用“二可能值法”与“预加相位法”改善相控阵天线波束指向精度，它们都是基于改善移相器相位的方法控制波束指向误差。工程中，通常采用6位甚至更高位数的移相器，移相器相位控制误差不是造成波束指向误差的主要因素。辐射单元方向图差异、单元之间的互耦引起的幅相误差对波束指向误差有更大的影响。

本文针对弹载相控阵天线实测波束指向误差，在波束指向空域内进行分区处理。在每个分区内，可以认为天线波束指向误差呈线性，可以利用线性插值法进行波束指向误差的补偿修正。

1 相控阵天线波束的指向误差

影响相控阵天线波束指向误差的几种主要因素：

a）天线阵元加工和安装误差导致单元方向图的差异，从而引起的阵面幅相误差；

b）由辐射单元位置误差引起的阵面幅相误差［5］；

c）由移相器的量化误差和执行误差引起的阵面相位误差；

d）由衰减器量化误差和执行误差引起的阵面幅度误差，以及调整衰减器时附加调相引起的阵面相位误差；

e）阵元之间互耦引起的阵面幅相误差；

f）阵面温度不平衡引起的幅相误差。

考虑上述因素，阵面总相位均方根误差为

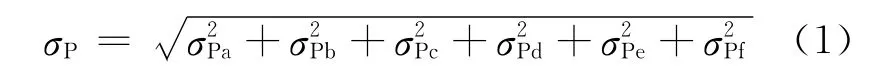
式中：σPa为单元方向图差异引起的相位均方根误差；σPb为单元安装位置引起的相位均方根误差；σPc为移相器相位均方根误差；σPd为衰减器相位均方根误差；σPe为单元互耦引起的相位均方根误差；σPf为阵面温度差异引起的相位均方根误差。阵面总幅度均方根误差为

采用SPSS 21.0软件进行统计分析，其中手术指标等计量资料用（±s）表示，采用 t检验，临床疗效等计数资料用[n(%)]表示，采用χ2卡方检验，P＜0.05为差异有统计学意义。

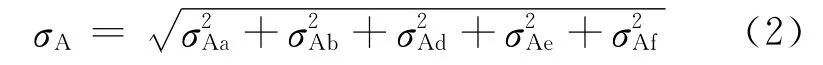
式中：σAa为单元方向图差异引起的幅度均方根误差；σAb为移相器幅度均方根误差；σAd为衰减器幅度均方根误差；σAe为单元互耦引起的幅度均方根误差；σAf为阵面温度不平衡引起的幅度均方根误差。文献［1］给出了法线方向波束指向误差与阵面辐射单元幅度、相位误差之间的关系

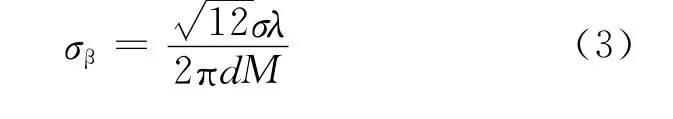
其中：

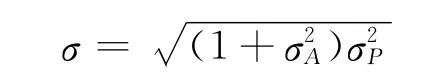
式中：λ为波长；d 为辐射单元之间的距离；M 为天线单元数量。由于不能精确估计天线单元之间耦合对阵面幅度、相位分布的影响，也不能精确测量每个天线单元方向图之间的差异进行补偿，相控阵天线实际的波束指向误差往往超过理论值。工程中，只能根据相控阵天线波束指向的实测误差进行补偿修正。

波束指向误差有两种补偿途径：一是通过校正阵面相位分布进行波束指向误差补偿；二是建立理论指向与实际指向之间的映射表，通过查表进行波束指向误差补偿。两种方法都需要大量的波束指向误差的测试数据。对于一个采用6位移相器的500个阵元的相控阵天线，设波束跃度为0.1°，二维扫描范围均为-60°～+60°，则在10个工作频点中需要进行约14.4×106个波位的测试。两种方法的存储量分别为43 Gbit和316 Mbit，工程上难以实现。线性插值补偿法是一种优化的映射查表补偿法，可以有效减小相控阵天线波束测试工作量，并降低存储量。

2 线性插值补偿法的基本原理

所谓插值，就是利用已知数据的数值来预测重构未知数据的过程。线性插值就是以折线来逼近曲线。为了计算y＝f（x）的函数值，把函数划分为n个区间，自变量x 在区间端点的值为x1，x2，…，xi，xi+1，…，xn，区间端点对应的准确值为y1，y2，…，yi，yi+1，…，yn。求函数值yc时（设xi＜xc＜xi+1），用点（xi，yi）和（xi+1，yi+1）连成的直线代替原函数，如图1所示。

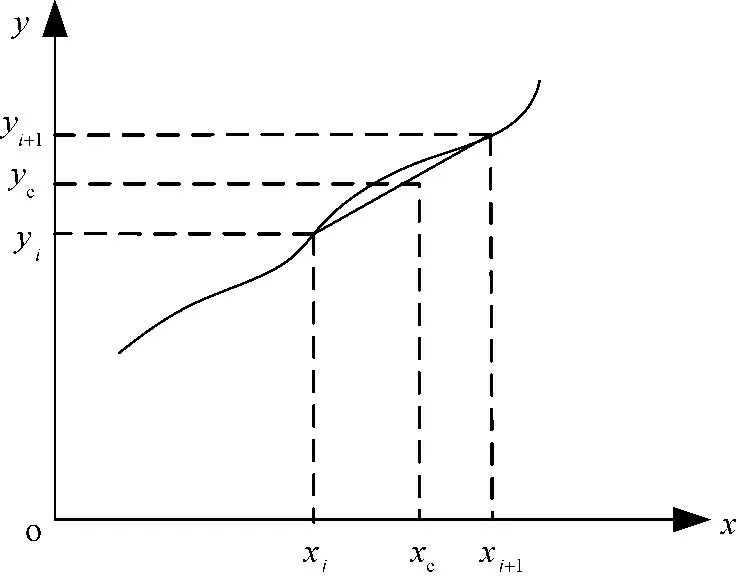
图1 线性插值图

函数值yc的计算公式为

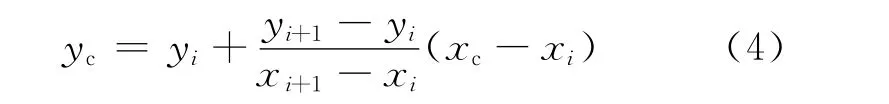
3 波束指向误差线性插值补偿方法

将相控阵天线波束指向范围按照与阵面平行的矩形区域进行均匀空间分割，如图2（a）所示。当划分的空域范围较小时，可认为该区域内波束指向误差分解至方位向和俯仰向的误差近似呈线性变化。于是，可以根据该区域边缘四个波位指向误差的测试值，近似计算得到区域内部任意波位的波束指向误差，并以此进行波束指向误差的补偿。天线阵面布局如图2（b）所示，yoz 为天线阵平面。波束指向角度坐标关系如图2（c）所示，θ为俯仰角，φ 为方位角。以图2（a）中的阴影区域为例，假设四个边缘波位“●”方位向和俯仰向的理论指向和实测指向分别如图3（a）与图3（b）所示。图中：（φ，θ）为理论值；（＾φ，＾θ）为实测值；“○”为需要插值计算的波位。

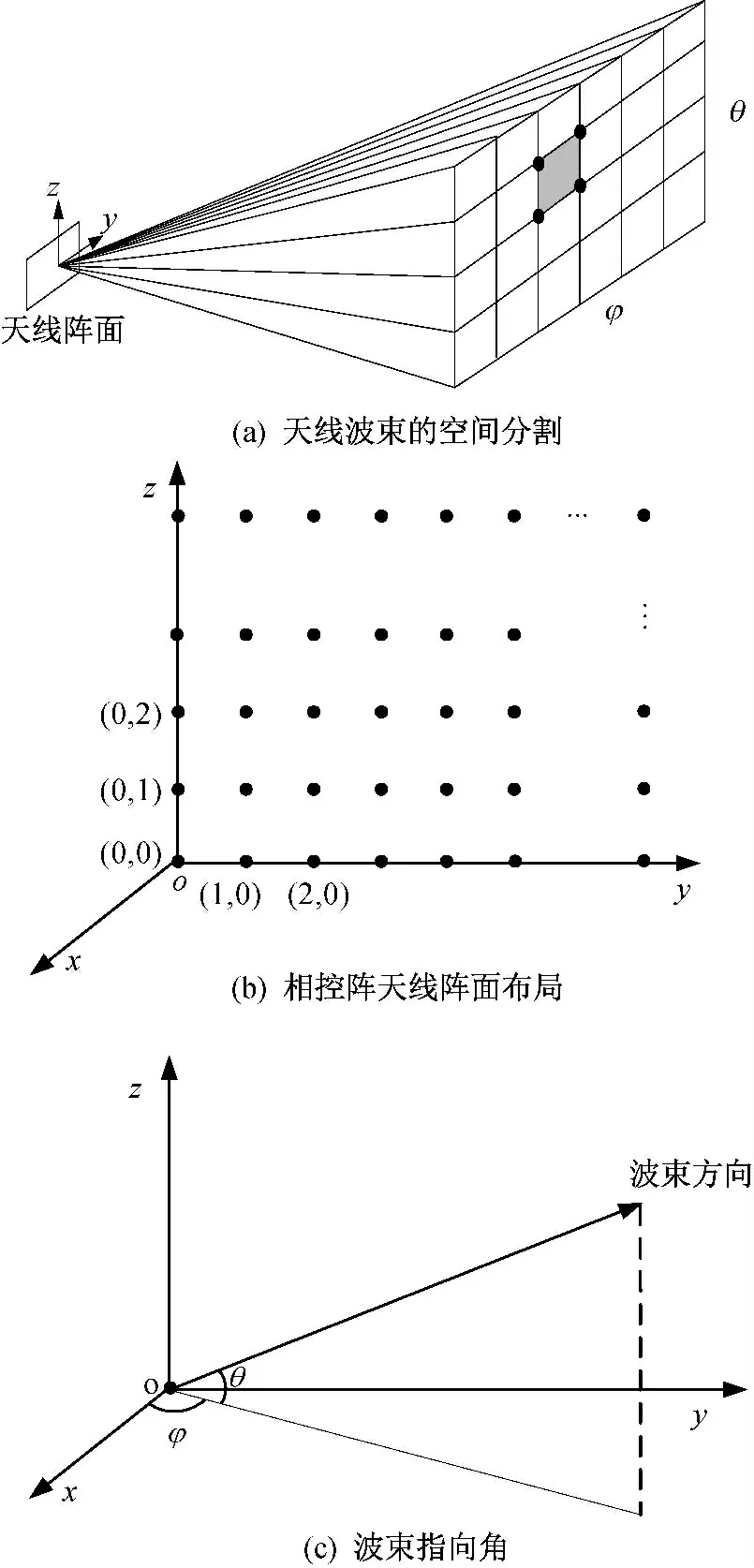
图2 天线波束的空间分割、阵面布局与波束指向角示意图

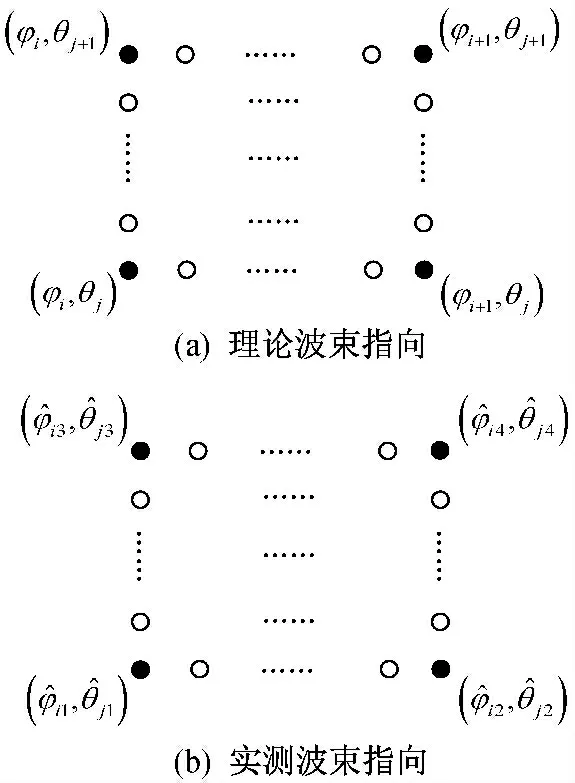
图3 波束指向情况

空间子区域四个边缘波位的方位指向误差为

四个边缘波位的俯仰指向误差为

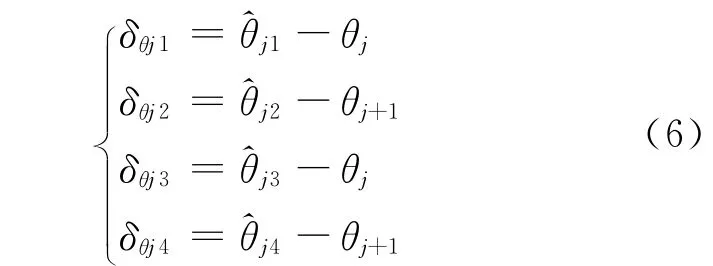
由于波束指向误差在四个波位各不相同，导致四个位置可能不在一个平面内（三点决定一个平面），因此将四个波位内的波束指向区域划分为两个平面，如图4所示。每个平面内的波束指向角的斜率可分解为方位方向斜率和俯仰方向斜率。然后，采用线性插值法近似计算区域内任意波位的波束指向误差。

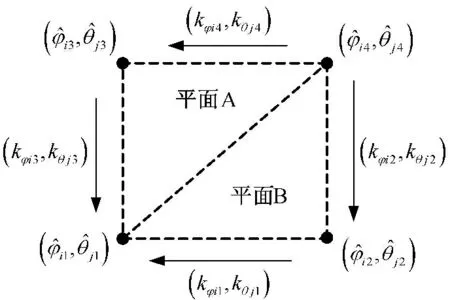
图4 指向误差平面划分及斜率对应关系图

四条边方位指向角的斜率计算公式为

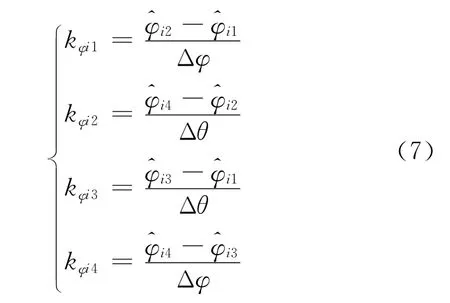
式中：Δφ 为四个波位方位方向理论上的波束指向间隔即Δφ ＝φi+1-φi。

四条边俯仰向指向角的斜率计算公式为

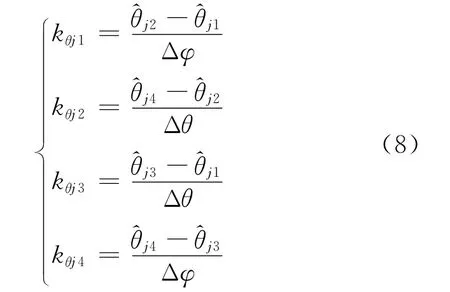
式中：Δθ为四个波位俯仰方向理论上的波束指向间隔即Δθ＝θj+i-θj。

对于区域内预期波束指向（φ，θ），可求得到波束控制器执行的指向角（φc，θc）。当（φ-φi）≥（θ-θj）时，控制器执行的指向角为

当（φ-φi）＜（θ-θj）时，控制器执行的指向角为

利用线性插值法可以大大缩小所需波束指向的测试量，例如按照2°×2°范围对波束指向区域划分时，所需测试波位数量由原来的14.4 M 减小为37.2k。波束指向区域划分得越小，线性插值得近似度越高，所获得的波束指向补偿效果也越好，所需要测量的波位数量也越多。工程中，应当根据实际需要的波束指向精度确定波束指向区域划分的大小。

4 测试验证

以某相控阵天线为例，采用6位移相器，单元间距为d ＝λ／2，阵面单元数量约为500，单元之间按照矩形排列。方位角、俯仰角波束指向由图2定义。按照2°×2°间隔测试离轴角60°以内的波束指向误差情况。实测二维波束指向误差如图5所示，图5（a）为补偿前方位指向误差，图5（b）为补偿前俯仰指向误差。从测试结果中可知，随着波束指向偏离阵面法线方向的角度增加，波束指向误差也逐步增加。在-60°～+60°的扫描范围内方位指向误差和俯仰波束指向误差可达0.8°。

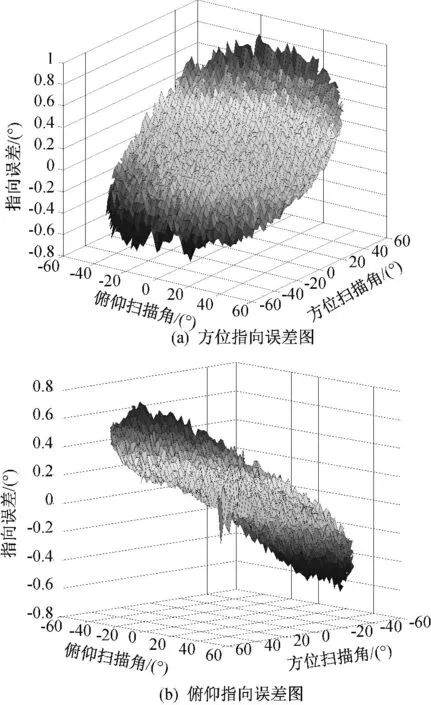
图5 补偿前二维波束指向误差测试结果

按照2°×2°进行区域划分后，采用线性差值法进行波束指向误差补偿，补偿后测试结果如图6所示，图6（a）为补偿后方位指向误差，图6（b）为补偿后俯仰指向误差。

由图可见，补偿后的波束指向的最大误差不不超过0.1°。

图6 补偿后二维波束指向误差测试结果

5 结束语

本文提出并详细介绍了相控阵天线波束指向误差的线性插值补偿法。该方法能有效减小相控阵天线波束指向的测试工作量，并降低波束控制系统的数据存储量，有利于工程实现。通过比较某相控阵天线补偿前后波束指向误差，验证了线性插值补偿法的有效性。

［1］ 贲德.韦传安.林幼权.机载雷达技术［M］.北京：电子工业出版社，2006：191.

［2］ 黄槐.齐润东.文树梁.制导雷达技术［M］.北京：电子工业出版社，2006：277

［3］ 沈文辉.周希朗.宫新保.提高相控阵天线波束指向精度的方法［J］.上海交通大学学报，2004，38（2）.

［4］ SHEN Wen-hui，GUO Yan-chang，Jiang Wei，etc.Beamsteering Optimized by Appropriate Random Phasing Quantization Methods［A］.ISAPE 2000.5th International Symposium on［C］.Beijing：House of Electronics Industry，2000：439-422.

［5］ 张光义.相控阵雷达原理［M］.北京：国防工业出版社，2009：52.

［6］ 盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2003：153.

［7］ 杨晋云.相控阵天线波束指向精度研究［D］.西安：西北工业大学，2004.