分解剖析 溯源归一

黄志琴

分解剖析 溯源归一

黄志琴

分类是初中数学第一个运用频繁并“隆重”介绍的数学思想方法.分类讨论题让同学们“爱恨交错”——具有挑战性而很难攻克.其实分类是有章可循，标准是它的基础，顺序是分类全面的保障.

问题一 怎样把 ||a的绝对值去掉？在数学问题中当我们不能确定时就需要分类.分类是需要标准的，想一想，它的分类标准是什么？正数、负数和零.与数的组成相关的分类讨论：比较数的大小，有理数的加法、乘法法则，化简二次根式等等.我们需要逐个依次考虑：负数、0、正数.

例1 化简代数式 ||x+1+ ||x-2及求它的最小值.

例2 已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表：

（1）求该二次函数的关系式；

（2）当x为何值时，y有最小值，最小值是多少？

（3）若A（m，y1），B（m+1，y2）两点都在该函数的图像上，试比较y1与y2的大小.

【点拨】例1中我们需要找到两个“0”点，并且组合分成“三段”（结合数轴更清晰）.

例2中的第（3）问，思路一，可转化为y1-y2的差与0的比较（“0”点），根据m的取值范围比较y1、y2的大小，这是函数应用中的常见问题.思路二，函数图像关于直线x=2对称，先确定相等时m的值为（“0”点值），在此基础上分类.亲爱的同学，解这一类题的关键是什么？

问题二 有一条道路和两个养鸡场.把这条道路看成一条直线l，两个养鸡场分别看成点A与点B，点A、B与直线l有多少种不同的位置关系？画出各种可能位置的图形.不同的位置，需逐个考虑.

例3（点在线上）已知一条直线上有A、B、C三点，线段AB的中点为P，AB=10，线段BC的中点为Q，BC=6，则线段PQ的长为___.

例4（点在线外）如图1，已知∠AOB.

（1）用直尺和圆规作射线OP，使OP⊥OB，

并分别作∠POA、∠AOB的平分线OM、ON；（2）求∠MON的度数.

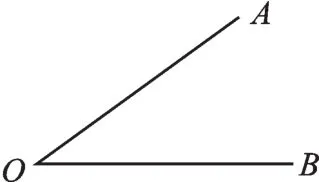
图1

【点拨】例3中直线被点A、B分成三部分，点C相对于点B的位置可以在左侧或右侧，需要分类.

例4因为点P位置可以在直线OB的两侧，射线有2条，图形有2种.

问题三 当图形特殊化，放在平面直角坐标系或圆的背景中时，题目就变得复杂，需要分解剖析.

（1）求点A、B的坐标；

（2）点P是x轴上一点，问平面上是否存在点Q，使得以A、B、P、Q为顶点的四边形为菱形，若存在，写出Q的坐标；若不存在请说明理由.

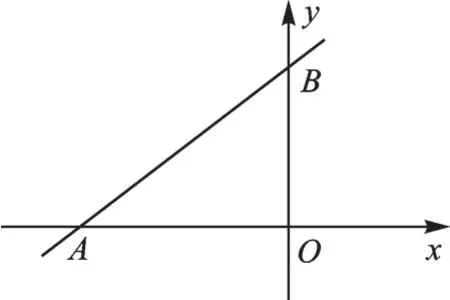
图2

【点拨】已知两个点确定一条线段，线段AB可以是未知菱形的边或对角线，需要分类.点P的位置是在x轴上，即第二条边的所在直线确定，存在4个菱形，点Q的位置如下：Q1（5，3）、Q2（-9，3）、Q3（0，-3）、Q4（-，3）.

特殊图形形状特殊，其中存在构成元素的特殊关系，定义和性质是我们考虑的分类标准.又如等腰三角形的边、角之间的特殊关系是我们分类的标准.确定能确定的，缩小范围，有条理地简化复杂问题.

小试身手

1.如图3，A（-5，0），B（-3，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB.∠CDA=90°.点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时间为t秒.

（1）求点C的坐标；

（2）当∠BCP=15°时，求t的值；

（3）以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值.

图3

2.直线y=x+3与x轴、y轴分别交于点A、C，经过A、C两点的抛物线y=ax2+bx+c与x轴的另一交点为B，顶点P的横坐标为-2.

（1）求该抛物线的表达式；

（2）连接BC，得△ABC.若点D在x轴上，且以点P、B、D为顶点的三角形与△ABC相似，求出点D的坐标.

图4

（作者单位：江苏省常州市金坛区白塔中学）

扫二维码关注“初中生世界”公众号，回复“2017年6月数学”获取答案。