整体思想在解题中的巧用

吴粉连

整体思想在解题中的巧用

吴粉连

有一些数学问题，如果从局部入手，难以各个突破，但若能从宏观上进行整体分析，运用整体思想方法，则常常能出奇制胜，简捷解题.

整体思想，就是在研究和解决有关数学问题时，通过研究问题的整体形式、整体结构、整体特征，从而对问题进行整体处理的解题方法.整体思想的主要表现形式有：整体代换、整体设元、整体变形、整体补形、整体配凑、整体构造等等.在初中数学中的数与式、方程与不等式、函数与图像、几何与图形等方面，整体思想都有很好的应用，因此，每年的中考中涌现了许多别具创意、独特新颖的涉及整体思想的问题，尤其在考查高层次思维能力和创新意识方面具有独特的作用.下面就初中数学中整体思想的应用及解题策略谈一些看法和体会.

一、整体代换

整体代换是根据问题的条件和结论，选择一个或几个代数式，将它们看成一个整体，灵活地进行等量代换，从而达到减少计算量的目的.

例1 已知a+d2=2007，b+d2=2008，c+d2= 2009，且abc=24，求的值.

【解析】由已知解出a、b、c的值再代入求解，计算将很复杂，因此选择如下的整体代换：

由已知可得：a-b=-1，b-c=-1，c-a=2，则原式

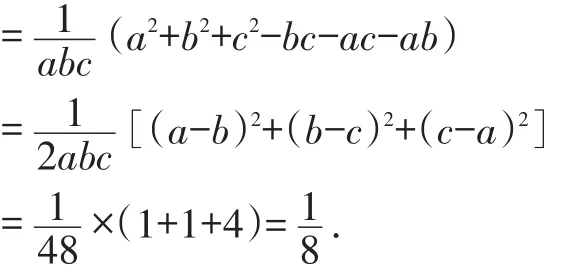
二、整体设元

整体设元是用新的参元去代替已知式或已知式中的某一部分，从而达到化繁为简、化难为易的目的.例2 计算

【解析】本题数据较多，直接计算显然无法进行，注意到题中出现的相同算式，因而考虑整体设元.

三、整体变形

整体变形是将问题中某些局部运算作整体变形处理，使之呈现规律性的结构形式，从而达到简化问题或减少运算量的目的.

【解析】观察式子特点，用凑整法可简化运算.

四、整体补形

整体补形是根据题设条件将原题中的图形补足为某种特殊的图形，创造题设条件与特殊图形之间的关系，从而突出问题本质，找到较简洁的解法或证法.

例4 如图1，在四边形ABCD中，AB=2，CD=1，∠A=60°，∠B=∠D=90°，求四边形ABCD的面积.

图1

【解析】这是一个不规则的四边形，欲求它的面积，可把它补成三角形或规则的四边形，所求图形的面积恰是两个图形面积的差.

延长AD、BC相交于点E，如图1，

在Rt△ABE中，∠A=60°，AB=2，

∴BE=AB·tanA=23，

Rt△CDE中，CD=1，

∠ECD=180°-∠BCD=60°，

∴DE=CD·tan∠ECD=1×tan60°= 3.

S四边形ABCD=S△ABE-S△CDE==

【说明】本题还可以把原四边形补成一个矩形、直角梯形、等边三角形或平行四边形，如图2、图3、图4、图5.

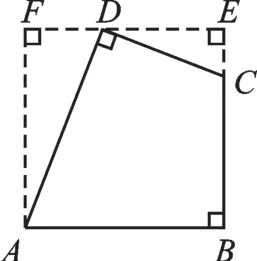
图2

图3

图4

图5

五、整体配凑

整体配凑是将问题中的条件和结论进行适当的配凑，使之结构形式特殊化、公式化，再利用相关性质进行求解，以达到解答问题的目的.

例5 若a+2b+3c=12，且a2+b2+c2=ab+bc+ ca，则a+b2+c2= .

【解析】要求a+b2+c2的值，需求a、b、c的值，但已知等式只有两个，若按常规方法是无法解决的.注意到a2+b2+c2=ab+bc+ca，可采取整体配凑的方法，借助于非负数的性质，找出a、b、c之间的关系，再利用a+2b+3c=12就可以求出a、b、c的值.事实上，由a2+b2+c2=ab+bc+ca，有2a2+2b2+2c2-2ab-2bc-2ca=0，即（a-b）2+（b-c）2+（c-a）2=0，故a=b=c，将之代入a+2b+3c=12，得a=b=c=2，故a+b2+c2=10.

六、整体构造

整体构造是把问题中某些代数式赋予具体的几何意义，构造出几何图形，利用数形结合的思想来解答问题.

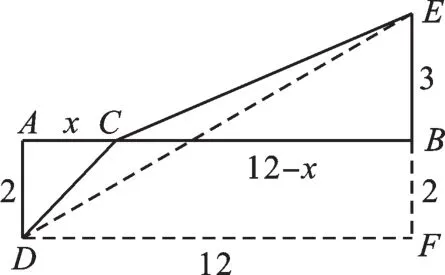
图6

（作者单位：江苏省常州市金坛区华罗庚实验学校）