等级访问控制下密文数据库密钥管理方案研究*

胡前伟，李子臣，闫玺玺

1.北京印刷学院 信息工程学院，北京 102600

2.河南理工大学 计算机科学与技术学院，河南 焦作 454003

等级访问控制下密文数据库密钥管理方案研究*

胡前伟1,2+，李子臣1，闫玺玺2

1.北京印刷学院 信息工程学院，北京 102600

2.河南理工大学 计算机科学与技术学院，河南 焦作 454003

HU Qianwei,LI Zichen,YAN Xixi.Research on key management scheme for hierarchical access control in database.Journal of Frontiers of Computer Science and Technology,2017,11(6)：921-931.

针对等级体制下用户权限管理和访问密文数据库的问题，提出了基于椭圆曲线密码体制的密钥管理方案。该方案中每个用户都可以独立选择自己的用户密钥，并安全传送给可信中心，可信中心在收集完密钥参数之后使用椭圆曲线密码体制计算出具有偏序关系的用户关系参数。高级别用户利用关系参数和用户密钥便可以安全有效地推导出低级别用户的密钥信息，然后利用密钥信息解密低级别用户的密文数据库。方案中还考虑了偏序关系变化后密文数据库的更新方法。实验表明，安全等级的密钥推导和访问数据库具有较高的效率和安全性。

密文数据库；密钥管理；椭圆曲线密码体制；偏序关系；用户分级

1 引言

近年来数据库安全技术迅速发展，数据库加密技术就是其中众人认可的一项安全技术。加密之后的数据足以抵挡入侵者的大部分攻击和破坏，安全可行的密钥管理方案可以提高整个系统的效率和安全性。合理可靠、安全稳定的数据库加密技术是众多学者的研究方向，并且具有一定的深度和广度，不仅要考虑数据库加密层次、加密算法的选择、加密粒度的选择和密钥管理方案的构思等问题，还要考虑同态技术、数字水印、格、量子力学等技术是否能与之结合来满足人们对数据库不同方面的需求。等级体制下数据库加密技术就是其中一种，而等级体制是将用户按照安全等级分成不同的等级组，高级别用户可推导出低级别用户的密钥信息，反之则不成立。在等级这个环境下构造和实施数据库加密技术，可以应用在企业部门、军事部门和政府机关等各类组织机构中提升数据的安全性和可靠性。

在等级访问控制下，要对每个用户分配等级属性密钥，也就需要管理这些密钥，而密文数据库中同样需要管理密钥，那么在等级访问控制条件下实施数据库加密技术就要考虑如下几个问题：

（1）如何构造等级用户之间安全高效的密钥管理方案；

（2）如何实施数据库加密技术，如何解决各类密钥在生命周期内的生成、分配、更换和注销等问题；

（3）等级用户访问密文数据库，如何解决等级访问控制下数据库密钥管理方案的安全性、高效性、完整性等问题。

考虑到上述问题，本文结合等级系统和密文数据库，提出了基于椭圆曲线的密文数据库密钥管理方案。本文方案使用椭圆曲线密码体制构造辅助参数，高级别用户可以安全有效地推导出低级别用户的密钥信息，然后利用密钥信息解密低级别用户的密文数据库，得到明文数据。等级密钥管理方案与密文数据库密钥管理方案有机结合，可有效解决等级体制下用户权限管理和访问密文数据库的问题。

2 相关研究工作

（1）等级访问控制下的密钥管理

早在1983年，Akl等人[1]考虑到等级系统下密钥管理问题，高级别用户可以推导出低级别用户的密钥信息，反之不可行，而这种思想一直贯穿于后来众多研究当中。Lin在文献[2]中提出了基于动态密钥管理的访问控制方案，该方案中的密钥推导基于求解离散对数问题。后来的等级密钥管理方案有基于中国剩余定理（Chinese remainder theorem，CRT）[3]、基于单向散列函数（one-way Hash function）[4]等。如Zych等人[5]提出的强制访问控制下密钥管理方案，每个用户存储一个Key值，可以有效计算出所请求访问数据的密钥，方案中密钥推导基于Diffie-Hellman。又如Zhang等人[6]提出了等级密钥管理方案中基于大素数因式分解困难性问题，在管理秘密密钥时使用了中国剩余定理和单向散列函数，减少了公共参数的存储空间。近年来的研究中，针对线性等级访问控制（linear hierarchical access control），Odelu等人[7]提出的动态密钥管理方案中，主要使用对称加密算法AES（advanced encryption standard）来解决动态等级访问控制问题，方案中减少了安全等级的密钥存储开销。而Basu等人[8]提出的等级访问控制下的动态密钥管理方案是改进了Wu等人[9]的密钥管理方案，使用椭圆曲线（elliptic curve cryptosystem，ECC）、AES和HASH的混合加密方案，减少了Wu方案中多余的计算。在Hwang-Yang[10]方案的基础上张建民等人[11]提出了一个新的基于等级系统的访问控制方案，该方案不仅利用中国剩余定理解决了Hwang-Yang方案中的安全问题，而且所需的存储空间更少，密钥的生成和导出效率更高。在文献[12]中，孙佳思提出了一种新的基于ECC算法的等级密钥管理方案，该方案解决了在多项式时间内敌手利用求根算法进行攻击的安全漏洞问题。

（2）密文数据库下的密钥管理

密文数据库及密钥管理在这些年一直是被研究的热点，如Mahajan[13]和Shmueli等人[14]提出的数据库安全加密技术中都使用数据库Cache技术。前者的方案注重数据加解密效率，却忽略了系统安全性的提高。后者兼顾了性能和安全性，在数据库管理系统（database management software，DBMS）中的数据库Cache里设置一个加密模块，其选择的加密粒度是数据项，在加密数据时连同数据项的坐标也要加密。而Zhou等人[15]提出的数据库加密技术方案同样兼顾安全性和效率，在加密数据的同时生成B+树索引，并使用Kerberos协议保护索引的安全，考虑了系统的完整性。在Sarfraz等人[16]提出的针对密文数据库细粒度的访问控制方案中使用了属性集访问控制（attribute based access control，ABAC）模型，在密钥管理上使用了AB-GKM（broadcast group key management）方案和OCBE（oblivious commitment based envelope）协议，提高了访问数据的灵活性。针对密文数据库中密钥管理问题，Sun等人[17]提出的基于中国剩余定理的密钥管理方案中使用身份认证机制提高了用户、DBA（database administrator）和数据Creators之间的安全度和信任度。文献[18]中戴一奇等人提出了密钥转换表方案，使用两级转换表的方式实现对数据的解密，但是该方案可靠性不理想。文献[19]中肖飞等人提出了基于密文角色的密钥管理方案，使用角色方便对用户权限的管理，但是该方法忽略了一个角色对应多个数据项问题，解密时需要多次操作，不可避免地影响了效率。

无论是等级访问控制下的密钥管理，还是密文数据库下的密钥管理，都要考虑方案的统一性、全面性，要兼顾系统的性能和安全。

3 密钥管理方案

3.1 形式化定义

密钥管理方案中，可以使用一些基本模型来描述密文数据库及用户。数据库就是一个集合D= {d1,d2,…,dn}，di表示安全性要求相同且可用同一数据密钥加密的一类数据，它可以是表、记录、字段、数据项的一种。对应的密钥集KD={kd1,kd2,…,kdn}，它有加解密算法(E,D)，密文数据库C={c1,c2,…,cn}，其中ci=E(kdi,di),i∈[1,n]。

在密文数据库中，各个用户实体之间都有安全等级，假设用户实体集合为U={u1,u2,…,un}，那么用户ui和uj之间存在等级关系，这种关系可以用偏序进行描述。

定义1设L⊆U×U且U≠∅，如果L具有自反性、反对称性和传递性，则称L是U上的偏序关系，将这种偏序关系记为≤，若x与y存在偏序关系，则记为x≤y。

定义2在一个有序二元组中，V是图的顶点集，E是图的边集，有E⊆V×V且对于任意的α,β,η,eη=∈E，vα≠vβ，则称它为有向无环图，记为DAG（directed acyclic graph）。

定义3在有向无环图中，对于任意的i,j,k,ek=∈E，且vi≤vj，则称vj是vi的前驱节点，vi是vj的后驱节点。

根据有向无环图的特点，假设节点代表用户实体，有向边代表用户实体之间的偏序关系，那么有向边连接的是父节点和子节点，比如ui≤uj，uj是父节点，而ui是子节点，也就意味着uj的等级权限高于ui的等级权限，那么uj可以访问到更多的资源。在密文数据库中，每个等级用户都会使用自己的密钥加密数据库中的数据，等级高的用户也就有权限解密或者查看等级低的用户的数据。如果用户ui的密钥为ski，而用户uj的密钥为skj，且ui≤uj，那么密钥skj可以推导出ski，反之一定不成立。

3.2 密钥构造

在密文数据库的密钥管理方案中，首先每个用户uj可以自主选择用户密钥ukj。将ukj安全地传送给可信中心TC（trusted center），在收集完密钥参数之后计算出具有偏序关系的用户的关系参数，具体步骤如下。

步骤1可信中心TC在GF(p)中选择椭圆曲线Ep(a,b)和基点G，p是大素数，n为点G的阶，并公布Ep(a,b)、G和n。

步骤2uj选取[1,n-1]之间的随机参数rj，并计算Ψj=rj∗G，H(ukj||rj)=Θj，H表示hash函数，最后公布参数Ψj和Θj。

步骤3TC为该用户选取随机整数dj，dj∈[1,n-1]，计算Ζj=dj∗G，skj=H(Zj||Θj)，skj是用户访问数据库时需要的密钥，也是等级用户之间推导的密钥，下面使用SK表示，将skj秘密传送给数据库服务器。

步骤4对于所有的等级用户ui只要满足ui≤uj，1≤i≤n，TC就计算Cji=di∗Ψj，将Cji作为关系参数，如图1所示。TC创建三元组，并保存。

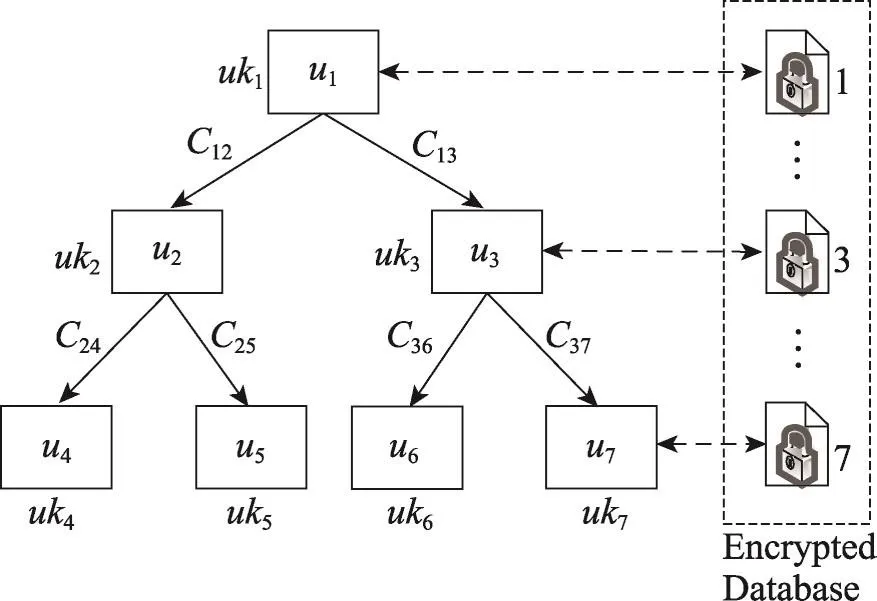
Fig.1 Key management scheme图1 密钥管理方案

3.3 密钥推导

等级高的用户uj才可以有权限推导出低等级用户ui的用户密钥信息，例如ui≤uj，密钥构造过程中会产生关系参数Cji，用户uj利用该参数计算出ui的密钥信息ski，步骤如下所示。

步骤1uj希望获得与ui的关系参数，向可信中心TC发送查询请求，TC通过三元组判断uj与ui是否存在偏序关系，若存在，则返回关系参数Cji给用户uj。

步骤2uj得到Cji，然后计算di∗G=Zi，就可以得到ski=H(Zi||Θi)，用户uj得到ui的密钥ski便可以访问用户ui的密文数据库。

在用户实体和等级权限构成的有向无环图中，TC为所有的具有偏序关系的两个等级用户构造关系参数，高级别用户便可以推导出低级别用户的密钥信息。

3.4 访问密文数据库

当高级别用户获取到低级别用户的密钥信息后，就可以访问密文数据库。目前针对密文数据库的密钥管理方案中以多级密钥管理为主，本文访问密文数据库的过程中涉及到两种密钥：系统主密钥和工作密钥。其中，工作密钥就是对数据库中的数据进行加解密的密钥，它可以是表密钥、字段密钥、行密钥和数据项密钥，本方案中是对数据项进行加密，那么工作密钥也就是数据项密钥；而系统主密钥就是用来保护工作密钥的。在密钥构造和密钥推导过程中，使用到的仅仅是用户密钥，有了用户密钥，就可以解密出系统主密钥，接着解密出数据项密钥，用数据项密钥解密密文，便可以看到明文数据。如图2所示。

图2中，u1与u2表示等级用户，它们的用户密钥分别是uk1和uk2，Kmaster_1、Kmaster_2表示系统主密钥，Kwork_1、Kwork_2表示工作密钥，D1、D2表示密文数据。TD是可信中心，C12是u1、u2的关系参数。过程（Ⅰ）表示用户u1访问自己的密文数据库的过程，过程（Ⅱ）表示u1访问u2的密文数据库的过程。这两个过程的具体步骤如下。

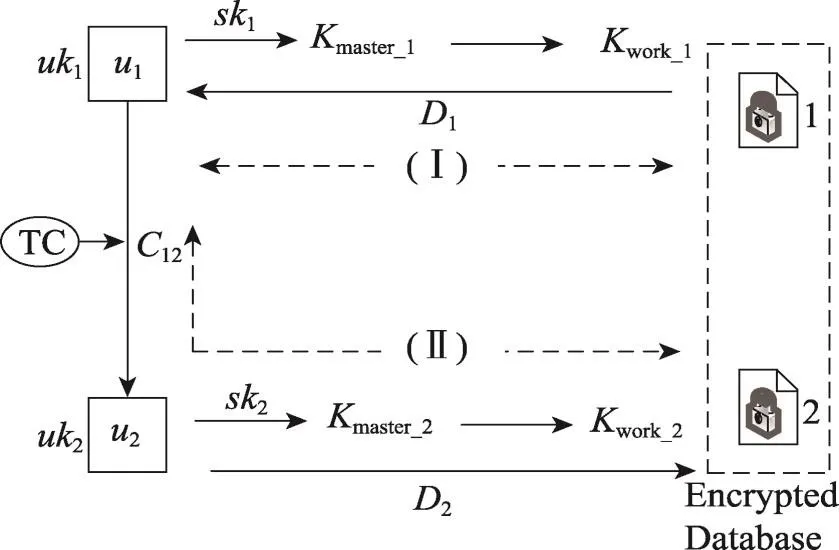
Fig.2 Accessing encrypted database图2 访问密文数据库

步骤1每个等级用户都有自己的密文数据库，都可以加解密数据。如图2，在密钥构造阶段会产生密钥sk1发送DBMS，在加密完数据库后，使用密钥sk1加密系统主密钥，并且加密后的系统主密钥由单独的硬件安全模块（hardware security module，HSM）存储[20]保护。

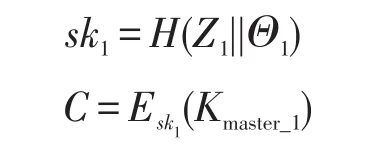
其中，Z1=d1∗G，Θ1=H(uk1||r1)，d1和r1分别是用户和TC选择的，且d1，r1∈[1,n-1]。

那么当用户访问密文数据库时，需要解密出系统主密钥。

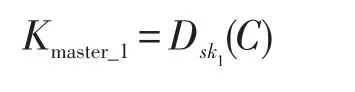
步骤2系统主密钥保护数据项密钥，有了系统主密钥就可以解密出数据项密钥。本方案中数据项密钥是以表的形式存放到数据库中的，表结构比较简单，如表1所示。

Table 1 Data item key table表1 数据项密钥表

在数据库当中由系统主密钥加密上述的数据项密钥表，考虑到加解密的效率，精简了数据项密钥表，提高了密文数据库的效率。其中，d_ID是数据项标志；d_K是数据项密钥，是在数据加密时生成的；ξ表示加密数据项的个数。数据库中每张数据表都有表密钥T_K，并且数据库中每个记录都有行参数Ri(i∈[1,n])，每个属性都有列参数Fj(j∈[1,m])。当用户选择要加密的数据项dij时，可以判定数据所在的行及列，找出行参数Ri和列参数Fj，然后可计算d_ID_τ=f1(Ri,Fj)，d_K_τ=f2(T_K,Ri,Fj)，τ∈[1,ξ]，f1和f2分别为生成数据项标志函数、生成数据项密钥函数。将d_ID_τ和d_K_τ存入数据项密钥表中，当用户加密完数据后，由系统主密钥Kmaster加密整张数据项密钥表。解密时，需要用系统主密钥解密数据项表，然后选择要解密的数据项。因为数据库的数据项是有序加密的，所以同样可以获取到行参数Ri和列参数Fj，计算d_ID_τ=f1(Ri,Fj)，在数据项密钥表中查询出对应的数据项密钥，解密该数据项。

当上级用户要访问下级用户的密文数据库时，也即要完成图2中过程（Ⅱ），首先需要推导出下级用户的SK密钥，然后按照上述的步骤访问数据库即可。

3.5 动态管理

在实际当中，用户实体是处于变动的，会出现用户修改密钥，增加等级关系，删除等级关系和增加新的等级用户的问题，这些用户实体及等级的变化都会对密文数据库产生相应的影响。下面将具体研究这4种情况下密文数据库的密钥管理问题。

（1）修改用户密钥

当用户uj将用户密钥ukj修改为ukj′时，需要将新密钥重新发送给可信中心TC，若ui是其后驱节点，则计算过程为：

步骤1uj重新选择随机参数rj′∈[1,n-1]，计算重新发布

步骤2TD重新选取随机整数dj′，dj′∈[1,n-1]，计算将作为关系参数，并将重新发送给数据库服务器。

由于系统主密钥被SK密钥skj加密保护，用户密钥更改后，则需要先用SK密钥解密系统主密钥，再将新用户密钥加密系统主密钥

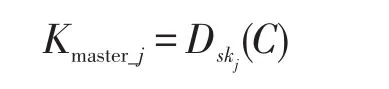
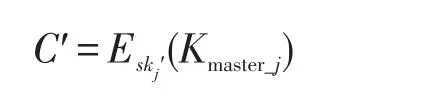
（2）增加等级关系

如图1所示，如果用户u1与用户u5之间存在偏序关系，也即u5成为u1的后驱节点，那么可信中心TC只需要计算C15=d5∗Ψ1，d5是TC为用户u5选取的随机整数，Ψ1是用户u1公布的参数。此时，用户u1和用户u5的密文数据库不做任何变化。如果用户实体之间的等级关系被删除，则可信中心TC直接删除它们之间的关系参数即可，密文数据库也不做任何变化。

（3）增加新的等级用户

当要增加新的等级用户时，则需要判断增加的等级用户的前驱节点和后驱节点，也即判断新增用户与哪些用户有从属关系，有了从属关系，便要计算两者之间的关系参数，密文数据库不做任何变化。

（4）删除等级用户

如图3所示，用户u3被删除后，与其关联的所有等级关系都被删除，且用户u3的密文数据库也要做相应的操作，具体处理步骤为：

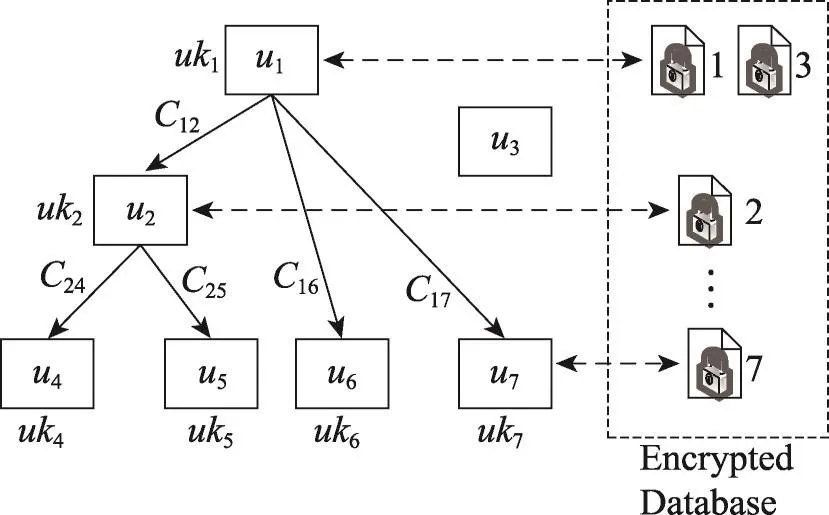
Fig.3 Deleting hierarchy user图3 删除等级用户

步骤1用u3的SK密钥sk3解密其密文数据库中的系统主密钥，再用其上级用户u1的SK密钥sk3加密该系统主密钥，此时，u3的密文数据库完全由u1管理。

步骤2判断被删除等级用户是否有后驱节点，若没有，则结束，若有，如图3所示的情况，则将这些等级用户与上级用户建立等级关系，在u1和u6及u1和u7之间分别建立等级关系，并由TC构造关系参数C16、C17。

4 方案分析

本文提出的密钥管理方案兼顾了等级访问控制和密文数据库特征，解决了密文数据库中等级用户之间的权限管理和动态访问密文数据库的问题。下面将从安全和性能两方面来分析本文的方案。

4.1 安全性分析

（1）反向攻击

椭圆曲线密码体制的安全性，依赖于椭圆曲线离散问题的难解性。反向攻击也就是低级别用户ui想推导出高级别用户uj的密钥信息skj，那么也就需要解决椭圆曲线离散对数问题（elliptic curve discrete logarithm problem，ECDLP），证明过程如下：

Ep(a,b)，G，n⇒可以计算出2p,3p,…,np，且有np=ο。椭圆曲线离散对数问题描述了给定一个椭圆曲线E，考虑本原元P和另一个元素T。则DL问题是找到整数d(1≤d≤n)，满足:

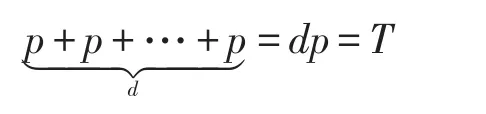
假设可以求出skj。其中skj=H(Zj||Θj)，Θj是公开参数，相当于可以求解出Zj，而Zj=dj∗G，G是公开参数，那么相当于可以求解出dj，这与椭圆曲线离散对数问题相矛盾，故ui推导不出skj。

（2）内部收集攻击

假设存在一个低级别用户ui有m个父节点uj,uj+1,…,uj+m-1，并收集了关系参数Cji,C(j+1)i,…,C(j+m-1)i，攻击者试图推导出其中一个父节点的用户密钥skε,ε∈[j,j+m-1]，内部收集攻击可以转换为求解下列方程组的过程。求证过程如下：

①在（1）中可知Zj=di∗Gdi

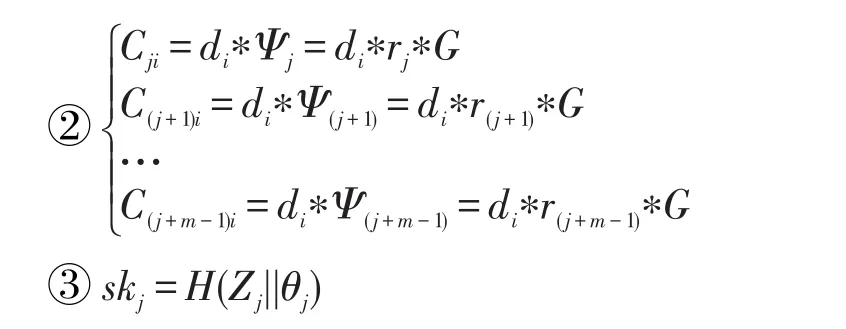
由①可知，在方程组②中，∀ε,ε∈[j,j+m-1],Cεi=di∗Ψε=di∗rε∗Grε。

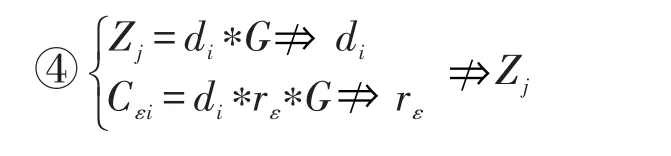
由③和④可知用户推导不出任何一个上级的密钥信息，因此这种攻击没有效果。

（3）外部收集攻击

类似第二种攻击，在图4中如果外部敌手收集到几个关系参数C25、C36、C37。因为不知道上级用户u2、u3的用户密钥及秘密参数，所以不可能计算出下级用户u5、u6、u7的密钥信息。分析如下：

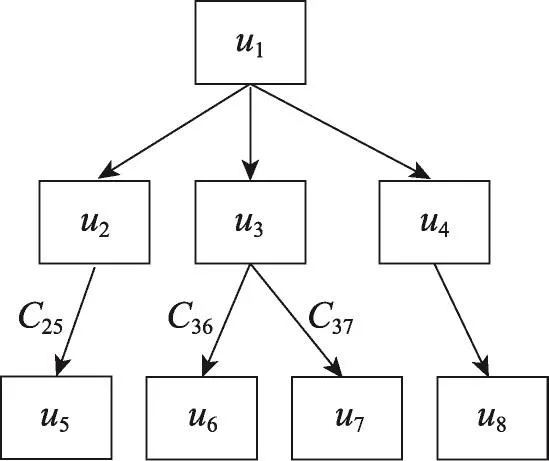
Fig.4 Exterior collecting attacks图4 外部收集攻击

分析关系参数C25可知C25=d5∗Ψ2，sk5=H(Z5||Θ5)，攻击者需要求解它们。

①在密钥构造过程中TC秘密计算出Z5

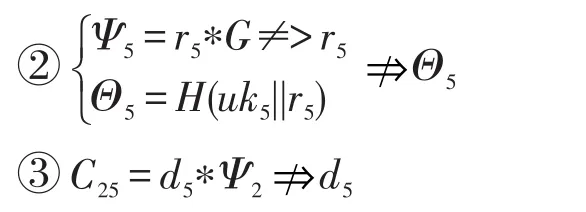
由①、②、③可知用户计算不出sk5，那么同理可知攻击者也不可能计算出u6和u7的密钥信息。

（4）同谋攻击和兄弟攻击

如图4所示，u3有两个低级别用户u6、u7，现在这两个用户一起攻击u3，攻击过程会遇到椭圆曲线离散对数问题。求证过程如下：

①在（1）中可知Zj=di∗Gdi

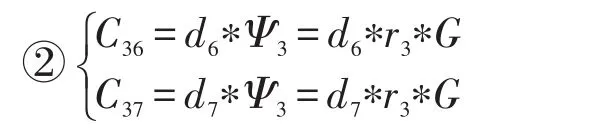
由①和②可知：

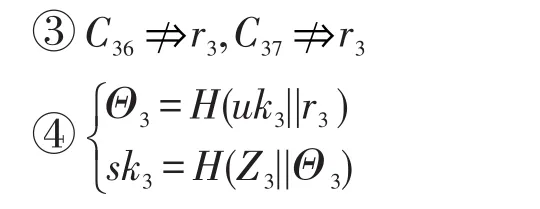
首先攻击者不知道uk3，其次由③和④可知攻击者计算不出sk3。如果图4中u6攻击同级别的u7，获取其密钥信息，便构成兄弟攻击。他不仅需要反向攻击上级用户u3，还要窃取关系参数C37，而反向攻击很难实施，因此兄弟攻击无效。

（5）唯密文攻击和密文统计攻击

攻击者试图从数据库中相同的密文以及明文统计信息来破解其中的明文。本方案中对不同数据使用不同的密钥，那么加密后结果就不会相同，即使相同的数据在用不同密钥加密后，密文数据仍不一样，密文统计攻击在密文数据库中是不会成功的。分析过程如下：

在密文数据库加密过程中，使用密钥生成函数来生成工作密钥，d_k=ET_K(Ri)⊕ET_K(Fj)，E是分块加密算法。在n行m列的数据库表中，行和列的参数有如下规则：

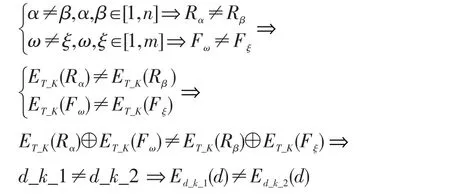
4.2 性能分析

可信中心TD生成关系参数，等级用户进行密钥推导都需要一定的计算开销和存储开销。下面主要针对等级系统中的时间开销及存储开销和密文数据加解密效率进行测试，并与其他几个方案进行对比分析，得到如下结果。

Basu方案[8]、Morteza方案[21]和孙方案[17]提出的等级系统中的密钥管理方案都使用了椭圆曲线密码，但是这些方案中用户都不能自主选取用户密钥，需要可信第三方生成，并且Basu方案中将AES加密方法用于等级用户之间密钥的推导，略比Morteza方案复杂。而本方案中用户可以自主选取用户密钥，也是实现动态密钥管理。表2列举了性能分析所需要的符号定义，并且每种操作所需要的时间可以转换为相应TMUL时间[8,21]，如表3所示。

本文方案基于椭圆曲线密码体制，在密钥构造阶段有3次ECC乘法和2次哈希运算，故需要的时间为在密钥推导过程中有1次求模运算、1次ECC乘法运算和1次哈希运算，所需时间为Morteza方案[21]的密钥构造过程中有3次ECC乘法和1次哈希运算，所需时间为(2TECC_MUL+THASH)+(vi+1)TECC_MUL=[2 400.36+1 200(vi+1)]TMUL，而密钥推导过程所需时间同本方案一样。同样可计算出Basu方案[8]和孙方案[17]的密钥构造和密钥推导过程的时间花销。

Table 2 Symbol definition of performance comparison表2 性能比较的符号定义

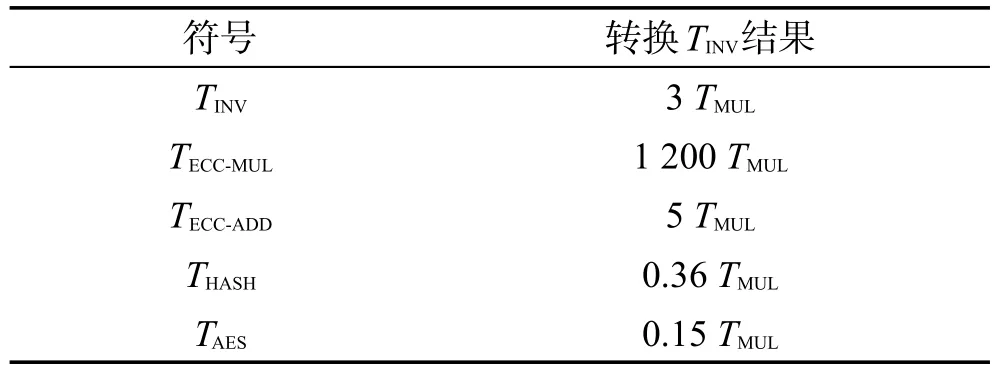
Table 3 Operation time conversion表3 操作时间转换

在这两个过程中都需要存储相关的数据，会占用一定的空间。在椭圆曲线密码体制中，为保证密码的安全性，参数的选取大小一般大于或等于163 bit。Basu方案[8]中，可信中心TC需要存储的有私钥dTC及公共区域中的参数，而私钥大小是163 bit，公共区域中有公钥Qi和公共参数mij，存储空间为Morteza方案[21]对认证中心CA没有要保密的参数，公共区域内，仅仅需要存储个公共参数，因此需要2n×163的空间。而本文方案中不仅需要存储个参数，还需要存储128bit的哈希参数。孙方案[17]中在公共区域需要的存储空间为(3n+4)×163，而等级用户也仅需要163 bit的空间。

如表4、表5所示，本文方案的存储及时间开销都低于Basu方案[8]、孙方案[17]和Morteza方案[21]，并且这两个方案中用户没有自己选取用户密钥的权限，只能由可信第三方来生成。本文方案改进了这一缺陷，用户不仅需要随机选取用户密钥，还可以动态管理密钥。在测试密文数据库时，方案中使用了不同的加密算法来加密数据表中的数据项，并且不同数据项使用不同的密钥，以保证加密后的数据不会重复，避免统计攻击。在测试密文数据库中，以C#为开发环境，其中的数据项标志函数为d_ID=hash512(Ri||Fj)，数据项密钥生成函数为d_K=ET_K(Ri)⊕ET_K(Fj)，E是AES加密算法。

Table 4 Time cost comparison表4 时间开销比较

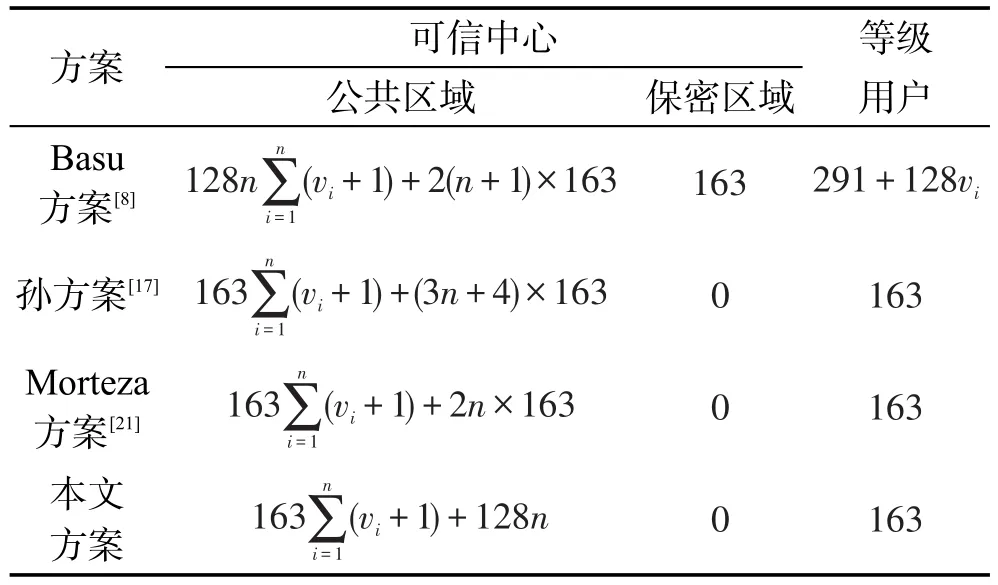
Table 5 Storage overhead comparison表5 存储开销比较

图5~图8是密文数据库中的数据项加密和解密的时间对比图，实验中选取了AES、3DES和IDEA加密算法。从图5、图6可知，在密文数据库中，对数据项加密时，选取不同的加密算法会直接影响数据加解密效率，针对不同大小的数据项进行加解密时，IEDA使用的时间都比较少，且加解密的时间差不大。当选取不同数量的数据项进行加解密时，出现的情况如图7、图8所示，每种加密算法的效果基本上相差不大，IDEA和3DES的加解密效率低于AES。从这些比较中可以得知，针对单个数据项的加解密可以选择IEDA算法，但是加解密多个数据项时这3种算法都可以使用。

4.3 实现比较

表6汇总了几种方案的实现，比较了使用技术、方案结构、访问类型、自定义密钥以及是否能与密文数据库结合。其中树结构是有向无环图的特定形式，但灵活性不够。直接访问是高级别用户可访问任何低级别用户密钥信息，而间接访问模式中高级别用户只能访问其直接后继。自定义密钥也就是用户是否具有自主选择用户密钥的能力，它直接影响到是否能应用到密文数据库中。在密文数据库密钥管理方案中，每个用户只能保存、更换或删除自己的密钥，有了自定义密钥的能力，也就可将等级访问控制应用到密文数据库中。

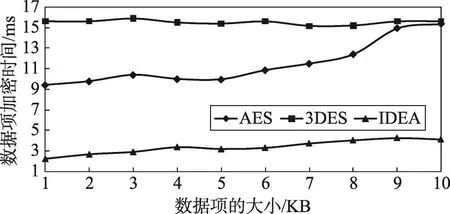
Fig.5 Encryption time comparison of different sizes of data items图5 不同大小的数据项加密时间比较

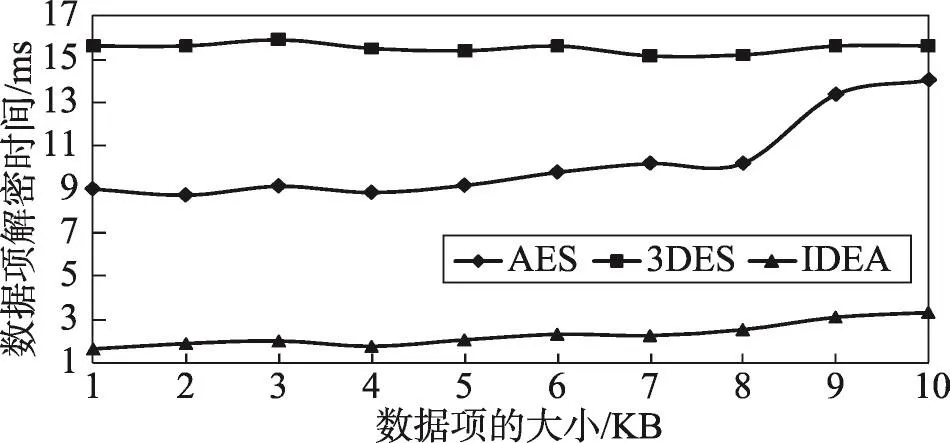
Fig.6 Decryption time comparison of different sizes of data items图6 不同大小的数据项解密时间比较

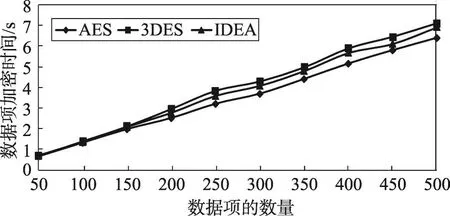
Fig.7 Encryption time comparison of different number of data items图7 不同数量的数据项加密时间比较

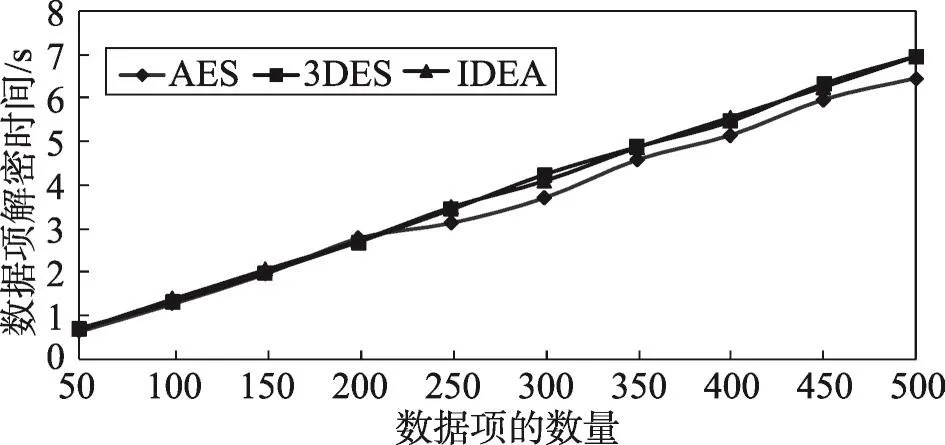
Fig.8 Decryption time comparison of different number of data items图8 不同数量的数据项解密时间比较

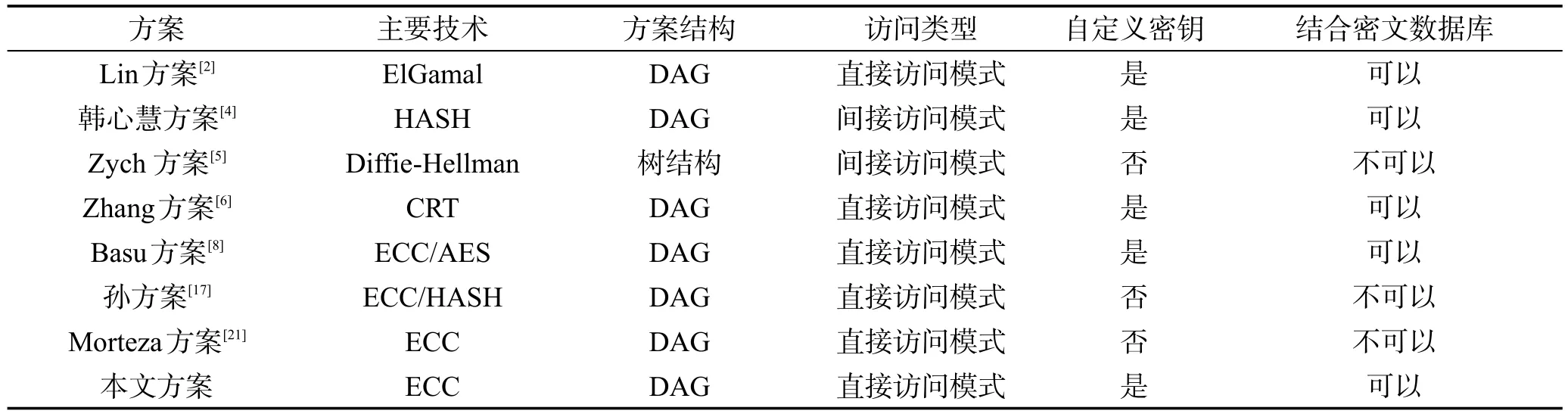
Table 6 Comparison of different schemes表6 方案实现比较

5 结束语

将密文数据库应用到等级环境中，可以满足等级用户之间访问密文数据库的需求，特别是在企业部门、军事部门和政府机关等各类组织机构中，一方面它具备等级特性，另一方面它可以对数据进行加密存储。本文方案考虑到这种特定需求，研究出基于椭圆曲线密码体制的密钥管理方案，等级用户在密钥构造和密钥推导后可以访问密文数据库中数据。方案分析显示，它可以抵抗相应的攻击，占用较小的空间和时间开销，密文数据库的测试中使用不同的加密算法对数据项进行加密。下一步将考虑在等级环境中对密文数据库的表、属性和记录进行加密测试，改进密钥构造、密钥推导以及密文数据库中的密钥管理方案，进一步提高密钥管理方案的效率和安全性，并应用到实际需求当中。

[1]Akl S G,Taylor P D.Cryptographic solution to a problem of access control in a hierarchy[J].ACM Transactions on Computer Systems,1983,1(3):239-248.

[2]Lin C H.Research:dynamic key management schemes for access control in a hierarchy[J].Computer Communications,1997,20(15):1381-1385.

[3]Xu Yanyan,Xu Zhengquan,Chen Xi.A hierarchical key management scheme using Chinese remainder theorem[J].Journal of Huazhong University of Science and Technology: Natural Science Edition,2010,38(12):65-68.

[4]Han Xinhui,Long Qin,Si Duanfeng,et al.A practical hierarchical key management scheme based on one-way Hash function[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2008,44(4):527-536.

[5]Zych A,Petković M,Jonker W.Efficient key management for cryptographically enforced access control[J].Computer Standards&Interfaces,2008,30(6):410-417.

[6]Zhang Jianmin,Li Jian,Liu Xiande.An efficient key management scheme for access control in a user hierarchy[C]// Proceedings of the 2009 International Conference on Information Technology and Computer Science,Kiev,Ukraine, Jul 25-26,2009.Piscataway,USA:IEEE,2009:550-553.

[7]Odelu V,Das A K,Goswami A.LHSC:an effective dynamic key management scheme for linear hierarchical access control[C]//Proceedings of the 5th International Conference on Communication Systems and Networks,Bangalore,India, Jan 7-10,2013.Piscataway,USA:IEEE,2013:1-9.

[8]Basu A,Sengupta I.Improved secure dynamic key management scheme with access control in user hierarchy[C]//Proceedings of the 2nd International Conference on Digital Information&Communication Technology&Its Applications, Bangkok,Thailand,May 16-18,2012.Piscataway,USA: IEEE,2012:220-225.

[9]Wu Shuhua,Chen Kefei.An efficient key-management scheme for hierarchical access control in E-medicine system[J].Journal of Medical Systems,2012,36(4):2325-2337.

[10]Hwang M S,Yang Weipang.Controlling access in large partially ordered hierarchies using cryptographic keys[J].The Journal of Systems and Software,2003,67(2):99-107.

[11]Zhang Jianmin,Liu Xiande,Xu Haifeng.New scheme for access control in hierarchy security systems[J].Computer Engineering andApplications,2007,43(16):156-158.

[12]Sun Jiasi.Research on key management method based on elliptic curve cryptosystem[D].Hohhot:Inner Mongolia University,2011.

[13]Mahajan S,Katti J,Walunj A,et al.Designing a databaseencryption technique for database security solution with cache[C]//Proceedings of the 2015 International Advance Computing Conference,Bangalore,India,Jun 12-13,2015. Piscataway,USA:IEEE,2015:357-360.

[14]Shmueli E,Vaisenberg R,Gudes E,et al.Implementing a database encryption solution,design and implementation issues[J].Computers&Security,2014,44(2):33-50.

[15]Zhou Xing,Liu Jun.A novel efficient database encryption scheme[C]//Proceedings of the 9th International Conference on Fuzzy Systems and Knowledge Discovery,Chongqing,China,May 29-31,2012.Piscataway,USA:IEEE, 2012:1610-1614.

[16]Sarfraz M I,Nabeel M,Cao Jianneng,et al.DBMask:finegrained access control on encrypted relational databases [C]//Proceedings of the 5th ACM Conference on Data and Application Security and Privacy,San Antonio,USA,Mar 2-4,2015.New York:ACM,2015:1-11.

[17]Sun Xiaohan.A secure scheme of key management for database encryption[M]//Advances in Technology and Management.Berlin,Heidelberg:Springer,2012:315-319.

[18]Dai Yiqi,Shang Jie,Chen Wei,et al.New key management scheme in database encryption[J].Journal of Tsinghua University:Science and Technology,1995,35(4):43-47.

[19]Xiao Fei,Huang Zhengdong,Wang Guanghua.Key management for database encryption in distributed environment [J].Computer Systems&Applications,2011,20(1):124-127.

[20]Mattsson U T.Key management for enterprise data encryption[J/OL].(2007)[2016-02-26].https://ssrn.com/abstract= 1051481.

[21]Nikooghadam M,Zakerolhosseini A,Moghaddam M E. Efficient utilization of elliptic curve cryptosystem for hierarchical access control[J].Journal of Systems&Software, 2010,83(10):1917-1929.

附中文参考文献:

[3]徐彦彦,徐正全,陈曦.一种基于中国余数定理的等级密钥管理方案[J].华中科技大学学报:自然科学版,2010,38 (12):65-68.

[4]韩心慧,龙勤,司端锋,等.一个基于单向散列函数的实用等级密钥管理方案[J].北京大学学报:自然科学版,2008, 44(4):527-536.

[11]张建民,刘贤德,徐海峰.等级安全系统中的一种新型访问控制方案[J].计算机工程与应用,2007,43(16):156-158.

[12]孙佳思.基于椭圆曲线密码体制的密钥管理方法研究[D].呼和浩特:内蒙古大学,2011.

[18]戴一奇,尚杰,陈卫,等.一种新的数据库加密密钥管理方案[J].清华大学学报:自然科学版,1995,35(4):43-47.

[19]肖飞,黄正东,王光华.数据库中基于密文角色的密钥管理方案[J].计算机系统应用,2011,20(1):124-127.

HU Qianwei was born in 1991.He is an M.S.candidate at College of Computer Science and Technology,Henan Polytechnic University.His research interests include network information security and cryptography,etc.

胡前伟（1991—），男，河南信阳人，河南理工大学计算机学院硕士研究生，主要研究领域为网络信息安全，密码学等。

李子臣（1965—），男，河南温县人，北京邮电大学博士，北京印刷学院教授、博士生导师，主要研究领域为信息安全，电子商务，密码学等。主持或参与了国家973计划、国家自然科学基金等项目的研究工作，发表学术论文40余篇，有20多篇被SCI、EI和ISTP检索。

YAN Xixi was born in 1985.She received the Ph.D.degree in cryptology from Beijing University of Posts and Telecommunications in 2012.Now she is a lecturer at Henan Polytechnic University.Her research interests include networks and information security,digital rights management and digital content security,etc.She published more than 10 scientific research papers,and most of the papers are included by EI and ISTP.

闫玺玺（1985—），女，河南灵宝人，2012年于北京邮电大学获得博士学位，现为河南理工大学讲师，主要研究领域为网络与信息安全，数字版权管理，数字内容安全等。发表学术论文10多篇，多数论文被EI、ISTP收录。

Research on Key Management Scheme for HierarchicalAccess Control in Database*

HU Qianwei1,2+,LI Zichen1,YAN Xixi2
1.College of Information Engineering,Beijing Institute of Graphic Communication,Beijing 102600,China
2.College of Computer Science and Technology,Henan Polytechnic University,Jiaozuo,Henan 454003,China
+Corresponding author:E-mail:huqianwei908@163.com

This paper presents a key management scheme based on elliptic curve cryptosystem to solve the problem of rights management among hierarchical users and access the encrypted database.In the proposed scheme,each user can independently choose own user key,and securely transfer it to trusted center.The trusted center calculates the relational parameters of the user having the partially ordered relation by using the elliptic curve cryptosystem after collecting the secret key parameters.The higher-privileged class will have the right to derive the key information created or owned by a user in a lower-privileged class,and then take advantage of it to decrypt the encrypted database which is also created by the lower-privileged class.The update method of the encrypted database is also considered after the partially ordered relation is changed.Experiments show that key generation,key derivation and access database have high efficiency and security.

was born in 1965.He

the Ph.D.degree from Beijing University of Posts and Telecommunications.Now he is a professor and Ph.D.supervisor at Beijing Institute of Graphic Communication.His research interests include information security,electronic commerce and cryptography,etc.He published more than 40 papers,and more than 20 papers are included by EI,SCI and ISTP.

A

TP393

*The National Natural Science Foundation of China under Grant Nos.61300216,61370188(国家自然科学基金);the Science and Technology Research Project of Henan Province under Grant No.132102210123(河南省科技攻关项目);the Doctoral Funds of Henan Polytechnic University under Grant No.B2013-043(河南理工大学博士基金);the Science and Technology Key Project of Beijing under Grant No.KZ20150015015(北京市自然科学基金重点项目B类);the Science and Technology Project of Beijing Municipal Education Commission under Grant Nos.KM201510015009,KM201410015006(北京市教委科技计划项目);the Natural Science Foundation of Beijing under Grant No.4142016(北京市自然科学基金).

Received 2016-04,Accepted 2016-10.

CNKI网络优先出版:2016-10-18,http://www.cnki.net/kcms/detail/11.5602.TP.20161018.1622.002.html

Key words:encrypted database;key management;elliptic curve cryptosystem;partially ordered relation;user hierarchy