非完整数据库Skyline-join查询*
鲍斌国,秦小麟,李星罗,张 彤
南京航空航天大学 计算机科学与技术学院,南京 211106
1 引言
随着数据库的发展,如何有效精准地从大数据集中获取有价值的信息作为用户决策的参考已经成为一个研究热点。给定一组数据项,Skyline查询[1]旨在得到不被其他数据支配的数据项集合。其中,一个数据项p支配数据项q,当且仅当p在所有维度上优于或等于q,且至少存在一个维度p优于q。比如,一个旅客想要在某个区域寻找一个离沙滩近且价格低的旅馆,这种情况下Skyline 查询只会返回那些不被支配的旅馆。在不失一般性的情况下,假设较低的值对于所有维度上的所有用户都是较优的。Skyline查询的主要目标是为用户提供有价值的参考,由于其重要性,近些年来已经得到了广泛的研究[2-4]。这些算法主要是基于完整数据库的,但这并不能覆盖所有真实的应用场景。
考虑一个来自电影评分应用的真实数据集Movie-Lens。该数据集中每个数据项中包含多个观众对于电影评分的维度。但事实上,一个用户仅评价那些他看过或了解的电影,因此数据项可能会在多个维度上存在数据缺失的情况。传统的Skyline查询无法处理这种数据缺失的数据集,因此Khalefa 等[5]提出了一种非完整数据库中Skyline 查询的定义,各个数据项仅在它们都不缺失数据的维度上进行比较。如表1所示,O1和O2只能在第一个维度上进行比较,因此O1支配O2。之后的许多非完整数据库研究[6-9]是基于该工作的。
但是传统的非完整数据库Skyline查询明显有以下两个缺点:(1)支配传递性的丢失。这不仅大大增加计算量,因为不得不对所有数据进行两两比较,而且会使Skyline查询结果过少甚至是空集。(2)一些非正常的数据项出现在结果集中。比如仅有极少维度数据完整的数据项,它们难以为用户提供有效的选择。这些缺点都会严重误导用户的选择。
对于传统非完整数据Skyline查询的缺点,Zhang等[10]提出了非完整数据库概率Skyline。他将数据项之间的支配关系用概率值表示,最后的Skyline 结果集取最不可能被支配的前K个数据项。但是传统Skyline查询大多假设数据项所有属性均存储在单个关系中,然而实际应用场景经常会涉及到多表连接操作。若盲目地先对所有关系进行连接操作,那么可能会产生海量的数据项,从而导致Skyline 查询效率低下的问题。
因此提出了PSkyline-join算法,该算法主要有四个步骤:对于单个关系中的数据项进行多层次分组;确定每组的局部Skyline 结果集;采用剪枝策略连接局部Skyline结果集;确定全局Skyline集合。本文的主要贡献如下:
(1)对概率Skyline 的定义进行补充使其适用于多表连接Skyline查询。
(2)提出了PSkyline-join 算法,通过多层次分组高效计算局部Skyline候选集。
(3)利用局部Skyline 概率上界与全局Skyline 概率下界剪枝策略去除了无用的Skyline 概率计算,大幅提升了算法效率。
本文的组织结构如下:第2章介绍了非完整数据库Skyline 查询的相关工作;第3 章给出了非完整数据库及概率Skyline 的基础定义;第4 章详细介绍了Skyline-join 的算法流程,包括多层次分组及两种剪枝策略;第5 章通过实验评估了该算法性能;第6 章总结全文。
2 相关工作
关于非完整数据库中的Skyline 查询最早由Khalefa 等[5]提出,文献给出了一种非完整数据库中Skyline 查询的定义,即两个数据项仅在它们都不缺失数据的维度上进行比较来得出支配关系。同时也提出了Bucket 和ISkyline 算法以计算非完整数据库中的Skyline查询结果集。
Bucket算法基于数据项的位图,即数据在某个维度上未缺失数据记为1,若缺失数据则记为0,将所有数据项根据位图进行桶划分;然后确定每个桶的局部Skyline 候选集;最后根据所有桶的局部候选集得到全局Skyline 结果集。ISkyline 在Bucket 算法的基础上添加了更多剪枝策略,从而优化了原算法效率。后来几乎所有的非完整数据Skyline查询研究都基于该工作。Bharuka 等[6]提出了一种基于排序的Bucket 算法(sorted bucket algorithm,SOBA),该算法在桶层次及点层次对数据项进行排序,从而减少了桶之间的数据项比较。
但是基于传统非完整数据库Skyline的算法面临着循环支配的问题,丢失了完整数据库下的支配传递性。对于表1 的数据集,O1支配O2,O2支配O3,按照在完整数据库下的传递性O1支配O3,但此处O3支配O1,因此这三个数据项形成了循环支配。这会导致Skyline查询结果过少甚至是空集。对于上述定义存在的缺陷,Zhang等[10]提出了非完整数据库概率Skyline的概念。概率Skyline将数据项之间的支配关系用概率值表示,最后的Skyline 结果集取最不可能被支配的前K位数据项。同时提出了PISkyline 算法,采用两种剪枝策略和排序技术来加速Skyline 概率的计算。但该研究仅局限在单关系,还不能很好地支持多关系Skyline 查询,因此本文扩展了概率Skyline使其适用于多关系Skyline查询。
近些年来Skyline-join方面的主要研究有:Jin等[11]提出了一种基于排序的多关系Skyline 查询算法,但该算法是非平凡的,需要多次遍历每个关系才能得出正确的Skyline 结果集。Sun 等[12]提出了一种基于SaLSa[13]的分布式环境下Skyline-join查询算法,但该算法并不支持提前终止并依赖于每个关系的多个索引。而后Vlachou 等[14]提出了提前终止条件概念,该条件用于确定算法是否已经遍历了足够多的数据项用来生成完整的Skyline 结果集。Awasthi 等[15]提出了KSJQ(K-dominant Skyline join queries)算法以解决多关系完整库中的K支配Skyline查询问题。针对多数据流的Skyline 查询问题,Zhang 等[16]提出了NPSWJ(naive parallel sliding window join)和IP-SWJ(incremental parallel sliding window join)算法。但是这些工作均未涉及非完整数据库。Alwan 等[17]提出了一种非完整数据库下的Skyline-join 算法JincoSkyline算法,但该算法是基于传统的非完整数据库Skyline,返回的Skyline 结果集不符合用户需求,本文基于概率Skyline 的PSkyline-join 算法能够返回具有高参考价值的Skyline查询结果。
3 问题定义
本章主要介绍非完整数据库和Skyline查询的相关定义与概念。
定义1(单关系概率支配[10])对于两个拥有d维属性的数据项p和q∈D,q支配p的概率定义为:

其中,E(p)表示与p完全相等的数据项集合。
为了便于分析,该定义做了如下假设:
(1)所有的数据项之间都是独立的;
(2)数据项各个维度的属性都是独立的;
(3)缺失值是随机出现在各个维度上的。
有了以上假设,当p(i)和q(i)都是缺失值时:
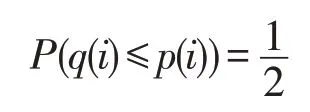
定义1仅考虑了单个关系情形下的概率支配,但当Skyline 查询涉及到多关系时,定义1 假设所有的数据项之间都是独立的,该条件明显不成立,因为连接操作后两个数据项中的部分维度有可能来自同一个关系的同一数据项。因此定义2 对定义1 进行了拓展,使其可以应用于多关系Skyline查询。
定义2(多关系概率支配)对于由多个关系连接而来的数据项p和q,q支配p的定义为:
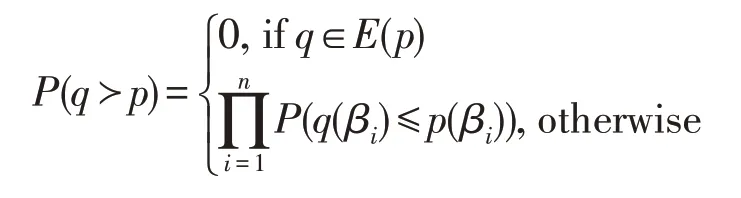
其中,βi表示数据项中来自关系Ri的属性:

由定义2可知,当p和q的部分属性来自同一关系的同一数据项时,这部分属性将不会对支配概率产生任何影响。
定义3(非完整数据下概率Skyline查询)对于一个非完整数据集S,用户指定一个参数K(K>0),概率Skyline查询结果集表示为:

其中:
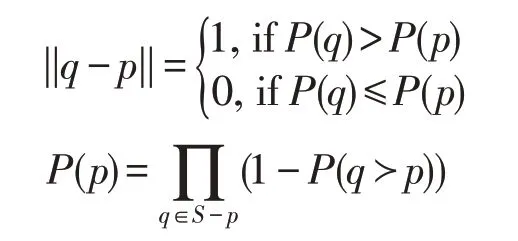
直观上来看,概率Skyline 查询的结果就是Skyline概率排名前K位的数据项,即最不可能被支配的前K个数据项。
考虑表2 中的数据集,用户设置K=2。首先计算每一维度上的概率分布函数
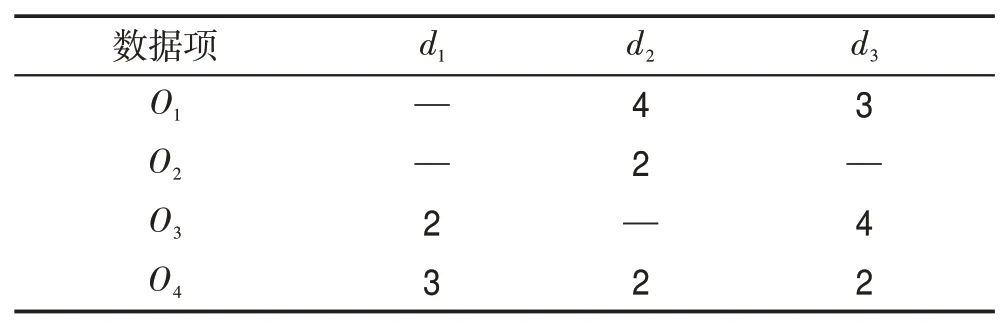
Table 2 Incomplete data set S2表2 非完整数据集S2
4 PSkyline-join算法
如图1 所示PSkyline-join 算法主要有四个步骤:数据项多层次分组;确定局部Skyline概率;连接数据项;确定全局Skyline结果集。
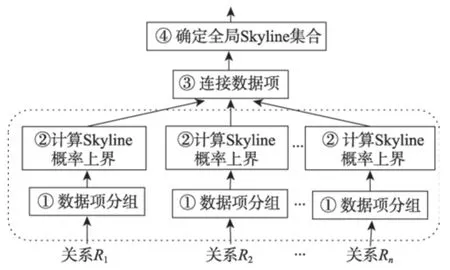
Fig.1 Steps of PSkyline-join algorithm图1 PSkyline-join算法步骤
4.1 数据项分组
第一层分组:对于某个关系将连接键值相同的数据项划分到一组中。第二层分组:在进行上述第一层分组后,再根据数据项的缺失位图对数据项进行二次划分,即桶划分[5]。
考虑例子:对于表3 中的关系R1假设连接键为id,首先将id 值相同的属性项划分到同一组中,表4展示了上述划分结果。然后对于每一组中的数据项根据缺失位图进行桶划分,划分结果如表5所示。
数据项多层次分组主要是为了辅助计算局部Skyline概率上界。
4.2 计算局部Skyline概率上界
对于每个桶中的数据项,仅比较两个数据项都未缺失数据项的维度,从而得到它们之间的支配关系。按照上述支配定义,两两比较桶中的数据项求得每个桶的局部Skyline候选集。表5灰色背景填充的数据项即为局部Skyline候选集。

Table 3 R1data set表3 R1数据集示例
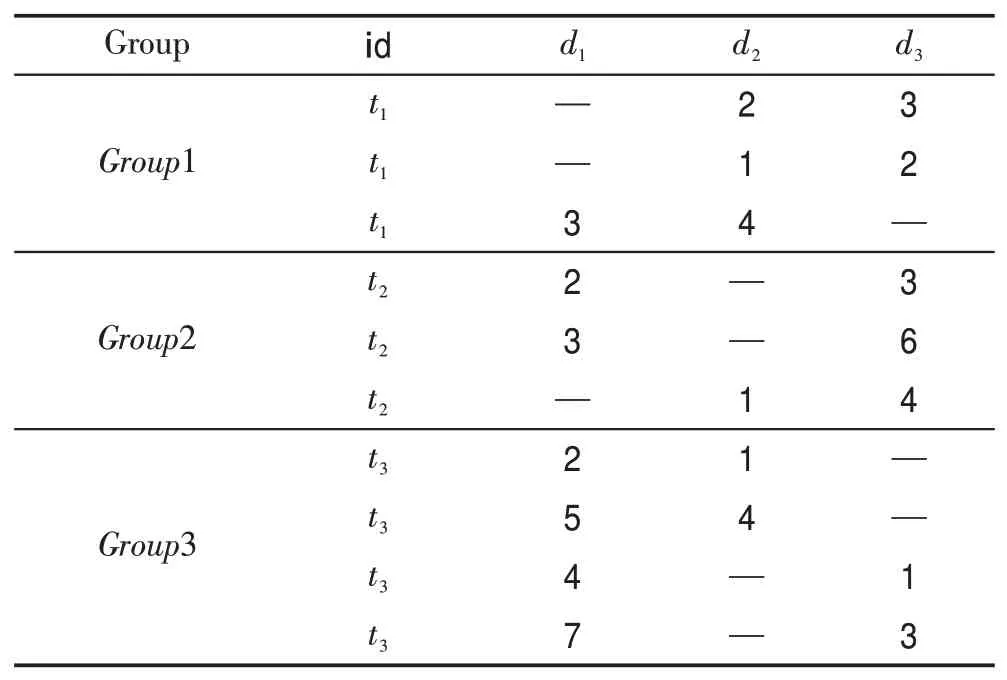
Table 4 R1group dividing表4 R1组划分

Table 5 R1bucket dividing表5 R1桶划分
定理1∀τ1p∈bucket,若∃τ1q∈bucket且τ1q≻τ1p,则∀p≡τ1p⋈τ2p,其Skyline概率上界为,记为:

其中,w表示该桶缺失的维度数量。
证明S={τ|τ≡τ1⋈τ2,τ1∈R1,τ2∈R2},∀p∈S,不妨假设p≡τ1p⋈τ2p,若∃τ1q≻τ1p,则∃q≡τ1q⋈τ2p在各个非缺失维度上支配p,由此:
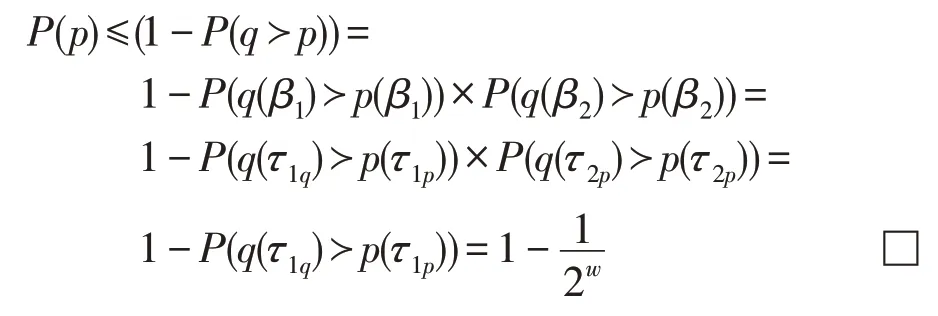
定理1 主要阐明了桶内数据项在与其他数据项连接后所能达到的Skyline概率上限值。同时由定理1可知局部Skyline候选集的概率上界为1。
根据定理1可以设计高效的局部Skyline 概率上界更新算法。算法1 的第1 行对数据项的局部Skyline 概率上界进行了初始化。初始化时假设各个数据项不会被其他数据项支配,因此对各个数据项的局部Skyline概率上界赋值为1。算法第2行至第4行根据连接键值对数据项进行组划分,再根据数据项的位图进行桶划分。为了提高分组效率,可以将数据项的连接键值及缺失位图作为数据项的分组键,再将所有具有相同键的数据项映射到同一集合中。考虑到映射操作的时间复杂度为O(1),可知采用这种分组算法的时间复杂度为O(n),其中n为数据项总数。对于每一个桶中的数据项,将它与桶中的其他数据项进行比较,若桶内没有数据项在非缺失维度上支配该数据项,则将其加入局部Skyline 候选集。由于要两两比较数据项,因此计算局部Skyline 候选集的算法时间复杂度为O(dm2),其中d为数据项维数,m为桶内数据项的数量。算法第8 行,若数据项不为局部Skyline 点,则根据定理1 更新其局部Skyline概率上界。
算法1局部Skyline概率上界算法LocalSkyline-UpBound
输入:非完整数据集S。
输出:各个数据项的局部Skyline概率上界。

4.3 连接数据项
在连接数据项时,除了正常的连接操作外,还需要计算数据项的全局Skyline概率上界。
定理2∀p∈R1⋈R2,p≡τ1p⋈τ2p,其中τ1p∈R1,τ2p∈R2,p的概率上界为:
Psup(p)=Psup(τ1p)×Psup(τ2p)
证明若Psup(τ1p)与Psup(τ2p)均为1,则上式明显成立。若Psup(τ1p)<1 或Psup(τ2p)<1,不失一般性假设Psup(τ1p)<1,Psup(τ2p)=1,由定理1 可知τ1p在与其他数据项连接后的Skyline 概率上限值为Psup(τ1p),故P(p)≤Psup(τ1p),Psup(p)=Psup(τ1p)上式成立。若Psup(τ1p)<1且Psup(τ2p)<1,由定理1证明过程可知∃m≡τ1q⋈τ2p及n≡τ1p⋈τ2q在非缺失维度上支配p,由此得:

定理2 主要阐明了局部Skyline概率上界与全局Skyline 概率上界的关系,从而可以高效地计算数据项的全局Skyline 概率上界,故可以建立高效的剪枝策略。
4.4 计算全局概率Skyline集合
在连接各个关系的数据项后,需要为用户返回全局的Skyline 集合。为了去除不必要的Skyline 概率计算,采用了两种剪枝策略。
剪枝策略1若数据项p在与数据项q比较后,其Skyline概率已经小于全局的Skyline概率下界,则可以中断计算p的Skyline概率。
算法2Skyline概率算法SkylinePro
输入:非完整数据集Q,数据项p,globalLowBound。
输出:数据项Skyline概率。

剪枝策略2若数据项p的全局Skyline概率上界小于全局Skyline 概率下界,则无需计算数据项p的Skyline概率。
算法3PSkyline-join算法PSkyline-join
输入:非完整数据集{R1,R2,…,Rn},Skyline 结果集大小K。
输出:Skyline结果集。
算法3 的第1 行对全局Skyline 概率下界和全局Skyline 结果集进行初始化,由于开始时全局Skyline结果集为空,因此对Skyline概率下界赋值0。算法第2 到3 行对各个数据集的局部Skyline 概率上界进行计算。第4 行将各个数据集进行连接,并根据定理2计算每个数据项的全局Skyline概率上界。第5行根据数据项的全局Skyline 概率上界对数据项进行分类,Q1中的数据项Skyline 概率上界均为1,Q2中的数据项Skyline 概率上界小于1。第6 到8 行对Q1中的数据项进行Skyline概率计算,并更新Skyline结果集和全局Skyline 概率下界。全局Skyline 概率下界更新为Skyline 结果集数据项中最小的Skyline 概率。第9到13行结合剪枝策略2对Q2中的数据项进行Skyline 概率计算。将连接后的数据分类为Q1和Q2的出发点:由于Q1中数据项的Skyline概率上界都为1,因此这部分数据项最有可能进入全局Skyline结果集,并且能够大幅提升全局Skyline概率下界,使得在两种剪枝策略能够发挥更大的作用。尽管存在两种剪枝策略,但最坏情况下所有数据项依然需要进行两两比较,因此算法3的时间复杂度为O(dn2),其中d为数据项连接后的维数,n为数据项连接后的数量。
5 实验及分析
所有的对比算法都使用Python 实现,运行环境为Ubuntu16.04,Intel Core i5-7500 3.4 GHz 处理器,8 GB内存。
由于目前没有符合实验需求的公开数据集,因此实验主要在人造数据集上进行,主要关注两个数据集R1和R2在进行多对多连接操作后的Skyline 查询问题。实验主要有5 个参数:数据集基数、分组基数、数据集维数、缺失率、自定义Skyline 候选集大小K。数据集基数指一个数据集中的数据项的数量。分组大小指每个数据集按照连接键值分组后每组包含的数据项数量。数据集维度指一个数据集的属性维数。缺失率指发生数据缺失的数据单元与所有数据单元的比例。人造数据集的每一维数据均为0,1之间的实数且服从随机分布。
每一组实验主要对比基准算法、PISkyline算法、PSkyline-join 算法处理Skyline-join 查询的性能。其中基准算法为未经任何优化的概率Skyline[10]查询算法,与该算法进行比较可以很好地观察两种剪枝策略对于多关系概率Skyline查询效率的影响。
5.1 数据基数对算法性能的影响
该组实验的具体设置为:R1和R2的缺失率和数据集维度固定为20%和3,Skyline候选集大小K固定为10,R2的数据集基数和分组基数固定为100和10,R1的数据集基数分别为1×103、2×103、3×103、4×103、5×103,R1的分组基数分别设置为100、200、300、400、500。由上述设置可知R1与R2连接后的数据集基数分别为1×104、2×104、3×104、4×104、5×104。图2展示了3 种算法在各个数据基数上的性能。由图2(a)可知PSkyline-join的算法效率最高,其耗时随数据基数线性增长,基线算法耗时随数据基数平方增长。图2(b)展示了概率Skyline 计算涉及到的两两数据项比较次数,由于PSkyline-join 算法的剪枝策略2 是在多层次分组后进行,而非像PISkyline 算法在单层次地进行桶划分后进行剪枝,故而剪枝率不如PISkyline高。图2(c)展示了两种剪枝策略的剪枝率,可以看出随基数增长PSkyline-join 算法总的剪枝率基本不变,但剪枝策略2随数据基数的增长发挥的作用线性增长。
5.2 数据维度对算法性能的影响
该组实验设置为:R1和R2的缺失率固定为20%,Skyline候选集大小K固定为10,R1的数据基数和分组基数固定为1 000和100,R2的数据基数和分组基数固定为100和10,R1和R2的数据集维数分别为2、3、4、5、6。由上述设置可知R1和R2连接后的数据集基数为4、6、8、10、12。从图3(a)可知PSkyline-join算法在各个维度的效率都为最优,由图3(c)可知当维数为8 时PSkyline-join 算法的总体剪枝效率最低,从而造成该维度下的算法效率低下。同时随着维数的上升剪枝策略2 的作用越来越小。因为随着维数的上升单个桶中的数据项数量下降,从而造成其中的数据项被支配的概率变小,局部Skyline 候选集变小。
5.3 数据缺失率对算法性能的影响
图4展示了各个缺失率下各个算法的性能表现。该组实验设置为R1数据集基数固定1 000,R1分组基数固定100,R2数据集基数固定100,R2分组基数固定10,缺失率分别为10%、20%、30%、40%、50%。如图4(a)所示,注意该图y轴刻度为对数型而非线性的,PSkyline-join算法始终表现最优。从图4(b)可以看出PSkyline算法在计算Skyline概率时的两两比较次数略少于PSkyline-join算法,但由于其桶划分是针对连接后的所有数据项,因此在划分并计算概率上界时消耗了大量时间,导致消耗的总时间多于PSkyline-join 算法。图4(c)主要展示了两种剪枝策略的剪枝率,可以看出随着缺失率的增长,PSkylinejoin 算法的总体剪枝率缓慢下降,但剪枝策略2 的作用随着缺失率增长有所提升。
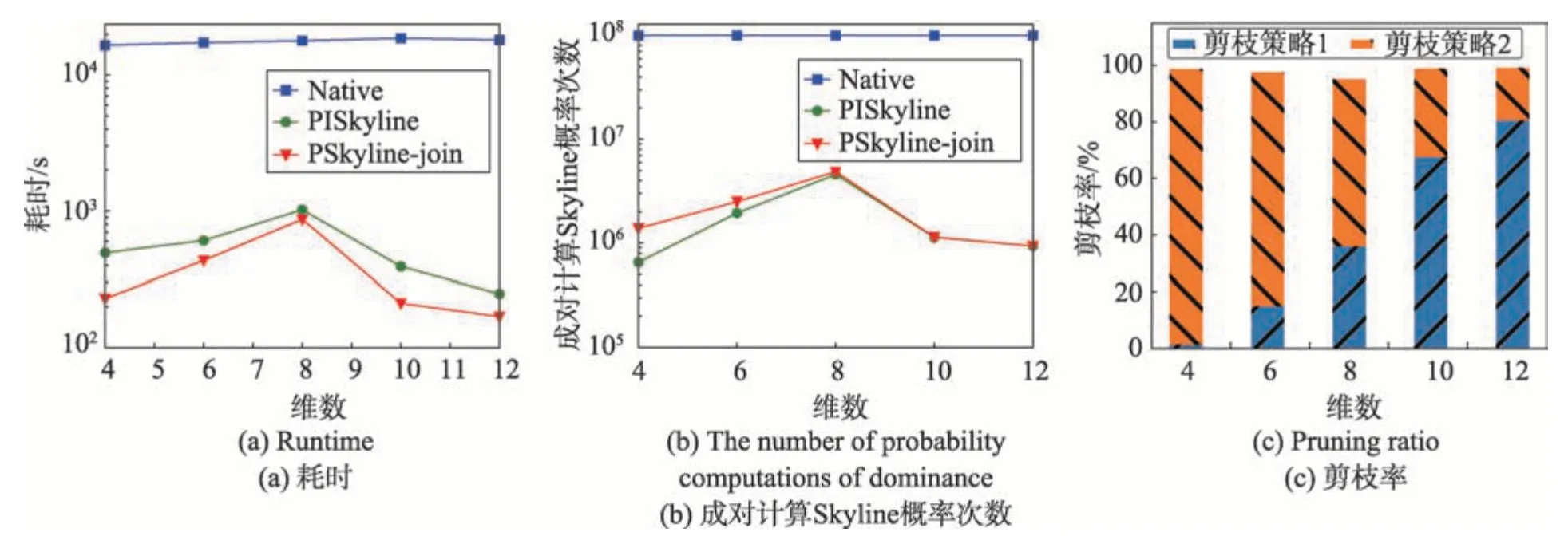
Fig.3 Effect of dimensionality on performance图3 数据维度对算法性能的影响
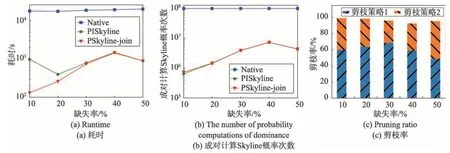
Fig.4 Effect of missing ratio on performance图4 缺失率对算法性能的影响
6 结束语
本文针对非完整数据库下的Skyline-join查询问题进行了深入的分析和研究,提出了一种基于多层次分组的概率Skyline 查询算法PSkyline-join。对单关系下的概率Skyline 进行了补充,使其适用于多关系。PSkyline-join 算法通过多层次分组计算数据项的Skyline概率上界,结合全局Skyline概率下界有效地对Skyline概率计算进行剪枝。当算法结束时为用户返回最不可能被支配的K个数据项,从而满足用户的真实需求。实验证明了PSkyline-join 算法能有效地解决非完整数据库下的Skyline-join 查询,其效率相较未优化算法有着最多百倍的提升。

