卷积特征多伯努利视频多目标跟踪算法*

杨金龙，汤 玉，张光南

1.江南大学 物联网工程学院，江苏 无锡 214122

2.长安大学 信息工程学院，西安 710064

1 引言

视频目标跟踪技术一直是计算机视觉研究领域的热点和难点问题之一，尤其是对数目未知且时变的视频多目标跟踪技术研究，在军事和民用领域都具有重要的意义，相关研究成果已得到广泛应用[1-2]。视频多目标跟踪比单目标跟踪更为复杂，不仅包含视频单目标跟踪中存在的复杂问题，如目标自身旋转、变形、快速运动或相机抖动等导致的模糊、受光照变化的影响、背景干扰等[3-4]，同时还包含视频多目标存在的紧邻和交叉运动，导致目标出现重叠和分裂等相互干扰现象。此外，视频目标的数目也不确定，可能存在新出现目标或目标消失等情况，难以正确区分各个目标。

针对上述问题，学者提出了许多方法，主要可以概括为以下几方面:

（1）基于数据关联的目标检测跟踪方法。通常采用目标检测器对视频序列进行多目标检测，然后借助数据关联等技术完成视频多目标跟踪。典型的数据关联如线性规划（linear programming）[5]、信任传播（belief propagation）[6]、网络流（network flow）[7-8]、图分解（subgraph decomposition）[9]、多假设跟踪（multiple hypothesis tracking）[10]等。虽然这些方法在视频多目标跟踪中取得了一定的效果，但由于复杂的数据关联运算，一定程度上降低了算法的运算效率。

（2）随机有限集（random finite set，RFS）滤波视频多目标跟踪方法。随机有限集理论是解决复杂环境下数目未知且时变多目标跟踪问题的有效理论工具。分别将每个时刻的目标状态和观测建模为独立的随机有限集，借助多目标贝叶斯估计理论递推估计多目标联合状态的后验概率，可有效避免观测与目标之间复杂的数据关联运算。自Mahler[11]提出概率假设密度（probability hypothesis density，PHD）和多目标多伯努利（multi-target multi-Bernoulli，MeMBer）滤波器之后，随机有限集理论在目标跟踪领域得到了广泛的应用。概括来说，基于随机有限集理论的多目标跟踪算法主要包含两大类：基于概率假设密度（PHD）/势概率假设密度（cardinalized PHD，CPHD）的多目标跟踪算法和基于多伯努利（MeMBer）/势均衡多伯努利（cardinality balanced MeMber，CBMeMBer）的多目标跟踪算法。典型的闭合解有：粒子滤波PHD/CPHD、高斯混合PHD/CPHD、粒子滤波CBMeMBer和高斯混合CBMeMBer等及其基于箱粒子（box-PF）、边缘粒子（Rao-Blackwellised particle filter，RBPF）、变分贝叶斯（variational Bayes，VB）等改进算法[12-23]。近年来，尤其是对多伯努利滤波器改进而形成的δ广义标签多伯努利（δ-generalized labeled multi-Bernoulli，δ-GLMB）滤波算法、标签多伯努利（labeled multi-Bernoulli，LMB）算法、泊松多伯努利（Poisson multi-Bernoulli，PMB）滤波算法等[20,24]，在目标跟踪领域中得到了广泛关注。

近几年，虽然随机有限集理论在多目标跟踪领域得到了不断完善，尤其是针对点目标跟踪、扩展目标跟踪等[12-22]，但基于随机有限集滤波算法在视频目标跟踪上的应用还比较少，国内也处于起步阶段。论文主要集中在类似于点目标处理方法，将随机有限集滤波框架推广到视频多目标跟踪中，如文献[25-28]提出在概率假设密度（PHD）滤波框架的基础上实现视频多目标跟踪。文献[29-32]提出在多伯努利（MeMBer）滤波框架的基础上实现视频多目标跟踪，将视频多目标建模为随机有限集的形式，采用粒子或高斯概率假设密度和多伯努利滤波方法进行目标状态提取。文献[33-35]在标签多伯努利（LMB）框架下实现了视频多目标跟踪，考虑多伯努利滤波分量的标记信息，即在跟踪过程中综合考虑视频目标的身份信息，提高了算法对视频目标的跟踪效率。但当视频多目标跟踪过程中出现典型的如目标交叉、紧邻或复杂背景干扰及遮挡时，性能将下降，甚至出现滤波器失效而导致目标漏跟或错跟现象。

针对上述问题，本文在多伯努利滤波框架下，深度分析目标的特征信息，引入抗干扰的卷积特征，提出基于卷积特征的多伯努利视频多目标跟踪算法，并在目标状态提取过程中，进一步提出模板更新策略，使用自适应学习速率进行更新，适应目标的变化，以解决目标紧邻相互干扰的问题。最后，本文进一步引入粒子标记技术，实现了对视频多目标的航迹跟踪。

2 算法基础

2.1 多伯努利滤波原理

多伯努利随机有限集可看作多个相互独立的单伯努利随机有限集X(i)的并集，即，M表示伯努利随机有限集的个数。令r(i)和p(i)分别表示每个单伯努利RFS 中元素的存在概率和概率分布，则多伯努利RFS的概率密度可表示为[21]：

随机有限集可由其概率密度函数进行描述，该集合的平均势估计即为目标数目估计。假设一个参数集可描述一个多伯努利RFS，则多目标多伯努利滤波就是将状态集和观测集都采用多伯努利RFS 近似表示，通过预测和更新步骤递推r(i)和p(i)以实现多目标跟踪。本文算法是在CBMeMBer框架下提出，关于CBMeMBer 算法的具体步骤可参考文献[14]。

2.2 目标卷积特征及量测似然

为了提高提出算法对紧邻目标及存在背景或其他目标干扰的跟踪能力，对目标特征进行深度分析，引入卷积特征[36]对目标进行描述，并在跟踪过程中，融合目标的卷积特征建立似然模型，采用多伯努利标记粒子滤波方法提取目标的状态及其身份标识。卷积特征提取及似然模型建立过程如下。

（1）图像预处理

从视频第一帧中得到目标图像作为输入图像，规范化输入图像的尺寸为n×n（本文为32×32），并转化为灰度图像I，采用大小为w×w（本文为6×6）的窗口滑动。如图1所示，从规范后图像的左上角开始，每次向右滑动1个像素，直到最右边，再回到最左边，向下滑动1 个像素，重复之前过程，直到目标图像的右下角为止，得到目标图像小块的集合y={Y1,Y2,…,Yl}，其中Yi∈Rw×w，l=(n-w+1)×(n-w+1)。然后，对每个小块Yi中的像素减去该小块的均值，以消除亮度的影响，只保留其梯度信息，并做2范数归一化处理。

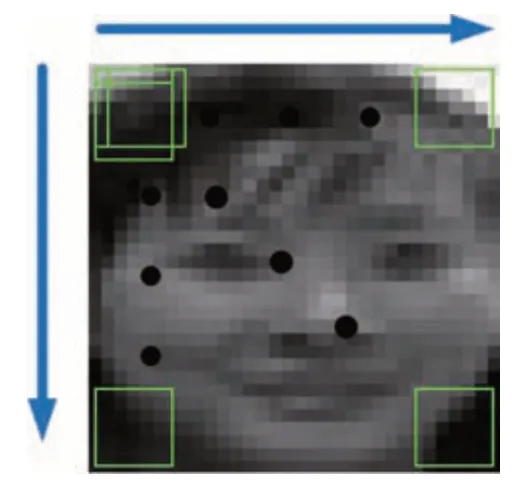
Fig.1 Legend of window slide method图1 窗口滑动方法图例

（2）卷积特征提取

在目标预处理结束后，采用K-means算法[37]选择出d（本文为100）个小块的集合并用第i个小块在图像I上做卷积操作，得到一个目标特征图，其中

为弱化背景的干扰，在目标建模时，先在目标附近采集m（本文为20）个背景样本，背景样本通过将第一帧的目标框做上下平移运动得到，平移的值随机产生，但向左或者向右平移值的绝对值需大于宽和高的1/4，然后对采集的背景样本进行与上述目标图像相同的预处理操作。如图2所示，绿色框为目标的真实位置，蓝色框为采集的背景样本，红色框为真实位置向外扩张1/4 的结果。对每一个背景样本采用Kmeans算法选取d个特征小块，其中，第i个背景样本的特征小块集合为将m个背景样本获得的特征小块进行平均池化操作以生成背景的平均特征小块集合，即最后，将其与图像I做卷积操作，得到背景在图像上的特征图，本文称为背景特征图

Fig.2 Legend of background sample sampling method图2 背景样本采样方法图例

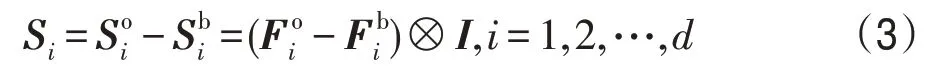
如图3 所示，将得到的d个特征图Si按行展开，成为d个一维向量，并按顺序拼接，最终得到目标的卷积特征c，其中，c∈R(n-w+1)2d。

Fig.3 Legend of convolution feature图3 卷积特征获得图例

（3）稀疏表示特征图

将特征图集S看作三维的张量C∈R(n-w+1)×(n-w+1)×d，基于该张量，可以较好地描述目标，并具有较好的鲁棒性，张量中值越高的地方与目标的某个特征越匹配。因此，通过对张量稀疏化表示[38]来凸显目标的特征，利用稀疏向量c去逼近vec(C)，使式（4）的目标函数最小化：

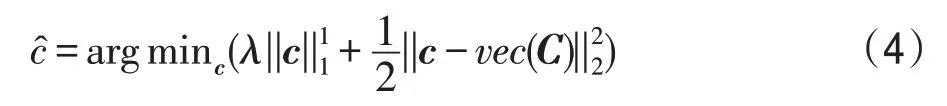
其中，vec(C)是串联C中所有元素的列向量，vec(C)∈R(n-w+1)2d。此外，通过soft-shrinking 方法[39]可求得稀疏表示的唯一解，即：

其中，λ是张量C的中位数。

通过式（4）和式（5）得出的稀疏表示c可凸显目标的主要特征，为此在下文目标模板更新时，将其融合到更新公式中以加强对目标主要特征的描述，以降低非主要特征的干扰。

（4）量测似然建模

在视频跟踪过程中，为了衡量目标模板与候选模板之间的相似度，提出算法中建立如式（6）所示的量测似然模型，其中，ch表示候选目标卷积特征，c为目标的卷积特征，即：

3 视频多目标跟踪算法

在使用卷积特征对目标建立似然模型的基础上，融合到多伯努利滤波框架下，实现对视频多目标的跟踪。首先，采用卷积特征对多个目标分别建立有区分背景能力的特征图，并根据候选目标特征与目标模板进行量测似然建模，采用粒子标记技术[40]滤波，提取目标状态。在对紧邻多目标跟踪时，提出自适应的处理方法，设计自适应目标更新策略，有效提高算法的跟踪精度。提出算法的流程框图如图4 所示，主要步骤和自适应处理方法如下。

3.1 算法步骤

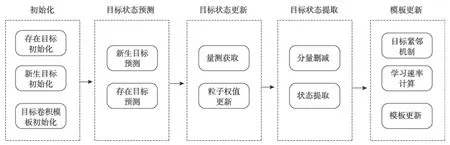
Fig.4 Flow of proposed algorithm图4 算法流程框图

本文采用x=[m,n,w,h]的形式表示目标状态向量，其中m、n、w、h分别为目标跟踪框的左上角横坐标、左上角纵坐标、宽和高。具体算法步骤如下：

步骤1初始化。

步骤1.1存在目标初始化。在初始时刻k=0，对存在目标设置目标状态集，并设置目标的存在概率Ps（实验中设为0.99），其中，M0表示目标的个数。采用第2.2 节描述的方法，提取目标i的卷积特征，并利用粒子滤波技术对目标进行采样。

步骤1.2新生目标初始化。在实际场景中，新生的目标一般出现在固定的范围，根据这个假设，设置新生目标集和新生概率PΓ（实验中设为0.02），其中MΓ表示目标的个数，并提取新生目标i的卷积特征

步骤2多伯努利预测。

根据视频序列的先验信息对存在目标和新生目标进行状态预测。本文采用随机游走模型作为目标的运动模型。即x(k+1)=x(k)+g(k)，其中g(k)为高斯噪声。则存活目标预测后的多伯努利集参数为：

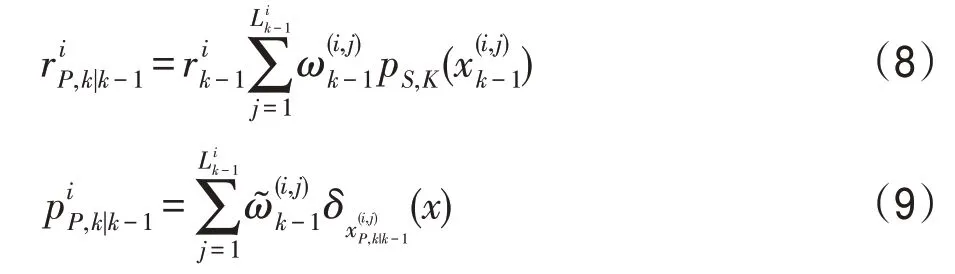
步骤3多伯努利更新。

步骤3.1提取粒子表示的候选目标的卷积特征，计算目标i的第j个粒子与目标i的卷积特征模板的观测似然值g(x(i,j))，即：

步骤3.2更新多伯努利集。通过粒子的观测似然值更新目标粒子多伯努利参数[41]：

步骤4分量删减及目标状态提取。

在每一时刻，目标多伯努利集会随着目标的新生而一直增加，因此对于存在概率较小的伯努利分量（实验中设为小于0.1）认为其不存在，并将其删除，提高算法的效率。对于存在概率大的伯努利分量（实验中设为大于0.5），则根据其更新后的伯努利分量提取其状态。

步骤5模板自适应更新。

3.2 目标轨迹跟踪

对于多伯努利滤波算法无法得到各个目标运动轨迹的问题，本文引入粒子标记技术，通过对比伯努利分量的标记来获得各个目标的完整轨迹。具体标记方法步骤如下：

（1）标记预测。对k时刻的伯努利分量标记的预测Bk|k-1，可以通过新生目标的多伯努利分量的标记BΓ和k-1时刻存活目标的多伯努利分量的标记Bk-1来获得，即：

新生的多伯努利分量标记BΓ可表示为：

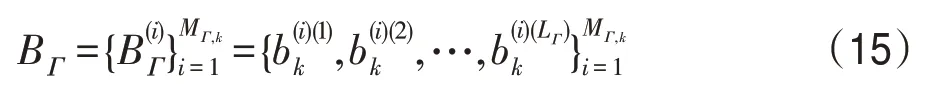
其中，MΓ,k是k时刻新生伯努利分量的个数，LΓ为新生伯努利分量的粒子数。

k-1 时刻存活目标的多伯努利分量的标记Bk-1可表示为：

（2）标记更新。通过预测后的伯努利分量的标记更新量测数据的标记，可以表示为：

其中，|Zk|表示量测的个数，=Bk|k-1,n=1,2,…,|Zk|。

本文中，当多个伯努利分量合并时，合并后的伯努利分量标记选取存在概率较大的伯努利分量的标记。

3.3 模板自适应更新

由于目标在运动过程中，受复杂背景干扰、目标自身扭曲或其他形状变化等，目标状态不断发生变化，如果不对目标模板进行更新，会导致目标跟踪不准确，甚至导致跟踪失败。本文融合当前估计模板和原模板进行自适应更新模板，即[36]：

其中，ρ为自适应学习速率，ct、ct-1分别为t、t-1时刻的目标模板，为t-1时刻对目标跟踪结果的卷积特征的稀疏表示，可以通过式（5）获得，卷积特征的稀疏表示能够凸显目标的主要特征。从式（14）可以看出，通过稀疏表示和原模板结合的更新方法能够增强目标主要特征的重要性，弱化次要特征，使更新后的目标模板能够较好地表示目标。

针对自适应学习速率ρ的取值，本文提出根据目标两帧之间的状态变化和目标之间的紧邻程度进行自适应调整。

（1）自适应学习速率

当目标发生变化时，目标跟踪框的相对位置和大小都会发生相应的变化，因此通过前后帧跟踪框之间的相对位置和大小变化程度可判断目标的变化情况，进而可以设计自适应学习速率。

如图5 所示，绿色跟踪框S1是目标当前跟踪结果，假设红色框S2和黄色框S3为目标下一帧的两种不同跟踪结果。可以看出，黄色框S3较之红色框S2，目标的变化程度较大，如果采用传统的与S1相交部分的面积来表示目标变化程度，可以发现，不管目标框增大多少，相交部分面积始终不变，不能体现目标的变化程度。而本文提出采用与S1不相交部分面积来表示目标变化程度，明显可以看出，S3与S1不相交部分的面积大于S2与S1不相交部分的面积，可以反映出黄色框S3的变化程度比红色框S2的变化程度要大。

Fig.5 Change of target tracking boxes图5 目标跟踪框变化示例

假设第k-1帧目标i的状态为，跟踪框内区域表示为S1，第k帧目标i的状态为，跟踪框内区域表示为S2。图5所示为前后两帧跟踪框重合的情况，假设相邻帧目标跟踪框不相交区域(差异性)为S1,2，即S1,2=S1⋃S2-S1⋂S2，则学习率定义为：

图6 所示为另外两组图像前后帧中目标跟踪框部分重叠情况，图中红色框S1表示上一帧时刻跟踪结果，绿色框S2表示当前帧跟踪结果。图6（a）中，左侧目标减小，右侧目标增大，根据式（19）同样可以获得目标的学习率，从而使模板更新适应目标框大小的自适应变化。图6（b）中，左侧目标移动速度快，对应不相交部分面积会较大，右侧目标移动速度慢，对应不相交面积会较小。因此，根据式（19），左侧目标的学习率会大于右侧的学习率，从而可以使得模板更新适应目标的运动快慢。

（2）紧邻目标自适应更新机制

多目标交叉运动或其他紧邻目标运动时，可能会存在一个目标被另一个目标遮挡（或部分遮挡）。如图7 所示，如果遮挡程度较大，则剩余目标特征将不足以描述真实目标，仍然进行模板更新，可能会导致模板被恶化，难以有效估计目标的状态，甚至导致后续目标的跟踪失败。因此，对紧邻目标，提出算法将进行自适应判断，根据目标相交（干扰）程度θ来确定是否需要更新模板。

Fig.6 Target tracking boxes before and after frames图6 前后两帧目标跟踪框

假设k时刻，目标i的状态为，其跟踪框内区域为S1，目标j的状态为，其跟踪框内区域为S2，假设目标1 和目标2 跟踪框相交的区域为S3，即S3=S1⋂S2，则两个目标的相交（干扰）程度定义为：

当目标相交程度θ大于设定阈值时，则目标模板不更新，否则进行自适应更新，实验中阈值为θ=0.2。

图7为两个目标交叉运动示意图，两个目标分别经历了紧邻、重叠和分离过程，图中红色框S1为左侧目标跟踪框，绿色框S2为被遮挡目标的跟踪框，S1与S2的相交区域为S3。如图7（a）所示，当红色框的目标接近绿色框的目标时，相交区域S3就会逐渐增大，根据式（20）得到的相交程度θ也会随着增大，说明目标相互干扰程度在增大。当增大超过设定的阈值时，则对目标的模板不予更新，降低干扰的程度。如图7（c）所示，当两个目标相互分开时，跟踪框的相交区域S3会逐渐减小，相交程度θ随着减小，即目标相互干扰程度减小，当减小到设定的阈值时，对目标模板恢复自适应更新机制。

4 实验结果及分析

本文选择3组数据进行实验，用于验证提出算法在目标尺寸变化、目标紧邻、目标数目变化等情况下的跟踪性能。其中，实验1 为公共标准数据库Terravic Research Infrared Database[42]中的一组红外视频序列图像，实验2 和实验3 分别为标准的CAVIAR 数据库[43]中两组彩色序列图像，并采用最优次模式分配（optimal subpattern assignment，OSPA）距离统计[44]和目标数目估计两个指标，分别对提出算法和基于直方图的多伯努利多目标跟踪算法[41]进行性能对比分析。算法中的参数设置如下：

目标生存概率Ps=0.9，新生目标概率PΓ=0.02，采样粒子数目最小为Lmin=100，最大为Lmax=600。

4.1 实验1

本组实验中，涉及到目标尺寸变化问题。左侧目标向左移动，并且目标尺寸逐渐缩小，右侧目标向右移动，目标尺寸逐渐变大。

图8分别给出了文献[41]和本文提出算法的跟踪结果图，可以看出，文献[41]中算法能够跟踪上目标，但无法适应目标尺寸的变化，在120 帧和150 帧时，右边目标只能被跟踪一部分，跟踪框不能完全包含目标，而左边目标的跟踪框包含过多的背景信息；提出的算法由于考虑了目标的卷积特征，并采用自适应的模板更新策略，取得了较好的跟踪效果。

4.2 实验2

本组实验场景为具有出入口的交叉通道，涉及到目标新生、目标消失、目标尺寸变化和目标交叉运动等复杂问题。

Fig.8 Tracking results of the first experiment图8 实验1跟踪结果

图9分别给出了文献[41]算法和提出算法的跟踪结果。可以看出，在70到130帧之间，位于图中心的两个目标被左侧出现的目标遮挡，文献[41]的算法不能区分交叉运动的目标，当两个目标紧邻时，被误跟为一个目标，导致目标被漏跟踪；而本文提出算法，因为采用的卷积特征能够区分不同目标，并根据紧邻目标机制，在目标相互遮挡过程中自适应停止模板更新，避免模板被错误更新，从而在整个跟踪过程中能够准确地跟踪每个目标。

4.3 实验3

本组实验中，涉及目标新生、目标消失、目标靠近、光照变化、目标尺寸变化等复杂问题。实验中包含4 个目标，每个目标都经历从新生到消失的过程，目标特征和大小一直发生变化，且目标之间也相互紧邻干扰。

图10 分别给出了文献[41]算法和本文提出算法的跟踪结果。可以看出，文献[41]算法中，当目标紧邻时会出现目标合并，导致目标漏跟，并由于没有考虑模板自适应更新机制，不能适应目标特征的变化，导致目标跟踪失败。提出算法中，由于考虑目标的卷积特征，并设计了自适应的模板更新机制，能较好地适应目标特征的变化，因此获得了较好的多目标跟踪效果。

图11给出了3组实验的OSPA距离统计，可以看出，提出算法采用卷积特征表示和模板自适应更新机制，OSPA 统计距离明显要低于文献[41]算法。图12 给出了3 组实验的目标数目估计结果，可以看出，本文提出算法能够在复杂环境下准确估计目标的数目，而文献[41]算法因不能区分相似目标和运动变化而导致目标被错跟和漏跟。

Fig.10 Tracking results of the third experiment图10 实验3跟踪结果

5 结论

针对复杂环境下，数目未知且变化的视频多目标跟踪问题，提出一种基于卷积特征的多伯努利跟踪算法，引入K-means 训练的卷积特征，并融合目标和背景的特征信息，构建具有背景识别能力的似然模型，采用粒子标记技术实现对视频多目标的跟踪；针对目标尺寸变化和目标紧邻问题，算法中提出模板自适应更新策略，可以有效地提高算法对复杂环境下视频多目标的跟踪能力，具有一定的实际工程应用价值。

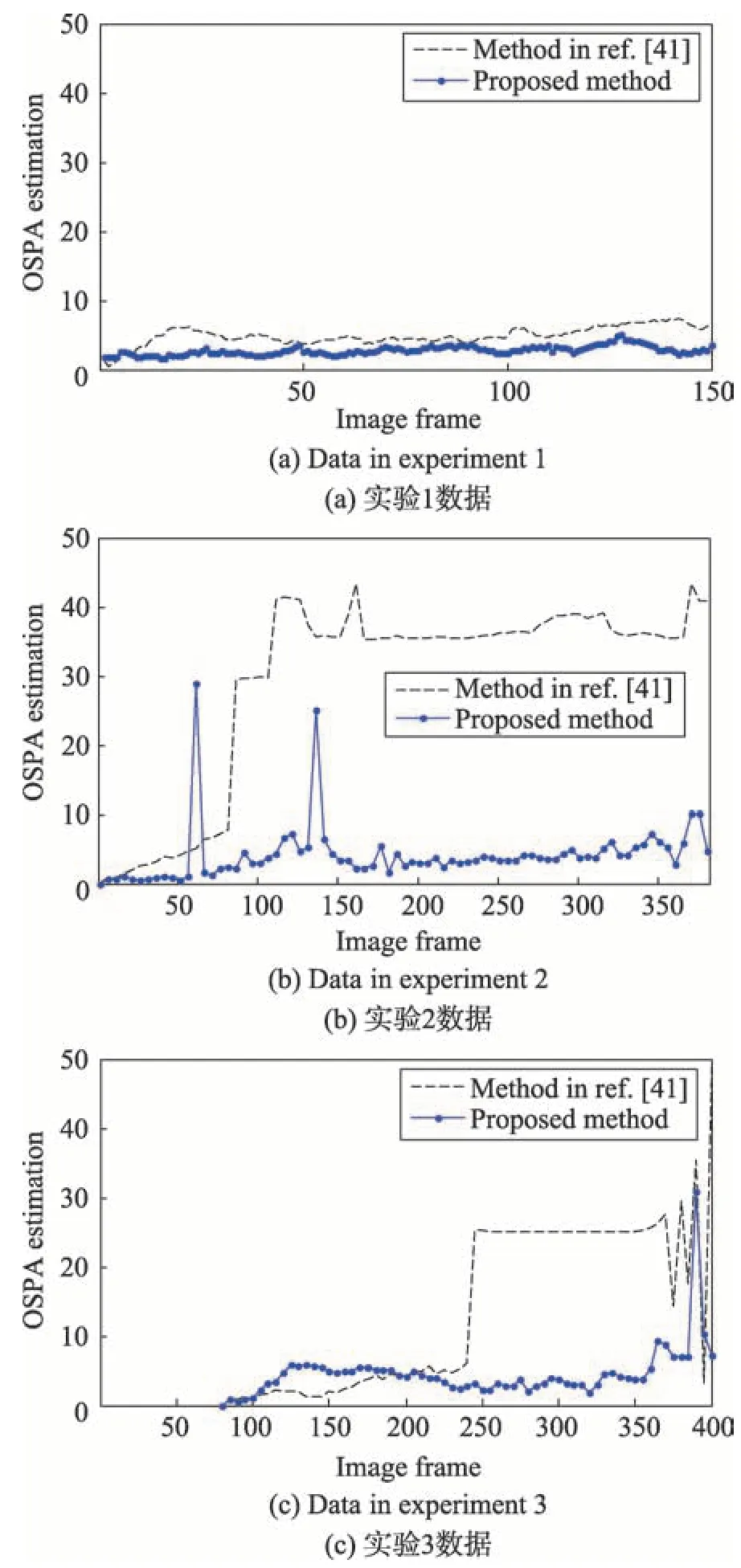
Fig.11 OSPA estimation of 3 experiments图11 3组实验的OSPA精度统计

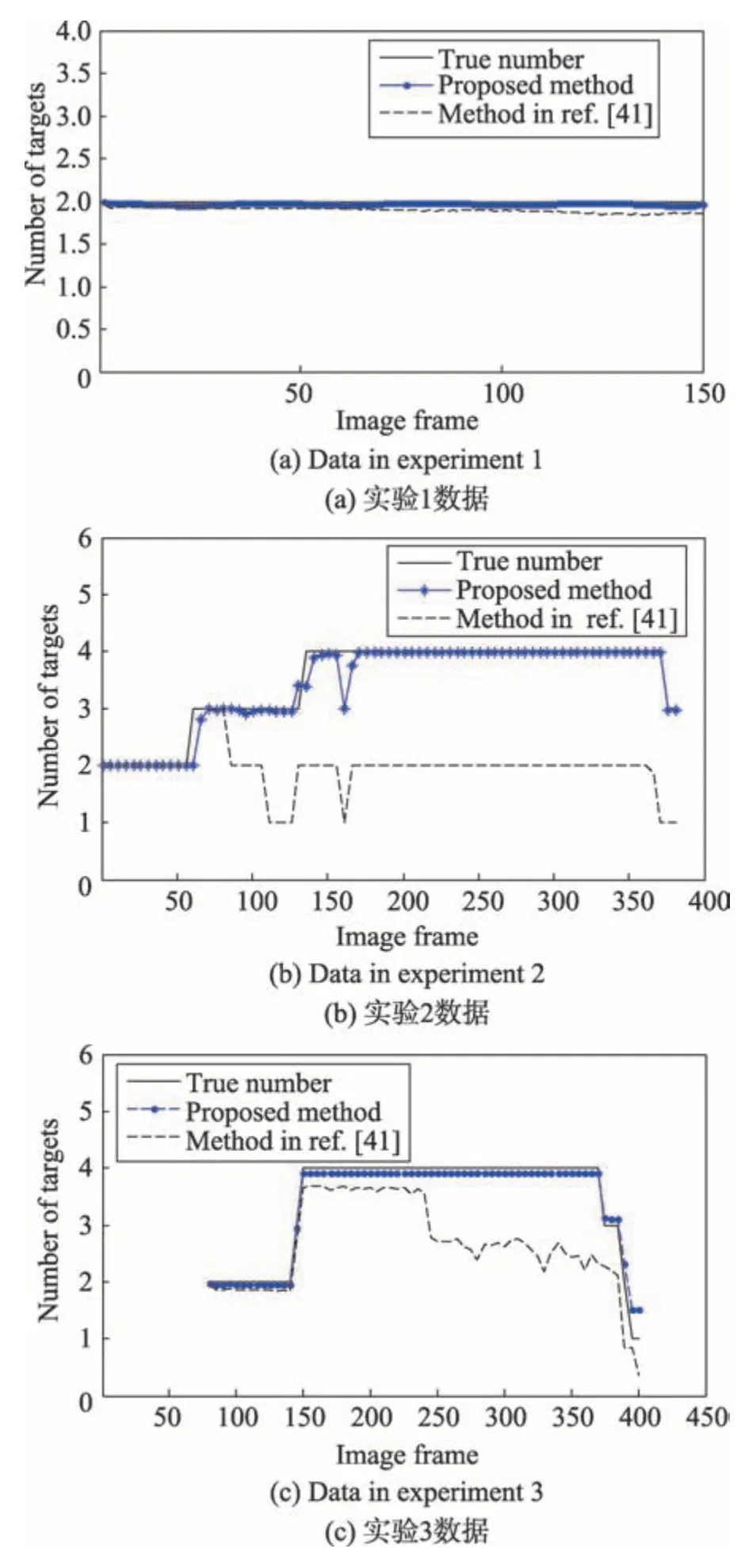
Fig.12 Target number comparison of 3 experiments图12 3组实验目标数对比图