分类处理伺机巧用

吴敏飞

【摘 要】课堂生成性资源从产生的形态上看，可以分为“问题式”和“结论式”两大类。要有效把握这些资源并得以充分利用，必须加以分类处理，并寻找到合适的时机巧用，在应对“问题式”生成资源时，教师可以因势利导，进一步激发学生的学习热情；而在处理“结论式”生成资源时，则可以引发学生进行思辨，从而加深对教学内容的正确理解。由此，数学课堂教学才能变得有效和丰富多彩。

【关键词】问题式生成资源 结论式生成资源 应对策略

根据课堂生成性资源产生的形态，我们可以把其分为“问题式”和“结论式”两大类。“问题式”生成资源指学生在学习过程中产生了新旧经验间的矛盾冲突时，主动提出的问题，这些问题往往更具动态性、深刻性和创新性，是弥足珍贵的课堂动态资源。根据“问题型”生成资源的问题指向性，我们又可将其细分为“发问型”生成资源和“质疑型”生成资源。“结论式”生成资源指学生在经历了学习模型的建构后，结合自身的认知对知识进行重组，主动得出的和新知相关的某个结论。从“结论式”生成资源的正确性来区分，又可以细分成“正向型”和“错误型”。在应对“问题式”生成资源时，教师可以因势利导，进一步激发学生的学习热情；而在处理“结论式”生成资源时，则可以引发学生进行思辨，从而加深对教学内容的正确理解。下面，笔者就课堂教学中常见的几类生成性资源及应对策略进行例谈。

一、问题式生成资源应对策略：因势利导，激发兴趣

（一）“发问型”资源——将计就计

思维从问题开始，有问题才有思考。教师应该充分利用儿童好奇心强的特点，培养学生的问题意识，使他们敢疑敢问，积极地参与到认知活动中，自己去发现问题，提出问题，解决问题。

【案例1】

例如，笔者执教的“确定位置”一课，临近结束时出了点小小的意外：在邀请同学们到我们学校来做客时，大家都很高兴地响应，唯独有个小男孩嘀咕道：“我从没有去过溪口，怎么找得到你们学校呢？”当时大多数学生没有听到他的话，笔者本可以顺利转入下一个练习环节，但是这名同学的嘀咕声却让笔者灵机一动：何不将计就计，让同学们用今天学会的知识来解决这个实际问题呢？

于是，笔者在黑板上的格子图内出示了溪口小学附近的地图（如下图），然后让学生思考并讨论下面三个问题：①溪口小学在地图上的位置是（ ， ）。②图上还有哪些建筑物？它们分别在什么位置？③同学们如果想去溪口小学，在汽车站下车后，可以怎么走？

问題一出示，学生们热情高涨，在讨论中明确了去溪口小学的多条路线。如此一来，既帮助那位男孩解决了难题，又巩固和应用了“用数对确定位置”的知识，真是一举两得。

像这种学生的课堂发问可遇而不可求，值得我们去深入地挖掘与好好利用。面对学生的“发问”，教师不妨“将计就计”——对学生产生的问题进行梳理，并对其进一步挖掘，随机调整教学思路，因势利导，以变应变，不断激发学生的学习兴趣。

（二）“质疑型”资源——抛砖引玉

质疑是探索知识、发现问题的开始。现代教学提倡学生主动发现问题，提出问题，学会质疑问难，进而分析和解决问题。因此，教师应以学生质疑为突破口，捕捉一闪即逝的智慧火花，甚至是“灵感”，及时给予肯定，从而调动起学生学习的积极性。

【案例2】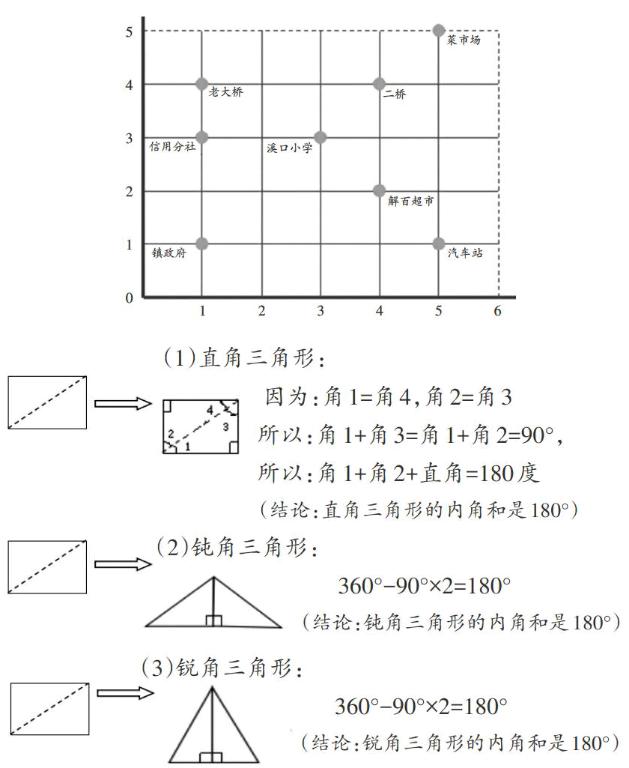

例如，一位教师执教的“三角形内角和”一课。在学生通过“量一量”“折一折”“拼一拼”等方法得出“三角形的内角和是180度”这个结论后，因为课前学生对三角形的内角和是不是180度有疑问，所以教师再次发问：“现在你相信三角形的内角和是180度了吗？”本以为学生会心服口服，没想到还有学生一脸疑惑地说：“老师，刚才我们只是验证了几个三角形的内角和，是不是所有三角形的内角和都是180度呢？”问题一出，全场哗然。台下听课教师也纷纷议论，不知该教师会如何收场。上课教师面对这突如其来的质疑略一思索，马上话锋一转：“我们可以利用以前学过的图形来验证。”随后，他在黑板上出示了一个长方形，提问：“长方形的内角和是几度？”学生异口同声地回答：“360度。”“那我们就利用长方形来小组合作研究一下三角形的内角和。”学生一番操作和讨论之后得出如下结论：

经过这一番由一般到特殊，再由特殊到一般的探究的过程，每名学生都对这个结论不再怀疑，真庆幸这位教师没有放弃这个绝好的教学时机，更要感谢这个来自课堂的异样声音，是它让这节课增添了未曾预约的精彩。

不同的学生在学习同一内容时，常常会因为认知的差异而表达出不同的见解，这种充满“质疑”的问题往往容易给学生带来探究的冲动，教师可采用“抛砖引玉”之计——运用自己的教育机智和胆略，应对学生的质疑，把问题抛还给学生，引导学生带着疑问去探究、证明，从而形成正确的认知。

二、结论式生成资源应对策略：引发思辨，加深理解

（一）“正向型”资源——锦上添花

陶行知曾告诫我们：“我们发现了儿童有创造力，认识了儿童有创造力，就须进一步把儿童的创造力解放出来。”学生的世界充满奇思妙想，在数学课堂里也不乏学生对某个认识内容产生创造性的解决方法。

【案例3】

数学课上，笔者在讲解“角的度量方法”。当在黑板上示范“怎样用量角器量角”时，突然听见台下有同学窃窃私语声 ：“老师，我们有个方法比你更简单！”

“真的吗？说来听听。”笔者饶有兴趣地说。

“你说为了让角的边和量角器的刻度对得更精准，要先把角的一条边延长，这样太麻烦了！（事后笔者在批改作业中发现学生画延长线时易画歪，反而令量的度数偏差更大）我认为可以直接把直尺放在量角器上，把角的边和量角器上的刻度对准，就可以读出角的度数了。”

笔者马上请这两位同学上台演示操作方法，并让台下的学生通过两种方法的比对来评判是否可行。通过操作后，大部分同学都表示认可这种自创的方法，后来的教学实践也证明：采用这种方法量角易操作且正确率高。

学生的思维异常活跃，在课堂上，他们奇思妙想，常常会出现许多创意型结论，我们应及时捕捉放大，使其为数学课堂锦上添花。

（二）“错误型”资源——妙手回春

在教学时不管教师怎样避免，学生仍然会出现这样那样的错误。我们要以平和的心态对待学生的错误，并能独具慧眼，善于捕捉稍纵即逝的错误型生成资源，使“错误”巧妙地服务于教学活动。

【案例4】

在学习了简便计算354-199时，笔者发现许多学生这样进行计算：354-199=354-200-1=153。笔者并没有急于指出这是错误的做法，而是引导学生进行验算，通过验算学生发现这样计算是错误的，可还有学生表示不理解，觉得自己原来的做法是有道理的，199不就是200-1吗？计算结果怎么会错？以上简便计算过程中应用的减法运算性质，对学生来说是很抽象的，如果不是自己反省过来，此类计算对他们而言还是稀里糊涂。于是筆者组织学生先回顾刚才的计算过程，想清楚每一步计算的依据，再分析探究错误的原因。经过反思，学生从不同角度找出了错误的原因。

（1）把354-199改成354-200-1相当于减去了201，正确的应该是354-（200-1）。

（2）354-199改为354先减200，是多减了1，应该要加回来，算式变成354-200+1才对。

（3）举例说明：买东西的时候，如果要付199元，拿出200元，还得找回1元……

通过这样的找错、改错，学生再计算此类算式时，错误的概率大大减少。

当课堂上出现“错误型”生成资源时，我们教师要适时抓住学生的“歪理”，引导学生进行探索，“请”出真理。让学生在体验争议、交流、演绎、推敲等思辨过程的同时，深化对知识的理解和掌握，拓宽思维空间，训练思维的灵活性和创造性，从而达到“妙手回春”之功效。

从上述例子中，我们不难发现， 面对课堂上出现的各类生成性教学资源，教师应把握契机，厘清差异，区别对待，合理利用。这样，一方面可以为学生提供更广阔的思维空间；另一方面可以大大激发学生参与学习的热情，使学生将更多的个人经验融入学习中，使数学课堂教学更加丰富多彩。

参考文献：

[1]陈小丽.动态生成：无法预约的精彩[J].新课程（下），2011，（04）.

[2]周新建.如何处理小学数学课堂中的动态生成[J].小学时代， 2009，（11）.

（浙江省衢州市龙游县溪口小学 314000）