凸显区别多种视角

◇徐文艳

凸显区别多种视角

◇徐文艳

编者按：乘法分配律和乘法结合律相混淆，这是小学数学教学中的一个难点。如何破解这个难题？下面呈现的是部分教师的一些做法，这些案例或许能给您一些启示。如果您赞同，不妨在自己的教学中实践一番；如果您有异议，何不以此为课题开展小研究？讨论无期限，研究永相伴！

在学习加法、乘法的交换律和结合律时，学生很少产生混淆，如用简便方法计算25×（8×4）时的正确率很高。但当学了乘法分配律之后，经常有学生误用乘法分配律，将上式算成25×8+25×4。

这其中的“症结”何在呢？笔者结合自己的教学实践，阐述一下自己的观点和做法。

一、凸显区别，防患于未然

以往大家比较注重在学完乘法分配律之后，提供对比题组，进行辨析，帮助学生进行区分，却没有想到“防患于未然”：在引进乘法分配律时，就要让学生明白它的特殊性。那么，怎样凸显分配律的特殊性呢？

1.复习引入。

我们已经学了加法、乘法的运算规律，用字母表示：

加法交换律________，加法结合律________，适用于________运算；

乘法交换律________，乘法结合律________，适用于________运算。

那么，加法和乘法之间有什么运算规律呢？

2.试一试。

（12＋8）×6=_______，12×6＋8×6=_______。

它们是得数相等的两个算式，可以用等号连起来：

（___＋___）×___=___×___＋___×___。

你能再写出几个这样的算式吗？

（___＋___）×___=___×___＋___×___。

3.归纳。

你发现了什么规律？能总结出来吗？

实践表明：一开始引导学生在系统背景下展开学习，新授时强调这点，以凸显分配律与交换律、结合律的实质区别，有利于发挥先入为主的认知优势，有效促进分配律与前面四种运算定律的精确分化，将后边的干扰消除于萌芽状态。

二、多种视角，解释规律

在教学中，既要注重外形结构，更要注重内涵理解。通常有三种理解方式，在此，以“乘法分配律”为例。

1.调动经验。

学生通过不完全归纳法得到结论之后，教师可让学生回忆一下，有哪些实际问题用到了乘法分配律。把教学的内容与学生的生活实际联系起来，激活学生的生活经验，用“事理”来说明、解释规律，帮助理解。

如：学校购买校服，上衣每件25元，裤子每条35元，买8套，一共需要多少元？由此可知：（25+ 35）×8是先求1套衣服的价格，再求8套的总价；而25×8+35×8是先分别求8件上衣和8条裤子的价格，再相加求总价，因此得出（25+35）×8=25× 8+35×8。

2.借助直观。

在学生得出规律之后，也可以借助几何直观，让学生经历数与形的对应过程，加深理解。如下图：

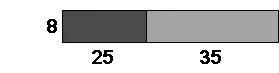
大长方形的面积既可直接用长×宽，也可以分别求出两个小长方形的面积再相加，因此也可以得出（25+35）×8=25×8+35×8。

3．算理解释。

除了现实问题与几何直观相结合，还可以启发学生根据乘法的意义说明规律。如：13×2＋13×4＝13×(2＋4)。

根据乘法运算的意义：（13＋13）＋(13＋13＋13＋13)＝13×6，即2个13加4个13等于6个13。这样就通俗易懂了，既便于学生理解和记忆，也有利于学生灵活运用。

（作者单位：上海市第一师范学校附属小学）