以思维为核心的数学素养导向——基于课堂教学的视角

◇许卫兵

以思维为核心的数学素养导向
——基于课堂教学的视角

◇许卫兵

近来，关于核心素养的讨论成为热点。“由传统知识结构为核心转向以素养发展为核心的过程，其中蕴含的是人类自身发展的心路历程。它的发展暗合某种规律。规律，等待我们去揭示和反思。”[1]这在一定程度上表明，关注核心素养培养已经成为当前和今后一段时间深化教育教学改革的方向。

一

数学是十分重要的基础学科，数学学科的核心素养是什么呢？

我认为，作为一种“超强能力”的数学核心素养，必定是在数学学习过程中获得并逐渐培育起来的，它和数学教育、数学学习的价值与目标在本质上是一致的。南京大学郑毓信教授说：“数学学习的一个主要价值就是有利于人们思维方式的改进，并能使人们逐步学会更清晰、更合理、更深入地思考问题。”[2]为此，他进一步说明：从数学教学或数学教育过程来看，应更加强调“通过数学帮助学生学会思维”，即“将数学思维的学习与具体数学知识内容的学习很好地结合起来”“用思维方法的分析去带动具体知识内容的教学”。[2]可见，思维是数学能力之“核”，思维也是数学素养之“魂”！无论过去、现在，还是将来，数学课堂都应该基于“思维”教，围绕“思维”学，让学生获得良好的思维启迪，能“自觉地用数学的思维方法去观察、分析社会，解决现实问题”（吴正宪语），进而提升学习质量、生活质量乃至人生境界。

二

谈到数学思维，大家关注比较多的，一是数学学习过程中的诸多思维方式，如观察、想象、猜想、验证、分析、比较、归纳、概括、抽象、推理、建模等；二是数学思想方法，如福建师范大学李祎教授就从思维的视角将数学思想方法分为观察与实验、类比与猜想、归纳与演绎、分析与综合、抽象与概括、特殊化与一般化、比较与分类等。在我看来，数学思维方式、方法和数学思想不仅是相通的（方式、方法凝聚成思想，思想以方式、方法具体化），而且是“一体”的（方式、方法中蕴含着思想）。因此，要想“通过数学帮助学生学会思维”，就要让学生在学习中更多地感悟、理解、掌握和运用数学思想，学会用数学的思维方式思考问题。但是，从思维发展的更高要求来看，从学生能“自觉地用数学的思维方法去观察、分析社会，解决现实问题”的目标来看，数学学习又不应停留在这些思维方式、方法的简单使用上，而要突出学习者的主体自觉，增强对更加上位、更加统整、更具“超能”的较高水平的思维品质的培养。

1.整体与结构。

数学是整体的，其主要表现为数学知识的系统性和结构化。任何数学内容都来自于某一系统，从属于某一结构。从结构的角度来把握所学习的数学内容，不仅能凸显内容的实质，建立内容之间的联系，而且有利于学生形成“从结构的角度把握事物本质”的结构化思维。学习数学时一旦有了整体性思维和结构化思维，就会事半功倍。

比如，在一年级，学生大部分时间都在学习加法和减法，从数的分解与组成，到一图两式、一图四式（即看一幅图写出两道加法算式和两道减法算式），再到含有扩线的应用问题和纯文字的应用问题，看起来学了很多，实质上都跟一年级最初认数时学习的“分与合”相连，所有的加减法问题都可以用图1（分支图）表示。一图四式，从“分”的角度想，就是两道减法算式；从“合”的角度想，就是两道加法算式。含有扩线的应用问题，求总数（如图2），就是“合”，问号就表示分支图的总数，而部分数是已知的（可以打√来表示）；求部分数（如图3），就是“分”，问号就在分支图中需求解的部分数上方，其余的都是已知的。至于解答纯文字的加减法实际问题，都可以用分支图来转换，辅以“√”和“？”。这样，整个一年级加减法的学习，不仅有了主线和灵魂，而且建立了直观模型。用这种生动、鲜活、形象的方式来表达数学的整体结构，又会不断培育学生的整体性思维、结构化思维、系统性思维，让学生获得学习数学的重要“法宝”。

图1

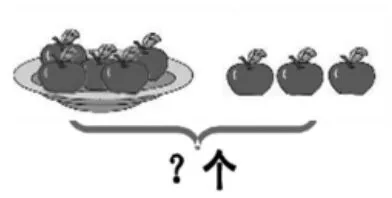
图2

图3

再比如，“可能性”的教学最重要的是把握“可能”“不可能”“一定”这三个数学概念之间的关联。而要把握好它们的关联，必须回到上位概念系统——“确定性事件”（也叫“必然事件”）与“不确定性事件”（也叫“随机事件”“可能事件”）。教材编排大多是从“可能”“不可能”“一定”三个词语的应用出发的，并没有突出上位概念，使得不少教师的教学常常浮于表面。加之在日常生活和语文学习中，“可能”“不可能”“一定”都属于高频词，学生在头脑中很容易把它们的日常意义与数学意义相混淆。解决这一问题的最好办法，就是在教学中逐步完善知识结构（如图4）。这样一来，不仅知识体系一目了然，而且这个结构一直贯穿到初中的概率学习。

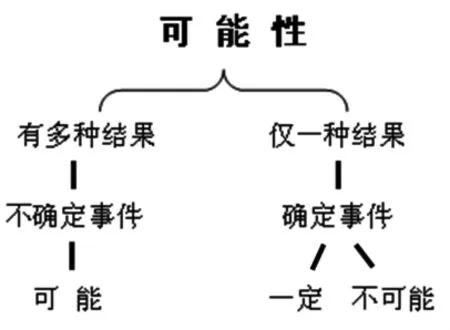
图4

总之，对数学学科而言，知识的整体性与结构化是毋庸置疑的。但是，“化整为零”、螺旋上升式的教材编写体例让知识的整体与结构“散架”了，变得“隐蔽”了，这在一定程度上容易让教师的教和学生的学陷入“只见树木、不见森林”的陷阱，对此，我们要十分警惕。

2.逻辑与理性。

逻辑的严密性是数学学科的重要特点。而严密性的背后，蕴含着极强的逻辑与理性。正如美国数学家柯朗和罗宾所说：“数学，作为人类思维的表达形式，反映了人们积极进取的意志、缜密周详的推理及对完美境界的追求。”数学知识的内涵十分丰富，密切的联系、严密的推理、抽象的概念、恒定的规则等都是数学内容的理性表达，闪烁着数学理性的光芒。

数学学习不能停留在“是什么”，还要明白“为什么”。对“为什么”的追问可以看成是培育学生理性思维的一个重要方面。

比如，在学习了长度单位“千米”之后，从建构系统的角度出发，教师可引导学生整理出已经学过的5个长度单位的关系图（如图5）。有了这样的整理，学生就可以比较轻松地实现长度单位之间的转换。但是，在图5中，存在一个很明显的“疑点”——相邻两个长度单位之间的进率大多是10，唯有“米”和“千米”之间的进率是 1000。为什么完美的“规律”被打破了呢？既不美观，也不符合常规啊？原因就在于在教材中没有将“十米”和“百米”这两个生活中很少用到的长度单位编排进去，如果将这两个长度单位补充到原有结构图中，可得到图6。有了这样的结构图，学生对“米”与“千米”之间的进率是1000就会有更深入的理解，感受到数学原来是如此美好，充满着规律和节奏。

图5

图6

此外，数学知识作为一种抽象的存在，很多时候都超越经验，此时必须借助于理性的思考才能领悟其本质。比如，数学上的点是没有大小的，线是没有粗细的。

除了数学知识本身的逻辑，还有课堂教学的逻辑。比如，对人民币的认识，其教学逻辑顺序是这样的：通过分类比较，发现人民币有元、角、分三个单位；结合日常经验，得出这三个单位之间是有联系的，即1元=10角，1角=10分，1元=100分；因为这种联系，产生了丰富多彩的钱币换算。

当然，数学的逻辑和理性与批判性思维紧密相关。在学习中，应引导学生多问几个“为什么”，多为自己的想法作出解释与说明，多对产生的结论进行质疑和论证。长此以往，理性的哲思必将塑造学生的理性气质。

3.主体与创造。

数学是人类文化的重要组成部分，它和其他文化一样，彰显着人的主体精神与创造性，散发着自身迷人的学科气息。因而，数学课堂上要特别关注学生的主体参与，在探究、反思、感悟、发现中去粗取精、去伪存真、由表及里、化繁为简，让知识慢慢“长”出来，让学习真正发生。

比如，在学习“长方形和正方形的认识”后，面对“在方格图上画一个长方形，再在长方形中画一个最大的正方形”的实践活动，由于学习水平的差异，学生中出现将正方形画到长方形外面（边长大于宽）、将正方形画在长方形内部（边长小于宽）、正方形有两条边分别和长方形的长在同一条直线上等情况属于很自然的事，但是面对这三种情况，教师是直接让学生知道答案（正方形有两条边分别和长方形的长在同一条直线上），还是让学生展示自己画的图，讲述自己的思考并相互评价呢？很显然，我们需要的是后者，也就是让学生先呈现将正方形画到长方形外面的情况，让大家都明白看清题目要求很重要；然后来看没有画在外面的情况，相互讨论和辨析；最终搞明白“长方形中最大的正方形”是怎么回事。在这一“逐步逼近答案”的过程中，学生的收获不只是解决了所给问题，而且还经历了“再创造”的过程，获得了分析、解决问题的思路，体验到独立思考和合作学习的必要性。

强调学生主体性，教学就要指向具有创造色彩的思维精神（即弗赖登塔尔的“再创造”）。将学习过程变成创造过程，学习就不再是机械、被动的接受，而是鲜活、灵动的创新实践，数学学习的世界也会变得更加开放、更加人文，衍生出无限精彩！从这一角度来看，学生学习数学的过程就是建造自己思维世界的过程。

三

如何让学生通过课堂学习获得整体与结构、逻辑与理性、主体与创造等更高水平的思维品质呢？我们提出“用数学的方式学数学”的想法，其实施路径如下：

1.教师在备课时，应充分考虑数学知识内在的整体性、结构性、严谨性、逻辑性等，形成具有鲜明的整体性、结构性、严谨性、逻辑性特色的教学设计，努力让数学课堂与数学的学科特点相呼应。

2.学生在数学学习过程中，能从数学知识内在的整体性、结构性、严谨性、逻辑性出发，并获得与此相关联的学习经验和启示。

比如，学习了毫米、厘米、分米、米这四个长度单位后，可以让学生整理已经学过的四个长度单位，并据此猜想“要是在此基础上人们创造出了第五个长度单位，这个长度单位可能会在什么位置？跟与之相邻的我们已经学过的一个长度单位之间有什么联系”。学生根据已有的长度单位结构图，可能会创造出一个比毫米还小、与毫米的进率也是10的长度单位（即“丝米”），或者创造出一个比米还大、与米的进率也是10的长度单位（即“十米”）。以此类推，“忽米”“微米”“百米”“千米”也会被学生“发明”出来。这样的学习，在一定程度上体现了郑毓信教授所倡导的 “将数学思维的学习与具体数学知识内容的学习很好地结合起来”“用思维方法的分析去带动具体知识内容的教学”的要求，学生在系统中感受整体，在结构中实现建构，在思维中学会思考。

在经历长期的上述数学学习后，在经历一次又一次的观察、想象、猜想、验证、分析、比较、归纳、概括、抽象、推理、建模等思维活动后，在经历一次又一次的体验、感悟、点拨、濡染、强化后，学生的数学思维感觉会变得越来越好。渐渐地，他们就会有意识地将整体思维、结构思维、逻辑思维等应用到新的数学学习活动之中，尝试着进行整体建构、逻辑推断、自主创造。

当学生的思维水平越来越高，自动化程度越来越高时，他们就能将在数学学习中所获得的各种思维能力及整体与结构、逻辑与理性、主体与创造等思维品质，自觉、主动地应用到其他学科的学习及日常生活中。若能这样，我们就可以说，他们的数学素养真正形成了，数学教育的价值也真正实现了。

总的来说，数学核心素养的培育并非一朝一夕所能达成的，而是一个长期的、不断累积进而逐渐从量变到质变的过程。尤其值得注意的是，尽管抽象、逻辑、理性等是数学的重要特征，但是，小学生的数学学习恰恰需要通过直观来表达抽象，用感性去触摸理性，因此，在数学学习的过程中，依然需要有鲜活的情境、有趣的故事、好玩的游戏、形象的图画、生动的演示……多种直观形式的“叠加”，除了能增强学生的直觉感受、活化学习资源、活跃学习气氛、提高学习效果，还能实现多种思维方式的融合。这也正是郑毓信教授所强调的：数学思维显然并非思维的唯一可能形式，各种不同的思维形式，如文学思维、艺术思维、哲学思维、科学思维等，又都有其一定的合理性和局限性，从而，我们就不应唯一地去强调“帮助学生学会数学地思维”，“应当跳出数学，并从更为一般的角度去认识各种数学思想与数学方法的普遍意义。”

如此看来，“为思维而教”应该被赋予更加丰富的时代意义！

[1]编者.编者按[J].人民教育，2015（11）：63.

[2]郑毓信.数学思维与小学数学[M].江苏教育出版社，2008.

（作者单位：江苏海安县城南实验小学）