日本教科书中“圆面积”的编排及启示
——日本小学数学教科书评介之一
◇代 钦
日本教科书中“圆面积”的编排及启示
——日本小学数学教科书评介之一
◇代 钦
一、前言
日本现行中小学学制为“六三三”制,小学六年,初中、高中各三年。日本把小学数学叫作“算数”,意味着小学“算数”还没达到“学”的标准,仅作为知识的掌握及计算技能和作图技能的掌握来处理。《算数》教科书小学一年级1册,二至四年级各2册,五、六年级各1册。从整体上看,和我国小学数学教科书有很多不同之处,有些不同点也许对我国小学数学教育教学有重要的借鉴价值,因此借《小学教学》编辑部约稿的良机,分几个部分来评介《算数》内容。这里在介绍相关知识背景的基础上,仅对《算数》中的“圆面积”内容进行评介。
本文以启林馆出版的从2015年开始使用的《算数》教科书为对象评介“圆面积”内容。日本教育当局进行教育改革时格外谨慎,教育改革进程十分缓慢,正如日本著名教育家佐藤学所说的“静悄悄的革命”那样,十年左右进行一次改革,每次改革都要修订 “学习指导要领”(相当于我国的课程标准,以下简称“课标”),根据“课标”编写教科书,“课标”颁布后不能立即实施,新教科书出版后也不能立即投入使用,而是经过数学教育研究者、一线教师和学生家长等个人和团体四年的学习领会之后才能够实施和使用。这样人们对“课标”和教科书就会有一个系统、全面的认识。日本中小学的新教科书并不是同一年开始使用的,而是按照小学、初中和高中逐年开始使用,其主要原因是为了保证小学、初中和高中之间内容的有效衔接。这与我国的情形截然不同,我国的做法是新课标和新教科书出台后立即进行新一轮的教学改革,广大中小学教师措手不及,主动或被动地参加各种培训,学习课程改革的理念。相比之下,日本没有大张旗鼓的教师培训,他们的培训都是在学校的自我研修过程中完成的,其中教师的主动性和积极性起到关键作用。
为了使国内小学数学教育工作者更好地了解日本《算数》,这里先介绍六年级《算数》内容的结构。
1.对称图形:①轴对称;②中心对称;③多边形与圆;④用镜子观察对称。快乐地学习“算数”。
2.字母与式:①使用字母的式;②式的读法。
3.分数×分数:①分数的乘法计算;②分数乘法的应用。
4.分数÷分数:①用分数除分数;②分数除法的应用。
5.圆面积。
6.比及其应用:①比与比值;②相等的比;③应用比的问题。是什么样的计算呢?分情形进行调查;暑假的“算数”自由研究。
7.图形的放大与缩小:①放大图与缩小图;②放大图与缩小图的作法;③缩小图的应用。“算数”实验室。
9.比例与反比例:①比例;②比例的应用;③反比例。
10.立体体积。
11.形状与大小的估测。
13.按情形的顺序整理资料:①情形的数的调查;②考虑各种情形。估算方法的应用;飞向未来的翅膀;读懂的“算数”;分割的应用。
14.量的单位。
●六年级的总结。
○“算数”毕业研究。
每一章节的目录中,均标示了之前学过的相关知识的链接,如“1.对称图形”的前面标示了“五年级的合同图形、圆与正多边形”。“”标示的是问题解决的内容,由问题的提出、自主学习、共同讨论、确认、提出进一步思考的问题等五个步骤构成。“”标示的是通过调查、动手操作以后得出若干结果的探索题,具有开放题的性质。“●”标示的是一学年学习内容的总结,如“六年级的总结”共有15页。“○”标示的是“算数”毕业研究,相当于毕业“创作”,其内容有以下历史名题:高斯计算方法、帕斯卡三角形的秘密、一笔画问题的秘密、莫比乌斯带的不可思议、斐波那契数和直角三角形秘密等的学习探究。
二、圆面积公式的探究
“圆面积”在上一版本《算数》中安排在五年级下学期,在现行版本中安排在六年级上学期,内容的量和难度差别不大。“圆面积”的学习由实验、自主探究、合作讨论、一题多解、历史考察等步骤组成,旨在使学生有效地习得知识、掌握数学思想方法、领会人类探究圆周率的历史。具体展开过程如下:
问题1:怎么求圆的面积呢?求半径为10cm的圆的面积时,先观察下面两幅图中的正方形和圆的关系,得出了什么结论?(如图1、图2)
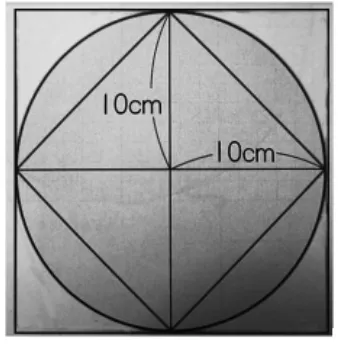
图1

图2
观察之后发现:
边长为10cm的2个正方形的面积<半径为10cm的圆的面积<边长为10cm的4个正方形的面积。
问题2:半径为10cm的圆的面积是什么样的?(注:这里使用了“面积是什么样的”而不是“面积等于多少”)
教科书中的方格纸上有半径为10cm的圆,如图3,假定每一方格的边长为1cm。(注:日本小学《算数》中与圆形有关的内容多采用方格纸)
如何考察呢?让学生数数该圆有多少个完整的方格(蓝色)和不完整的方格(红色),(注:按原版教科书中彩图说的蓝色和红色)将2个不完整的方格当作1个完整的方格,这样把全部方格相加就是圆面积。但是这样做工作量过大,因此将该圆进行四等分,如图4,让学生考察其中一部分,数数有多少个方格。1个蓝色方格面积为1cm2,1个红色方格面积为0.5cm2。结果得出个圆的面积为。从而整个圆面积大约是 S= 310cm2。

图3

图4
完成上述步骤后发现求圆的面积并非易事,于是提出:能否找到一个简单的方法——圆面积公式?
第一种情形:将圆逐级等分,每一个小部分看成一个小三角形,并化圆为平行四边形,再化为长方形,求出长方形的面积,再将长方形的面积还原为圆的面积。如图5,将圆8等分、16等分、32等分、64等分,并用小扇形拼成图,越来越接近长方形。假定:将圆64等分后转化成长方形,即长方形的面积等于圆的面积。
长方形的面积=宽×长=半径×圆周长的一半
圆面积=半径×圆周长÷2
=半径×直径×π÷2
=半径×直径÷2×π
=半径×半径×π
通过以上探究最后得到圆面积的公式:

推导出公式后让学生计算半径为10cm的圆的面积(π取3.14),并与观察到(估算出来)的方格纸上的圆面积的结果(S=310cm2)进行比较。

图5
进一步探究:经过求解以下几何图形中阴影部分面积的练习(如图6),又回到圆面积公式的推导过程的讨论。求解阴影部分面积的练习也是探究式的,其实际教学进程是循序渐进的,节奏并不像我国小学数学课堂教学那样快速、紧张,求解这些阴影部分的面积需要2节课以上时间。
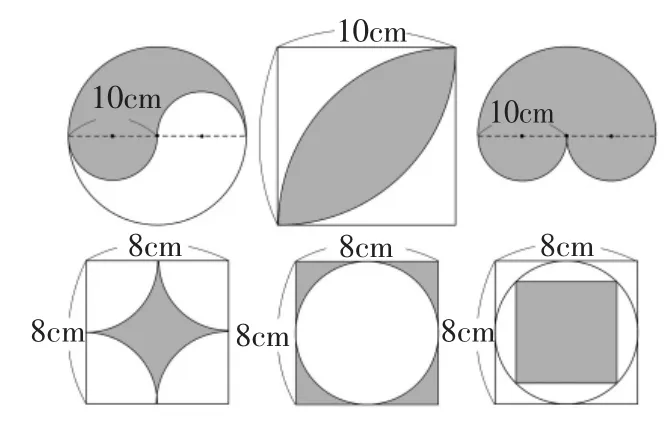
图6
第二种情形:首先,让学生观察厚度均匀的带子卷好形成的圆和用带子堆积起来形成的三角形之间的关系(如图7),这里带子的每一圈为所堆积起来的三角形的每一层。在此启发下,将圆逐级等分,每一个小部分看成一个小三角形,并用小三角形制作大长方形,再利用等底等高的三角形面积相等的性质构造大三角形,其底边长等于圆周长,如图8,将大三角形的面积还原为圆的面积:

图7
大三角形的面积=底×高÷2
圆面积=圆周长×半径÷2
=直径×π×半径÷2
=半径×2×π×半径÷2
=半径×半径×π
第三种情形:将圆16等分,每一个小部分看成一个小三角形,并用小三角形制作大三角形,再将大三角形的面积还原为圆的面积。如图9,16个小三角形正好堆积成一个大三角形,大三角形的底边等于圆周长的,高等于半径的4倍。
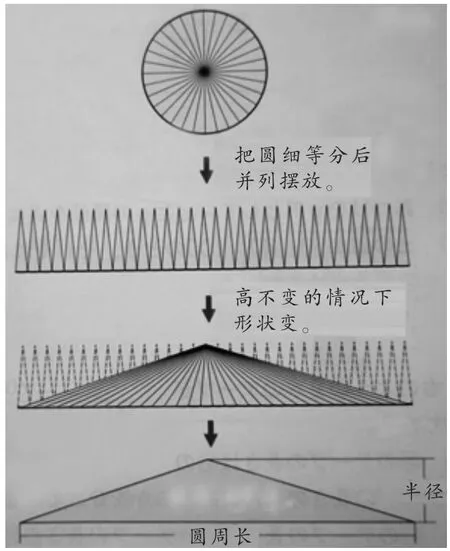
图8

图9
大三角形的面积=底×高÷2;
圆面积=圆周长÷4×半径×4÷2
=直径×π×半径÷2
=半径×2×π×半径÷2
=半径×半径×π
上述圆面积的一系列探究告一段落后,安排了阅读材料——“圆周率的历史”:
圆周率的历史
用小数表示圆周率就是3.14159265358979…,它是一直延续的永远不会终结的数,迄今为止,用超级计算机计算到1兆2411亿位。但是在古代计算圆周率是一件非常困难的事情。
(1)在遥远的古代,取圆周率为3。
(5)大约300年前,日本的关孝和把圆周率计算到3.14159265359。
试将(2)~(4)中的分数转换为小数。
(注:这里省略了相关图片)
三、启示与借鉴
启示与借鉴,是指每一个人根据自己的判断调整自己原有思维和行动的行为。这里的“启示与借鉴”是我个人的一些想法,仅供参考。我们慢慢地浏览日本小学《算数》中“圆面积”的探究过程时,很自然地联想到其编写者们的研究深入、设计精巧和见解独特。“圆面积”不能代表日本小学《算数》的全部内容,但是它从一个侧面反映了日本《算数》的课程理念、设计意图和特点。其他内容的设计特点和形式与“圆面积”基本相同。我们在“圆面积”中至少看到以下几个方面:
首先,以问题为导向的内容设计有利于学生数学思维的发展。“圆面积”的设计几乎每一步均以问题为导向,引入新内容时提出问题,中间和最后结果也是以括号形式呈现,让学生自己寻找在括号中填写的结果,这就相当于让学生回答相应的问题。
其次,在以问题为导向的基础上,以探究形式安排内容,以保证学习的有效性。如引入“圆面积”时,并不是开门见山地直接推导圆面积公式,而是观察同一圆的外切正方形、内接正方形与该圆的面积之间的大小关系,体现了数学中的逼近思想方法。在小学阶段能够如此巧妙地设计内容是难能可贵的。找到圆和正方形面积的不等关系,用方格纸方法观察半径为10cm的圆的面积,得出近似结果。由于这种求圆面积的方法过于笨拙、烦琐,于是提出了寻找更简单的一般方法——圆面积公式的要求。用“以直代曲”的方法将圆逐级等分为小扇形,将小扇形看作小三角形,构造长方形,再推导出圆面积公式。在这之后并没有停止探究,而是深入浅出地进入“圆面积”的第二种情形和第三种情形的探究。这些探究过程,使学生潜移默化地领会了数学中的观察法、逼近思想方法、直观与抽象相结合的思想方法、一题多解的思想方法,从而可以有效提高学生提出问题、分析问题和解决问题的能力。
再次,“圆面积”内容设计中,注重动手操作与数学思维的有机结合。要求学生自己作图、观察并记录、动手实验,在此基础上,使学生通过计算、推导得出一般结论。即使阅读材料,也是让学生边阅读边动手计算,将圆周率的分数表示改变为小数表示,这样也能很好地培养学生一丝不苟的学习习惯和学习自信心。
最后,“圆面积”设置了阅读材料“圆周率的历史”,仅用一页图文并茂地展现了圆周率几千年的发展史,古埃及人、古希腊的阿基米德、中国的祖冲之、日本的关孝和的相应成果,充分体现了不同文化和民族对圆周率的探索作出了各自的贡献。在数学教科书中涉及文化历史方面的阅读材料时,在充分展现本国重要成就的同时,也要合理安排他国的不同文化作出的相应贡献的内容,这样能够克服以自我为中心的狭隘的观点,培养学生更加开阔的多元文化观。
[1]清水静海,船越俊介,等.快乐的算数6[M].大阪:株式会社新兴出版社启林馆,2015.
[2]日本文部科学省.小学课程标准[S].东京:东京书籍株式会社,2008.
[3]冈本和夫,根本博,等.面向未来的数学[M].大阪:株式会社新兴出版社启林馆,2015.
(作者单位:内蒙古师范大学科学技术史研究院)

