初中数学动点路径长的问题解决策略

蒋亨强（长乐华侨中学，福建长乐350299）

初中数学动点路径长的问题解决策略

蒋亨强
（长乐华侨中学，福建长乐350299）

路径长问题的通常没有给出具体的动点运动轨迹，比较抽象，是学生难以把握的问题之一。问题的解决策略是将动态问题转化为静态问题，寻找问题中的不变量，把抽象问题具体化，而初中阶段动点的运动轨迹一般只限于直线运动或圆弧运动，解决路径长问题关键在于确定动点运动的轨迹。

轨迹；运动；路径长；策略

路径长问题是近几年中考的热点问题，它设计新颖，内涵丰富，既考查学生的基本画图能力，又考查学生逻辑推理能力。它的难点在于题目中没有给出具体的动点运动轨迹，而且比较抽象，需要学生思考探究，很多学生对这类问题常常感到无从下手，产生畏难情绪。为了解决这个问题，教师可以引导学生将动态问题转化为静态问题，寻找路径长问题中不变的量，把抽象问题具体化。现结合例题探讨动点路径是线段与圆弧这两类问题轨迹的解题策略。

一、追根溯源，探究问题中不变的量

教学过程中教师们常常发现学生在审题、析题方面不能抓住重点，遇到疑难问题，不懂得寻求解题的突破口，过度依赖教师的讲解，不能独立思考，学习处于被动状态。新课程理念倡导以学生为主体，让学生积极、主动地参与课堂的探究活动，学生通过探究获得的解题经验往往比较直观，而且印象深刻，因此，教师传授新知识、新方法时，要让学生有充足的时间探究题目中隐含的条件，寻找解题的关键点，把复杂问题简单化。学生在探究的过程得出解题经验，既获得成功的体验，又提高自身的综合解题能力。

1.动点到定直线距离保持不变，其轨迹是线段

人教版七年级下册数学教科书采用这个例题来讲解无理数π如何在数轴上表示。如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点由原点O到达点O′，点O′的数值是___。这是初中阶段教科书第一次讲解动点的轨迹问题，从图中可以看出O O′的长是这个圆的周长π，所以点O′在数轴上对应的数是π。教师再让学生思考圆形车轮让乘坐者感觉舒适平稳的原因，学生探究后得出结论：圆心到水平面的距离相等。透过现象看本质，这就为探究动点路径长问题提供了解题的思路。

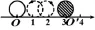
例如：如图所示，一个扇形的半径为3cm，圆心角∠AOB=60°，让弧AB在水平面上滚动，探究圆心O经过的路径长是多少cm？

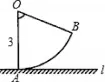
该题如果把扇形所在的圆完整地画出来，参照上题可得，整个圆滚动中圆心O到定直线l的距离都等于3cm。这就是该题不变的量，也是解题的突破口。学生通过讨论，探究得出因为弧AB在水平面上滚动过程中，圆O始终保持与定直线l相切，又因为动点O到弧AB上任意点的距离都等于定长3cm，所以圆心O经过的路径是一条平行水平面的线段。长度就是弧AB的长=nπr/180=60×π×3/180=πcm。学生通过回顾典型特例，采用类比的方法探究解题的思路，有助于抓住重点，突破难点，有利于促进学生对解题方法的理解，促进学生更深入地学习，熟练掌握这一类型题目的解题思路。

2.动点到定点距离保持不变，其轨迹是圆弧

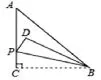
例如：如图所示，在Rt△ABC纸片中，∠C=90°，AC= BC=4，点P在线段AC上运动，将纸片沿PB折叠，得到点C的对应点D（P在C点时，点C的对应点是本身），则折叠过程对应点D的路径长是多少？

根据圆的定义，当动点到定点距离保持不变时，定点就是圆心，定长就是半径，动点的路径就是圆弧。解题时先让学生探究：动点D到哪一个定点的距离保持不变？学生通过分析可得：当动点P在起始点C时，动点D在C点；当动点P在结束点A时，PB与AB重合，对应的动点D是C点关于线段AB的对称点，根据折叠对应线段相等可得BD=BC=4，所以动点D到定点B的距离保持不变，都等于4，这就是该题不变的量，所以动点D的轨迹是圆弧，点D的路径长是圆弧CD的长。如图，∵∠C=90°，AC=BC=4，∴△ABC是等腰直角三角形，∴∠CBA=∠A= 45°，由折叠对应角相等可得∠CBA=∠DBA=45°，∴∠CBD=90°。∴弧CD长=nπr/180=90×π×4/180=2π，即折叠过程对应点D的路径长是2π。学生通过探究活动，确定动点路径后，再运用弧长公式计算其长度，可从中体会数学的转化思想，发现解题的突破口，找到解题的最佳方案，提高解题析题的能力。

二、数形结合，三点定位找轨迹

当路径长问题中不变的量不明确时，需要运用“两点确定一条直线”的直线公理。采用数形结合法，找三个特殊点，如运动起始点、运动中任意一点、运动结束点。然后确定这三个动点的对应点，因为动点的轨迹只限于直线或圆弧，可做如下猜想：若这三个对应点是在同一直线上，其路径即为线段；若这三个对应点不在同一直线上，其路径即为圆弧；把这三点用线段或圆弧连接起来，动点的运动路径就具体化了，这种解题思路体现了从特殊到一般的化归思想。数学方法理论的创导者波利亚曾说：“数学首先是猜想，然后才是证实”，学生为了证实自己猜想，在观察、讨论、交流、验证的过程中，理清关系，说明理由，探索解题策略，形成系统化的认识。

例如：如图1，已知AB=10，点C、D在线段AB上，且AC=DB=2，P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连结EF，设EF的中点为G；当点P从点C运动到点D时，求点G移动路径的长是多少？

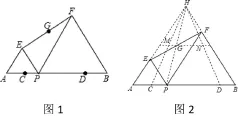
该题的不变量不容易找到，应先从特殊三点入手，画图后观察这三点的对应点是否在同一条直线上。解题一般分以下4个步骤：

①画图：画动点P在起始点C时，对应的动点M，点P为任一点时，对应的动点G，动点P在运动结束点D时，对应的动点N，连结点M、G、N，发现这三点在同一直线上。

②猜想：动点G的路径长为线段MN。

③说理：如图2。分别延长AE、BF交于点H。∵∠A=∠FPB=60°，∴AH∥PF，∵∠B=∠EPA=60°，∴BH∥PE，∴四边形EPFH是平行四边形，∴EF与HP互相平分。∵G是EF的中点，∴G是PH中点，即在P的运动过程中，G始终为线段PH的中点，∵点M是线段HC中点，点N是线段HD中点，所以G的运动轨迹为△HCD的中位线MN。

④计算：CD=AB-AC-DB=10-2-2=6，∴MN=3，即点G移动路径的长为3。

该题通过引导学生画出动点三个特殊位置的对应点，先猜想，后根据等边三角形性质定理、平行四边形判定定理和性质定理、三角形中位线定理，推理得出动点G始终为线段PH的中点，所以动点G的运动轨迹为△HCD的中位线MN。挖掘出该题中不变的量就是动点G到定直线AB的距离。由此可见，在解题中不仅需要结合题目的已知条件，仔细分析，还需从特殊点入手，从特殊到一般，由浅入深，仔细推敲，挖掘题目中隐含的不变量，找出动点的运动轨迹，既要让学生明白问题是如何解决的，更要让学生明白为什么要用这种方法解决，做到知其然，更要知其所以然。对学有余力的同学，教师还可布置分层作业，如该题能否引入平面直角坐标系，用两点待定系数法先确定一条直线的解析式，再把第三点坐标代入验证三点是否共线，解题后要不断反思，总结经验，做到举一反三，融会贯通。

求动点路径长问题一般先寻找题目中不变的量，当动点到定直线距离保持不变时，其轨迹是线段；当动点到定点距离保持不变时，其轨迹是圆弧；当不变的量不明确时，采用三点定位确定动点的轨迹，解题一般分4个步骤：①画图，画出动点在三个特殊位置的对应点。②猜想，路径是线段或圆弧。③说理，利用定义或定理论证得出的结论。④计算，根据已知条件，利用公式计算路径长。路径长问题转化为求线段长或弧长问题，实现了动点问题静态化，帮助学生克服畏难的心理。新课程改革提倡让学生掌握基本技能、基本方法的同时，要掌握解题的方法和技巧，总结出这类题型的解题策略，形成数学的思想方法。这不仅有助于提高学生的学习效率，而且对培养学生的探究意识和创新能力，都具有重要的意义。

［1］中华人民共和国教育部.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］李爱琴.对运动路径长问题的思路探究［J］.初中数学教与学，2012（13）.

［3］邓文忠.例析中考动点路径长问题［J］.数理化学习，2014（1）.

（责任编辑：王钦敏）