变论域模糊PID在微碳汇测量系统中的仿真研究

于越，宋文龙，王琢

(东北林业大学 机电工程学院，哈尔滨 150040)

变论域模糊PID在微碳汇测量系统中的仿真研究

于越，宋文龙*，王琢

(东北林业大学 机电工程学院，哈尔滨 150040)

在微碳汇研究中，分析植物在不同温度条件下的碳转换能力是必要的。针对微碳汇测量系统中温度变化具有的非线性、时变性、滞后性等问题，提出一种改进型变论域模糊PID控制方法。该方法采用分段函数作为伸缩因子，实现论域的等效伸缩；分段函数伸缩因子在保证控制精度的同时减少运算步骤，从而减小系统的滞后性，提高系统响应的实时性。采用MATLAB/Simulink分别对PID控制器、模糊PID控制器、变论域模糊PID控制器进行建模仿真，仿真结果表明：采用改进变论域模糊PID方法控制系统温度，调节时间短，最大超调量小，跟踪能力好，能为研究植物碳汇能力与温度的关系提供良好基础。

微碳汇；变论域；模糊PID控制；伸缩因子

0 引言

微碳汇测量指测量单株植物对环境中CO2的固定能力或固定量，微碳汇的研究重点是分析环境因子(温湿度、气体浓度和光照强度等)与植物固碳量的关系。在采用箱式法[1-2]进行微碳汇研究时，需要对微碳汇测量系统中的环境因子做到精确的控制。温度是影响植物碳汇的重要因素之一，实现系统内部温度的精确控制利于找到植物碳汇能力与温度的关系。

微碳汇测量系统内部温度系统具有非线性、滞后性、耦合性，传统PID控制并不适用。模糊控制适用于非线性系统的控制，但存在静差，且相当于PD控制器，无法消除静差，控制精度低[3-5]。模糊PID控制引入积分环节，可消除静差，提高控制精度，但误差较小时PID参数不易调准，且控制规则数目有限，导致控制精度有限[6-8]。李洪兴[9-11]教授首次将变论域思想引入到模糊控制中，随后又给出两种伸缩因子的数学模型，并通过四级倒立摆控制仿真实验证明了变论域模糊控制具有调整时间短、超调量小、稳态精度高、鲁棒性强等特点，十分适用于处理非线性系统。

研究中采用改进型变论域模糊PID控制方法，实现对微碳汇测量系统的温度控制，提出一种分段函数型伸缩因子，实现对输入模糊论域的在线调整，在保证控制精度的同时降低运算复杂度，提高系统实时性和响应速度，具有比PID控制模糊PID控制更好的自适应能力、跟踪能力和动态响应特性。

1 微碳汇测量系统模型

微碳汇测量系统结构如图1所示。整个系统分为培养箱和工作箱，由隔板1隔开。培养箱主要用于培养和观察植物，采用亚克力板搭建；工作箱主要放置加湿器、制冷系统等，由不锈钢薄板搭建。

图1 系统结构图Fig.1 Incubator structure diagram

其中热风机实现系统升温，分别安置压缩机、冷凝器、蒸发器形成空调制冷系统实现系统降温，空气温度变送器采用MQ3485，测量分辨率可达±0.1℃。

微碳汇测量系统温度变化过程复杂，受空气湿度、植物蒸腾作用、蒸发作用、通风系统、热交换等多种因素影响，不易建立精确的数学模型。文献[12]证明类似温室的温度控制系统的理想数学模型可简化为一阶滞后模型，根据实际测量数据并采用切线法[13]可得微碳汇植物培养箱温控系统的等效数学模型为：

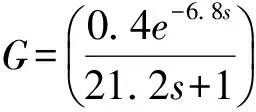
(1)

2 变论域模糊PID控制器设计

2.1 变论域模糊PID温控系统结构

根据变论域原理可知，如果利用伸缩因子直接改变模糊论域的大小，相当于压缩或扩张各个模糊子集的隶属度函数，需要逐点计算，计算量过大，难以实现。现采用一种等效办法，即当输入量接近零点时，输入伸缩因子增大量化因子，从而增大输入量，相当于压缩输入模糊论域，且输入量越接近零点，输入伸缩因子增大量化因子的程度越大；清晰化后，为保证输出量符合实际，输出伸缩因子应根据量化因子增加的程度相应减小比例因子，相当于压缩输出模糊论域。需要注意的是，输入输出模糊论域的压缩与扩张是同步的。

变论域模糊PID温控系统结构如图2所示。

图2 变论域模糊PID温控系统结构图Fig.2 Variable universe fuzzy PID temperature control system structure

其中ke和kec为量化因子，lp、li、ld为比例因子，系统通过误差e和误差变化率ec计算输入输出伸缩因子，结合量化因子和比例因子共同实现输入输出模糊论域的等效伸缩，其中量化因子与输入伸缩因子是相除关系，比例因子与输出伸缩因子是相乘关系。ΔKp、ΔKi、ΔKd为模糊控制器的输出量，在线调节PID控制器参数Kp、Ki、Kd。

2.2 伸缩因子的设计

变论域模糊PID控制器设计的关键在于伸缩因子的选择。目前，基于函数型和基于模糊推理型的伸缩因子较常用[14]。模糊推理型伸缩因子计算量大，实时性差，故选用函数型伸缩因子。由于在输入较小时，伸缩因子作用才比较明显，故考虑对论域有条件的伸缩，在传统比例型伸缩因子的基础上，提出一种分段比例函数作为输入伸缩因子，在保证控制精度不被影响的同时可减小计算量。若温度误差e与误差变化率ec的基本论域分别为：Xe=[-xemax，xemax]，Xec=[-xecmax，xecmax]，则输入伸缩因子可表示为：

(2)

(3)

其中θi为阈值，i=1,2。仅当输入小于θi时，才通过伸缩因子改变量化因子等效实现对输入模糊论域的伸缩，避免了在整个论域上都进行论域伸缩所带来的不必要的计算。θi的大小决定控制精度和运算量。对于参数λi、εi，前者值越大，后者值越小，控制器对输入的变化越敏感，越有利于减小死区的影响和提高控制精度。经多次试验，选取λ1,2=0.7、ε1=10-5、ε2=10-6。

由于输出伸缩因子直接影响到PID控制器参数自整定，为保证控制精度，不设置阈值。输出伸缩因子可选为：

(4)

2.3 模糊PID控制器的设计

模糊控制器的结构为两输入三输出。输入是温度误差e和误差变化率ec，输出为PID参数校正量ΔKp、ΔKi、ΔKd，温度误差e和误差变化率ec的基本论域分别选为[-10，10]、[-1，1]，输出变量ΔKp、ΔKi、ΔKd的基本论域选为[-1.5，1.5]、[-0.015，0.015]、[-3，3]。输入输出变量的模糊论域均选为[-3，+3]，选7个模糊子集{NB，NM，NS，ZE，PS，PM，PB}划分输入输出模糊论域，对于NB和PB采用高斯隶属度函数覆盖，其他均采用三角形隶属度函数覆盖。

量化因子和比例因子可表示为：

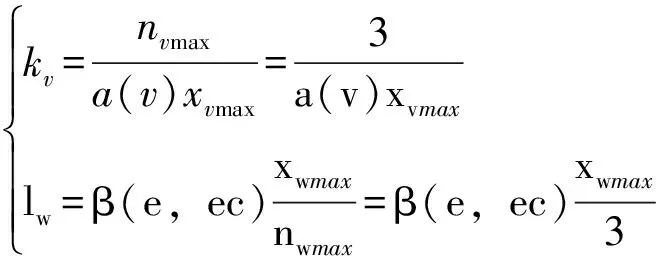
(5)

v代表e或ec，w代表p、i或d，nmax为模糊论域右边界值。

根据经验可得PID参数整定原则如下[14-18]：

e较大时，为使响应速度快，增大Kp；为避免超调，适当增大Kd；为减小积分饱和，减小Ki。

e中等时，为降低超调，减小Kp，为增强系统稳定性，增加Ki，为保证响应速度，Kd取值适中。

e较小时，为保证系统稳定性，减小Kp，为提高系统稳态精度，适当增大Ki，为避免振荡，ec较大时，减小Kd，ec较小时，增大Kd。

根据上述经验得出ΔKp、ΔKi、ΔKd的模糊控制规则见表1。其中E与EC分别为温度误差e和误差变化率ec对应的模糊语言变量。

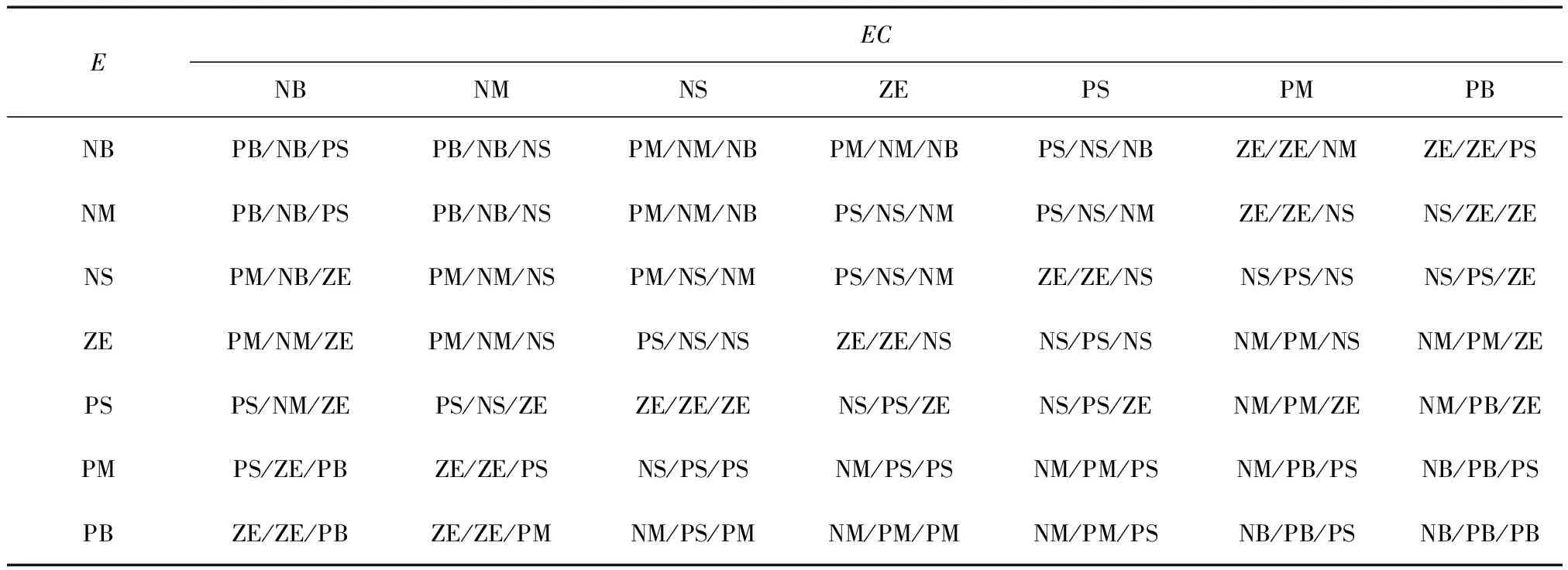
表1 模糊控制规则表

利用重心法[19]对模糊量清晰化可得PID参数整定量ΔKp、ΔKi、ΔKd，则PID参数在线校正公式为：

Kw=Kw0+ΔKw。

(6)

其中Kw0为PID参数初始值，可通过Z-N经验公式法、临界比例度法等进行整定[20]。

3 仿真分析

利用MATLAB中的Simulink软件包分别对微碳汇测量系统建立PID、模糊PID、变论域模糊PID温度控制仿真模型，其中变论域模糊PID仿真模型如图3所示。

采用临界比例度法并通过优化调整，整定常规PID控制器参数为Kp=4.58，Ki=0.375，Kd=20.15；加入模糊控制环节后，模糊PID控制器初始参数设定为Kp0=5.68，Ki0=0.305，Kd0=17.15；加入伸缩因子后，变论域模糊PID控制器初始参数设定为Kp0=5.88，Ki0=0.305，Kd0=15.15。

图3 变论域模糊PID Simulink仿真模型Fig.3 Variable universe fuzzy PID Simulink simulation model

3.1 动态性能对比

假设系统内部初始温度0℃，目标温度25℃，输入阶跃信号幅值为25，仿真时间200s，采样时间0.1s，则常规PID、模糊PID、变论域模糊PID的阶跃响应曲线如图4所示。

图4 阶跃响应曲线Fig.4 Step response curve

3种控制方法的动态响应性能比较见表2。

由表2可知，模糊PID与变论域模糊PID响应曲线的上升时间、超调量、调节时间均明显优于常规PID控制；变论域模糊PID控制相比于模糊PID控制有更好的动态响应性能，整体控制性能更好。

表2 动态响应性能对比

3.2 跟踪及调节控制能力对比

假设系统内部初始温度为0℃，目标温度20℃，200 s时设定目标温度为40℃，400 s时设定目标温度为10℃，输入分段阶跃函数如公式(7)所示，3种控制方法的响应曲线如图5所示。

(7)

由仿真结果可以看出，随着调节量的增大，PID控制器的超调量、调节时间明显增加，模糊PID控制器的超调量、调节时间有所增加，变论域模糊PID控制器时域响应特性增加并不明显，其在较大调节范围内，能快速跟随给定目标温度，调节跟随能力较好。

图5 分段阶跃信号响应曲线Fig.5 Segmentation step response curve

4 结论

针对微碳汇测量系统温度难以精确控制的问题，采用改进变论域模糊PID控制方法，提出一种基于比例型伸缩因子的分段函数伸缩因子，在保证控制精度的前提下，可减少系统计算量，提高系统实时性。利用MATLAB分别对PID、模糊PID、变论域模糊PID建立仿真模型，对3种方法的动态性能、跟踪及调节能力进行对比。结果表明：改进型变论域模糊PID控制方法在超调量、上升时间、调节时间、跟踪及调节能力方面均优于PID控制器和模糊PID控制器，满足温度控制要求，适用于微碳汇研究。

[1]李红琴，李英年，张法伟，等.基于静态箱式法和生物量评估海北金露梅灌丛草甸碳收支[J].生态学报，2014，34(4)：925-932.

[2]蒙光伟.森林碳汇计测方法及其发展方向[J].内蒙古林业调查设计，2012，35(4)：925-932.

[3]郝少杰，方康玲.基于模糊PID参数自整定的温度控制系统的研究[J].现代电子技术，2011，34(7)：196-198.

[4]Nair A P，Selvaganesan N，Lalithambika V R.Lyapunov Based PD/PID in Model Reference Adaptive Control for Satellite Launch Vehicle Systems[J].Aerospace Science and Technology，2016，51：70-77.

[5]Shirkhani N，Khanesar M A，Teshnehlab M.Indirect Model Reference Fuzzy Control of SISO Fractional Order Nonlinear Chaotic Systems[J].Procedia Computer Science，2016，102：309-316.

[6]Chen S H，He H M，Li X F，et al.Application of Fuzzy PID Controller with Self-Adaptive Algorithm and Non-uniform Grid Scheduling to WFGD[J].IFAC Proceedings Volumes，2009，42(9)：20-25.

[7]Rojas I，Pomares H，Gonzalez J，et al.Adaptive Fuzzy Controller：Application to the Control of the Temperature of a Dynamic Room in Real Time[J].Fuzzy Sets and Systems，2006，157(16)：2241-2258.

[8]潘永平，王钦若.变论域自适应模糊PID控制器设计[J].电气自动化，2007，29(3)：9-12.

[9]李洪兴.从模糊控制的数学本质看模糊逻辑的成功──关于“关于模糊逻辑似是而非的争论”的似是而非的介入[J].模糊系统与数学，1995，9(4)：1-14.

[10]李洪兴.变论域自适应模糊控制器[J].中国科学E辑：技术科学，1999，29(1)：32-42.

[11]李洪兴，苗志宏，王加银等.四级倒立摆的变论域自适应模糊控制[J].中国科学E辑：技术科学，2002，32(1)：65-75.

[12]简锋.基于变论域模糊控制的温室大棚温度控制[D].沈阳：沈阳工业大学，2013.

[13]石辛民，郝整清.模糊控制及其MATLAB仿真[M].北京：电子工业出版社，2009.

[14]蒋妍妍，李洪林.基于变论域模糊PID的分解炉温度控制研究[J].测控技术，2014，33(10)：72-75.

[15]Jiang H，Wang X，Zheng Y H，et al.Multiple Models Fuzzy PID Controller Design in Air-Condition Temperature Control System[J].Advanced Materials Research，2013，860-863：1616-1619.

[16]Ang L Y，Jafar F A.Simulation Analysis of Non-Linear Fuzzy PID Temperature Controller[J].Applied Mechanics & Materials，2013，465-466：677-681.

[17]Li P Q，He J，Fan C H，et al.The Design of Temperature and Humidity Control System of Fresh-Keeping Storage Based on Fuzzy PID Inference Algorithm[J].Advanced Materials Research，2013，811：569-574.

[18]王新政，韩玉杰，张海玉.禽舍温度模糊自适应PID控制与仿真研究[J].森林工程，2012，28(2)：50-53.

[19]韩宇光，曹军，朱良宽.刨花板热压控制系统模糊自适应PID控制[J].森林工程，2011，27(4)：30-33.

[20]杨智，朱海锋，黄以华.PID控制器设计与参数整定方法综述[J].化工自动化及仪表，2005，32(5)：1-7.

Simulation of Variable Universe Fuzzy PID in the Micro Carbon Sink Measurement System

Yu Yue，Song Wenlong*，Wang Zhuo

(College of Mechanical and Electrical，University of Northeast Forestry，Harbin 150040)

In the study of micro carbon sink，it is necessary to analyze the carbon conversion ability of plant under different temperature.For the problems such as nonlinear，time-varying and hysteresis of temperature in micro carbon sink measurement system，an improved variable universe fuzzy PID control method was proposed.Piecewise function was used as contraction-expansion factor to realize the equivalent contraction and expansion of universe.The contraction-expansion factor ensured control accuracy while reducing the computational steps so as to reduce the lag of the system and improve the real-time performance of system response.The PID controller，fuzzy PID controller，improved variable universe fuzzy PID controller were simulated and analyzed by MATLAB/Simulink.The simulation results showed that with the improved variable universe fuzzy PID temperature control system，the adjust time is short，the maximum overshoot is small and the tracking ability is good，which can provide a good basis for studying the relationship between plant carbon sink capacity and temperature.

Micro carbon sink；variable universe；fuzzy PID control；contraction-expansion factor

2017-01-18

国家自然科学基金项目(31470714)

于越，硕士研究生。研究方向：模式识别与智能系统。

*通信作者：宋文龙，教授，博士生导师。研究方向：林业工程自动化、控制工程、智能系统。E-mail：swllws096@163.com

于越，宋文龙，王琢.变论域模糊PID在微碳汇测量系统中的仿真研究[J].森林工程，2017，33(4)：44-48.

S 223；TP 273+.4

A

1001-005X(2017)04-0044-05