汽车动力总成悬置系统隔振特性仿真优化

樊攀，包汉伟

(1.宝鸡文理学院 计算机学院，陕西 宝鸡 721016；2.山东新华医疗器械股份有限公司，山东 淄博 255000)

汽车动力总成悬置系统隔振特性仿真优化

樊攀1，包汉伟2

(1.宝鸡文理学院 计算机学院，陕西 宝鸡 721016；2.山东新华医疗器械股份有限公司，山东 淄博 255000)

为解决汽车动力总成悬置系统隔振问题，建立动力总成悬置系统6自由度分析模型，对影响悬置系统隔振效果的关键参数进行分析。根据悬置系统固有特性计算理论，利用ADAMS软件对某动力总成悬置仿真模型进行固有特性分析，得到系统固有频率和能量解耦率；然后运用MATLAB中的优化函数以系统能量解耦率为目标，以悬置元件的主轴刚度为优化变量对悬置系统进行优化。通过优化设计，改进后悬置系统隔振率有了明显上升，并且提高了悬置系统的减震性能。调整悬置元件各主轴刚度，可以降低动力总成悬置系统的振动耦合，提高系统的解耦率，实现固有频率的合理配置。

动力总成；悬置系统；隔振；能量解耦；

0 引言

发动机运转时，曲轴连杆机构高速运动会产生往复惯性力激励，输出到传动系统的转矩也具有不平衡和周期波动性，导致传动系统振动传递到车身时引起汽车车身振动和噪声[1]。动力总成与车架之间通过悬置系统弹性连接，悬置系统的隔振性能好，发动机产生的振动只有小部分会传递到车身上。当汽车行驶在不平路面上时，由于悬置系统的作用，冲击力不会对发动机的使用性能和寿命造成影响。因此研究提高悬置系统的性能有着重大的实际意义[2-4]。国内外学者在基础性研究的支撑下，在理论试验研究方面，依据力学和振动知识优化设计悬置系统。以振动理论为基础，综合考虑人体对振动反应的敏感程度以及悬置系统刚体的模态、一阶弯曲振型及悬置系统弹性中心对悬置解耦的影响，提高悬置系统的综合性能，并研究悬置的隔振性能和参数匹配优化等问题；从整车的层面出发考虑汽车悬架等其它子系统的影响，搭建整车系统模型时，将建立好的动力总成悬置系统与汽车其它子系统装配，进行多目标的优化设计，取得了重要的经验和成果，但对于悬置系统限位功能的研究，还不够全面[5-10]。

本文以某动力总成悬置系统为研究对象，对动力总成悬置系统的性能进行仿真分析，分析悬置在有无阻尼状态下的减振情况，进而在考虑悬置系统阻尼特性情况下，优化悬置的刚度参数来减小支反力大小，从而降低振动的传递，减小动力总成悬置系统的振动。可提前预知系统性能的优劣，对性能比较差的悬置系统进行优化设计，进而保证汽车具有良好的NVH性能，避免重复性实物实验，从而节约开发成本和缩短周期。

1 动力总成悬置系统单自由度模型

动力总成悬置系统结构复杂，自由度多，为提高建模精度，需要对其进行一定的简化[11]，假设发动机各方向的振动相互独立，无干涉，针对各个方向的振动分别进行研究，本文研究的是发动机垂直方向的振动，以单自由度振动为例进行研究。

图1 悬置系统单向自由度的振动模型Fig.1 One-way degree of freedom virbration model of mounting system

图1为悬置系统的单向自由度振动模型。在模型垂向方向上作用激振垂直力的大小为f(t)=Fsin(w1t)，根据机械振动知识，模型的运动微分方程为[12]：

(1)

此方程的通解为：

(2)

在受到激励作用振动后，模型的作用力变为：

(3)

传递率TR为振动后传递的力的大小与外激励力的比值，在隔振分析中非常重要，由前面的计算结果得：

(4)

式中：m为系统质量，kg；c为阻尼系数，N·s/m；k为弹簧钢度，N/m；w1为外激振频率，rad/s；λ为频率比；w为固有频率，rad/s；ξ为阻尼比；cc为临界粘性阻尼系数。

令公式(4)中的阻尼比 为0.05、0.25、0.4、0.5、0.75，可得到传递率TR与频率 比之间的一系列曲线，如图2所示。

图2 传递率与频率比关系图Fig.2 Relational graph of transfer rate and frequency ratio

研究分析传递率与频率比关系图可知：

(1)前阶段，传递率随频率比值的变大有较大的上升，频率比值 的大小约等于1时，达到最大输出振幅，此时外激励频率与系统固有频率相接近，称该点为共振点；

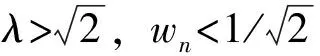
2 动力总成悬置系统建模与仿真分析

2.1 建模参数

本文研究的悬置系统为前悬置布置角度为48°、后悬置布置角度为45°的四点斜置的四缸四冲程发动机。其动力总成的质心位置、质量和转动惯量参数见表1；各悬置的位置和刚度参数见表2；各悬置的安装角度见表3。

表1 动力总成质心位置、质量和转动惯量参数

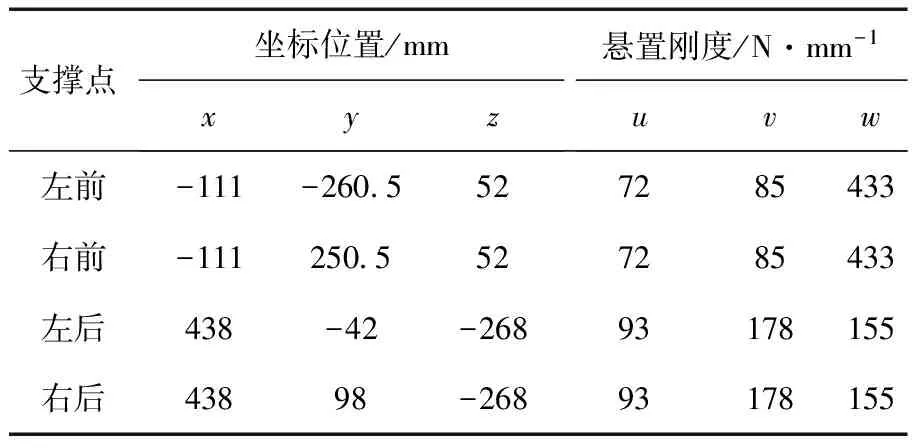
表2 悬置位置和刚度参数

表3 悬置安装角度

2.2 ADAMS仿真分析

研究工具利用多体动力学仿真软件ADAMS中的ADAMS/Vibration[13]频域分析模块对悬置系统进行动态仿真得到模态的振动解耦情况和频率分布情况。动力总成悬置系统仿真模型受迫振动得到的模态频率会以振动的形式在有效频率区域显示出来，震动结束后，可以得到元件初始的固有频率和相对应的模态能量分布状况，结果见表4。

表4 悬置系统固有频率和能量分配百分比

分析表4可知：

(2)振动耦合现象严重。沿Z轴方向和绕X轴方向的振动解耦率分别为56.93%和52.61%，比设计要求规定的90%低很多；X方向的解耦率为73.74%，其余方向的解耦率均低于57%，也比设计要求规定的80%低很多；振动占优方向不明显，各向振动之间存在严重耦合现象。

根据仿真分析结果，动力总成悬置系统的隔振性能较差，有必要进行优化设计，以提高各阶模态的解耦率和合理分布系统的固有频率[14]。

3 基于MATLAB的动力总成悬置系统优化分析

3.1 选定目标函数

根据实际工程经验，本文运用MATLAB软件，将能量解耦率作为优化目标进行优化设计[15]。动力总成悬置系统优化目标为系统能量解耦率，EP(i，n)表示动力总成悬置系统作n阶主振动时，第i个广义坐标上的能量占总振动能量的百分比，系统能量解耦率越高，EP(i，n)的值越大[15]，由于Matlab优化工具箱中的fgoalattain函数只能求目标函数的最小值，因此系统的能量解耦目标函数可确定为：

(5)

本文研究的悬置系统在6个振动方向上的解耦率分布目标值见表5。发动机垂向(z向)的不平衡力以及绕曲轴方向(θX向)的扭矩波动是发动机的主要激振方向，这两个方向振动的耦合程度增大将影响悬置系统的减振性能，所以设计动力总成悬置系统要求解耦率至少为90%，其它方向为80%。

表5 悬置系统解耦率目标值

3.2 选取设计变量

设计过程中，可以调整和优选的参数变量称为设计变量[16]。实际工程中，通常不将悬置元件的支承位置与角度作为设计变量，由于改变悬置的位置和角度，发动机上的安装位置也得改变，这样会增加制造成本，而且发动机的安装不能轻易改变。因此，优化设计动力总成悬置系统时，一般将悬置元件的主轴刚度作为优化设计变量，本文研究的动力总成悬置系统有4个悬置元件，每个元件具有三个主轴刚度，则优化设计变量有12个。

3.3 确定约束条件

悬置元件的主轴刚度作为优化时的设计变量，其变化需在一定范围之内。刚度值太小，受力时容易变形造成疲劳损坏，缩短使用寿命，而且动力总成在极限工况下会与周围零部件发生碰撞，影响其使用性能；悬置元件的刚度值太大，其振动传递率大，减振性能不好，导致汽车的乘坐舒适性差。根据工程经验，优化设计时，本文的动力总成悬置元件各主轴刚度值允许的变化范围见表6。

表6 悬置主轴刚度约束范围 N·mm-1

此外系统的固有频率也需满足一定条件。为了避免路面的激励引起共振，系统固有频率最低需要大于5Hz。本文研究的动力总成悬置系统固有频率范围为6～17Hz。为避免各向引起共振，要求各方向上的频率差大于1Hz。

3.4 MATLAB优化求解

在MATLAB中，多目标问题的标准形式为[7]：

minimizeγ

sub.toF(x)-weight·γ≤goal

C(x)≤0

Ceq(x)=0

A·x≤b

Aeq·=beq

lb≤x≤ub

其中：x、b、beq、lb、ub为向量，A、Aeq为矩阵，F(x)、C(x)、Ceq(x)为返回向量的函数，weight是权值系数向量，goal为目标函数目标值，γ为松弛因子标量。

运用MATLAB中的优化工具箱对动力总成悬置系统进行优化求解，首先输入动力总成的质量和惯量、悬置元件的位置参数和安装角度，得到动力总成悬置系统的质量矩阵、位置转移矩阵和方向转移矩阵，进而计算出系统的固有频率和解耦率；然后根据输入的优化设计变量及其变化范围等，优化得到各自由度解耦率达到目标值时最优解，输出最终优化结果和此时的设计变量(悬置元件刚度)值。

进行动力总成悬置系统优化设计时，由于目标函数(系统的能量解耦率)和约束条件(固有频率)都不能直接用设计变量(悬置刚度)表达，需要另外编写能量解耦率的目标函数程序Optgoal.m和固有频率的约束条件程序constraint.m。本文利用软件MATLAB中的foalattain函数进行优化计算，其用法为[17]：

[x，fval]=fgoalattanin(′fun′，x0，goal，weight)

[x，fval]=fgoalattanin(′fun′，x0，goal，weight，A，b)

[x，fval]=fgoalattanin(′fun′，x0，goal，weight，A，b，Aeq，beq)

[x，fval]=fgoalattanin(′fun′，x0，goal，weight，A，b，Aeq，beq，lb，ub，nonlcon)

通过迭代运算编写MATLAB优化计算程序，获得优化后的各悬置刚度值，各悬置刚度值见表7，系统的固有频率和振动解耦情况见表8，优化前后分析结果对比见表9。

表7 优化后各悬置刚度参数

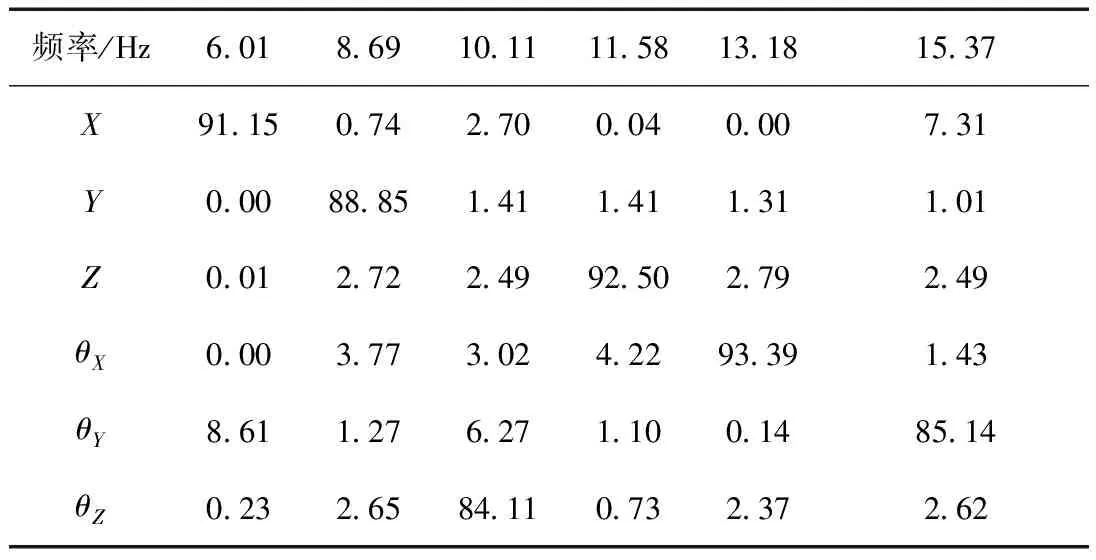
表8 优化后悬置系统固有频率和能量分配百分比

表9 优化前后分析结果对比

对比优化前表2与优化后表7可知，优化后动力总成两个前悬置元件的主轴刚度大于优化前，而两个后悬置优化后主轴刚度都有所减小。提高悬置系统的减振性能，并不是简单地通过减小悬置的刚度，使悬置足够软，而是通过合理匹配各悬置元件的刚度值。

分析表8、表9可知：

(2)优化后，系统的能量解耦率显著提高。优化前，对振动影响较大的垂直方向和绕X轴转动的解耦率分别为52.03%和54.11%，优化后有明显提高，分别为92.5%和93.39%，达到了表5中振动解耦率的优化目标值；其它方向的振动解耦率也都大于80%，与优化前相比都提高很多，达到优化设计要求，动力总成悬置系统的减振性能得到改善。

(3)优化结果表明，通过调整悬置元件各主轴刚度，可以降低动力总成悬置系统的振动耦合，提高系统的解耦率，实现固有频率的合理配置，改善汽车的乘坐舒适性，达到了优化设计的目的。

4 总结

本文以应用广泛的橡胶悬置系统作为研究对象，研究其隔振和限位性能。分别利用软件ADAMS建立动力总成悬置系统三维模型和软件MATLAB编程，并对其进行了固有特性分析，得到系统的固有频率的分布情况和振动耦合率，结果表明系统的固有频率布置不合理、振动解耦率低，耦合情况严重，不满足设计要求，需进行优化设计。结合工程实际，运用MATLAB软件，利用能量解耦法，以动力总成悬置系统的解耦率为目标，以悬置元件的刚度为设计变量，对动力总成悬置系统进行优化设计，对优化前后的系统固有频率和各阶模态能量分布进行对比分析，结果表明所优化的悬置系统实现了固有频率的合理配置以及提高了振动解耦率，达到了优化的目标。本文在优化设计动力总成悬置系统时，只将系统解耦率作为优化目标函数，在后续的研究中，可以考虑悬置点的支撑反力等，选取多个目标函数进行优化设计。

[1]余天超，孙永厚，刘夫云.发动机橡胶隔振器动特性分析[J].机械设计与制造，2013，51(12)：235-237.

[2]沈颖刚，杨文钊，郭鹏，等，张俊红.汽车悬置系统研究综述[J].机械设计与研究，2015，31(6)：131-139.

[3]焦东明，郑明军，陈军伟.汽车液阻悬置动特性和隔振性能分析[J].噪声与振动控制，2011，31 (6)：127-130.

[4]赵金鹏，潘旭磊，闫青，等.发动机隔振及其传递率计算的试验研究[J].建筑机械化，2013，34 (3)：54-56.

[5]李玉桂.动力总成悬置系统的布置设计与解耦优化[J].机电技术，2012，36 (1)：49-53.

[6]吴杰，刘玉波.动力总成悬置系统固有频率和解耦率的区间分析方法[J].噪声与振动，2012，32 (3)：12-15.

[7]Pan G Y，Yang X，Yan Y.Optimization of Vehicle Powertrain Mounting System and its Performance[J].Applied Mechanics and Materials，2014，441：580-583.

[8]Hassison H C.Engine Installation[J].Automobile Engineering，2009，10：46-50.

[9]Angrosch B，Plochl M，Reinalter W.Mode Decoupling Concepts of an Engine Mount System for Practical Application[J].Proceedings of the Institution of Mechanical Engineers Prt K Journal of Multi-body dynamics，2015，229(4)：331-343.

[10]赵旭光，姜潮，于盛.汽车发动机悬置系统的多目标优化[J].机械科学与技术，2015，34(12)：1940-1946.

[11]陈 克，李晓政，周霜霜.动力总成悬置系统优化与减振分析[J].沈阳工业大学学报，2016，38(1)：57-62.

[12]张 怡，饶建强，陈吉清.皮卡车动力总成悬置系统隔振特性优化[J].汽车工程学报，2016，6(3)：181-186.

[13]Wang H G，Wu X Q，Wang LP，et al.Study on Motion Simulation Method of Parallel Mechanism Based on ADAMS[J].Applied Mechanics and Materials，2013，2607(389)：590-595.

[14]张要思.减振体参数范围对动力总成悬置系统刚体振动抑制关系研究[D].合肥：合肥工业大学，2014.

[15]Lee J H，Singh R.Critical Analysis of Analogous Mechanical Models Used to Describe Hydraulic Engine Mounts[J].Journal of Sound and Vibration，2008，311(3)：1457-1464.

[16]张超.车辆动力总成悬置系统匹配优化仿真研究[D].重庆：重庆交通大学，2011.

[17]Benner P，Kressner D，Sima V，et al.Die SLICOT-Toolboxen für Matlab(The SLICOT Toolboxes for Matlab)[J].At-Automatisierungstechnik，2010，58(1)：470-476.

Vibration Isolation Performance Simulation and Optimization of Vehicle Powertrain Mounting System

Fan Pan1，Bao Hanwei2

(1.School of Computer Science and Technology，Baoji University Of Arts and Sciences，Baoji 721016；2.Shinva Medical Instrument CO.Ltd，Zibo 255000)

In order to solve the problem of vibration isolation in vehicle powertrain mounting system，the 6 degree of freedom analysis model of powertrain mounting system was established.The key parameters that affected the vibration isolation were analyzed.According to the calculation theory of inherent characteristics of mounting system，dynamics simulation model was established with ADAMS software and inherent characteristics was analyzed with MATLAB to get the system frequency and energy decoupling rate.And then，taking the energy decoupling rate as the goal，the spindle mounting stiffness as the optimization variable，the mounting system was optimized with the optimization function in MATLAB.The results showed that he improved mounting system vibration isolation rate had increased significantly，and the isolation performance had been improved.Adjusting the spindle mounting stiffness can reduce the vibration coupling of the powertrain mounting system，improve the decoupling rate and realize the reasonable configuration of the inherent frequency.

Powertrain；mounting system；vibration isolation；energy decoupling

2017-04-01

宝鸡文理学院校级重点科研项目(ZK16110)；2016年中央高校科研业务费基础研究计划项目(310822161125)

樊攀，硕士，助教。研究方向：汽车结构与CAE。E-mail：249918348@qq.com

樊攀，包汉伟.汽车动力总成悬置系统隔振特性仿真优化[J].森林工程，2017，33(4)：89-93.

U 463.3

A

1001-005X(2017)04-0089-05