小改编，大不同——一道课本习题的改编历程

广东省惠州市惠阳区沙田中学 张 贝

小改编，大不同
——一道课本习题的改编历程

广东省惠州市惠阳区沙田中学 张 贝

一、改编题的来源

初中数学教材中有许多习题都蕴含着重要的数学思想和方法，对数学解题具有一定的导向作用，每一道课本习题都是经过编者不断推敲﹑揣摩的，蕴含着他们大量的心血。课本习题的教学是巩固学生双基﹑培养学生思维能力﹑提高学生解题能力的一条重要渠道，教学中，我们要善于对习题进行合理的变化和挖掘，我们将其改编是丰富原题内涵的有效途径，同时，在教学中将教材中的典型例题进行改编，既能够激发学生的学习兴趣，又能培养学生发现问题和解决问题的能力。我查找了平时教学中积累的典型习题，查阅了相关资料及近几年各地的中考题，特别是广东近几年的中考题，它们都是进行改编题的第一手资料。我最终选择以下习题进行改编，原题选自人教版《数学》（2009年3月第2版）九年级上册第24章第123页第14题。

原 题： 如 图1， ⊙O的 直 径AB=12cm,AM和BN是它的两条切线，DC切⊙O于E，交AM于D，交BN于C。设AD=x，BC=y，求y与x的函数关系式，画出它的图象。

图1

分析：本题以学生熟悉的圆与直角梯形为知识载体，主要突出对本章所学的核心概念（切线）和数学定理（切线性质及切线长定理）进行考查，涉及的知识点是最基础﹑最核心的数学知识。特别是图中所需的辅助线的构建，对发展学生的抽象思维，借助数学直观提炼基本图形所隐含的性质和结论有着重要的作用。

二、改编历程

1.初稿

如图2，⊙O的直径AB=12cm,AM和BN是它的两条切线，DC切⊙O于点E，交AM于D，交BN于C,设AD=x，BC=y。

（1）求y与x的函数关系式；

（2）用含x的式子表示求图中阴影部分的面积S。

解：（1） 如 图 2， 过 点 D作DF⊥BC于点F，

∵AM和BN是⊙O的两条切线，DC与⊙O相切,

∴AD=DE=x,BC=EC=y,

在Rt△DFC中， ,

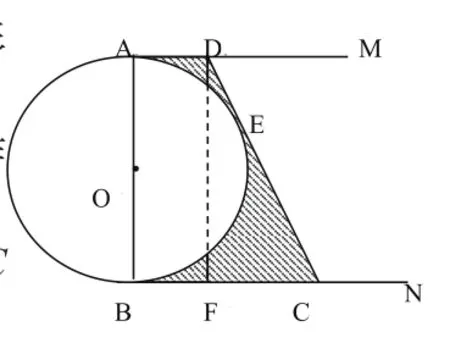
图2

反思：课本习题考查的知识点较单一，综合性不强。改编后的题在图形上没有多大的变化，只是再添加了阴影部分，条件上没有增加新的条件，只是简单增设了一问。此题较原题就考查内容上有所丰富，增加考查了不规则图形的面积求法，涉及的知识点多，体现了一定的层次性针对。针对增加的第（2）问，在解答时发现，第（1）问为第（2）问解答做了铺垫，降低了题目的难度，使不同层次的学生的思维都得到了锻炼。习题中设问（1）（2）之间采取的是递进式的结构，采用递进式的结构能挖掘问题的深度。

2.磨稿

改编稿1：

如图2，⊙O的直径AB=12cm,AM和BN是它的两条切线，DC切⊙O于点E，交AM于D，交BN于C,设AD=x，BC=y。

（1）求y与x的函数关系式;

（2）用含x的式子表示图中阴影部分的面积S;

（3）当x，y满足何种关系时，S取得最小值？并求出最小值。

解：（1）如图2过点D作DF⊥BC于点F，

∵AM和BN是⊙O的两条切线，DC与⊙O相切,

∴AD=DE=x,BC=EC=y,

在Rt△DFC中，

反思1：此题在初稿的基础上增加了一问，增加的第（3）问让问题的设计变得更加有梯度，起到了引导学生思维的作用，增加的这一问仍然采取的是递进式的结构，巧妙地借助了设问（1）（2）的结论来解答，但美中不足的是在解（3）的时候用到了均值不等式，而这个内容在初中阶段来说是有超纲之嫌。

改编稿2：

如图2，⊙O的直径AB=12cm,AM和BN是它的两条切线，DC切⊙O于E，交AM于D，交BN于C,设AD=x，BC=y。

（1）求y与x的函数关系式；

（2）用含x的式子表示图中阴影部分的面积S。

（3）连接BE,当x为何值时，△BCE为等边三角形？并求当△BCE为等边三角形时图中阴影部分的面积。

解：（1）过点D作DF⊥BC于点F，

∵AM和BN是⊙O的两条切线，DE与⊙O相切，

∴AD=DE=x,BC=EC=y，

在Rt△DFC中， ，

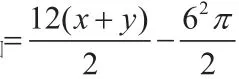
（3）连接OE,过点O作OG⊥BE。

∵△BCE为等边三角形，∴∠EBC=60°，∴∠OBG=30°，在Rt△OGB中,

反思2：因为在改编稿1中的第（3）问存在超纲的嫌疑，所以在改编稿2中我否定了这种设问，再次改编后的（3）能够与（1）和（2）有更加紧密的联系，围绕着初中数学中常见﹑常考的等边三角形这个知识点，改编稿2继续进行着递进式结构，紧紧围绕着中考考纲，尽可能全面地考查学生的知识结构和能力。

总之，课本习题是编者精心设计和挑选的，具有典型性和探索性，所隐含的内容也相当丰富，现在很多中考题都能在课本中找到其原形。因此在教学中，教师要重视教材，吃透教材，钻研教材，加强对课本习题的挖掘，灵活使用习题，通过一题多变﹑一题多解把问题弄透，达到触类旁通﹑举一反三的效果，从而进一步提高学生的解题能力和探究能力，使教学达到“事半功倍”的效果。

book=93,ebook=95