高中数学解题中隐含条件的挖掘

江苏省启东市吕四中学 刘 瑾

高中数学解题中隐含条件的挖掘

江苏省启东市吕四中学 刘 瑾

在数学解题过程中，不少学生容易忽视题中的隐含条件，感觉题目难解。实际上，数学题虽然灵活多变，但若能发掘出其中的隐含条件，就能更好地解锁解题过程，将复杂问题简单化，降低解题难度，快速而准确地解题，这样，学生对数学的学习信心也会进一步得到保持与提升。

一、观察题目结构，挖掘隐含条件

面对数学问题时，学生需要具备较强的洞察力，反复研读题目，多向思索，迅速判断题中是否有无隐含条件，找出问题本质，快速得解。其中，明确题目结构特点，再根据所学知识合理推断有关数学公式或者所应用的几何模型，是发掘题中隐含条件的一种重要方式。对此，教师要引导学生引起注意，从而提高数学解题能力。

二、注意数形结合，发现隐含条件

在解答高中数学题目时，学生有时候会遇到这样的情况：直接利用题目给出的已知条件来解题比较困难，而那些可以快速解题的有效条件却隐藏于题中蕴含的图形中，若能够认真观察，由图形来获取隐含条件，则可以找到解题的切入点与突破口，将抽象问题形象化，将繁杂问题简明化。所以，教师要指导学生数形结合，学会认真分析所给图形极其条件，由图形特征去发掘一些隐含条件，简化解题过程，或者利用转化思想，适当添加辅助图形，实现数形结合，再由图形中获取含而未漏的重要条件，将问题迎刃而解。

例如：平面上有两点A（-1，0）﹑B（1，0），在圆(x-3)2+(y-4)2=4上取点P，请求出使AP2+BP2取最小值的时候点P的坐标。

对于这一题目，不少学生运用常规方法，列出目标函数y=AP2+BP2,再求解最小值。这一方法过程比较烦琐，而且容易出现错误。实际上，通过画出相关图形（如图1所示），再根据三角形中线性质，就能获得隐含条件： 。因此，当OP有最小值的时候，AP2+BP2也有最小值。此时，就很容易看出点O和圆心（3,4）的连线与圆的交点就是要求的点P的坐标。因此联立方程，则有：

三、重视数学性质，发掘隐含条件

在解数学问题时，数学概念﹑性质或者定义是基本知识与前提条件，但运用的方式有所差别，或直接运用，或者间接运用，所以在解题教学中，教师要善于引导学生从数学定义（概念）入手，认真分析与推敲，深挖隐含条件，化隐为显，快速解答。

四、学会类比联想，挖掘隐含条件

在高中数学做题时，有时会遇到这样的题目：无法发现已知条件和所求问题的联立关系，也没有可以直接用于类比的定理或者公式。这就需要由联想与类比入手，深挖出题目隐藏的有用条件，抓住解题契机，快速而准确地做答。

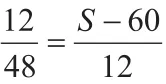
五、根据已知条件，发现隐含条件

在有些数学题目中，隐藏的条件往往在已知条件里面，需要结合已知条件进行灵活衍生。因此，在解答高中数学题时，如果感觉没有充足的解题条件，同时题设中又很难发现隐含条件，此时就需要结合已知条件，运用列举分析或者图形等方式，获取含而不露的解题条件，化难为易。

例如：已知实数x，y满足x2+y2-2x+4y=0，请求出x-2y的最值。

根据已知条件，进行配方，使之转化成：(x-1)2+(y+2)2=5，即圆心坐标是(1,-2)，半径是的圆（如图2），圆方程经过坐标原点（0，0）；另外，表明圆(x-1)2+(y+2)2=5上的点到原点距离的平方的一半。再由数形结合入手，就能发现最小值是0，最大值是10。

总之，隐含条件是解数学题的重要因素与有效利器。在平时教学中，教师要注意加强训练，引导学生探寻与积累多样解题方法和技巧，或深钻数学定义去深挖，或在类比联想中去发现，或从数形结合中去发掘，或抓住题目结构来获取隐含条件，不断强化自己的观察能力﹑思考能力，提升数学解题水平。

图2

book=79,ebook=81