从数学中考谈创新思维的培养

江苏省泰州市口岸实验学校 孙友权

从数学中考谈创新思维的培养

江苏省泰州市口岸实验学校 孙友权

中考作为学生学习生涯的重要阶段，是未来方向选择一个很大的决策点，数学作为中考中的主要考试科目，其分量非常重要。近年来一直提倡教育改革，教育要求培养并提高学生的创新思维，数学课堂将不再只是注重数学知识的学习，还要重视学生的创新思维能力的发展。文章就如何在数学中考中培养创新思维进行探讨。

初中数学；中考；创新思维

创新思维能力的培养，表明教学目的已经从知识教育转向素质教育，这种能力的培养可以提高学生的学习主动性和积极性，开发学生的内在潜力。数学中考是学生三年初中数学学习生活的一个全面总结和检验，有很大的借鉴意义。在数学中考中，依靠多年来的经验，从教师和学生两方面入手，通过不同的角度和不同的思维方式进行全面的研究，寻找培养学生创新思维的方法。

一、教师创建情境思考模式，培养学生的创新思维能力

初中是学生人生中的一个重要阶段，在中考考场上，由于学生的知识掌握程度不同，应对考试的心理素质不同，考出的结果也不相同。其中，最令人惋惜的是有良好的学习能力但是由于心理素质差导致无法其取得满意的成绩。为了提高学生的应试能力，教师可以参考中考数学考试规则，模拟考试情境，锻炼学生的心理素质，提高应试能力。而借由中考，不仅可以从中考的考试模式设置情境，也可以通过其中的具体试题，如在学习不等式时，由现实情况模拟改编，贴近生活，帮助学生寻找解决方法。

例1 一企业为了适应市场经济需要，决定进行人员结构调整，该企业现有生产型行业人员100人，平均每人全年可创造产值a 元，现欲从中分流出x人去从事服务型行业。假设分流后，继续从事生产型行业的人员平均每人全年创造产值可增加20%，而分流从事服务型行业的人员平均每人全年可创造产值3.5a元，如果要保证分流后，该厂生产型行业的全年总产值不少于分流前生产型行业的全年总产值，而服务型行业的全年总产值不少于分流前生产型行业的全年总产值的一半，则分流后从事服务型行业的人数为多少？

解析：设分流后从事服务型行业的人数为x，则由题意得：

（100-x）·（1+0.2）·a3.5a·x≥12·100a，

解得14.27≤x≤16.23。

因为x为正整数，所以x为15或者16。

由上面这道题可知，提出比较贴近生活的题目，学生在认知上会有亲切感，并对解题产生兴趣，可以帮助学生更好地展开思考，进而培养学生的创新思维能力。

二、教师注重培养学生的理解能力和表达能力，培养学生的创新思维能力

数学不仅仅是数字的学科，还涉及文字类的学习，例如数学知识点的定义，还有应用题等，都需要学生有良好的理解能力，只有做到理解基础，才能更好地表达自己的观点，最终达到培养学生的创新能力的目的。

例2 在某个变化过程中，有两个变量x﹑y，如果给x一个值，y即有唯一与之确定的值，那么x就是自变量，y叫作x的函数。

这段关于函数的定义，就是在解释函数中x﹑y两个值的关系，但是学生在学习这个章节时并不容易理解，这时就需要教师在平常的教学中，通过具体的实例（如小明买卡片，一张卡片1.2元，小明买的张数和他应该付的钱呈函数关系）引导学生反推这个定义，由原本的已知定义变成未知定义，又推导定义，最后确定定义。这个过程中，学生的理解能力得到了锻炼，同时在反推定义的同时，也锻炼了学生的表达能力，学会了如何精炼地总结语言，而这两种能力的提升，也为培养学生的创新思维能力提供帮助。

三、教师通过具体的例题，培养学生的创新思维能力

近年来，数学中考的考试方向主要在于考验学生的逻辑思维能力﹑运算能力﹑创新能力﹑空间几何能力等。如初中的几何题，虽然最终的答案只有一个，但是验证过程可以运用多种方法解答，这就是在测验学生的创新能力和思维能力。

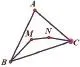
例3 已知M﹑N为△ABC内两点，求证：AB+AC＞BM+MN+ CN。

证法1：将MN延长，分别交AB﹑AC于F﹑E ，

因为 在△AFE中， AF+ AE＞FM+MN+EN，

在△BMF中，FB+FM＞BM，

在△CNE中，CE+EN＞CN，

所以AF+AE+FB+FM+CE+NE＞FM+MN+NE+BM+CN，

所以AB+AC＞BM+MN+CN。

证法2：延长BM交AC于G，延长CN交BG于K ，

在△ABG和△KGC和△KMN中，

因为AB+AG＞BM+MK+KG ，

GK+GC＞KN+CN，MK+KN＞MN ，

所以AB+AG+KG+GC+MK+KN＞BM+MK+KG+KN+CN+MN，

所以AB+AC＞BM+MN+CN。

通过上面例题的所述，同一道题因为添加的辅助线不同，证明的方式也不同，这就考验学生的创新思维能力，能否找出不同的关键点求解问题。数学中考中，每一分可能都是改变学生成绩排名的关键，学会多种解题方法，在解题时，若在某种思路上卡住无法继续时，就可以选择另一种解题思路，而这种能力在于平时的积累。从中考中总结经验，找寻提高成绩的方法，培养创新思维能力，又反馈到中考的实践中去，从而使学生取得良好的成绩。

四、借鉴数学中考多年经验，并总结题型结构，培养学生的创新思维能力

中考数学一般由选择题﹑填空题﹑计算题﹑解答题四大部分组成，其中解答题包括不等式组﹑几何题﹑统计题﹑二次函数题等。解答题的几个知识点试题的难度不一，其中压轴的一般是二次函数题，也是难度最大的题型。

例4 抛物线y=-x²+bx+c与x轴交于M(1,0),N(- 3,0)两点。（1）求该抛物线的解析式；（2）设（1）中的抛物线交y轴于E点，该抛物线的对称轴上是否存在点F，使得△FME的周长最小？如果存在，求出F点的坐标，如果不存在，请说明理由；（3）（1）中的抛物线上在第二象限那部分上是否存在一点G，使△GNE的面积最大？如果存在，求出点G的坐标及△GNE面积的最大值，如果没有，请说明理由。

如上述例题所示，中考压轴题的难度一般是这种等级，教师需要按照等比量的难度训练学生的做题量，而在学习中，教师要尽量鼓励学生学会自主探讨，让学生先自由讨论，说出解题思路，然后再公布答案，让学生发现自己的不足之处，补充添加，在解题中培养锻炼学生的创新思维能力。

从中考中总结经验，教师通过自己的方法创造情境模拟训练，同时加强学生各方面能力的培养，如理解能力和表达能力，为培养学生的创新思维能力做铺垫，然后有计划地模拟中考的考试题型和考试难度，训练学生的应试能力，发散思维，提高他们的解答能力，并最终服务于中考，提高学生的中考成绩。

book=84,ebook=86