基于ADPSO算法优化LSSVM的高速公路交通量预测方法
司文静,封喜波,耿立艳,张占福(.北华航天工业学院 建筑工程系,河北 廊坊 06000;.河北省高速公路廊坊北三县管理处,河北 廊坊 06000;3.石家庄铁道大学 经济管理学院,河北 石家庄 00043;4.曼彻斯特城市大学 商学院,曼彻斯特 英国 M 6BH;.石家庄铁道大学 四方学院,河北 石家庄 03)
基于ADPSO算法优化LSSVM的高速公路交通量预测方法
司文静1,封喜波2,耿立艳3,4,张占福5
(1.北华航天工业学院 建筑工程系,河北 廊坊 065000;2.河北省高速公路廊坊北三县管理处,河北 廊坊 065000;3.石家庄铁道大学 经济管理学院,河北 石家庄 050043;4.曼彻斯特城市大学 商学院,曼彻斯特 英国 M15 6BH;5.石家庄铁道大学 四方学院,河北 石家庄 051132)
针对高速公路交通量与其经济影响因素之间的复杂非线性关系,将最小二乘支持向量机(least squares support vector machines,LSSVM)与自适应动态粒子群优化(adaptive dynamic particle swarm optimization,ADPSO)算法相结合,提出一种ADPSO算法优化LSSVM的高速公路交通量新型预测方法.将建模简单、精度高的LSSVM作为预测模型,通过寻优能力优异的ADPSO算法选择LSSVM最优参数.以某市高速公路交通量为例验证模型的有效性.结果表明,所提方法的预测性能较好,适合于高速公路交通量的短期预测.
高速公路;交通量预测;自适应动态粒子群优化算法;最小二乘支持向量机
高速公路交通量的准确预测是高速公路规划与设计的重要基础工作.由于高速公路交通量往往与某一区域的社会经济发展水平联系紧密,经济因素是影响某地区高速交通量的主要因素,而经济影响因素对高速公路交通量的作用形式不同,这就使得高速公路交通量与其经济影响因素之间存在复杂的非线性关系.高速公路交通量预测方法中,较早使用的方法主要有四阶段法[1]、时间序列预测法[2]、灰色预测法[3]等.四阶段法需要大量的调查数据,不适合大规模应用.时间序列预测法和灰色预测法均为单变量预测模型,计算简单且易于实现,但难以揭示高速公路交通量与经济影响因素之间的复杂非线性关系.
近年来,神经网络被引入到高速公路交通量预测中.神经网络是一种数据驱动的非参数预测方法,可灵活反映高速公路交通量与经济影响因素之间的复杂非线性关系,取得了较好的预测效果[4].神经网络以经验风险最小化为基础,在实际应用中容易遇到局部极优值、过拟合等问题,而且需要大量的数据样本进行网络训练.作为一种基于统计学习理论和结构风险最小化原则的学习算法[5],支持向量机(support vector machines,SVM)较好地解决了神经网络的大样本训练问题,具有良好的非线性拟合能力和泛化能力,在数据样本较少的情况下依然能获得较高的交通量预测精度[6-7].由于SVM需求解二次规划方程,使用的样本数量越多,SVM的计算复杂程度越高.最小二乘支持向量机[8](least squares support vector machines,LSSVM)是一种以SVM为基础的学习算法,它将最小二乘线性系统作为损失函数,简化了计算过程,提高了求解速度[9-10],更适合于高速公路交通量预测研究.LSSVM的性能依赖于自身参数的选择,传统参数选择方法大多具有主观性,难以达到满意的预测效果.在众多智能优化算法中,粒子群优化(particle swarm optimization,PSO)算法由于具有实现简单、寻优效果好等特点[11],在LSSVM参数选择方面的有效性已得到证明.传统PSO算法中,惯性权重、加速系数的取值对算法的优化性能起到非常重要的作用.国内外学者对这2个参数进行了不同的修正,形成了不同的改进PSO算法,其中,有代表性的有基于惯性权重自适应调整的自适应惯性权重粒子群优化(adaptive inertia weight particle swarm optimization,AIWPSO)算法[12]和基于加速系数动态调整的动态加速系数粒子群优化(dynamic acceleration coefficients particle swarm optimization,DACPSO)算法[13],这2种改进PSO算法均在一定程度上改善了传统PSO算法的寻优效率.为进一步提高PSO算法的寻优能力,本文基于这2种改进PSO算法,提出自适应动态粒子群优化(adaptive dynamic particle swarm optimization,ADPSO)算法,并利用ADPSO算法选择LSSVM最优参数.通过对高速公路交通量的实例计算,验证该方法的有效性.
1 最小二乘支持向量机
LSSVM是SVM的一种改进形式,将标准SVM中的不等式约束条件转换为等式约束条件.设有N组训练样本{(xk,yk)|k=1,2,…,N},其中,xk∈Rd为d维输入向量,yk∈R为对应的一维输出.LSSVM函数估计的优化问题如下:
(1)
其中,φ(x)为一非线性映射函数,用于将原始输入数据映射到高维特征空间;ω、b分别为权重向量与偏差常量;γ为正则化参数;ek∈R为误差变量.利用拉格朗日法求解上述优化问题,首先构造优化问题对应的拉格朗日函数,如下所示:
(2)
其中,α=[α1,…,αN]T为拉格朗日乘子向量;然后分别求解拉格朗日函数(α,ω,b,e)对αk、ω、b、ek的偏导数,从而将优化问题(1)转化为求解一组线性方程,如下:
(3)
其中,1N为N阶列向量,其中的元素都为1;为IN阶单位矩阵;Ω为N×N阶矩阵,其元素为Ωk=K(x,xk)=ø(x)Tø(xk),K(x,xk)为满足Mercer条件的核函数;Y=[y1,…,yN]T.由式(3)求出a和b后,可得到LSSVM回归模型为
b.
(4)
选取泛化能力强的RBF核函数作为LSSVM核函数,则式(4)转化为
‖x-xk‖2/σ2)]+b,
(5)
其中,σ为核函数参数.
2 自适应动态粒子群优化算法
惯性权重δ和加速系数c1、c2是影响PSO算法性能的2个重要控制参数,它们的取值直接影响到算法的搜索能力和收敛速度,其中,δ描述了粒子上一步迭代的速度对当前速度影响的程度.δ取值越大,粒子的速度越大,有利于粒子发现新的解域,算法的全局搜索能力越强;δ取值越小,粒子的速度越小,有利于粒子在当前空间搜索更优解,算法的局部搜索能力越强.目前采用较多的惯性权重是线性递减策略,其值随着迭代次数的增加而线性减小.线性递减策略虽可一定程度上平衡全局搜索能力和局部搜索能力,但粒子的实际搜索过程是一个非线性过程,该策略难以正确反映粒子的真实搜索过程,而且线性递减策略无法考虑适应度函数提供的信息,将导致粒子搜索方向的启发性不强,使得算法的搜索速度较慢而易陷入局部最优值[14].c1、c2反映了粒子自身认知信息与社会认知信息的交流程度.迭代前期阶段,希望c1取值较大、c2取值较小,便于粒子进行全局寻优、避免陷入局部极值;迭代后期阶段,应有c1取值较小、c2取值较大,使粒子迅速、准确地收敛于全局最优解.传统PSO算法中,c1、c2取相同的固定值,粒子的自身认知能力与社会认知能力相同,算法在迭代初期虽可保持较快的收敛速度,但到迭代后期,由于粒子逐步统一化,容易陷入局部最优.
惯性权重、加速系数两参数相辅相成,共同影响着PSO算法的寻优能力.若对它们单独进行调整,将削弱粒子搜索过程的统一性,难以适应复杂非线性问题的优化.ADPSO算法采用自适应动态调整策略,使惯性权重与加速系数同时随适应度值变化,以增强粒子的全局搜索能力与局部搜索能力、获得更优的搜索结果.
假设在D维目标搜索空间中,有一个由m个粒子组成的群体,每个粒子代表所优化问题的一个潜在解,第i个粒子的位置记为Si=(si1,…,siD),其速度记为Vi=(vi1,…,viD).在整个种群中,每个粒子通过目标函数的适应度值搜索个体最优位置Pibest=(si1best,…,siDbest)和整个粒子种群的最优位置,也就是全局最优位置Gbest=(s1best,…,sDbest).每个粒子的速度与位置按以下公式更新:
(6)
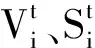
(7)
其中,δmax、δmin分别为惯性权重的最大值与最小值,F为粒子的当前适应度值,Favg、Fmin分别为粒子群的平均适应度值与最小适应度值.由式(7)可知,当F高于Favg时,应取较大的δ值,使粒子更快地飞向更优的目标搜索空间;当F低于Favg时,应取较小的δ值,使粒子在当前目标搜索空间中寻找更优位置.
c1和c2为加速系数,这里设为随着适应度值进行动态更新,更新公式为
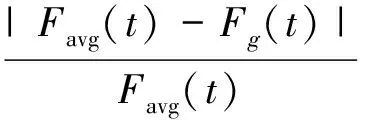
(8)
c2(t)=4-c1(t),
(9)
其中,Favg(t)为粒子第t步迭代的平均适应度值;Fg(t)为种群第t步迭代的最优适应度值;c1(t)、c2(t)的取值在[0,4]之间.根据式(8)和式(9),迭代前期阶段,Favg(t)与Fg(t)的差异较大,可获得较大的c1(t)值、较小的c2(t)值,便于粒子进行全局搜索、免于陷入局部最优值;迭代后期阶段,Favg(t)与Fg(t)的差异较小,可获得较小的c1(t)值、较大的c2(t)值,有利于增加粒子的多样性,提高算法的收敛速度与搜索精度.
3 LSSVM-ADPSO模型
由式(3)和式(5)可知,基于RBF核函数的LSSVM有2个参数需要确定:正则化参数γ和核参数σ,γ用于协调LSSVM的误差与复杂程度,σ反映了数据样本的范围特性.参数组合(γ,σ)的合理选取对提高LSSVM的学习能力与泛化能力至关重要.传统参数确定方法,如经验法、试凑法、网格分割法、交叉验证法等需要进行大量计算,且具有人为选择的盲目性,将使得LSSVM收敛速度减慢,难以得到最优解.本文采用ADPSO算法选择LSSVM最优参数.
利用ADPSO算法选择LSSVM最优参数(记作LSSVM-ADPSO模型),本质上是将LSSVM的构建过程与ADPSO算法的寻优过程有机融合,以每个粒子代表LSSVM的一组参数组合(γ,σ),在(γ,σ)构成的二维目标搜索空间中,粒子群通过目标函数确定的适应度值来搜寻全局最优解.LSSVM-ADPSO模型构建及预测的具体步骤如下:
步骤1 数据标准化处理.对原始样本数据进行标准化处理,计算公式如下:

(10)
其中,θmax、θmin分别为原始样本数据的最大、最小值;θ、θ′分别为标准化前、后的数据样本.将θ′划分为训练样本集L与验证样本集Z2部分.
步骤2 粒子群初始化.设置粒子群的各种参数,如种群规模数m,惯性权重的最大值与最小值δmax、δmin,最大迭代步数tmax等.随机给出粒子的初始速度与初始位置,粒子位置对应LSSVM的参数组合.
步骤3 适应度函数定义.将L划分为训练样本子集U和检验样本子集V,定义适应度函数为LSSVM的训练误差与检验误差之和,如下:
(11)
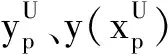
步骤4 粒子群最优位置更新.根据式(11)计算粒子i的适应度值,比较粒子i的当前适应度值与自身最优适应度值,若更优,更新粒子的个体最优位置为当前位置;比较每个粒子的个体最优位置适应度值与种群最优位置适应度值,若更优,更新种群的最优位置为该粒子的个体最优位置.惯性权重δ按式(7)更新,加速系数c1(t)和c2(t)分别按式(8)与式(9)更新.
步骤5 终止条件判断.若满足期望误差或预设的迭代步数,则停止搜索,粒子群的全局最优位置即为LSSVM的最优参数组合(γ*,σ*);若不满足要求,转回步骤3,进行新一轮搜索.
步骤6 模型构建与预测.根据最优参数组合(γ*,σ*)建立LSSVM并预测高速公路交通量,再将预测值转化为原始高速公路交通量预测值,转化公式如下:
(12)
4 实例计算
4.1 指标选取
以某市高速公路交通量为例,验证LSSVM-ADPSO模型的有效性.根据文献[15],将高速公路车流量作为高速公路交通量的量化指标,选取如下11个社会经济指标作为高速公路交通量的经济影响因素:地区生产总值(GDP)、地区固定资产投资总额、地区进出口总额、地区工业生产总值、地区第一产业总产值、地区第二产业总产值、地区第三产业总产值、地区总人口数、地区社会消费品总额、地区货物运输量、地区铁路货物运输量.选取1993—2014年的以上指标数据进行实例计算,相应数据来源于《国家统计局网站》.
4.2 模型训练与预测
将标准化到[0,1]区间的样本数据划分为训练样本集L(1993—2008年数据)和验证样本集Z(2009—2014年数据).ADPSO算法优化LSSVM时,其自身控制参数设定如下:群体规模m设为10;最大迭代步数tmax设为20;惯性权重的最大值δmax、最小值δmin分别设为0.9和0.1.由于ADPSO算法为随机优化算法,每次优化的结果可能在一定范围内产生偏差.为减少ADPSO算法优化偏差对LSSVM参数选择的影响,通过ADPSO算法连续优化LSSVM参数多次,选择最小训练误差对应的参数为最优参数组合(γ*,σ*).根据(γ*,σ*)构建LSSVM并预测2009—2014年的高速公路交通量,再将预测值转化为原始高速公路交通量的预测值.
基于相同数据样本集,分别利用AIWPSO算法优化参数的LSSVM(记作LSSVM-AIWPSO模型)、DACPSO算法优化参数的LSSVM(记作LSSVM-DACPSO模型)预测高速公路交通量.AIWPSO算法优化LSSVM时,其自身控制参数设定如下:群体规模m设为10;最大迭代步数tmax设为20;惯性权重的最大值δmax、最小值δmin分别设为0.9和0.1;加速系数c1、c2均设为2.DACPSO算法优化LSSVM时,其自身控制参数设定如下:群体规模m设为10;最大迭代步数tmax设为20;惯性权重的最大值δmax、最小值δmin分别设为0.9和0.1.将LSSVM-AIWPSO模型和LSSVM-DACPSO模型的预测结果与LSSVM-ADPSO模型进行比较.
4.3 结果分析
选用4种损失函数评价各模型的预测性能:均方根误差(root mean squared error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均百分比误差(mean percentage error,MPE),以及西尔统计量(THEIL),它们分别定义如下:
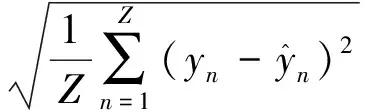
(13)
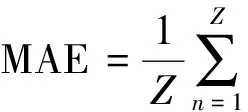
(14)
(15)
(16)
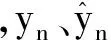
由表1可知,LSSVM-ADPSO模型的预测性能优于LSSVM-AIWPSO模型和LSSVM-DACPSO模型,其最大、最小预测相对误差,以及4个损失函数值均小于LSSVM-AIWPSO模型和LSSVM-DACPSO模型的对应值.这主要是由于ADPSO算法依据适应度值同时更新惯性权重和加速系数的值,显著增强了算法的寻优能力,能正确搜索到LSSVM的全局最优参数,进而提高了LSSVM的预测性能.此外,LSSVM-ADPSO模型2009—2010年的预测相对误差为-3.27%和3.19%,2011—2012年的预测相对误差有所减小,分别为1.08%和0.24%,2013—2014年的预测相对误差又明显增大,分别4.15%和-4.57%,但仍明显高于2009—2010年的预测相对误差,表明LSSVM-ADPSO模型适合于高速公路交通量的短期预测.
通过比较LSSVM-AIWPSO模型和LSSVM-DACPSO模型可知,LSSVM-AIWPSO模型的最大预测相对误差稍大于LSSVM-DACPSO模型的对应值、最小预测相对误差小于LSSVM-AIWPSO模型的对应值;LSSVM-AIWPSO模型的MAE、MPE值小于LSSVM-DACPSO模型的对应值,而RMSE、THEIL值又大于LSSVM-DACPSO模型的对应值.因此,暂时无法确定两模型预测性能的优劣,需进一步研究.
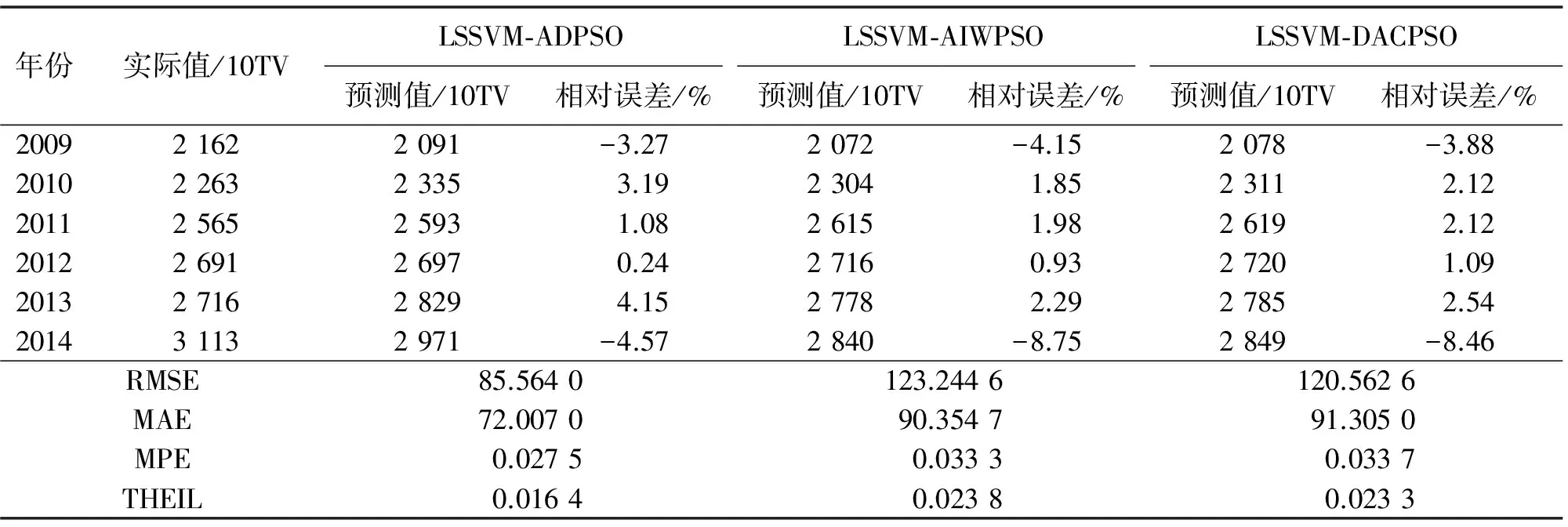
表1 不同模型预测结果比较
10TV代表 10 thousand vehicles.
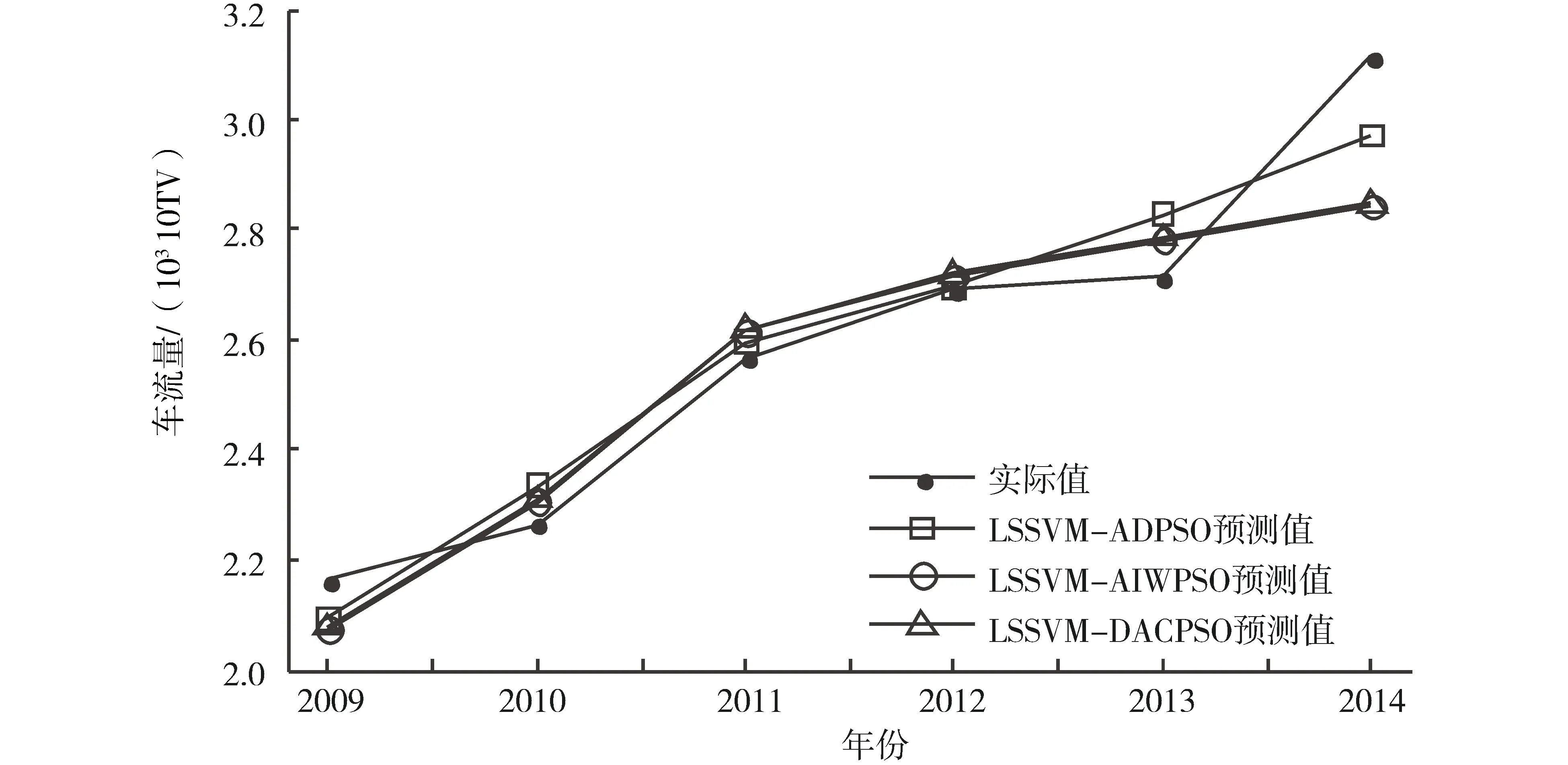
图1 不同模型预测值比较Fig.1 Comparison of forecasting values of different models
由图1可看出,3种模型均较准确地预测出高速公路交通量的逐年增长趋势,在整个预测样本期内,LSSVM-ADPSO模型更好地揭示出高速公路交通量的变化特征,特别是在变化幅度比较大的2012年和2014年,其预测值比其他两模型更接近于实际值;而LSSVM-AIWPSO模型和LSSVM-DACPSO模型2014年的预测值明显偏离实际值.
5 结论
提出高速公路交通量的LSSVM-ADPSO预测模型,LSSVM用于预测高速公路交通量,ADPSO算法用作LSSVM最优参数的选择方法.对某市高速公路交通实例计算表明,LSSVM-ADPSO模型的预测性能优于LSSVM-AIWPSO模型和LSSVM-DACPSO模型,对变化幅度较大的高速公路交通量具有更优的预测效果,适用于高速公路交通量的短期预测.LSSVM-AIWPSO模型与LSSVM-DACPSO模型预测性能的优劣有待进一步研究.
[1] 徐建闽,尹宏宾.广珠高速公路交通量预测[J].系统工程理论与实践,1998,18(4):122-125.DOI:10.3321/j.issn:1000-6788.1998.04.021. XU J M,YIN H B.Guangzhou-Zhuhai expressway traffic volume forecast[J].Systems Engineering-Theory & Practice,1998,18(4):122-125.DOI:10.3321/j.issn:1000-6788.1998.04.021.
[2] 朱顺应,王红,李关寿.路段上短时间区段内交通量预测ARIMA模型[J].重庆交通大学学报(自然科学版),2003,22(1):76-77,95.DOI:10.3969/j.issn.1674-0696.2003.01.019. ZHU S Y,WANG H,LI G S.The ARIMA model used in forecasting of traffic volume in short interval on the link[J].Journal of Chongqing Jiaotong University,2003,22(1):76-77,95.DOI:10.3969/j.issn.1674-0696.2003.01.019.
[3] 高连生,易诞,毛娜,等.基于改进的GM(1,1)的长期交通量预测模型[J].铁道科学与工程学报,2015,12(1):203-207.DOI:10.3969/j.issn.1672-7029.2015.01.033. GAO L S,YI D,MAO N,LI L.A forecast model for long -term traffic volu me based on improved GM(1,1)model[J].Journal of Railway Science and Engineering,2015,12(1):203-207.DOI:10.3969/j.issn.1672-7029.2015.01.033.
[4] 王炎,王华.基于BP-NN和遗传算法的高速公路交通量预测[J].计算机工程与应用,2006(4):226-228.DOI:10.3321/j.issn:1002-8331.2006.04.070. WANG Y,WANG H.Prediction of highway traffic based on BP-neural network and genetic algorithms[J].Computer Engineering and Applications,2006(4):226-228.DOI:10.3321/j.issn:1002-8331.2006.04.070.
[5] VAPNIK V N.An overview of statistical learning theory[J].IEEE Transactions on Neural Networks,1999,l0(5):988-999.DOI:10.1109/72.788640.
[6] HU W B,YAN L P,LIU K Z,et al.A Short-term traffic flow forecasting method based on the hybrid PSO-SVR[J].Neural Processing Letters,2016,43(1):155-172.DOI:10.1007/s11063-015-9409-6.
[7] AHN J,KO E,KIM E Y.Highway traffic flow prediction using support vector regression and Bayesian classifier[Z].The IEEE International Conference on Big Data and Smart Computing (BigComp),HongKong,2016.DOI:10.1109/BIGCOMP.2016.7425919.
[8] SUYKENS J A K,VANDEVALLE J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.DOI:10.1023/A:1018628609742.
[9] 戢小辉.基于灰色关联的LS-SVM道路交通事故预测[J].计算机应用研究,2016,33(3):806-809.DOI:10.3969/j.issn.1001-3695.2016.03.037. JI X H.Forecast model of road traffic accidents based on LS-SVMwith grey correlation analysis[J].Application Research of Computers,2016,33(3):806-809.DOI:10.3969/j.issn.1001-3695.2016.03.037.
[10] 邓佳佳,刘爽.基于免疫模糊聚类的LSSVM在短期负荷预测中的应用[J].河北大学学报(自然科学版),2012,32(3):234-239.DOI:10.3969/j.issn.1000-1565.2012.03.003. DENG J J,LIU S.Application of LSSVM based on immune fuzzy clustering algorithm to short-term load forecasting[J].Journal of Hebei University(Natural Science Edition),2012,32(3):234-239.DOI:10.3969/j.issn.1000-1565.2012.03.003.
[11] POLI R,KENNEDY J,BLACKWELL T.Particle swarm optimization:An overview[J].Swarm Intelligence,2007,1(1):33-57.DOI:10.1007/s11721-007-0002-0.
[12] SHI Y,EBERHART R C.Empirical study of particle swarm optimization[Z].The IEEE International Congress on Evolutionary Computation,Piscataway,NJ,USA,1999.DOI:10.1109/CEC.1999.785511.
[13] 纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009.
[14] 姜长弘,张永恒,王盛慧.基于自适应粒子群算法的篦冷机电液位置饲服系统PID参数优化[J].液压与气动,2016(7):44-49.DOI:10.11832/j.issn.1000-4858.2016.07.009. JIANG C H,ZHANG Y H,WANG S H.PID parameter optimization of the gate cooling electro-hydraulic position servo system based on adaptive particle swarm optimization algorithm[J].Chinese Hydraulics & Pneumatics,2016(7):44-49.DOI:10.11832/j.issn.1000-4858.2016.07.009.
[15] 赵泽辉.高速公路交通量预测及山区高速公路后评价研究[D].大连:大连理工大学,2015. ZHAO Z H.Highway traffic forecasting and post-evaluation research of mountain highway[D].Dalian:Dalian University of Technology,2015.
(责任编辑:孟素兰)
A forecasting method of highway traffic flow using LSSVM optimized by ADPSO algorithm
SI Wenjing1,FENG Xibo2,GENG Liyan3,4,ZHANG Zhanfu5
(1.Construction Engineering Department,North China Institute of Aerospace Engineering,Langfang 065000,China;2.Hebei Province Expressway Langfang Beisanxian County Management Department,Langfang 065000,China;3.School of Economics and Management,Shijiazhuang Tiedao University,Shijiazhuang 050043,China;4.Business School,Manchester Metropolitan University,Manchester,M15 6BH,UK;5.Sifang College,Shijiazhuang Tiedao University,Shijiazhuang 051132,China)
There is a complex nonlinear relationship between highway traffic flow and its influencing factors.Combing least squares support vector machines (LSSVM) with adaptive dynamic particle swarm optimization (ADPSO) algorithm,this paper proposed a new highway traffic flow forecasting method based on LSSVM optimized by ADPSO algorithm.Highway traffic flow was forecasted by LSSVM with the advantages of easy modeling and high precision.And the optimal parameters of LSSVM were selected based on the good optimization ability of ADPSO algorithm.An example analysis on the highway traffic flow in a city was performed to test the effectiveness of LSSVM-ADPSO model.The results indicate that the proposed method has better highway traffic flow forecasting performance and is suitable for short-term highway traffic flow forecasting.
highway;traffic flow forecasting;adaptive dynamic particle swarm optimization algorithm;least squares support vector machines
2016-12-25
国家自然科学基金青年项目(61503261);河北省交通运输厅科技计划项目(Y-2010024);北华航天工业学院科研基金项目(KY-2015-09); 河北省软科学研究计划项目(15456106D);河北省高等学校青年拔尖人才计划项目(BJ2014097);河北省社会科学发展重点课题(2015020206);国家留学基金委(CSC)公派留学地方合作项目(201608130165);河北省高校人文社会科学重点研究基地石家庄铁道大学工程建设管理研究中心资助项目;河北省软科学工程建设管理研究基地资助项目;河北省重点学科管理科学与工程资助项目
司文静(1980—),女,河北迁安人,北华航天工业学院讲师,主要从事道路与桥梁工程方面的研究. E-mail:siwenjing1021@sina.com
封喜波(1979—),男,河北平山人,河北省高速公路廊坊北三县管理处高级工程师,主要从事交通工程方面的研究. E-mail:6511129@qq.com
10.3969/j.issn.1000-1565.2017.03.013
U491.14
A
1000-1565(2017)03-0302-07

