高考知识专题：数列与数学归纳法*

●严兴光 李绍塔

(杭州第十四中学 浙江杭州 310000)

高考知识专题：数列与数学归纳法*

●严兴光 李绍塔

(杭州第十四中学 浙江杭州 310000)

数列是近几年浙江省数学高考的重点也是难点之一.文章从近几年高考卷对数列的考查情况入手，由浅入深分析高考中数列题所考查的内容、常用的解题方法、压轴题的出题方向、解压轴题常用的数学思想方法以及如何突破数列压轴题等.

数列；数学归纳法；不等式

1 知识内容

数列部分主要内容有：等差(等比)数列,数列求通项的基本方法，数列求和的基本方法，比如叠加法、叠乘法、倒序相加法、错位相减法、裂项法等，以及不等式与数列的综合问题和利用数学归纳法证明数列问题等．

2 命题分析

从考查形式看，在历年的浙江省数学高考中，数列问题一般以1个小题(填空题或选择题)和1道解答题的形式出现.作为考查考生创新意识与实践精神的最好素材，一些构思精巧、新颖别致、极富思考性和挑战性的数列与方程、函数、不等式等的综合性试题不断涌现，这部分试题往往以压轴题的形式出现，考查综合运用知识的能力，突出知识的融会贯通．

从考查内容看，小题主要以等差数列和等比数列为载体，考查数列的概念、表示法、求通项、求和等；综合题常与不等式、函数的最值、归纳猜想、分类讨论等数学思想相结合，技巧性比较强，需要平时一定量的训练与积累，在后续复习时应予以关注．

3 典题剖析

考点1 数列求通项问题

与通项公式有关的问题是前几年浙江省数学高考数列小题考查的重点内容，主要知识点有：等差(等比)数列通项公式、一些简单的可以转换为等差数列或等比数列的递推式以及周期数列等．

例1 设等比数列{an}满足a1+a3=10，a2+a4=5，则a1a2…an的最大值为______.

于是当n=3或n=4时，a1a2…an取到最大值26=64．

例2 设数列{an}的前n项和为Sn，数列{Sn}的前n项和为Tn，满足Tn=2Sn-n2，其中n∈N*.

1)求a1的值；

2)求数列{an}的通项公式．

考点2 数列求和问题

数列求和的常用方法有公式法(等差数列和等比数列)、倒序相加法、错位相减法、裂项相消法、分组转化求和法、并项求和法，在解题过程中要合理选择求和公式．

1)求数列{an}，{bn}的通项公式；

评注 利用裂项相消法求和时，应注意：1)抵消后并不一定只剩下第1项和最后1项，也有可能前面剩2项，后面也剩2项；2)将通项公式裂项后，有时候需要调整前面的系数，使裂开的2项之差和系数之积与原通项公式相等．

考点3 数列综合问题

数列解答题一般具有很强的综合性，考查的知识以等差、等比数列的性质为主，兼顾其他知识．

数学归纳法是一种证明与正整数n有关的数学命题的重要方法．

1)证明：an+1>an；

证法2 用数学归纳法证明an+1>an>2.

由归纳假设可得ak+2>ak+1>2 成立.

综上所述，an+1>an成立.

进而

由

知

评注 裂项求和是求解本题的关键.由于本题涉及的裂项方法不常规，复习过程中特别要引起重视.类似的问题还有2015年浙江省高中数学竞赛试题第6题：

( )

分析 由题意

即

(x+1)(2x+1)…(2 015x+1)>0，

于是

考点4 数列与不等式综合问题

数列是特殊的函数，不等式是深刻认识函数与数列的重要工具，2者的综合是近几年高考命题的新热点，且数列的重心已经偏移到不等式的证明与求解中，而不再是以前的递推求通项．

例6 已知数列{an}满足a1=1，an+1=3an+1.

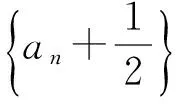
3n-1≥2·3n-1，

从而

于是

故

评注 对于数列问题中求和类不等式的证明，若是通过放缩的方法进行证明的，则一般有2种类型：1)能够直接求和(或求积)，再放缩；2)不能直接求和(或求积)，需要放缩后才能求和(或求积)，求和(或求积)后再进行放缩(比如本题)，一定要注意“缩的尺度”和“从哪一项开始放缩”．

1)证明：|an|≥2n-1(|a1|-2),n∈N*；

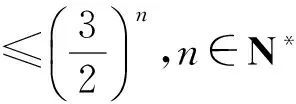
本题作为浙江卷2016年高考试题，体现浙江高考试题入口宽、方法多、结构精巧、简约而不简单的特点．

即

对右边的不等式2边同除以2n,得

从而当n≥2,n∈N*时，

故

|an|≥2n-1(|a1|-2),

另外，当n=1时，显然成立.综上，|an|≥2n-1(|a1|-2),n∈N*.

因此，将这些知识和方法迁移至本题的证明如下：

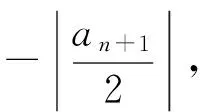
|an+1|+2≤2(|an|+2)，

从而

|an|+2≤2n-1(|a1|+2)，

即 |an|≤2n-1(|a1|+2)-2,

(1)

|an+1|-2≥2(|an|-2)，

若|an|>2，则易得

|an|-2≥2n-1(|a1|-2),

即 |an|≥2n-1(|a1|-2)+2,

(2)

如果(2)式成立，那么第(1)问所证结论|an|≥2n-1(|a1|-2)成立.

这里，为得到(2)式，添加|an|>2这个条件，下面来说明这个条件的合理性.

①当|a1|≤2时，则|an|≥0≥2n-1(|a1|-2)显然成立；

②当|a1|>2时，则由|an+1|-2≥2(|an|-2)，再结合数学归纳法的思想，易得|an|>2，从而|an|≥2n-1(|a1|-2)+2>2n-1(|a1|-2)成立．

2)证法1 延续第(1)问证法1的思想，则任意n，m∈N*,m>n,有

故

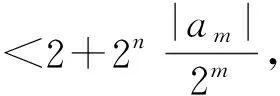
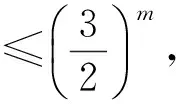
再由m的任意性可得|an|≤2,n∈N*，理由如下：

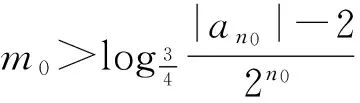
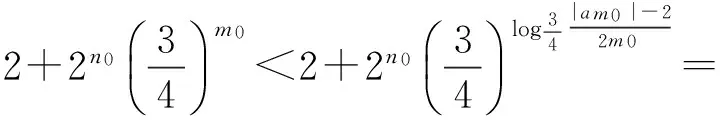
综上，任意n∈N*,|an|≤2.

假设任意n∈N*,|an|≤2不成立，即存在k∈N*,|ak|>2成立.则由第(1)问证法2同理可得

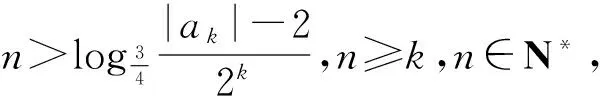
即

因此，假设不成立，从而任意n∈N*,|an|≤2.

评析 第1)小题所证的式子|an|≥2n-1(|a1|-2)中已经在提示考生，需要进行|an|-2的代数变形，然后放缩出一个等比数列，这也正是浙江省高考一直以来的特点，难题总是会留下一些线索，让考生“有机可乘”．

m·2n≤2n-1(|a1|-2)+2≤|an|≤2n-1(|a1|+2)-2≤M·2n(其中m>0,M>0).

4 精题集萃

1．已知等差数列{an}前9项的和为27，a10=8，则a100=

( )

A.100 B.99 C.98 D.97

2．设{an}是等差数列，下列结论中正确的是

( )

A．若a1+a2>0，则a2+a3>0 B．若a1+a3<0，则a1+a2<0

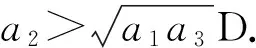
3．已知{an}为等差数列，Sn为其前n项和，若a1=6，a3+a5=0，则S6=______.

4．设Sn是数列{an}的前n项和，且a1=-1，an+1=SnSn+1，则Sn=______．

5．无穷数列{an}由k个不同的数组成，Sn为{an}的前n项和.若对任意n∈N*，Sn∈{2,3}，则k的最大值为______.

7．设等差数列{an}的公差为d，前n项和为Sn，等比数列{bn}的公比为q．已知b1=a1，b2=2，q=d，S10=100．

1)求数列{an}，{bn}的通项公式；

图1

参 考 答 案

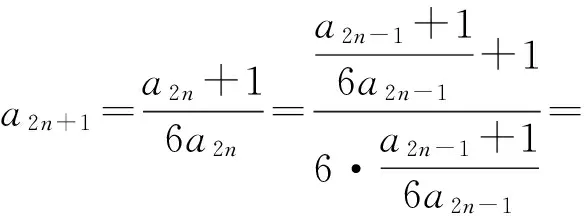
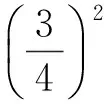
2017-01-04；

2017-02-23

严兴光(1975-)，男，浙江杭州人，中学高级教师.研究方向：数学教育、技术与数学课程整合研究.

O122

A

1003-6407(2017)04-29-05