从解析法到几何直观*
——从几道与圆有关的试题谈圆的几何直观
●李守明
(舟曲中学 甘肃兰州 730087)
从解析法到几何直观*
——从几道与圆有关的试题谈圆的几何直观
●李守明
(舟曲中学 甘肃兰州 730087)
圆具有许多直观的几何性质,在高中解析几何中若能合理运用这些性质,则能够理解与圆有关的解析几何试题产生的几何背景,并且简化解析几何的运算.文章从一道高三复习试题入手,结合高考试题,阐述了圆的直观几何性质在解题中的意义.
圆;解析法;几何直观
在高三解析几何有关圆的章节复习中,遇到这样一个试题:

图1
例1 如图1所示,⊙C是坐标平面上通过点M(0,-2),N(6,4)的圆,若⊙C与x轴交于点A,B,求线段AB长的最小值.
遇到一个数学问题,首先想到解题切入点与思路是什么?其次想到的是有没有简便易行的方法?带着这样2个想法,笔者走进了解题之旅.
1 解题的切入点及思路
这道题是求⊙C与x轴相交的弦AB长的最小值,是一道求最值的问题.只有变化的量才能引起最值,一般应该建立起弦AB的长与某个变量的函数关系,借助求函数值域的方法来解决,故本题的关键是如何表示出弦AB的长.从解析几何中如何求直线与圆相交弦长入手,因此有了如下思路:
思路1 在⊙C中,借助垂径定理,构造直角三角形来求弦长.
解法1 设⊙C的标准方程为
(x-a)2+(y-b)2=r2,
则
又M(0,-2),N(6,4)在⊙C上,从而
消去r2,得到
a+b=4,
因此AB2= 4(r2-b2)=
4[(6-a)2+(4-b)2-b2]=
4[(6-a)2+a2-(4-a)2]=
4[(a-2)2+16]≥64,
当a=2时,取到等号,故线段AB长的最小值为8.
思路2 线段AB是x轴与⊙C的交点弦,故可以通过弦长公式来表示弦长.
解法2 设⊙C的一般方程为
x2+y2+dx+ey+f=0,
由M(0,-2),N(6,4)在⊙C上,得

消去d和f,得到
x2+y2-(8+e)x+ey+2e-4=0.
设A(x1,0),B(x2,0),则
x1+x2=8+e,x1x2=2e-4,
从而AB2= |x1-x2|2=(x1+x2)2-4x1x2=
(e+4)2+64≥64,
当e=-4时,取到等号,满足d2+e2-4f>0,故线段AB长的最小值为8.
思路3 线段AB所在直线为x轴,经过定点P,倾斜角为0°,故可以设出直线的参数方程,利用参数的几何意义表示线段AB的弦长.
解法3 根据思路2,⊙C的方程为
x2+y2-(8+e)x+ey+2e-4=0.
又依据两点式可求出直线MN的方程为
x-y-2=0,
令y=0,则x=2,故P(2,0),直线AB的参数方程为

代入x2+y2-(8+e)x+ey+2e-4=0,得
t2-(4+e)t-16=0.
设点A,B对应的参数分别为t1,t2,则
AB2= |t1-t2|2=(t1+t2)2-4t1t2=
(e+4)2+64≥64,
当e=-4时,取到等号,满足d2+e2-4f>0,故线段AB长的最小值为8.
评注 解题方法的不同是因为解题思路的不同,这3种思路建立弦长AB与某个变量关系的角度虽然不同,其实本质是相同的,都是把弦长AB作为函数,分别建立了与变量a(思路1)和变量e(思路2和思路3)的函数关系,最后借助求二次函数值域的方法得到弦长AB的最小值.思路自然亲切,操作性强,学生易于掌握.
解析几何是用代数的方法研究几何问题,解析几何求最值的试题中,若题目的条件和结论能体现一种明确的函数关系,则优先考虑建立起目标函数,然后求这个函数的最值,常用配方法、基本不等式法及导数法等求解.
此题能否从⊙C的几何性质入手,借助几何直观来解决这个问题呢?
2 解题的简便方法:几何直观
思路4 由于⊙C只是经过点M,N的圆,并不是固定的,⊙C的变化引起了与x轴相交弦AB的变化,但这个弦有个特点:经过定点P.另外,静止和运动是相对的,我们可以固定⊙C,让x轴变化,那么这个问题就转化为经过圆内一定点P的弦长的最小值是多少的问题了,从而有了下面的解法:
解法4 经过⊙C内定点P的弦AB与CP垂直时弦长最短.此时圆心C在直线x=2与MN垂直平分线的交点处.
MN垂直平分线的方程为x+y-4=0,令x=2,代入x+y-4=0,则y=2,从而C(2,2),于是
r2=CN2=20.
⊙C的方程为 (x-2)2+(y-2)2=20,
令y=0,x1=-2,x2=6,则
AB=|x1-x2|=8,
故线段AB长的最小值为8.
思路5AB与MN是圆内经过定点P的2条相交弦,可以充分利用初中学过的平面几何知识,利用相交弦定理来解决.

从而
PA·PB=PM·PN=16,
根据基本不等式
当PA=PB=4时,取到等号.
评注 思路4需要明确经过圆内一点的弦在哪种情况下取得最小值这个条件,这就要求平时的积累和总结;思路5发挥了圆自身的几何性质,相交弦定理对高中学生来说,是圆的一种很直观的性质,与基本不等式相结合,简化了解题的程序,确有神来之笔的一种感觉.思路4和思路5都是圆的几何直观在解析几何解题中体现出来的,几何直观在解析几何解题中的显著作用是解析法不可替代的.
3 圆的几何直观的意义
3.1 借助圆的几何直观,理解试题的产生背景

( )
(2016年四川省数学高考理科试题第10题)


因此点D既是△ABC的外心又是垂心,从而△ABC为等边三角形.又

故



图2

x2+(y-3)2=1.

进而

故选B.
思路2 (向量法)如图2,取AC的中点为E,则
于是

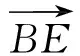

图3

评注 比较以上3种思路,思路3不仅解题方法简洁,更能反映试题产生的背景:圆外一点与圆上点确定线段长度的最值问题.
3.2 借助圆的几何直观,简化解析几何运算解析几何的解题过程中,几何条件的转化对解题的难易起着决定作用,引导学生从图形入手,挖掘几何图形隐藏的条件,利用几何直观解题显得非常简单.
例2 如图3,在平面直角坐标系xOy中,已知以M为圆心的⊙M:x2+y2-12x-14y+60=0及其上一点A(2,4).
1)设⊙N与x轴相切,与⊙M外切,且圆心N在直线x=6上,求⊙N的标准方程;
2)设平行于OA的直线l与⊙M相交于点B,C,且BC=OA,求直线l的方程;

(2016年江苏省数学高考试题第18题)
1)(x-6)2+(y-1)2=1;
2)l:y=2x+5或y=2x-15.
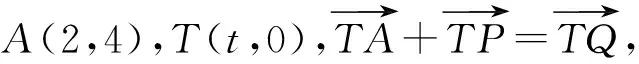

(1)
(1)又因为点Q在⊙M上,所以
将式(1)代入式(2),得
(x1-t-4)2+(y1-3)2=25




从而

解得


评注 本题第3)小题的解法1从2个圆有公共点这个条件入手,2个圆的圆心距满足关系|R-r|≤d≤R+r,建立了关于t的不等式,思路清楚但略显繁琐;而解法2充分利用已知条件,从简单的几何直观可以知道圆上任意2个点的距离不超过直径的长度这一事实,以此为依据建立关于t的不等式,大大地减少了解析几何的运算量,令人耳目一新!
4 结束语
我国数学教育家徐利治曾说过:“直观就是借助于经验、观察、测试或类比联想,所产生的对事物关系直接的感知与认识,而几何直观是借助于见到的或想到的几何图形的形象关系产生对数量关系的直接感知.”熟悉几何图形的性质是几何直观感知的源泉,但并不是每道题都有明显的几何直观,在教学中,教师有意识地培养学生的几何直观能力,对提高学生思维的深刻性和灵活性一定是大有裨益的.
2016-12-26;
2017-02-20
李守明(1974-),男,甘肃秦安人,中学一级教师.研究方向:数学教育.
O123.1
A
1003-6407(2017)04-11-03

