高中数学平面向量问题解法探究*

●汪道智

(富阳新登中学 浙江杭州 311404)

高中数学平面向量问题解法探究*

●汪道智

(富阳新登中学 浙江杭州 311404)

平面向量问题在高考卷及各种模拟卷、竞赛卷中常有涉及.教学过程中发现学生碰到向量问题时要么不知道应该怎样入手，要么解法单一.文章试图将平面向量问题的解法做一个归纳整理，教会学生该如何解决平面向量问题.

平面向量;数形结合;极化恒等式

近年来，高中数学的平面向量问题在高考卷以及各地高考模拟试卷中常有涉及，且其解题方法多种多样.平面向量兼具代数和几何特性，是沟通代数与几何的一种工具，是数学中数形结合思想的典型体现.笔者作为一线教师，对近年来各地区平面向量的高考题以及各地模拟题的类型进行了归纳整理，下面将对平面向量问题的解题方法进行总结与探究，希望能对学生的学习有所帮助.

1 将向量问题转化为函数问题，以数助形

1.1 坐标法

在教学中,经常提及的平面向量的解决方法是通过建系引入坐标，将向量的运算转化为代数运算，这样就可以将“形”与“数”紧密结合.建立直角坐标系是平面向量代数化最直接的方法.

例1 已知a,b是单位向量，a·b=0.若向量c满足|c-a-b|=1，则|c|的取值范围是

( )

(2013年湖南省数学高考理科试题第6题)

图1

分析 由于a,b是相互垂直的单位向量，故可建立直角坐标系，运用向量的坐标运算来求解.

c-a-b=(x-1,y-1),

又|c-a-b|=1，从而

(x-1)2+(y-1)2=1，

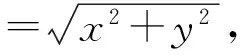
1.2 利用三角函数来解决向量问题

若建系后条件中出现变量在某个圆上运动时，可以引入三角函数来处理相关问题.

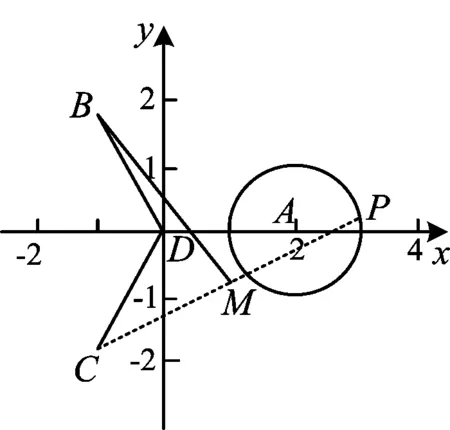
图2

(2016年四川省数学高考理科试题第10题)

分析 本题中有动点与定点，首先要根据条件找到动点的轨迹，再用三角函数去解决.

x0=2+cosθ，y0=sinθ.

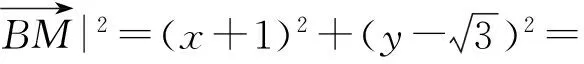
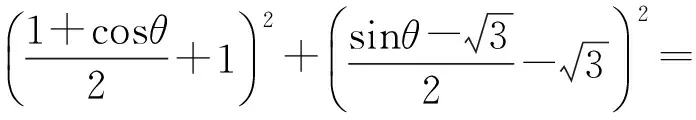
2 运用平面向量几何特性，以形助数

(2016年江苏省数学高考试题第13题)

图3

分析 用基底表示其他向量是解答本题的关键.

9b2-a2=4,

b2-a2=-1,

2.2 平面向量数量积的几何意义平面向量数量积定义是a·b=|a|·|b|cosθ，其几何意义是一向量的模与它在另一向量方向上的投影的乘积.数量积的几何意义能帮助学生理解向量作为工具的真正内涵，恰当运用数量积的几何意义能很大程度地减少运算量[1].

(2012年湖南省数学高考文科试题第15题)

图4

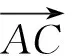
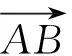
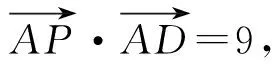
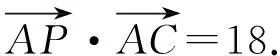
3 图形构造

向量加法、减法等运算特有的几何意义使得数形结合这一重要的数学思想在解题中发挥着重要的作用.2015年与2016年浙江省数学竞赛中的平面向量问题都是通过构造图形再利用图形特征求解的.

(2015年浙江省高中数学竞赛试题第14题)

分析 由本题条件可以考虑建系，用坐标运算解题，但变量较多，计算量相对较大.而按照题目要求直接构造图形，可化繁为简.

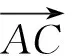
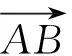
AC2=|a|2+|c|2-|a|·|c|cos∠AOC,即

|a|·|c|≤30，于是

a·c=|a|·|c|cos∠AOC≤24

即a·c的最大值为24

图5 图6

(2016年浙江省高中数学竞赛试题第6题)

由图可知 ED+DC≥EC=26.

故选B.

4 实现平面向量代数化的主要工具

几何意义:平行四边形对角线的平方和等于4条边的平方和.

( )

A.min{|a+b|,|a-b|}≤min{|a|,|b|}

B.min{|a+b|,|a-b|}≥min{|a|,|b|}

C.max{|a+b|2,|a-b|2}≤|a|2+|b|2

D.max{|a+b|2,|a-b|2}≥|a|2+|b|2

(2014年浙江省数学高考理科试题第8题)

解 根据向量运算的三角形法则知，min{|a+b|2,|a-b|2}与min{|a|,|b|}大小不定，排除选项A,B.由上述等式，即

|a+b|2+|a-b|2=2|a|2+2|b|2，可得

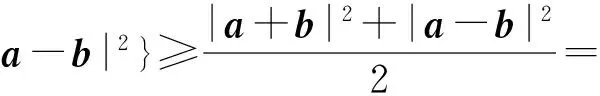
|a|2+|b|2.

故选D.

图7 图8

工具2 极化恒等式：

下面举例说明极化恒等式的妙用：

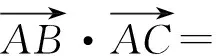
(2012年浙江省数学高考理科试题第15题)

分析 本题是使用极化恒等式解题的典型例题.

(2013年浙江省数学高考理科试题第7题)

A.∠ABC=90° B.∠BAC=90°C.AB=ACD.AC=BC

图9

分析 此题可以考虑建系，运用坐标运算转化成函数问题来处理.但是变量较多，对学生的化归能力以及计算能力要求较高.本题运用极化恒等式处理非常简洁明了.

解 如图9，在△PBC中，由极化恒等式得

在△P0BC中,有

因此对于边AB上任一点P，恒有

从而

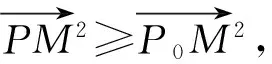
即MP0⊥AB.

工具3 三角形不等式：|a|-|b|≤|a±b|≤|a|+|b|.

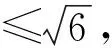
(2016年浙江省数学高考理科试题第15题)

分析 本题将上述实现平面向量问题代数化的几个工具用到了极致.

解 由三角形不等式得

由单位向量e的任意性可得

从而

10=2(a2+b2)=(a+b)2+(a-b)2，

于是

(a-b)2≥4.

综观近年来的数学高考试卷，平面向量的题型越来越灵活多变.在平常教学中经常听到教师对学生说：“向量问题能建系则建系.”这是对学生的一种误导,容易造成学生碰到难以建系的向量问题而无从下手,教师应引导学生根据题中不同的条件选择相应的解题方法.如文中提及的基底法、图形构造、数量积几何意义、极化恒等式、三角形不等式等，都是解决平面向量问题的基本方法.总之，平面向量问题灵活多变，笔者不可能将所有方法一一列举，以上只是平时向量教学中的一些解题方法小结，意在教学中加强学生对解题工具的选择能力，加深学生对数学本质的理解.

[1] 王苏文.巧用数量积的几何意义[J].中学生数学，2013(4)：16-17.

[2] 王红权.巧用极化恒等式 妙解一类向量题[J].中学教研(数学)，2013(8)：24-25.

2016-12-21；

2017-02-16

汪道智(1980-)，男，浙江杭州人，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)04-14-04